基于多代理模型的离心叶轮高效优化设计方法

刘基盛　计良　李威　贾志新　成金鑫　方鹏程

摘要：针对自动优化设计时迭代过多、耗时过长等问题，建立了基于多代理模型优化算法的离心压气机叶片高效寻优模型，研究了全局/局部模型管理策略和样本填充方法，对比分析了多代理模型与常用的元启发式优化算法（粒子群算法、多岛遗传算法等）的综合性能，验证了多代理寻优模型的高效性。离心叶轮优化结果表明：等熵效率提高了0.73%，总压比增大了0.18%，喘振裕度提高了1.1%；与经典粒子群算法相比，优化时间缩短54.9%。

关键词：离心叶轮；叶片几何外形；高效寻优；优化算法；多代理模型

中图分类号：TH122

DOI：10.3969/j.issn.1004-132X.2023.08.003

Efficient Optimization Design Method of Centrifugal Impellers Based on Multi-surrogate Model

LIU Jisheng1 JI Liang2 LI Wei1 JIA Zhixin1 CHENG Jinxin1 FANG Pengcheng3

Abstract： Aiming at the problems of excessive number of iterations and time consumption in automatic optimization design， an efficient optimization search model for centrifugal compressor blades was established based on multi-surrogate model optimization algorithm. A global/local model management strategy and a sample filling method were studied. The comprehensive performance of multi-surrogate model and common meta-heuristic optimization algorithms（particle swarm algorithm， multi-island genetic algorithm， etc. ）were compared and analyzed， and the effectiveness of the efficient optimization search model was verified. The results of the centrifugal impeller optimization show that the isentropic efficiency is improved by 0.73%， the total pressure ratio is increased by 0.18%， and the surge margin is improved by 1.1%. Compared with the classical particle swarm algorithm， the optimization time may be reduced by 54.9%.

Key words： centrifugal impeller； blade geometry shape； efficient optimization seeking； optimization algorithm； multi-surrogate model

0 引言

離心压气机叶轮在工作时呈现大逆压梯度和强三维效应等特征，这使得内部气体流动较为复杂，容易造成能量损失。叶片几何外形气动优化设计方法是实现叶轮机械高负荷高性能的重要技术手段，因此优化算法是叶轮机械优化设计领域研究的主要方向。

元启发优化算法（粒子群算法、进化算法等）［1-4］模仿自然界和人类社会领域中的相关行为、经验和规则，采用迭代搜索方式求解复杂优化问题，具有能跳出局部“陷阱”、获取全局最优解的优势，是目前叶轮机械优化中研究和应用最为广泛的智能算法。BASHIRI等［5］利用粒子群优化算法（PSO）和计算流体动力学（CFD）对离心叶轮几何外形进行优化，使其效率提高了3.2%。孔庆国等［6］基于PSO算法和中弧线曲率控制方法对压气机叶片进行了优化设计，优化后的设计点总压损失显著降低。元启发算法在实际应用工程的优化中需遍历整个寻优空间，每次的数值模拟计算通常需要几分钟甚至几小时，寻优迭代至少需要上千次（昂贵计算），整个优化流程耗时数十天甚至更长。刘基盛等［7］利用遗传算法对离心压气机进行了全叶片优化设计，虽然气动性能改善明显，但是迭代寻优需要1200次，计算时间需要30天，评估耗时较长。

近年来，为减少中高维（大于20维）自动优化设计时的迭代，提高寻优效率，计算机领域发展了多代理模型优化理论，将计算时间成本低廉的机器学习模型代替昂贵的模拟评估成为智能计算领域研究的热点。集成多个具有不同特性的单一代理模型，可构建出普适性更强、近似精度更高的多代理模型［8-11］。因此，研究基于多代理模型算法的叶片优化设计方法对解决实际工程中的“高耗时评估问题”具有积极意义。

1 优化设计方法

如图1所示，叶轮机械自动优化设计流程如下：①对原始叶片几何构型布局设计变量，并将设计变量进行参数化表达；②利用参数化建模方法生成新的叶轮几何外形；③利用仿真软件对新叶轮进行网格划分和流场计算；④对新叶轮进行气动性能评估，若满足循环迭代条件则利用优化算法更新设计参数，若不满足迭代条件则退出循环程序，得到最佳叶轮；⑤重复步骤②～④。参数化建模和算法优化是叶轮自动优化设计过程中最重要的两个环节。

1.1 参数化建模方法

传统离心叶轮参数化方法存在设计变量多、构型灵活度差、叶型型线缺乏径向约束等问题，因此本文采用双Bezier曲面参数化方法［7］，即通过扰动Bezier曲面来控制叶片型面的形状（Bezier曲面叠加的扰动量为0时，叶片生成面就是原始叶片型面）。该方法利用优化变量在一维方向上的变化，可以实现三维叶片吸力面和压力面的自由变形，有效减少了设计变量，并具有构型灵活、径向约束和高阶连续性等优势。

1.2 多代理模型优化算法

代理模型的选取是建模技术的核心，不同的优化问题需要匹配不同的近似模型，但无法预知哪种代理模型可以精确逼近真实模型，将精度较高的几种代理模型进行加权组合可以解决选型问题，并能有效降低计算成本。常用的组分模型有多项式响应（polynomial response，PR）模型、Kriging模型和径向基函数（radial basis function，RBF）模型［12］。

多代理模型优化算法（multi-surrogate model optimization algorithm，MMOA）借鉴模型管理方法［13］，其流程如图2所示，图中，桔色框表示全局模型管理策略，綠色框表示局部模型管理策略，桔色箭头表示利用全局策略得到的适应度评估值并进行样本填充，绿色箭头表示利用局部策略得到的适应度评估值并进行样本填充。

（1）采用拉丁超立方采样方法初始化5d（d为变量的维数）个样本。对初始样本的每个个体进行数值模拟计算得到适应评估值；基于初始样本和计算结果构建全局多代理模型（multiple surrogate models，MSM）：

式中，y^MSM（x）为MSM的预测响应值；n为代理模型的总数；x为d维决策向量；y^i（x）为第i个单一代理模型的预测响应值；wi为第i个单一代理模型的权重；Eavg为n个模型的平均预测平方和；常数α、β为调整参数，推荐取α=0.05和β=-1；Ei为第i个代理模型的预测平方和；p为样本数据总数；e^q为去除第q个数据后，剩余的p-1个数据构建出代理模型后对第q个数据进行预测的误差平方和；yq－y^q为预测偏差；yq为第q个数据的实际值；y^q为代理模型对第q个数据的预测值。

其中，yUM（x）是在预测解x处组分模型之间的不确定度，即不同的两个组分成员输出的最大差值；训练数据集Sk={（x1，y1），（x2，y2），…，（xk，yk）}的每组数据包括决策变量和计算得到的适应度评估值。若不确定性最大解为（xUMk+1，yUMk+1），则被添加到样本数据集合Sk中，并 重新更新MSM。

（3）求解更新后MSM的全局最优解：

并对其进行昂贵计算，获得yGk+2，将（xGk+2，yGk+2）添加到数据集Sk+1并更新MSM。

（4）重复步骤（3），当MSM不能进一步改进时，将所有优于初始样本的数据添加到数据集SL，有利于求出局部最优解，并建立一个基于少量数据集SL的多代理模型MSM_L，并求解y^MSM_L的预测最优解：

对预测最优解xL进行昂贵计算，得到适应度yL，将（xL，yL）添加到数据集S和SL，更新MSM和MSM_L。

（5）当局部模型管理不能进一步改进时，循环执行步骤（2）～（5），直到总迭代次数达到11d。

为验证MMOA昂贵计算问题中的优化效果，将其与多岛遗传算法（MIGA）、粒子群（PSO）算法和差分进化（DE）算法在测试函数上进行对比。算法MMOA、MIGA、PSO和DE均执行30次独立重复性实验，测试维度分别设为20、30、40，如表1所示。

以MMOA迭代11d次的运算结果作为基准值，记录其他算法收敛到基准值时的迭代次数，实验数据如表2～表4所示。由测试数据可知，中高维求解问题中，MMOA在评估次数上具有明显优势，虽然耗时较多，但对于实际工程问题中动辄需数十天的模拟仿真计算，多出的运行时间可基本忽略，所以采用MMOA可以减少昂贵计算的迭代，大幅提高计算效率，改善求解质量。

2 离心叶轮气动优化设计研究

2.1 优化对象

结合双Bezier曲面参数化方法、MMOA及CFD技术，构建了额定工况下的离心压气机叶片高效优化设计模型。研究对象为额定输出功率100 kW、峰值转速可达100 000 r/min的离心压气机叶轮，优化对象为主叶片和分流叶片的几何外形，端壁面形状在优化过程中保持不变。叶轮模型见图3，气动参数和几何参数如表5所示。

2.2 优化目标与约束条件

选取额定工况近峰值效率点为优化工况点，在额定工况下通过寻优叶片最佳几何外形，使离

心压气机叶轮的等熵效率最大化，以叶片映射的单位Bezier曲面控制顶点为设计变量［7］，以总压比不降低作为约束条件，目标函数和约束条件如下：

式中，ηROC为原始叶轮额定工况的等熵效率；xi为优化控制变量，其上下限分别为xUi和xLi；πROC_opt、πROC_ori分别为叶轮的原始总压比和优化后总压比。

目标函数和设计变量是隐形关系（“黑箱”问题）。“黑箱”问题的求解可采用随机迭代优化算法，即只关注输入值和输出值，摆脱了中高维复杂优化设计问题对人为经验的依赖。

2.3 数值计算方法

数值模拟技术已广泛用于研究叶轮机械的内部流动［14-15］，本文采用NUMECA软件进行CFD计算，湍流模型采用S-A一方程模型，时间离散采用四阶显式Runge-Kutta模型，同时采用具有二阶和四阶人工黏性项的有限体积中心差分格式控制空间离散化过程中的伪数值振荡，利用多重网格、局部时间步长和隐残差加快算法的收敛。

网格生成采用NUMECA中的Autogrid5模块，主拓扑采用H＆I，叶尖间隙网格采用HO拓扑，近壁面第一层网格厚1 μm，量纲一的壁面距离Y+≤5，叶片表面和端壁设置为无滑移边界条件，边界条件如下：压气机进口总温度为293 K，总压为101 325 Pa，进口的方向设置为轴向，出口的背压取平均静压，通过逐渐增大出口的背压，使得从堵塞点向近喘振点推进计算，取第一个发散点之前的收敛点为近喘振点。为保证流场计算时的网格质量，对叶轮在额定转速下单通道的网格独立性进行了验证。如图4所示，103万个网格和150万个网格的计算结果基本一致，说明当网格总数N达到103万时，再增多网格对气动性能影响很小。为节约时间成本，后续优化过程均选择103万网格的结构作为网格模板进计算，优化时所有样本数据的计算方法均采用相同的边界条件和网格配置，生成的叶片网格如图5所示。

在自动优化过程中，NUMECA软件的网格划分和流场计算功能通过程序代码调用实现：首先找出NUMECA软件中网格模板和流场计算的配置文件路径；然后将网格划分、流场计算功能的.exe文件和配置文件，按图6中的形式写入.bat批处理文件中；在优化算法每次进化出新的样本数据后，得到新叶轮；最后，调用.bat批处理文件，完成网格划分和流场计算，实现自动优化。

2.4 优化流程

双Bezier参数化配置方法如下［7］：利用2个6×3阶的单位化Bezier曲面对主叶片和分流叶片分别進行曲面参数化。如图7所示，单位化Bezier曲面的ξ轴对应叶片翼展方向，η轴对应叶高方向，每个曲面在ξ方向上设7个控制顶点（0、0.1、0.3、0.5、0.7、0.9、1.0），在η方向上设4个点（0、0.4、0.7、1.0），以绿色压力面上的控制顶点作为优化变量，以Bezier曲面的法向为设计变量的寻优方向，吸力面控制顶点（粉色）与压力面控制

顶点（绿色）的变化保持一致，优化变量的变化范围如表6所示。

采用MMOA算法（参数配置见表7）、双Bezier曲面参数化方法、CFD流场求解器求解等熵效率的最大值。图8所示的基于多代理模型优化技术流程如下：①采用拉丁超立方采样设计初始化220个种群变量个体，生成220个不同叶片几何构型的初始离心叶轮；②按照2.3节生成的网格模板，利用NUMECA软件对离心叶轮进

行网格划分；③流场计算采用NUMECA的Fine/Turbo模块，对网格划分完的离心叶轮进行气动性能的模拟计算，得到适应度评估值，并将每个变量个体及其适应度评估值组成一组样本数据，得到全局样本数据集G；④基于全局样本数据集G构建PR_G、Kriging_G和RBF_G模型和集成MSM_G模型，利用PSO算法快速求出MSM_G模型的不确定性最大样本，对其进行双Bezier曲面参数化生成新的离心叶轮，按照步骤②、③对新叶轮进行耗时的模拟评估，得到一组不确定性最大的样本数据，将其填充到全局样本集数据G，并更新PR_G、Kriging_G、RBF_G模型和集成MSM_G模型；⑤利用PSO算法快速求解出全局最优样本变量个体，并对其进行双Bezier曲面参数化，生成新的离心叶轮，按照步骤②、③对新叶轮进行昂贵计算，得到一组全局最优样本数据，将其填充到全局样本数据集G，并更新PR_G、Kriging_G、RBF_G模型和集成MSM_G模型；⑥重复步骤⑤，当全局最优样本不能进一步改进时，将所有优于初始样本的数据组成局部样本数据集L，并构建PR_L、Kriging_L、RBF_L模型和集成MSM_L模型；⑦利用PSO算法快速求解出局部最优样本变量个体，对其进行双Bezier曲面参数化，生成新的离心叶轮，按照步骤②、③对新叶轮进行昂贵计算，得到一组局部最优样本数据，将其填充到局部样本数据集L和全局样本集G，并更新PR_L、Kriging_L、RBF_L模型和集成MSM_L模型；⑧重复步骤⑦，当局部最优样本不能进一步改进时，自动循环步骤④～⑦，直到全局样本数据达到440组，选取样本数据中的最优解并生成最佳叶轮几何外形。

为对比MMOA与传统算法的计算效果，利用叶轮机械常用的PSO算法对同一叶轮进行优化设计。优化流程中，除算法不同外，参数化方法、网格生成方法、数值计算模型、数值求解器、设计变量、设计空间等均保持不变，PSO的优化流程如图9所示，参数配置如表8所示。

2.5 优化结果及分析

2.5.1 优化前后气动性能变化

分别采用MMOA和PSO对上述对象进行优化，得到的实验数据如表9、表10所示：由对比实验数据可知，MMOA与PSO的优化效果相近，但计算效率上有了大幅的提高，迭代减少了56%，运行总时间缩短了112h。这表明多代理模型优化技术可解决离心压气机叶轮优化设计过程中的昂贵计算难题。图10是MMOA优化前后气动性能对比图，结合表9可知，气动性能曲线有了整体上移，额定工况的等熵效率提高了0.73%，质量流量增加了2.49%，总压比增加了0.18%，喘振裕度提高了1.1%，优化后气动性能改善较为明显，证明了该优化方法的有效性。

2.5.2 优化前后叶片几何外形变化

优化前后的离心叶轮主叶片和分流叶片几何外形如图11所示，沿着叶高方向，主叶片中下部分弯向压力面，中截面基本不变，中上部分弯向吸力面；沿着叶高方向，分流叶片叶根部分弯向压力面，中上部分弯向吸力面。叶型和叶片外形的变化势必引起流道结构的变化，从而使流场结构和气动性能发生改变。

2.5.3 流场分析

叶高10%处B2B流面的相对马赫数如图12所示，优化后，区域A、B、C、D、E、F、G的相对马赫数增大，低速区域减小，有利于减少逆压梯度，使分离区延后。叶高10%处B2B流面的熵值如图13所示，H1、H2、J区域的高熵值区域减小，主叶片压力面和分流叶片吸力面之间通道的下游气动效率改善明显。

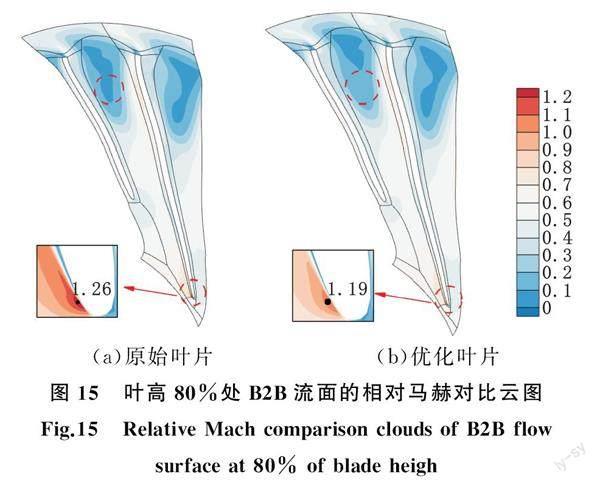
如图14、图15所示，MMOA优化后的入口气流匹配性增强，正攻角减小，相对马赫数的最大值和高值区域均有所减小，激波损失降低。由主叶片静压分布曲线可知，优化后吸力面的静压爬坡变缓，逆压梯度减小，分离区延后，降低流动损失。

3 结论

（1）基于PR模型、Kriging模型和RBF模型创建了多代理模型优化算法，利用在线驱动方法、模型管理策略及粒子群算法对样本数据进行填充，获得了高精度的预测模型。基于30次独立重复性实验和5个经典测试问题，对比分析了多代理模型优化算法与常用元启发式算法性能表现，实验数据表明多代理模型优化算法仅需11d次（d为设计变量维数）迭代即可得到理想解，明显减少了迭代，验证了多代理模型优化算法高效求解较大规模优化问题的有效性。

（2）建立了离心叶轮复杂曲面叶片几何构型与Bezier曲面的映射模型，通过扰动Bezier曲面来控制叶片形状，得到了新的叶片几何构型。与传统型线参数化相比，双Bezier曲面参数化方法具有明显的降维效果，利用少量设计变量即可实现叶片的灵活构型；增加了径向约束，有利于生成光滑叶片。

（3）基于多代理模型技术、双Bezier曲面参数化方法及计算流体动力学，构建了离心叶轮高效气动优化设计方法，以等熵效率最大化为优化目标，求解了离心叶轮复杂曲面叶片的最佳几何构型。优化后，气动性能曲线整体上移，综合性能改善较为明显：额定工况等熵效率提高了0.73%，总压比增加了0.18%，喘振裕度增加了1.1%，流场结构得到优化。对比分析了多代理模型优化算法和粒子群算法的优化结果，实验数据表明多代理模型优化算法可提高计算效率达54.9%，验证了该优化设计方法的时效性。

参考文献：

［1］童哲铭， 陈尧， 童水光， 等. 基于NSGA-Ⅲ算法的低比转速离心泵多目标优化设计［J］. 中国机械工程， 2020， 31（18）：2239-2246.

TONG Zheming， CHEN Yao， TONG Shuiguang， et al. Multi-objective Optimization Design of Low Specific Speed Centrifugal Pumps Based on NSGA-Ⅲ Algorithm［J］. China Mechanical Engineering， 2020， 31（18）：2239-2246.

［2］姜丙孝， 杨军虎， 王晓晖， 等. 基于RBF-HDMR模型与PSO算法的液力透平叶片优化［J］. 机械工程学报， 2022， 58（12）：283-292.

JIANG Bingxiao， YANG Junhu， WANG Xiaohui， et al. Blades Optimization of Pumps as Turbines Based on RBF-HDMR Model and PSO Algorithm［J］. Journal of Mechanical Engineering， 2022， 58（12）：283-292.

［3］HOSSEINIMAAB S M， TOUSI A M. Optimizing the Performance of a Single-shaft Micro Gas Turbine Engine by Modifying Its Centrifugal Compressor Design［J］. Energy Conversion and Mmanagement， 2022， 271：116245.

［4］BAI L， YANG Y， ZHOU L， et al. Optimal Design and Performance Improvement of an Electric Submersible Pump Impeller Based on Taguchi Approach［J］. Energy， 2022， 252：124032.

［5］BASHIRI M， DERAKHSHAN S， SHAHRABI J. Design Optimization of a Centrifugal Pump Using Particle Swarm Optimization Algorithm［J］. International Journal of Fluid Machinery and Systems， 2019， 12（4）：322-331.

［6］孔庆国， 杜旭博， 羌晓青， 等. 基于中弧线曲率控制的压气机叶型优化［J］. 推进技术， 2020， 41（8）：1740-1747.

KONG Qingguo， DU Xubo， QIANG Xiaoqing， et al. Compressor Airfoil Optimization Based on Camber Curvature Control［J］. Journal of Propulsion Technology， 2020， 41（8）：1740-1747.

［7］劉基盛， 李威， 计良， 等. 一种新颖的离心叶轮多工况气动优化设计方法［J］. 推进技术， 2022， 43（11）：126-139.

LIU Jisheng， LI Wei， JI Liang， et al. A Novel Multi-condition Aerodynamic Optimization Design Method for Centrifugal Impeller［J］. Journal of Propulsion Technology， 2022， 43（11）：126-139.

［8］AYE C M， PHOLDEE N， YILDIZ A R， et al. Multi-surrogate-assisted Metaheuristics for Crashworthiness Optimisation［J］. International Journal of Vehicle Design， 2019， 80（2/4）：223-240.

［9］CHRISTELIS V， KOPSIAFTIS G， MANTOGLOU A. Performance Comparison of Multiple and Single Surrogate Models for Pumping Optimization of Coastal Aquifers［J］. Hydrological Sciences Journal， 2019， 64（3）：336-349.

［10］LI M Y， TANG J J， MENG X W. Multiple Surrogate-model-Based Optimization Method Using the Multimodal Expected Improvement Criterion for Expensive Problems［J］. Mathematics， 2022， 10（23）：4467.

［11］YIN J N， TSAI F T C， LU C H. Bi-objective Extraction-injection Optimization Modeling for Saltwater Intrusion Control Considering Surrogate Model Uncertainty［J］. Water Resources Management， 2022， 36（15）：6017-6042.

［12］何西旺， 杨亮亮， 冉仁杰， 等. 基于多评价标准的代理模型综合比较研究［J］. 机械工程学报， 2022， 58（16）：403-419.

HE Xiwang， YANG Liangliang， RAN Renjie， et al. Comparative Studies of Surrogate Models Based on Multiple Evaluation Criteria［J］. Journal of Mechanical Engineering， 2022， 58（16）：403-419.

［13］WANG H， JIN Y， DOHERTY J. Committee-based Active Learning for Surrogate-assisted Particle Swarm Optimization of Expensive Problems［J］. IEEE Transactions on Cybernetics， 2017， 47（9）：2664-2677.

［14］杨登峰， 潘俞舟， 王贵召， 等. 分体滑动导叶可调涡轮激波与载荷波动机制［J］. 中国机械工程， 2020， 31（15）：1778-1786.

YANG Dengfeng， PAN Yuzhou， WANG Gui-zhao， et al. Mechanism of Shock and Load Fluctuation of Variable Nozzle Turbines with Split Sliding Guide Vanes［J］. China Mechanical Engineering， 2020， 31（15）：1778-1786.

［15］罗钜， 郭福水. 民用涡扇发动机总体多学科设计优化研究［J］. 中国机械工程， 2019， 30（15）：1813-1820.

LUO Ju， GUO Fushui. Study on Multi-disciplinary Design Optimization on Civil Turbofan Engines［J］. China Mechanical Engineering， 2019， 30（15）：1813-1820.

（编辑 张 洋）

作者简介：

刘基盛，男，1986年，博士。研究方向为数字化设计与制造、现代机械设计方法。發表论文10余篇。E-mail：liujisheng@ustb.edu.cn。

贾志新（通信作者），男，1968年，教授。研究方向为数字化设计与制造、智能制造、数控制造装备设计及其可靠性技术。发表论文100余篇。E-mail：jiazhixin@me.ustb.edu.cn。

收稿日期：2022-10-27

基金项目：国家自然科学基金（51775036）；广东省基础与应用基础研究基金（2022A1515110055）