显式动力学驱动的轴承变工况故障诊断方法

张龙　张号　王朝兵　王晓博　文培田　赵丽娟

摘要：实际工程应用中，旋转机械通常处于变工况状态，不同工况样本特征分布的差异限制了故障诊断模型的应用范围。为解决变工况下特征分布不一致的问题，提出了显式动力学驱动的轴承变工况故障诊断方法。首先，采用有限元法仿真多工况、多故障类型的样本，通过冗余属性投影得到不同故障类型下的仿真投影矩阵；然后，利用仿真投影矩阵同步消除实测信号特征样本的复杂工况冗余信息；最后，结合支持向量机进行轴承变工况的故障诊断。通过两组变工况轴承数据集对所提方法进行验证，验证结果表明，仿真投影矩阵有效消除了冗余工况信息，投影后的故障诊断准确率达到100%。

关键词：滚动轴承；有限元分析；冗余属性投影；故障诊断

中图分类号：TH133.3

DOI：10.3969/j.issn.1004-132X.2023.08.013

Explicit Dynamics Driving Fault Diagnosis Method for Bearing Variable Conditions

ZHANG Long1 ZHANG Hao WANG Chaobing1，2 WANG Xiaobo1 WEN Peitian1 ZHAO Lijuan1

Abstract： In practical engineering applications， rotating machines were usually in variable conditions， and the feature distribution of samples in different conditions was differentiated， which limited the application scope of fault diagnosis models. In order to solve the problem of inconsistent feature distribution under variable conditions， a method of bearing failure diagnosis of variable conditions under explicit dynamics was proposed. Firstly， the finite element method was used to simulate sample of multiple conditions and multiple fault types， and the simulation projection matrix under different fault types were obtained by NAP. Secondly， the complex working condition nuisance information of the measured signal feature samples were eliminated simultaneously by simulation projection matrix. Finally， the bearing fault diagnosis was performed based on support vector machine. The proposed method was validated by two sets of variable condition bearing data sets. The test results show that the simulation projection matrix may effectively eliminate the nuisance condition information， and the accuracy of fault diagnosis after projection reach 100%.

Key words： rolling bearing； finite element analysis； nuisance attribute projection（NAP）； fault diagnosis

0 引言

随着工业智能化的发展，Symbol`@@工业装备的一体化程度越来越高，关键零部件发生故障将会带来严重后果。滚动轴承的故障率高达30%［1-2］，为避免轴承故障带来的人员伤亡与经济损失，需通过智能诊断算法对复杂工况下的轴承状态进行监测。振动信号能有效反映轴承健康状态，因此基于振动信号的故障诊断备受关注［3-5］。传统的旋转机械故障诊断方法主要有信号处理、特征提取与模式识别、深度学习［6］。

ZHAO等［7］为提取强背景噪声环境下的故障信息，提出一种自适应增强稀疏周期性分组的回归算法来增强故障脉冲的特征。侯钰哲等［8］先通过Filter和改进灰狼优化算法两次筛选高维特征集来凸显故障特征，再通过支持向量机实现故障诊断。张龙等［9］将具有空间处理能力与时序处理能力的CNN与GRU相结合，以同时提取空间与时序融合特征，实现了“端到端”的故障诊断。上述研究虽取得了良好的诊断结果，但实际工程应用中的轴承工况难以保持恒定，因此考虑变工况对故障诊断结果的影响更具工程意义。

轴承服役过程中，离散或连续载荷、转速变化等因素给轴承的故障诊断带来新的困难［10-11］。针对该类问题，张旭辉等［12］将快速谱峭度与阶次分析相结合，将时域非平稳信号转为角域信号来消除频率模糊，实现了变工况下轴承故障特征的提取。XU等［13］对小波包处理后的特征信息声发射信号及振动信号进行融合，在轉速和载荷变化工况下实现了轴承故障类型的识别。YANG等［14］结合迁移学习与深度学习方法，利用联合最大平均偏差准则和域自适应网络使源域和目标域相匹配，实现了变工况的故障诊断。上述学者从保留工况信息的角度出发，研究了变工况下的轴承故障诊断方法。

变工况下的特征分布存在差异，这使得故障诊断准确率和泛化能力存在一定的不足。

为解决上述问题，本文从消除工况冗余信息的角度出发，提出显式动力学法驱动的变工况故障诊断方法。冗余属性投影（nuisance attribute projection，NAP）作为一种消除冗余信息的方法，最初用于语言识别、人脸识别［15-16］。SOLOMONOFF等［17］、JIANG等［18］将其引入轴承的故障诊断，以消除变工况信号特征的冗余信息。NAP算法通过离散载荷、转速构建的投影矩阵消除工况信号特征的冗余信息。HUANG等［19］通过试验台预先获取离散变转速轴承的振动信号，采用NAP得到变转速数据集的投影矩阵，进而得到投影后的特征空间，达到消除工况冗余信息的目的。LYU等［20］预先获取不同通道的实测信号，通过多元经验模态分解得到本征模态分量，然后采用NAP得到可消除通道和工况冗余信息的投影矩阵，进而得到投影后的特征空间，将其输入加权极限学习机模型，最终实现变工况的故障诊断。

实际应用中，对于转速、载荷呈离散变化的轴承，需预先获取其数据样本，然后构建投影矩阵来消除离散工况的冗余信息；对于转速、载荷呈连续变化的轴承，需先获取包含载荷、转速范围的离散工况数据样本，然后构建投影矩阵以消除连续工况振动信号特征的冗余信息。因此基于已有的数据样本构建投影矩阵具有一定的局限性，且同时消除离散的转速与载荷、连续变化的转速与载荷的冗余工况信息是困难的。目前，有限元法已应用于轴承故障诊断［21］，为消除复杂工况下的冗余信息提供了新的解决途径。

1 轴承动力学模型的建立与可靠性分析

1.1 轴承动力学模型的建立

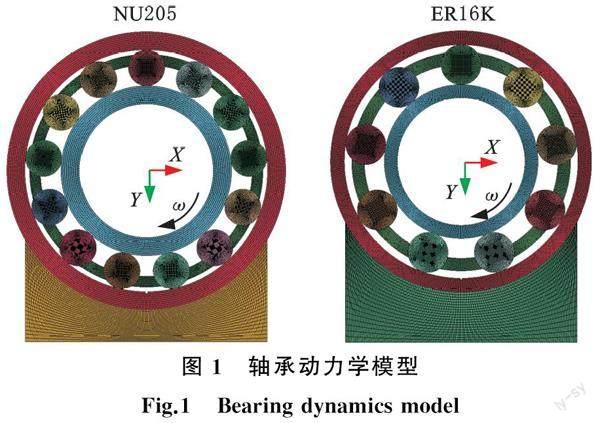
建立NU205、ER16K轴承的二维显式动力学模型（模拟轴承故障状态下的仿真信号），并将故障简化为矩形凹坑。 NU205轴承的几何参数如下：节圆直径38.75 mm，滚动体直径6.75 mm，滚动体个数13，接触角0°；外圈、内圈和滚动体的材料为GCr15，保持架材料为黄铜。ER16K轴承的几何参数如下：节圆直径38.52 mm，滚动体直径7.94 mm，滚动体个数9，接触角0°；各部件材料均为F1碳钢。

根据实际工况对轴承座进行简化，外圈过盈配合安装在轴承座中，在内圈内表面施加径向（Y轴正向）载荷，在内圈内表面施加顺时针方向的转速，轴承信号的采样频率为48 kHz。为更好地反映滚动体与内圈和外圈接触时的振动特性，将网格进行细化，shell163壳单元的整体网格尺寸为0.25 mm，接触部位细化网格尺寸为0.1 mm。NU205、ER16K轴承动力学模型见图1。

1.2 轴承动力学模型的可靠性验证

轴承显式动力学模型的可靠性保证了研究结果的可靠性，因此验证轴承动力学模型的有效性尤为必要。二维轴承模型为点点接触，采集的振动信号幅值较大［22］。分别对NU205轴承（转速1000 r/min）、ER16K轴承（转速1200 r/min）的外圈振动信号进行包络谱分析，得到的轴承仿真信号如图2、图3所示。从图2b、图3b中看到，仿真信号包络谱均出现了故障特征频率及其倍频。

轴承外圈理论故障特征频率为

式中，d1为滚动体直径；n为内圈转速；d2为节圆直径；Z为滚动体个数；α为接触角。

将NU205轴承的参数代入式（1），得到外圈的理论故障特征频率为89.3 Hz。仿真得到的外圈故障特征频率为89.9 Hz，理论值与仿真值的相对误差为0.7%。同理可得ER16K轴承外圈的理论故障特征频率为71.4 Hz，仿真故障特征频率为70 Hz，两者的相对误差1.96%。较小的误差说明了轴承动力学模型的准确性。

2 显式动力学驱动的仿真投影矩阵

2.1 NAP算法

由于变工况的干扰，原始信号的特征空间包含有效的故障信息，以及由工况变化引起的冗余信息。NAP的关键是确定投影矩阵P，通过投影消除特征样本的工况冗余信息，并尽可能多地保留故障信息。NAP算法原理见图4。

定义N维特征空间，构造N×m维的特征矩阵F=［F1 F2 … Fm］，Fm为工况m下的特征样本。投影后的特征矩阵Fnew由F与投影矩阵P构成：

2.2 轴承变工况诊断原理

实际工程应用中，轴承运行过程中的载荷和转速多处于变化状态，为实现变工况轴承故障的准确诊断，使用显式动力学法构建轴承动力学模型，仿真多工况、多故障类型的振动信号并对其进行归一化处理。通过NAP获得不同故障类型下的仿真投影矩阵，将实测信号特征样本进行投影，消除工况冗余信息的影响。将变工况投影后的已知样本作为训练集，将变工况投影后的未知样本作为测试集，使用支持向量机诊断变工况下的轴承故障。基于仿真投影矩阵消除实测信号冗余信息的故障诊断见图5。

3 投影矩阵的验证及获取

不同轴承的应用场合不同，针对待诊断轴承，构建动力学模型的参数及工况一致性是确保变工况轴承故障诊断准确率的前提。本节以ER16K型号轴承说明冗余信息的消除及仿真投影矩阵的获取。

为获得不同故障类型对应的仿真投影矩阵，借助有限元法仿真3种（正常、外圈故障、内圈故障）轴承的动力学模型（每种故障有5种不同转速）。工况信息为：载荷1000 N，转动频率10 Hz、15 Hz、20 Hz、25 Hz、30 Hz。采样频率48 kHz，仿真时间0.2 s。外圈故障的时域仿真信号见图6。3种故障类型中，每类工况均有10组样本。通过NAP算法处理，得到相应的仿真投影矩阵。

为验证NAP去除同种故障类型、不同工况冗余信息的效果，本文提取29个常用特征进行故障类型的识别。这29个特征分别为11个时域特征、包絡谱熵、幅值谱熵、8个节点能量及能量熵［23］。每个工况10组样本，5类工况的权重矩阵维度为50×50。由图7看到，品质因子D随特征维数d的增大而减小，d大于22时，D趋于稳定，因此确定d为22，将确定的d代入式（3）可得仿真投影特征矩阵。

由图8a看出，投影前，不同转速下的特征幅值分布较为离散。由图8b看出，投影后，特征幅值分布的离散程度有明显的减小，不同工况下的特征幅值几乎一致。仿真结果验证了仿真投影矩阵消除工况冗余信息的有效性。

不同故障类型的特征投影前后的结果见图9。由图9a看出，投影前，不同故障类型的个别特征幅值存在差异，大部分特征的幅值几乎一致。由图9b看出，投影后，不同故障类型的大部分特征幅值被有效区分，这表明不同故障类型的特征信息被保留。

4 试验分析

仿真信号与实测信号的幅值存在差异，为保证得到的仿真投影矩阵能消除实测信号样本的冗余信息，对仿真信号与实测信号进行归一化处理，将信号幅值转换到［0，1］区间内。通过仿真信号的特征矩阵得到仿真投影矩阵，借助仿真投影矩阵消除实测信号特征矩阵的冗余信息。冗余信息消除后的特征样本可用于故障诊断。

为验证所提方法在变工况轴承故障诊断的有效性，采用深度子领域自适应网络［24-25］（deep subdomain adaptive network，DSAN）进行对比实验，比较单工况和复合工况下的故障识别效果。

4.1 离散变转速、变载荷的实验分析

试验数据来自图10所示的旋转机械故障模拟试验台。实验轴承为NU205，采样频率12 kHz，采样时间10 s。正常（N）、外圈故障（OF）、内圈故障（IF）、滚动体故障（BF）的轴承离散变工况如下：转速为700 r/min、1000 r/min、1300 r/min，载荷为800 N、1100 N、1500 N。

通过有限元法仿真该工况下的轴承信号，借助NAP得到仿真投影矩阵，达到同步消除振动信号转速、载荷等冗余信息的目的。增大轴承的径向载荷会影响转速，故仿真轴承的工况需符合载荷小时转速高的现象，因此动力学模型的仿真工况为800 N与1300 r/min、1100 N與1000 r/min、1500 N与700 r/min。

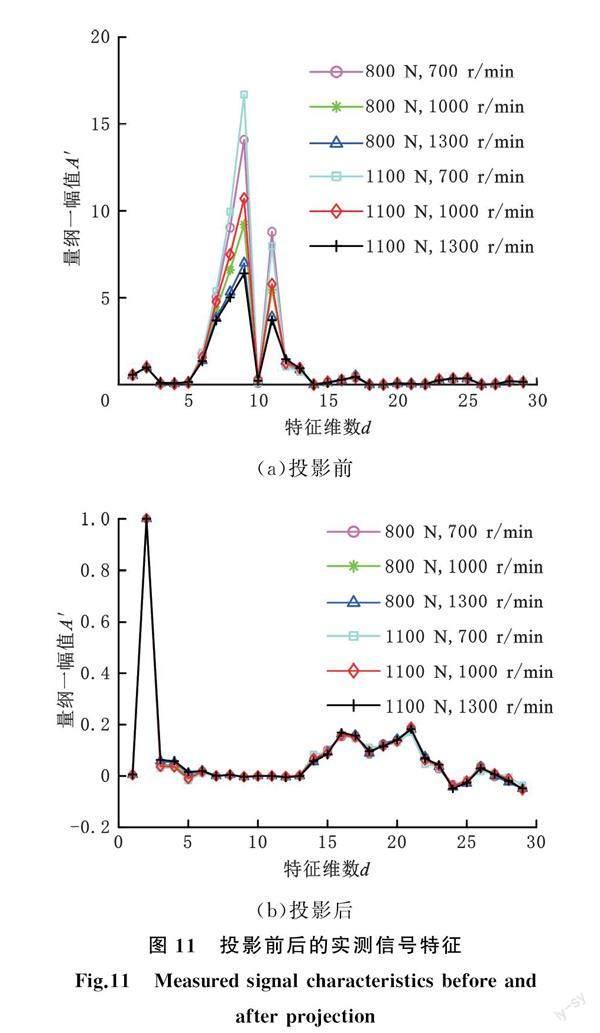
通过仿真4种轴承在3种不同工况下的振动信号，得到4种健康状态、不同工况的特征样本，经过NAP处理得到正常投影（normal projection，NP）、外圈故障投影（outer fault projection，OFP）、内圈故障投影（inner fault projection，IFP）、滚动体故障投影（bearing rolling element fault projection，BFP）的投影矩阵。实测信号特征样本经过仿真投影矩阵投影可消除工况的冗余信息。以外圈故障为例，6种工况投影前后的特征值分布如图11所示，OFP同步消除了离散载荷、转速带来的冗余信息。

OFP在消除振动信号含有的工况冗余信息的同时保留了故障信息。由图12可以看出，投影后，幅值差异更大，不同故障类型的特征幅值离散程度更显著，说明投影后的特征空间保留了故障信息。

以上分析确定了仿真投影矩阵能同步消除离散载荷、转速的冗余信息的有效性，因此可以将其应用到试验数据中。试验得到的试验数据包括4种故障，每种故障对应9种工况，每种工况有50组样本，每组样本有29个特征。将已知工况投影后样本作为训练集输入支持向量机进行训练，将未知工况投影后的样本作为测试集进行故障诊断。将DSAN作为对比方法来说明仿真投影矩阵消除信号特征冗余信息的优势。

4.1.1 单工况故障诊断

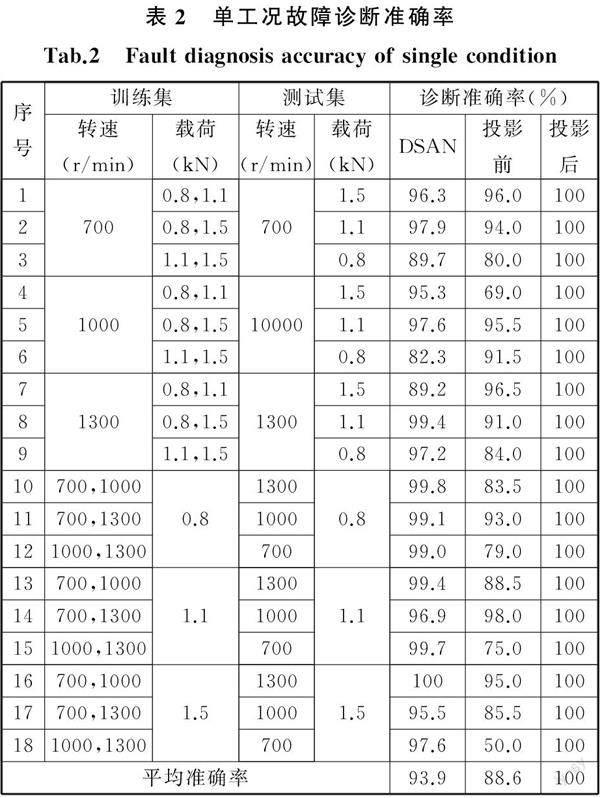
离散工况的故障诊断诊断结果见表2。

由转速700 r/min、1300 r/min（序号1～3、序号7～9）的诊断结果可以看出，特征样本投影前，测试集载荷大于训练集载荷时，识别准确率最高；测试集载荷处于训练集载荷之间时，识别准确率有所下降；测试集载荷小于训练集载荷时，识别准确率最低。转速1000 r/min时，测试集载荷大于训练集载荷的识别准确率仅为69.0%，导致准确率较小的原因是轴承在该工况下，旋转不稳定导致采集的振动信号较差。特征样本投影后，消除了载荷变化的影响，不管测试集与训练集数据是否存在交集，故障诊断准确率均达到100%。相比于投影前，通过DSAN方法得到故障诊断精度较高。转速不变的情况下，DSAN的故障诊断平均准确率为93.9%，投影前故障诊断的平均准确率为88.6%，投影后故障诊断的平均准确率为100%。

由载荷800 N、1100 N（序号10～15）的诊断结果可以看到，特征样本投影前，测试集转速处于训练集转速之间时，识别准确率最高；测试集转速大于训练集转速时，识别准确率有所下降；测试集转速小于训练集转速时，识别准确率最低。载荷为1500 N时，测试集转速小于训练集转速时的识别准确率仅为50%，可能的原因是不同转速下，采集得到的数据样本特征分布差异较大；特征样本投影消除了转速的影响，不管测试集与训练集的数据集是否存在交集，故障诊断准确率均达到100%。相比于投影之前，采用DSAN方法的轴承故障诊断准确率有很大的提升，说明DSAN方法在单工况、变转速下的故障诊断效果更好。载荷不变的情况下，序号1～9的平均诊断准确率中，DSAN的故障诊断平均准确率为98.6%，投影前的故障诊断平均准确率为83.1%，投影后的故障诊断平均准确率为100%。

单工况故障诊断的分析结果说明：转速对故障诊断准确率的影响大于载荷，仿真投影矩阵可消除实测特征样本的冗余信息。

4.1.2 复合工况故障诊断

工程应用中，转速、载荷均变化的情况时有出现，因此分析复合工况变化下的故障诊断效果是必要的。测试集载荷、转速同时变化的故障诊断结果见表3。

根据表3，将9组数据中每组的转速和载荷组合为4组样本（训练集），将每组中的转速和载荷均与训练集不同的样本作为测试集。由表3看出，特征样本投影之前，测试集数据中的转速高于或位于训练集之间时，无论测试集载荷与训练集区间是否存在交集，诊断准确率均大于82.5%；测试集低于训练集时，诊断准确率明显下降，最低为67.5%。复合工况变化下，相比于投影前，DSAN方法故障诊断结果更高，诊断准确率均在87.1%以上。投影后，测试集与训练集的工况区间差异不再是影响故障诊断的因素，将影响诊断准确率的复合工况冗余信息消除后，诊断准确率达到了100%。

复合工况故障诊断结果的分析说明：转速对诊断准确率的影响更大，且仿真投影矩阵具有同步消除转速、载荷冗余信息的能力。

4.2 连续变转速试验数据

试验数据集来自渥太华大学机械工程学院，试验台见图13，其详细参数及描述见文献［26］。转速分别为持续增加（A）、持续减少（B）、先增后减（C）、先减后增（D）。不同健康状态下的转速范围见表4。

根据表4可知ER16K轴承转频区间为10.3～28.6 Hz，为有效消除实测信号包含的工况冗余信息，将仿真轴承转频设置为10 Hz、15 Hz、20 Hz、25 Hz、30 Hz。

通过仿真3种健康状态轴承的振动信号，获得仿真投影矩阵。计算相同健康状态、不同工况的特征样本，NAP处理后得到正常、外圈故障、内圈故障的投影矩阵。由图14可看出，仿真投影矩阵有效消除了连续变工况中的冗余信息，减小了特征值的分布距离。由图15可看出，投影后不同健康状态的幅值区分度较投影前大，保留了故障信息。

上述分析验证了仿真投影矩阵消除连续变转速冗余信息的有效性，可将其应用到试验数据中。根据试验过程，得到的试验数据包括3种健康状态，每种健康状态对应4类工况，每类工况有100组样本，每组样本有29个特征。仿真投影矩阵可消除原始特征样本的冗余信息。将工况特征已知的样本输入支持向量机进行训练，将工况特征未知的样本作为测试集进行故障诊断。为说明所提方法的效果，采用主流的迁移学习模型——深度子领域自适应方法作对比，验证仿真投影矩阵用于变工况故障诊断的优势。

4.2.1 单工况故障诊断

训练集为一组或多组连续变工况的数据样本，测试集为一组与训练集不同的连续变工况的数据，对多种连续变转速轴承故障进行诊断，诊断结果见表5。

由表5可看出，将单个连续变工况作为训练集与测试集时，对于投影前的特征样本，测试集转速范围处于训练集转速范围之间时，故障诊断准确率均在97.7%之上；测试集转速下限低于训练集下限时，诊断准确率急剧下降，序号4的平均诊断准确率仅为78.9%。将多个转速工况作为测试集，同样出现测试集与训练集的转速范围重合导致诊断准确率变化的情况。这说明转速的连续变化影响了故障诊断准确率的提升。测试集与训练集均为连续变转速时，转速区间存在重合，因此投影前的单工况平均诊断准确率达到94.3%。对于DSAN方法，连续变工况下，测试集与训练集的转速区间是否交叉对故障类型识别的影响较小，故障诊断精度均在91.0%以上；多个变转速工况作为训练集、单个变转速工况作为测试集时，诊断准确率急剧减小，最高仅为67.4%。对于投影后的特征样本，无论训练集与测试集的转速范围是否存在交集，诊断准确率均达到100%，这验证了仿真投影矩阵用于单工况、连续变转速故障诊断的优越性。

4.2.2 复合工况故障诊断

轴承实际工作过程中，其转速可能处于多个连续变化区间内。为验证所提方法在该种情况下的有效性，对两种不同的连续变转速工况测试集进行故障诊断，结果见表6。

由表6看到，投影前，测试集两种转速在训练集之间或高于训练集时，准确率均超过99%；测试集的变转速范围小于训练集时，诊断准确率降低；转速变化趋势不是影响诊断准确率的主要原因，测试集与训练集的转速区间是否存在交集对诊断准确率的影响更大。对于DSAN方法，训练集和测试集均为多个变转速工况时，诊断准确率较低，最高仅为69.8%。这说明DSAN方法对连续变转速的复合工况故障诊断效果较差，无法消除多域数据分布差异。投影后，任意复合工况变化具有的冗余信息均被消除，诊断准确率达到100%。

5 结论

（1）将借助轴承动力学模型仿真的多工况、多故障类型数据样本特征输入NAP算法得到仿真投影矩阵，以消除实测信号特征的冗余信息。

（2）使用仿真投影矩阵获取两组试验数据集（离散变载荷、转速，以及连續变转速）的样本特征表明，仿真投影矩阵能有效消除单工况和复合工况的振动信号特征包含的冗余信息。

（3）对离散变工况和连续变工况实测样本进行了单工况、复合工况故障诊断，并将其与深度子领域自适应方法进行对比，故障诊断结果说明了仿真投影矩阵用于变工况故障诊断的有效性。

参考文献：

［1］陈是扦， 彭志科， 周鹏. 信号分解及其在机械故障诊断中的应用研究综述［J］. 机械工程学报， 2020， 56（17）：91-107.

CHEN Shiqian， PENG Zhike， ZHOU Peng， et al. Review of Signal Decomposition Theory and Its Applications in Machine Fault Diagnosis［J］. Journal of Mechanical Engineering， 2020， 56（17）：91-107.

［2］LEI Y， HE Z， ZI Y. A New Approach to Intelligent Fault Diagnosis of Rotating Machinery［J］. Expert Systems with Applications， 2008， 35（4）：1593-1600.

［3］SINGH V， VERMA N K. Intelligent Condition-based Monitoring Techniques for Bearing Fault Diagnosis［J］. IEEE Sensors Journal， 2020， 21（14）：15448-15457.

［4］李华， 刘韬， 伍星， 等. 相关奇异值比的SVD在轴承故障诊断中的应用［J］. 机械工程学报， 2021， 57（21）：138-149.

LI Hua， LIU Tao， WU Xing， et al. Application of SVD Based on Correlated Singular Value Ratio in Bearing Fault Diagnosis［J］. Journal of Mechanical Engineering， 2021， 57（21）：138-149.

［5］GAO Y， YU D. Fault Diagnosis of Rolling Bearing Based on Laplacian Regularization［J］. Applied Soft Computing， 2021， 111：107651.

［6］LEI Z， WEN G， DONG S， et al. An Intelligent Fault Diagnosis Method Based on Domain Adaptation and Its Application for Bearings under Polytropic Working Conditions［J］. IEEE Transactions on Instrumentation and Measurement， 2020， 70：1-14.

［7］ZHAO Z， WU S， QIAO B， et al. Enhanced Sparse Period-group Lasso for Bearing Fault Diagnosis［J］. IEEE Transactions on Industrial Electronics， 2018， 66（3）：2143-2153.

［8］侯钰哲， 李舜酩， 龚思琪. 滚动轴承故障特征选择的Filter与改进灰狼优化混合算法［J/OL］. 计算机集成制造系统［2022-04-12］. https：∥kns. cnki. net/kcms/detail/11. 5946. TP. 20220411. 1813. 036. html.

HOU Yuzhe， LI Shunming， GONG Siqi. Hybrid Algorithm of Filter and Improved Gray Wolf Optimization for Fault Feature Selection of Rolling Bearing［J/OL］. Computer Integrated Manufacturing Systems［2022-04-12］. https：∥kns. cnki. net/kcms/detail/11. 5946. TP. 20220411. 1813. 036. html.

［9］张龙， 甄灿壮， 易剑昱， 等. 双通道特征融合CNN-GRU齿轮箱故障诊断［J］. 振动与冲击， 2021， 40（19）：239-245.

ZHANG Long， ZHEN Canzhuang， YI Jianyu， et al. Dual-hannel Feature Fusion CNN-GRU Gearbox Fault Diagnosis［J］. Journal of Vibration and Shock， 2021， 40（19）：239-245.

［10］APPANA D K， PROSVIRIN A， KIM J M. Reliable Fault Diagnosis of Bearings with Varying Rotational Speeds Using Envelope Spectrum and Convolution Neural Networks［J］. Soft Computing， 2018， 22（20）：6719-6729.

［11］HOU F， SELESNICK I， CHEN J， et al. Fault Diagnosis for Rolling Bearings under Unknown Time-varying Speed Conditions with Sparse Representation［J］. Journal of Sound and Vibration， 2021， 494：115854.

［12］張旭辉， 张超， 樊红卫， 等. 快速谱峭度结合阶次分析滚动轴承故障诊断［J］. 振动. 测试与诊断， 2021， 41（6）：1090-1095.

ZHANG Xuhui， ZHANG Chao， FAN Hongwei， et al. Improved Fault Diagnosis of Rolling Bearing by Fast Kurtogram and Order Analysis［J］. Journal of Vibration， Measurement & Diagnosis， 2021， 41（6）：1090-1095.

［13］XU Y， CAI W， XIE T. Fault Diagnosis of Subway Traction Motor Bearing Based on Information Fusion under Variable Working Conditions［J］. Shock and Vibration， 2021， 2021：5522887.

［14］YANG X， CHI F， SHAO S， et al. Bearing Fault Diagnosis under Variable Working Conditions Based on Deep Residual Shrinkage Networks and Transfer Learning［J］. Journal of Sensors， 2021， 2021：57144240.

［15］STRUC V， VESNICER B， MIHELIC F， et al. Removing Illumination Artifacts from Face Images Using the Nuisance Attribute Projection［C］∥2010 IEEE International Conference on Acoustics， Speech and Signal Processing. Dallas， 2010：846-849.

［16］VESNICER B， MIHELICˇ F. The Likelihood Ratio Decision Criterion for Nuisance Attribute Projection in GMM Speaker Verification［J］. EURASIP Journal on Advances in Signal Processing， 2008， 2008：1-11.

［17］SOLOMONOFF A， CAMPBELL W M， QUILLEN C. Nuisance Attribute Projection［J］. Speech Communication， 2007：7385151.

［18］JIANG H， CHEN J， DONG G. Hidden Markov Model and Nuisance Attribute Projection Based Bearing Performance Degradation Assessment［J］. Mechanical Systems and Signal Processing， 2016， 72：184-205.

［19］HUANG W， CHENG J， YANG Y. Rolling Bearing Fault Diagnosis and Performance Degradation Assessment under Variable Operation Conditions Based on Nuisance Attribute Projection［J］. Mechanical Systems and Signal Processing， 2019， 114：165-188.

［20］LYU Y， YANG D， YUAN R， et al. A Novel Multivariate Signal Processing-based Fault Diagnosis Approach of Rotating Machinery under Various Operating Conditions［J］. Measurement Science and Technology， 2022， 33（7）：075106.

［21］LIU X， HUANG H， XIANG J. A Personalized Diagnosis Method to Detect Faults in a Bearing Based on Acceleration Sensors and an FEM Simulation Driving Support Vector Machine［J］. Sensors， 2020， 20（2）：420.

［22］SINGH S， HOWARD C Q， HANSEN C H， et al. Analytical Validation of an Explicit Finite Element Model of a Rolling Element Bearing with a Localised Line Spall［J］. Journal of Sound and Vibration， 2018， 416：94-110.

［23］JIANG H， CHEN J， DONG G， et al. An Intelligent Performance Degradation Assessment Method for Bearings［J］. Journal of Vibration and Control， 2017， 23（18）：3023-3040.

［24］LI R， LI S， XU K， et al. Adversarial Domain Adaptation of Asymmetric Mapping with CORAL Alignment for Intelligent Fault Diagnosis［J］. Measurement Science and Technology， 2022， 33（5）：055101.

［25］董紹江， 朱朋， 裴雪武， 等. 基于子领域自适应的变工况下滚动轴承故障诊断［J］. 吉林大学学报（工学版）， 2022， 52（2）：288-295.

DONG Shaojiang， ZHU Peng， PEI Xuewu， et al. Fault Diagnosis of Rolling Bearing under Variable Operating Conditions Based on Subdomain Adaptation［J］. Journal of Jilin University（Engineering and Technology Edition）， 2022， 52（2）：288-295.

［26］HUANG H， BADDOUR N. Bearing Vibration Data Collected under Time-varying Rotational Speed Conditions［J］. Data in Brief， 2018， 21：1745-1749.

（编辑 张 洋）

作者简介：

张 龙，男，1980年生，教授。研究方向为机电和轨道交通装备状态监测与故障诊断。E-mail：longzh@126.com。

收稿日期：2022-05-02

基金项目：江西省自然科学基金（20212BAB204007）；江西省研究生创新资金（YC2021-S422）。