基于高斯模型和RMSD-DS的火炮反后坐装置故障诊断方法
魏剑峰, 张发平*, 卢继平, 杨向飞, 杨鹏楷
(1.北京理工大学 机械与车辆学院, 北京 100081; 2.北京理工大学 计算机学院, 北京 100081)
0 引言
火炮反后坐装置作为火炮的关键部件,承担着火炮射击时后坐能量的耗散与存储,以及复位炮身的作用[1-2]。战场中,作战环境的复杂性使得火炮反后坐装置故障频发,若未及时诊断并解决火炮反后坐装置故障,则会严重影响炮弹发射效率和射击精度[3],甚至贻误宝贵战机,引发严重的战场事故。因此,研究火炮反后坐装置的故障诊断具有重要意义。
火炮所处战场为复杂的变工况环境,变工况环境的多变性、不确定性等特点导致装备传感器采集的信息具有模糊性,给故障诊断工作带来困难。例如由于每发炮弹装药量的差异,导致正常状态下后坐位移、速度具有随机特性。目前反后坐装置故障诊断多以神经网络为工具开展相关工作[4-5]。神经网络虽然具有良好的自学习能力和自适应能力,但训练过程复杂,类似黑箱程序,处理火炮故障诊断中模糊信息的能力有限。高斯模型的提出为解决这一问题提供了思路,高斯模型中将信息的概率密度函数近似定义为高斯分布形式,可实现模糊信息的定量化表征,有效解决模糊性问题[6]。因此针对火炮反后坐装置的某类故障特性信号,可通过建立其高斯模型的方式确定各个故障发生概率。但由于火炮反后坐装置单一故障特性信号所蕴含的信息量有限,难以保证诊断精度。
为提升诊断精度,需要获取火炮反后坐装置的多个故障特性信号,开展基于融合的诊断工作。常用融合方法有Dempster-Shafer (DS)证据理论[7-9]、粗糙集[10]、神经网络[11]等,其中DS证据理论在融合过程中所表现的优越性让其在装备的故障诊断领域中得到广泛应用。但火炮所处战场环境中,由于变工况或其他干扰导致某些故障特性信号输出与实际情况不符,导致这类信息所对应的证据与其他输出信息所对应的证据产生高度冲突,若直接应用DS方法融合高度冲突的证据,则融合结果可能会产生与常理相悖的情况[12]。为解决DS方法的这一弊端,学者们主要从修改DS证据理论中的组合规则[13-15]和修改证据源[16-18]两方面着手对原有DS证据理论进行改进。修改组合规则方面,以Yager[13]为代表,通过将信息之间的冲突性分配给辨识框架里的未知集合来修改融合规则,以产生稳健的融合结果,但DS证据理论中的组合规则经过严密的数学推理得到,修改组合规则的方式并不合理。修改证据源方面,以Murphy[16]为代表,通过将各组证据简单平均的方式修改证据源,弱化了证据间的冲突,但该方法未考虑每个证据在融合决策过程中的重要性。文献[17-18]均是基于Murphy的思想对DS证据理论做了相关改进,但存在运算复杂、普适性缺乏等问题。
为解决上述问题,本文基于Murphy思想提出一种 RMSD-DS方法,结合高斯模型应用于火炮反后坐装置故障诊断中,实现信息模糊性的定量化表征以及高冲突证据融合下高可信性诊断工作。首先基于高斯模型,求解火炮反后坐装置的每个故障特征信号所对应证据的基本概率分配(BPA);然后提出一种基于RMSD-DS的融合方法,通过构造证据间RMSD冲突系数、定义证据重要度、赋于证据权重等途径对原始证据进行修正并求解得到加权平均新证据;最后采用DS组合规则进行融合新证据,得到火炮反后坐装置的诊断结果。
1 火炮反后坐装置的描述及运动过程建模
1.1 火炮反后坐装置的介绍
某型号火炮简易结构[19]如图1所示,火炮射击过程中,在反后坐装置与炮膛合力的作用下,后坐部分相对于炮架做后坐和复进运动,以保证火炮的稳定性和可靠性。
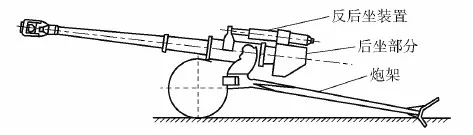
图1 火炮简易结构图Fig.1 Simple structure of a gun
反后坐装置由制退机、复进机两部分组成。其中,制退机主要由制退杆、节制环、制退筒等部件组成,制退机控制火炮后坐部分按照预定的受力和运动规律进行后坐和复进,保证火炮在射击过程中的稳定性。复进机由复进杆、制退液等组成,复进机在火炮的后坐过程中储存部分后坐能量,在火炮后坐过程结束后让后坐部分归回原位,保证火炮在后续射击过程中的可靠性。
反后坐装置典型故障状态有节制环磨损(WTR)、复进机漏气(GLR)和制退杆活塞磨损(BRPW),为分析其故障演变机理,建立火炮反后坐装置的后坐运动及复进运动的数学模型。
1.2 建立运动过程数学模型
1.2.1 后坐运动分析
火炮射击后,后坐部分在反后坐装置和炮膛合力的共同作用下完成后坐运动。后坐运动时火炮后坐部分的受力如图2所示。图2中,mh为后坐部分质量,g为重力加速度,Fpt为炮膛合力,Fφh为制退机力,φ为火炮高低射角,F为密封装置摩擦力,Ff1为复进机力(后坐时期),FN1、FN2为摇架导轨的法向反力,FT1、FT2为摇架导轨的法向反力相对应的摩擦力。
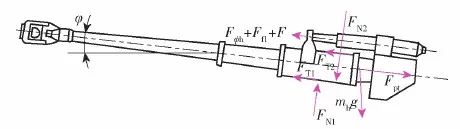
图2 后坐部分受力情况(后坐运动)Fig.2 Force analysis of the recoil part (recoiling)
根据图2所示的后坐部分受力情况,建立火炮后坐运动时的微分方程组为
(1)
式中:X为后坐位移;v为后坐速度。Fφh、FT和Ff1由式(2)得到
(2)
式中:K、K1为主流和支流液压阻力系数;ρ为制退液的密度;A0为大活塞杆活塞面积;AP为节制环孔面积;ax为变截面流液孔面积;Afj为小活塞杆内腔面积;A1为支流最小流液面积;f为摇架导轨摩擦系数;vf为游动活塞摩擦系数;V0为复进机气体初体积;Pf0为复进机气体初压;n为气体多变指数。
1.2.2 复进运动分析
火炮的后坐运动结束后,在复进机作用下后坐部分恢复到原始位置,复进过程中火炮后坐部分的受力如图3所示。图3中,Ff2为复进机力(复进运动),Fφfy为复进液压阻力。

图3 后坐部分受力情况(复进运动)Fig.3 Force analysis of the recoil part (counter-recoiling)
根据图3所示后坐部分受力情况,建立火炮复进运动时的微分方程组为
(3)
式中:ξ为复进位移;U为复进速度。Ff2、FTT、Fφf和Fφfj由式(4)得到
(4)
式中:af为节制液流孔面积;K1f为流过节制杆与节制环间隙的液体阻力系数;K2f为阻力系数。
1.3 求解运动方程数学模型
式(1)、式(3)应用4阶龙格-库塔方法进行求解,在数学分析软件中使用ode45函数实现[5]。将求解得到的后坐和复进运动过程在同一坐标系中表示,得到反后坐装置的时间-速度关系图、时间-位移关系图,如图4所示。

图4 后坐和复进运动过程中位移与速度变化Fig.4 Displacement and velocity curves during recoiling and counter-recoiling motion
如图4(a)所示,后坐过程中反后坐装置的后坐速度随着时间逐渐增加,达到后坐最大速度后逐渐开始减速,当后坐速度趋近于0 m/s时,后坐过程结束;在复进机作用下,反后坐装置开始进行复进运动,复进过程中反后坐装置的复进速度随着时间逐渐增大,达到复进到位速度后逐渐开始减速,直至反后坐装置恢复到原始位置,此时反后坐速度记为复进到位速度,复进过程结束。如图4(b)所示,后坐过程中反后坐装置的位移随着时间逐渐增加,直至后坐过程结束时达到最大后坐位移;在复进机作用下,反后坐装置开始进行复进运动,以后坐结束位置为位移零点,复进位移逐渐发生变化,直至反后坐装置恢复到原始位置,复进过程结束。
1.4 确定反后坐装置的故障特性信号
火炮反后坐装置工作时拥有两种动作状态,即射击时的后坐运动与射击完成后的复进运动,基于火炮反后坐装置运动数学模型,分别绘制反后坐装置正常状态与WTR、GLR、BRPW 3种故障状态的时间-位移曲线与时间-速度曲线,如图5所示。
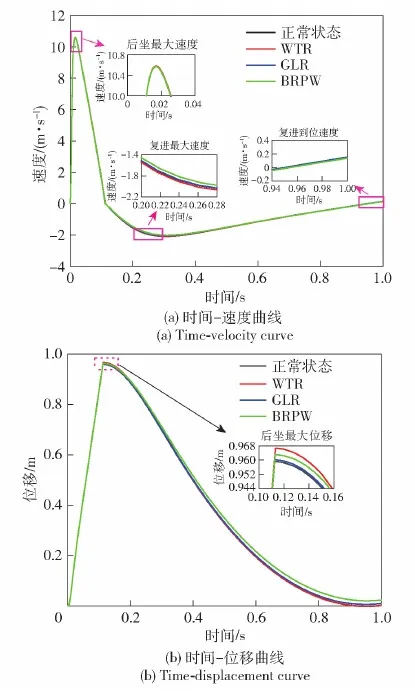
图5 不同状态下后坐复进运动中位移和速度变化Fig.5 Displacement and velocity curves during recoiling and counter-recoiling motion in different states
观察图5(a)和图5(b)可以发现,反后坐装置在处于正常状态和不同故障状态时,时间-位移曲线、时间-速度曲线的变化趋势基本一致,而后坐最大位移、后坐最大速度、复进最大速度及复进到位速度4项指标的数据大小有着较为明显的差异,因此将上述4项指标定义为火炮反后坐装置的故障特性指标,后续通过分析特征指标信号开展相应的故障诊断工作。
2 反后坐装置故障诊断方法
反后坐装置的故障特征信号可表征反后坐装的故障状态。反后坐装置的故障特性信号有后坐最大位移Xmax、后坐最大速度vmax、复进最大速度Umax及复进到位速度Uend,典型故障状态有WTR、GLR和BRPW。所提反后坐故障诊断方法共分4个阶段,整体流程如图6所示。
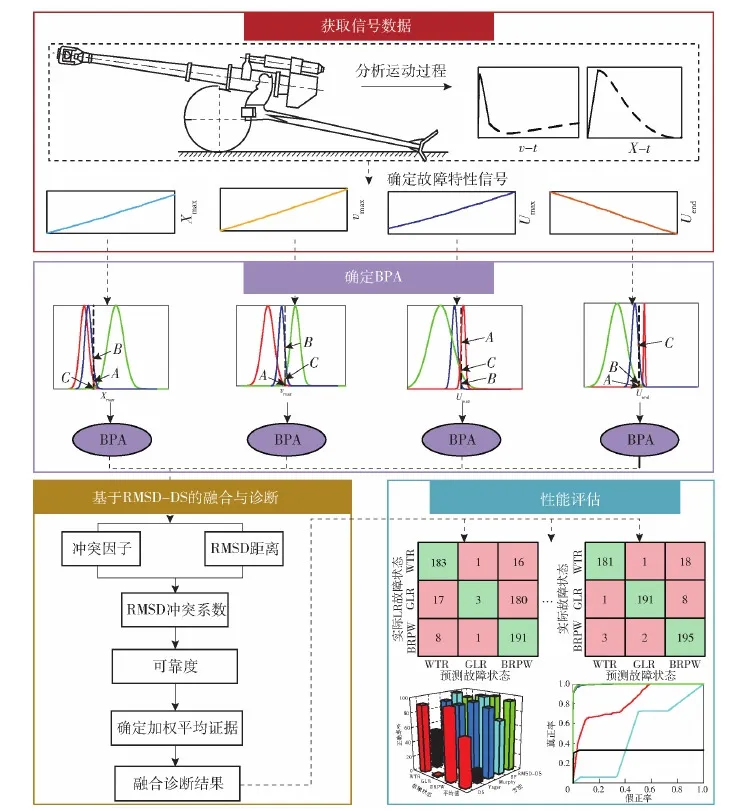
图6 故障诊断方法流程图Fig.6 Flow chart of the fault diagnosis method
由图6可见,反后坐装置故障诊断方法包括4个阶段。第1阶段为获取信号:分别收集火炮每次射击过程中反后坐装置的后坐最大位移Xmax、后坐最大速度vmax、复进最大速度Umax及复进到位速度Uend,将上述4类信号作为故障特征信号源;第2阶段为确定BPA,通过高斯模型求解每个特征信号所对应证据的BPA;第3阶段为融合与诊断,应用RMSD-DS方法融合多个特性信号所对应的证据,得到最后的融合与诊断结果;第4阶段为方法的性能评估,通过正确率、受试者工作特征(ROC) 曲线等工具对所提方法的诊断性能作出评价,并与其他代表性方法比对优劣。
2.1 数据的获取
火炮反后坐装置上布置有位移传感器、速度传感器,每次射击过程中传感器采集反后坐装置的位移与速度信号,然后分别提取位移信号中的后坐最大位移、速度信号中的后坐最大速度、复进最大速度与复进到位速度4项特征指标作为一组故障特性信号;按照同样的方法,在多次射击过程中采集多组位移与速度信号中的特征指标,最终获取反后坐装置的故障特性信号。
火炮反后坐装置在每种故障状态下有4种故障特性信号数据,所获取的单个数据用Fp,q表示,p=WTR,GLR,BRPW,分别表示3种故障状态,q=1, 2, 3, 4分别表示最大后坐位移Xmax、最大后坐速度vmax、最大复进速度Umax和复进到位速度Uend4种故障特征信号。一组样本数据为(Fp,1,Fp,2,Fp,3,Fp,4),Fp,1表示故障模式p对应的最大后坐位移数据,同理可分析得到Fp,2、Fp,3和Fp,4的含义。
2.2 基于高斯模型的BPA求解
火炮所处的变工况环境复杂多变,导致火炮反后坐装置传感器所收集的信号具有模糊性,如何有效处理信号中的模糊性对于后续的诊断工作起着至关重要的作用。模糊理论中的高斯模型基于中心极限定理,将所测量信息的概率密度函数近似描述为高斯分布,可有效反映信息的模糊性,实现信号模糊化的定量化表征[6]。因此,本文通过高斯模型求解每个故障特征信号所对应证据的BPA。
2.2.1 训练样本数据与待检样本数据的划分
获取反后坐装置的故障特性信号数据后,根据预设比例将所得数据划分为两部分,分别为训练样本数据与待检样本数据;训练样本用于构建高斯模型,待检样本作为测试样本,求解相应的BPA。
2.2.2 基于训练样本数据构建高斯模型
每种故障状态对应4种故障特性信号,因此构建每种故障状态在不同故障特征信号上所对应的高斯模型,其隶属度函数表示为
(5)
式中:μ(Fp,q)表示均值,σ(Fp,q)表示标准差,
(6)
(7)
l表示训练样本数据序列,l=1, 2, …,N。
2.2.3 求解待检样本中故障特性信号所对应证据的BPA
对于故障状态未知的一组待检样本,对应的数据可表示为(Fp,1,Fp,2,Fp,3,Fp,4),将待检样本数据与各个特征信号上的高斯模型匹配,其交点纵坐标代表该待检样本与各个故障状态在不同故障特性信号上的匹配程度,即支持程度。待检样本与各个故障状态在不同故障特性信号上的匹配程度示意图如图7所示。
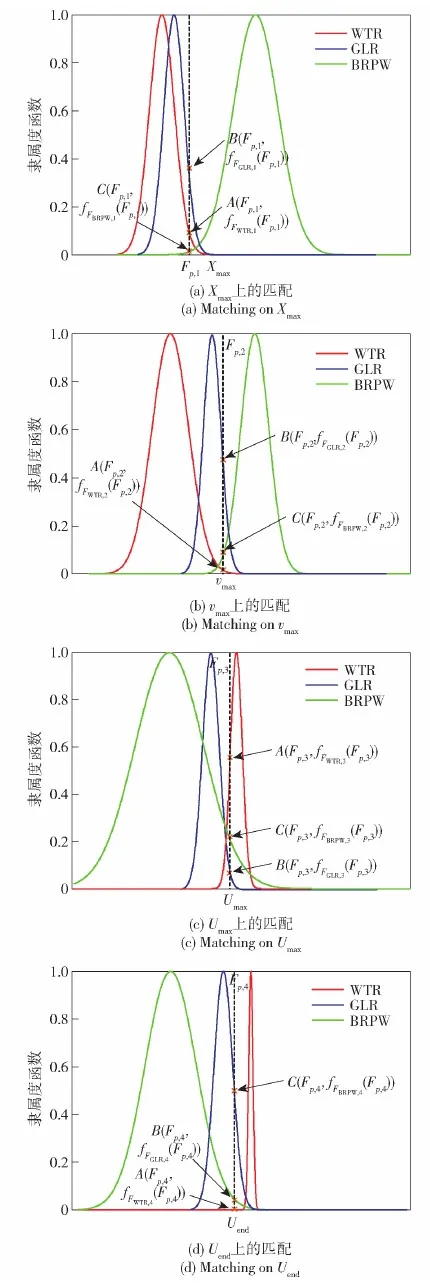
图7 不同故障特性信号上的匹配程度Fig.7 Matching degree on signals with different fault characteristics
基于图7,可求解得到各个故障状态在不同故障特性信号上的匹配程度,各个故障状态在故障特性信号为Xmax上的匹配程度求解公式为
(8)
(9)
(10)
同理可求解得到各个故障状态在其他故障特征信号上的匹配程度,匹配程度代表支持程度。每种故障特征信号下,求解所得的各个故障状态支持程度应满足加权和为1,因此对已求的支持程度进行归一化处理,所得值为故障特征信号所对应证据的BPA,以Xmax为例,给出求解公式:
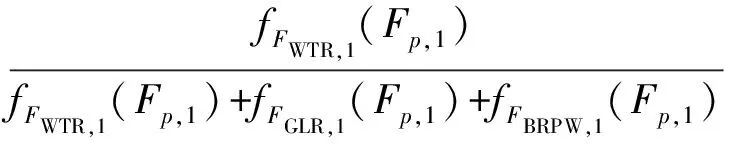
(11)
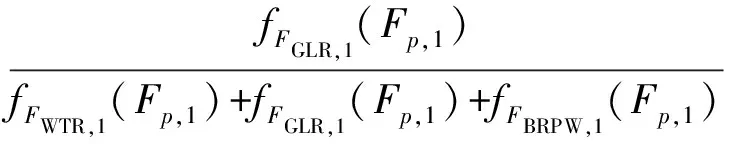
(12)

(13)
同理可求解得到其他故障特征信号所对应证据的BPA。
2.3 基于RMSD-DS的融合与诊断
2.3.1 DS证据理论
DS证据理论是一种多源信息融合方法。DS证据理论主要包括3部分,分别为辨识框架、BPA和DS融合规则。
2.3.1.1 辨识框架
辨识框架Θ是一个包含所有火炮反后坐装置故障状态类型的集合,可表示为Θ={θ1,θ2,…,θn}。
2.3.1.2 BPA函数
设辨识框架为Θ,识别框架Θ的所有子集A构成集合2Θ,识别框架Θ上的BPA函数为m∶2Θ→[0,1],满足以下条件:
(14)
2.3.1.3 DS组合规则
同一辨识框架下,两个证据m1和m2的焦元分别为(A1,A2, …,Ak)和(B1,B2, …,Br),则DS融合规则为
(15)
式中:K12为两个证据间的冲突因子,表示两个证据间的冲突程度,
(16)
DS融合规则满足交换律和结合律,因此可进一步拓展求解多个证据的合成结果。下面给出融合实例。火炮反后坐装置典型故障状态模式为WTR、GLR、BRPW,假设火炮反后坐装置的3个故障特性信号所对应的证据为m1、m2和m3,3个证据的BPA为m1∶m1(WTR)=0.1,m1(GLR)=0.9,m1(BRPW)=0,m2∶m2(WTR)=0.1,m2(GLR)=0,m2(BRPW)=0.9,m3∶m3(WTR)=0.1,m3(GLR)=0.8,m3(BRPW)=0.1。
应用DS组合规则对上述3个证据融合后,得到最终的融合结果为mfinal(WTR)=1.0、mfinal(GLR)=0、mfinal(BRPW)=0,融合结果显示支持WTR发生。然而观察各证据的BPA可知,证据m1和m3支持GLR发生,证据m2支持BRPW发生,无任何一条证据支持WTR发生,但最终的融合结果却支持WTR发生,融合结果显然产生悖论。分析可知,融合带有冲突性质的证据是造成融合结果违背常理的主要原因,在上述例子中,不同证据支持不同目标发生,导致证据之间存在高度冲突性。
火炮在作战环境中,工况复杂且易受到敌方干扰,可能会存在传感器故障或传感器错误传输数据的情况,导致不同故障特征信号所对应的证据产生高度冲突;若直接融合带有高度冲突性的证据,则可能会导致实例中所述的悖论现象发生,给反后坐装置的故障诊断工作带来困难。
2.3.2 RMSD-DS方法
解决上述问题的关键在于降低证据之间的冲突性,降低冲突性的步骤可通过给每个证据分配权重的方式来实现。通过计算每个证据在融合过程中的重要性,赋予相对应的权重,然后融合不同权重的证据,进而降低证据间的冲突性,提高融合的稳健性。基于此,提出一种RMDS-DS方法用于火炮反后坐装置的故障诊断工作中。该方法通过构造RMSD冲突系数、求解证据重要度、确定加权证据和求解融合结果等步骤组成。
2.3.2.1 构造RMSD冲突系数
DS证据理论中用冲突因子K衡量证据间的冲突程度(见式(16)),但根据式(16)求解两个一致证据的冲突因子所得值并不为0,可见冲突因子无法合理衡量证据间的冲突程度。因此,引入均方根偏移(RMSD)距离[20]修正冲突因子,构造RMSD冲突系数衡量证据间的冲突程度。
RMSD距离为相似性度量工具,两对象之间的RMSD距离越大,则代表两对象相似度低,冲突程度大;反之亦然;且两对象一致时,RMSD距离为0;可见RMSD距离和冲突因子所表述的物理意义相似。因此,以证据间冲突因子与RMSD距离(归一化)的几何均值构造RMSD冲突系数,衡量证据间的冲突程度。
定义1同一辨识框架下,两个证据m1和m2的焦元分别为(A1,A2, …,Ak)和(B1,B2, …,Bk),则两证据间的RMSD距离为
(17)
存在n个证据时,根据式(17)求解得到n个证据间的距离矩阵为
(18)
对矩阵D作归一化处理,寻求D中最大值,然后用矩阵D的每个元素除以最大值,得到归一化后的RMSD距离矩阵为
(19)
定义2同一辨识框架下,存在n个证据,两证据m1和m2的RMSD冲突系数为两证据间冲突因子与归一化后RMSD距离的几何均值,求解公式为
(20)
RMSD冲突系数衡量证据之间的冲突程度,根据式(20)求解得到n个证据间的RMSD冲突系数矩阵为
(21)
2.3.2.2 求解每个证据的重要度
定义3同一辨识框架下,存在n个证据,则证据mi(i=1, 2, …,n)的重要度为
(22)
式中:Sim(mi,mj)为证据mi与mj的相似度,
Sim(mi,mj)=1-Conij
(23)
每个证据的重要度代表该证据在融合过程中所体现的重要程度,即该证据被其他证据所支持的程度。证据的可靠度越大,表明该证据在融合决策过程中重要程度高,应该分配较多的权重;证据的可靠度越小,表明该证据在融合决策过程中重要程度低,应该分配较少的权重,以此降低证据间的冲突性。
2.3.2.3 求解与诊断融合结果
求解证据mi的权重系数为
(24)
给每个证据乘以相应的权重系数,通过加权平均求解得到新证据为
(25)
应用DS组合规则对求解得到的新证据自身融合n-1次,得到最终的融合结果。
根据上述步骤得到每个故障特性信号所对应证据的BPA,其中BPA最大值所对应的故障状态即为最终的诊断结果。
2.4 评估方法性能
诊断方法的性能可采用诊断正确率及ROC曲线来进行评估,其中ROC曲线以真正率TPR为纵坐标,假正率FPR为横坐标绘制曲线来描述故障诊断中敏感性和特异性的变化关系,能更全面系统的评估方法性能,ROC曲线下面积(AUC)越大,表明该方法的诊断性能越好[21-22]。
ROC曲线用于二分类问题,以火炮反后坐装置的WTR故障状态为例,二分类问题中WTR为阳性,其余故障统一为阴性。此时分类诊断结果会出现4类,分别为:
真阳性TP:分类诊断为WTR故障状态,实际也为节制环磨损故障状态;
假阳性FP:分类诊断为WTR故障状态,实际为其余故障状态;
真阴性TN:分类为其余故障状态,实际也为其余故障状态;
假阴性FN:分类为其余故障状态,实际为WTR故障状态。
分析火炮反后坐装置其他故障状态时,理解同上。
ROC曲线的纵坐标为TPR,又称敏感度,
(26)
ROC曲线的横坐标为FPR,又称特异度,
(27)
3 案例分析
为验证所提方法的有效性,给出数值案例和火炮案例对所提方法进行验证。
3.1 数值案例
假设m1、m2、m3、m4为4个不同信号源所对应的证据体,识别框架为Θ={A,B,C},给出证据的BPA为m1∶m1(A)=0.50,m1(B)=0.20,m1(C)=0.30,m2∶m2(A)=0,m2(B)=0.90,m2(C)=0.10,m3∶m3(A)=0.55,m3(B)=0.10,m3(C)=0.35,m4∶m4(A)=0.55,m4(B)=0.10,m4(C)=0.35。对比可知,证据体m1、m3、m4均支持识别的目标为A,证据体m2支持识别的目标为B。因此,证据体m2与其他证据存在冲突。应用本文所提方法进行融合求解,并与Deng方法、Yanger方法和Murphy方法进行对比,不同方法融合的结果如表1所示。

表1 不同方法融合结果Table 1 Fusion results of different methods
为显示不同方法的差异性,根据表1绘制应用不同方法的融合结果,如图8所示。

图8 不同方法的融合结果Fig.8 Fusion results of different methods
根据表1和图8可知,随着融合证据数量的增多,DS方法的融合结果中m(A)始终为0,表明DS方法无法有效解决冲突问题。Yager方法的融合结果中出现了未知项O,未知项实质为证据间的冲突因子;未知项的出现给最终结果的判定大大增加了不确定性,且随着融合证据的数量增多,m(A)仍始终为0,表明Yagrer方法无法解决冲突问题。Murphy方法和RMSD-DS方法中,m(A)的值随着证据数量的增加而变大,但是Murphy方法在融合4条证据后才能正确识别目标,而本文所提RMSD-DS方法在融合3个证据时便可准确识别目标,有着更强的收敛性。分析可知,本文所提方法充分考虑每个证据在融合决策过程中的重要性,根据证据的重要性对每个证据分配权重,导致所提方法的融合结果收敛速度更快,能更快速地识别和支持目标,可有效降低证据冲突对融合结果的影响。
3.2 火炮反后坐装置的故障诊断案例
3.2.1 数据来源
试验条件允许时,可根据2.1节所述火炮各类传感器获得火炮射击数据;然而在实际情况中试验条件限制难以获取真实数据,因此为验证所提方法有效性,本文基于仿真数据开展火炮反后坐装置故障诊断研究,仿真数据由式(1)~式(4)求解得到。
3.2.1.1 仿真思路
火炮反后坐装置故障诊断的大致流程为通过分析反后坐装置的故障特性信号来判定反后坐装置的故障状态。因此,需仿真得到每种故障状态下所属的4种故障特性信号;基于1.2节火炮反后坐装置运动数学模型,求解节制环磨损量Ap变化(WTR故障状态)、复进机漏气量pf0变化(GLR故障状态)及制退杆活塞磨损量A0变化(BRPW故障状态)时,与之相对应的火炮反后坐装置最大后坐位移、最大后坐速度、最大复进速度和复进到位速度数据。然后将不同故障状态所对应的故障特征信号作为故障诊断方法的原始输入数据,开展诊断工作。
3.2.1.2 故障数据的生成
WTR故障数据:假设复进机漏气量pf0及制退杆活塞磨损量A0取值为0,每次射击后节制环磨损量Ap为随机值,在满足节制环累积磨损量不超过500 mm2的条件下随机生成1 000个数据来模拟节制环故障数据;据此求解得到WTR故障状态相对应的最大后坐位移、最大后坐速度、最大复进速度和复进到位速度数据。
GLR故障数据:假设节制环磨损量Ap及制退杆活塞磨损量A0取值为0,每次射击后复进机漏气量pf0为随机值,在满足复进机累积漏气量不超过 0.2 MPa 的条件下随机生成1 000个数据来模拟复进机故障数据;据此求解得到复进机故障状态相对应的最大后坐位移、最大后坐速度、最大复进速度和复进到位速度数据。
BRPW故障数据:假设节制环磨损量Ap及复进机漏气量pf0取值为0,每次射击后制退杆活塞磨损量A0为随机值,在满足制退杆活塞磨损量不超过500 mm2的条件下随机生成1 000个数据来模拟制退杆活塞故障数据;据此求解得到BRPW故障状态相对应的最大后坐位移、最大后坐速度、最大复进速度和复进到位速度数据。
仿真所得火炮反后坐装置3种故障状态所对应的4种故障特征信号数据如图9所示。

图9 不同故障状态所对应的故障特征信号数据Fig.9 Fault feature signal corresponding to different fault states
3.2.2 故障诊断案例
确定火炮反后坐装置的典型故障状态为WTR、GLR、BRPW,将辨识框架表示为{WTR, GLR, BRPW}。
确定火炮反后坐装置的故障特性信号数据:最大后坐位移Xmax、最大后坐速度vmax、最大复进速度Umax和复进到位速度Uend。
基于3.2.1节,在火炮反后坐装置的每种故障状态下各仿真得到1 000组故障特征信号数据(每组中包含4类数据,分别为Xmax、vmax、Umax及Uend),共3 000组数据;在每种故障状态下随机选取800组故障特性信号数据作为故障训练样本数据,共 2 400 组数据;将每种故障状态中剩余200组数据作为故障待检样本数据,共600组数据。其中,模拟训练样本数据中的最大后坐位移数据受到干扰;实现步骤为将训练样本数据中的GLR与BRPW所对应的最大后坐位移数据进行调换,此步骤目的是模拟不同故障特性信号之间所对应的证据之间存在高度冲突。
根据故障训练样本数据建立不同故障状态在不同故障特性信号上的高斯模型,所求高斯模型的平均值和标准差如表2所示。

表2 高斯模型的平均值和标准差Table 2 Mean and standard deviations of the Gaussian model
根据表2所求的高斯模型如图10所示。
基与所得高斯模型,求解600待检样本数据(3种故障状态,每种故障状态有200组待检样本数据)与高斯模型的匹配程度,根据2.2节~2.3节方法求解每个特征信号所对应的证据及融合结果,得到最终的诊断结果,并与DS方法、Yager方法、Murphy方法以及BP神经网络方法进行对比,将各种方法的诊断结果以混淆矩阵形式展现,如图11所示。
混淆矩阵每一行总和代表该类别的实际样本数量,每一列之和代表被预测为该类别的样本数量。以图11(a)为例解释混淆矩阵中每个数字所代表的含义,在图11(a)中,第1行第1列的183代表真实数据类别为WTR,诊断结果为WTR的数据有 183个;第1行第2列的1代表真实数据类别为WTR,诊断结果为GLR的数据有1个;第1行第3列的16代表真实数据类别为WTR、诊断结果为BRPW的数据有16个;同理可得每行每列数值的解释。根据 图11 所示的混淆矩阵,求解得到不同方法对不同故障状态的诊断正确率和平均正确率,结果如表3所示,可视化结果如图12所示。
根据表3可知,DS方法对3种反后坐装置故障状态(WTR、GLR和BRPW)的识别正确率分别达到91.5%、1.5%和95.5%,平均识别正确率为62.8%;Yager方法对3种反后坐装置故障状态(WTR、GLR和BRPW)的识别正确率分别为53.5%、0%和0%,平均识别正确率17.8%;Murphy方法对3种反后坐装置故障状态(WTR、GLR和BRPW)的识别正确率分别达到91.0%、89.0%和96.0%,平均识别正确率为92.0%;BP方法对3种反后坐装置故障状态(WTR、GLR和BRPW)的识别正确率分别达到99.5%、17.5%和100%,平均识别正确率为72.3%;RMSD-DS方法对3种反后坐装置故障状态(WTR、GLR和BRPW)的识别正确率分别达到90.5%、95.5%和97.5%,平均识别正确率为94.5%。这些定量比较结果证明在火炮反后坐装置故障诊断中,本文所提的RMSD-DS方法优于其他方法。
分析可知:DS方法、BP方法未考虑证据间的冲突性,从而限制它们对火炮反后坐装置故障状态的识别能力;Yager方法虽然从改变DS组合规则的途径处理证据间的冲突性,但是Yager方法将证据间的冲突量划分为新的未知状态,导致Yager方法对 3种故障状态的识别正确率非常低。Murphy方法及本文所提的RMSD-DS方法的识别正确率较为理想,是因为它们对证据进行权重分配,有效降低了证据冲突所带来的影响;不过Murphy方法未考虑每个证据在融合过程中的重要性,仅是对每个证据进行了简单平均,而所提RMSD-DS方法构造RMSD冲突系数并求解每个证据的重要度,根据所求证据的重要度定量表征每个证据在融合过程中的重要程度,依据重要程度对证据赋予更加合理的权重,因此RMSD-DS方法的正确率最高。与DS方法、Yager方法、Murphy方法和BP方法相比,本文所提RMSD-DS方法正确率分别高31.7%、76.7%、2.5%和22.2%。
除正确率以外,ROC曲线也常用于评估方法性能,且可以更全面系统地对方法作出评估。绘制DS方法、Yager方法、Murphy方法以及BP神经网络方法的ROC曲线,并求解AUC,结果如图13所示。
由图13可见,DS方法的AUC值为0.827 4,Yager方法的AUC值为0.333 1,Murphy方法的AUC值为0.996 2,BP方法的AUC值为0.483 3,本文所提RMSD-DS方法的AUC值为0.997 3,与DS方法、Yager方法、Murphy方法和BP方法相比,本文所提RMSD-DS方法的AUC值分别高0.169 9、0.664 2、0.001 1和0.514 0,表明本文所提方法分类效果更佳、鲁棒性更强、诊断性能最优。

图10 不同故障特征信号上所属的高斯模型Fig.10 Gaussian models belonging to different fault feature signals
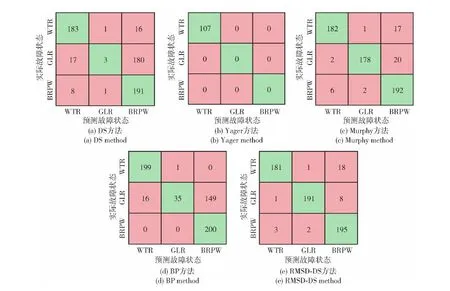
图11 不同方法的诊断结果(混淆矩阵)Fig.11 Diagnostic results of different methods (confusion matrix)

表3 不同方法的故障诊断正确率

图12 不同方法的对比Fig.12 Comparison of different methods
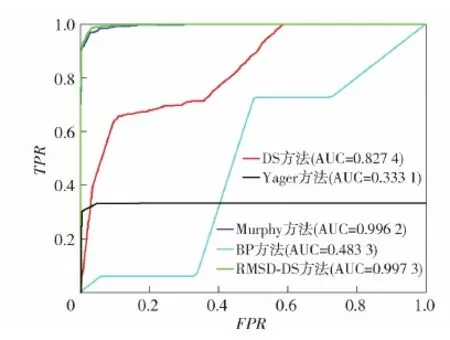
图13 不同方法的ROC曲线Fig.13 ROC curves of the five methods
4 结论
本文提出一种基于多高斯模型和RMSD-DS的火炮反后坐装置故障诊断方法,通过高斯模型获取故障特性信号所对应证据的BPA,然后应用RMSD-DS方法对所获取的BPA进行融合,有效降低证据之间的冲突影响,实现了火炮反后坐装置的故障诊断。所得主要结论如下:
1)针对变工况环境中火炮反后坐装置信号的模糊性特点,引入高斯模型确定每个故障特性信号(Xmax、vmax、Umax和Uend)所对应证据的BPA,实现信号模糊性的定量表征,且求解过程简易可靠,更契合火炮反后坐装置的实际工况。
2)针对DS方法融合高度冲突证据时出现悖论的情况,提出RMSD-DS方法。该方法通过构造RMSD冲突系数、定义重要度、为证据分配权重、求解加权证据等一系列步骤有效降低了证据间冲突性给融合所带来的不利影响。所提RMSD-DS方法与DS方法、Yager方法、Murphy方法和BP方法相比,故障状态诊断正确率分别高31.7%、76.7%、2.5%和22.2%,AUC值分别高0.169 9、0.664 2、0.001 1和0.514 0,表明所提方法的诊断性能最优。
3)基于高斯模型和RMSD-DS的诊断方法,有效处理和考虑了装备所处变工况作战环境中信号的模糊性及信号受到干扰后的冲突性,有着较强的鲁棒性,可推广应用至其他武器装备的故障诊断工作中。

