基于支持向量回归模型的弹用冲压发动机性能预测及优化
张宁, 史金光, 王中原, 赵新新
(南京理工大学能源与动力工程学院, 江苏 南京 210094)
0 引言
将炮弹与固体燃料冲压发动机相结合,可有效提高其射程,最大增程率可达70%,因此冲压增程炮弹受到诸多国家的重视。对冲压增程炮弹的研究始于20世纪70年代初期,此后美国、瑞典、南非、以色列等国家在冲压增程理论及实验方面取得了一些进展,提出了多种弹形结构,并就其空气动力学及发动机燃烧特性开展了大量研究。文献[1]首先对75 mm旋转冲压增程稳定弹进行了研究,该弹采用皮托式进气道,初速马赫数为4.3,射程为12 km,实现了自点火和稳定飞行,其后又研制出了采用中心体进气道的203 mm尾翼稳定弹,射程为60 km。文献[2]进行了40 mm冲压助推防空炮弹的研究,该弹的速度马赫数约为4.3,燃烧时间约为2~3 s。文献[3]开展了 155 mm 冲压增程炮弹的实弹射击,初速为 900 m/s,射程约为55 km。文献[4]成功完成了使用冲压发动机维持炮弹速度的飞行实验。但这些研究大多都建立在旋转弹的基础上,提高射程的同时将会降低射击精度[5],且也难以调整炮弹的飞行速度、高度与姿态,不能控制其飞行弹道。为解决上述问题,文献[6]采用简易控制技术研制了155 mm冲压增程制导炮弹,该炮弹头部有控制翼,尾部有可展开尾翼,最大巡航速度马赫数约为3,射程可达100 km,但加装控制机构会进一步压缩冲压炮弹的内部空间,减小冲压发动机体积,这将使发动机内燃气速度增加、停留时间缩短,导致发动机推力、比冲和燃烧效率下降等问题[7]。
因此,有必要在考虑弹体几何约束的情况下,优化冲压发动机结构,提高其工作性能。目前使用的优化方法主要有两种,一种是基于梯度的方法,另一种是启发式算法。为了处理多目标优化问题,前者需要通过一系列目标权重组合来定义全局目标函数[8],这种方法对假定的权重系数非常敏感,如果选择了不合适的权重,可能会丢失一些最优解。对于后者,目前使用最广泛的方法是带精英策略的非支配排序遗传算法(NSGA-Ⅱ)[9],其具有计算速度快、解集收敛性好和能在单次优化中生成帕累托前沿的优点。
但在优化过程中,计算流体力学(CFD)求解器通常必须被大量调用才能获得最优的解决方案,带来优化难度大、时间长等问题。于是,代理模型方法应运而生,并逐步受到重视,其基本思想是用一个简单的逼近函数近似替代高精度求解器。较常用的代理模型有响应面[10]、径向基函数[11]、人工神经网络[12]和Kriging[13]等方法,虽然它们都具有较好的预测能力,但为了获得较高的精度和泛化能力,必须使用大量的训练样本,从而削弱了代理模型的优势。支持向量回归(SVR)模型[14]是基于结构最小化原则的一种机器学习方法,其核心思想是,基于Mercer核展开定理,将样本空间映射到Hilbert空间中,并在其中应用线性方法来解决非线性回归问题,保证了良好的泛化能力。因此,其在解决小样本、非线性及高维问题中表现出了诸多优势[15]。
同时,由于冲压增程制导炮弹体积较小,为了保证炮弹的威力、稳定性和操纵性,通常仅能给发动机提供有限的安装空间,限制了其长度、内径和最大进气面积等结构参数。因此,本文提出了一种与弹内有限空间适配的发动机性能预测及优化方法,即基于带转捩的剪切应力输运(TransitionSST)和涡概念耗散(EDC)方程,建立了内弹道计算模型;而后,基于SVR方法构建了性能预测模型,并结合NSGA-Ⅱ对发动机结构进行了优化。所得结果可为弹用冲压发动机的性能预测及结构优化设计方法提供参考。
1 发动机几何模型与网格划分
1.1 几何模型
本文以某冲压增程弹为研究对象[5],图1为其常用的发动机结构[16-17],总长为600 mm,入口直径为35 mm;燃烧室、补燃室长度分别为247 mm和270 mm,装药内径为75 mm;喷管喉部直径为36 mm。

图1 弹用冲压发动机几何模型Fig.1 Structure of SFRJ for projectile
1.2 网格划分
图2为发动机的网格划分情况,在近壁面处加密以保证其附近参数的准确性。为模拟炮弹在海平面以马赫数2.5飞行的工况,发动机入口的空气质量流率为1.4 kg/s、温度为540 K,总压为1.0 MPa;喷管出口为压力出口;壁面绝热。
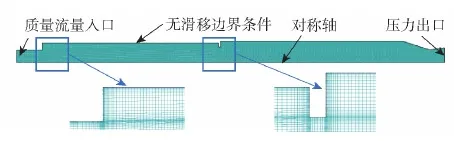
图2 冲压发动机网格Fig.2 Meshing of simulation cases
2 冲压发动机内弹道计算模型
2.1 基本假设
为简化仿真过程,获得发动机的主要工作性能,做出如下假设:
1) 燃气可近似视为理想气体;
2) 燃料内壁为气固耦合交界面,外壁为绝热壁;
3) 端羟基聚丁二烯(HTPB)推进剂的热解产物为1.3-丁二烯单质(C4H6)。
2.2 计算模型
2.2.1 控制方程与湍流模型
带化学反应的轴对称雷诺时均Navier-Stokes(N-S)方程如下:
(1)
式中:x、r分别为轴向和径向坐标;ρ为密度;p为压强;u、v分别为轴向和径向速度;μl、μt分别为分子和湍流黏性系数;Prl和Prt分别为分子和湍流普朗特数;Cp为定压热容;Cv为定容热容;T为温度;mj为组分质量分数;Rj、Dj分别为化学组分j的反应和扩散速率。
空间离散采用2阶迎风型矢通量分裂格式。由于发动机的内流场包含由尖锐几何形状引起的转捩区域[7],湍流模型选用Transition SST模型,其湍动能k以及比耗散率ω的输运方程为
(2)
(3)
式中:d为流动维数;Gk、Gω分别为湍动能和比耗散率的速度梯度;Yk和Yω分别为关于k和ω的湍流耗散项;Dω为交叉扩散项;Гk和Гω分别为关于k和ω的有效扩散系数。Transition SST模型的间歇因子和当地边界层动量厚度雷诺数输运方程见文献[18]。
2.2.2 辐射模型
本文选用离散坐标辐射模型[19]模拟发动机中的辐射传热。
2.2.3 燃烧模型
空气进入燃烧室后与C4H6发生如下化学反应[20]:
C4H6+5.5O2→4CO2+3H2O。
化学反应速率采用涡耗散模型计算。C4H6由药柱表面热解产生,因此在计算过程中,需在燃料表面与流体域交界面的第1层网格上加质。HTPB的热解速率与燃料表面温度有关,服从Arrhenius公式:
(4)
式中:A为指前因子;Ea为活化能;R为气体常数;Tw为燃料内壁温度,可由气相-固相分界面上的能量平衡方程求解[21]:
(5)
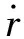

表2 C4H6主要物性参数Table 2 Main parameters of C4H6
根据文献[16-17],燃料的燃速(通常不超过1 mm/s)相较于发动机内气流速度(一般为100 m/s)较慢,因此,可忽略燃面退移对流场的影响。
2.2.4 推力与比冲、燃烧效率模型
由动量定理,发动机推力F为出口截面气流与迎面气流的冲量差,即
(6)

比冲可定义为单位质量燃料所产生的推力,即
(7)
根据文献[21],燃烧效率可定义为
(8)
式中:YCO2、YC4H6表示混合气体中各成分的质量分数;MCO2、MC4H5表示混合气体中各成分的摩尔质量;S为截面面积。
2.3 网格收敛性分析
由于在固定几何形状下,发动机的比冲仅与其推力与燃速有关,可只选取初始冲压发动机的推力、燃烧效率和平均燃速作为网格独立性检验的指标。选取网格的总数约为14、21、32、48和72万个,收敛结果如表3所示。
表3 网格收敛性分析Table 3 Grid convergence analysis
将前5个网格与108万网格的相比,发动机推力偏差分别为38.82%、20.67%、7.47%、2.78%、0.28%,燃烧效率偏差为9.16%、7.33%、3.32%、2.31%、0.97%,平均燃速偏差为14.51%、12.16%、3.99%、2.53%、0.73%。在保证精度的情况下,为了尽可能地提高计算效率,选择网格数目为72万。
3 冲压发动机工作性能优化模型
受制导炮弹结构限制,其所用的冲压发动机通常较小,同时发动机结构对其性能有极大影响[22]。例如,当发动机总长一定时燃烧室越长,则推进剂装填量越大,能产生更大的推力,但比冲较低;反之,发动机的比冲较大而推力较小[23]。因此,有必要在考虑炮弹几何约束的情况下,优化发动机结构以提高其推进性能。图3为本文建立的优化工作流程,包含预处理、内弹道计算和多目标优化3个模块。
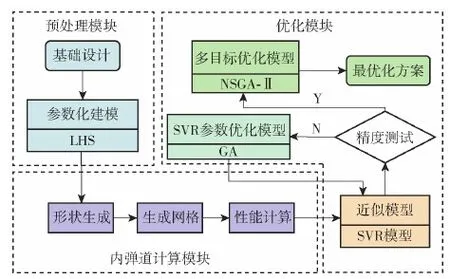
图3 冲压发动机优化流程Fig.3 Optimization workflow of theramjet
具体操作流程如下:
1) 使用拉丁超立方抽样(LHS)方法[24]在设计空间中生成训练和测试数据集。
2) 将训练和测试集中的每个样本代入内弹道模型进行计算,得到发动机的推力、比冲、燃烧效率等指标。
3) 建立SVR模型并通过测试集进行精度校验,若不满足,则对其参数进行寻优更新。
4) 基于多目标优化模型得到最终的优化解。
3.1 SVR模型
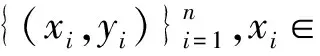
f(x)=w·φ(x)+b
(9)
式中:w、b分别为权向量和阈值;φ(x)为设计变量的组合函数,w·φ(x)为w与φ(x)的内积,并且满足结构风险最小化原理。在精度ε下,f(x)能够估计每组设计变量对应的响应值,即为所需的近似函数,其参数求解可以转化成求解凸优化问题:
(10)
(11)
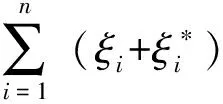
(12)
相应的预测函数变为
(13)
模型的误差可表示为
(14)
式中:Nc为测试集中的样本数目;为SVR估计响应值。若模型精度不满足要求,则可使用遗传算法对参数C、γ寻优更新。
3.2 多目标优化模型
图4为冲压发动机的几何模型,其中,L为冲压发动机总长,din为进气道入口截面的半径;hc、lc分别为燃烧室突扩台阶高度和长度;hp为隔板高度;lm、dm分别为补燃室的长度和内径;dr为尾喷管的喉部半径,ls为收敛段长度,le为扩张段长度,dout为尾喷管的出口半径,本文选用hc、lc、hp、lm、dm、dr、ls、le、dout这9个参数作为优化设计变量。
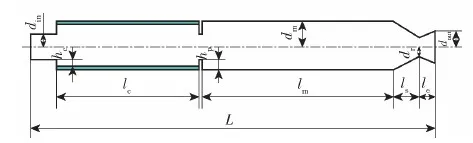
图4 冲压发动机几何模型Fig.4 Geometric model of the ramjet
在发动机性能优化过程中,除了要保证燃料的混合效率和燃烧效率外,还需要考虑弹上其余装置对空间的需求以及与进气道的适配性。例如,由于发动机的补燃室上方带有战斗部,为保证弹药威力,燃烧室和喷管的长度、补燃室内径都不宜过大。根据以上分析,冲压发动机的工作性能优化模型建立如下:
(15)
式中:kt、kI分别为推力、比冲的归一化比值;F0和I0分别为具有初始冲压发动机的推力和比冲值;Lmax为发动机最大长度;hmax为突扩台阶最大高度;dmax为补燃室最大内径。式(15)约束条件中有:设计变量的取值范围,发动机尺寸与炮弹可用空间的适用性;冲压发动机性能约束,以确保大部分燃料能量可以在发动机中释放;适配性约束,确保发动机产生的压力不会超过气道所能抵抗的最大背压pmax。
3.3 带有罚函数的NSGA-Ⅱ
由于冲压发动机工作性能优化问题是带有约束的多目标优化问题,可采用NSGA-Ⅱ[9]与罚函数相结合的方法进行求解,即将原适应度函数与Static Hoffmeister(SH)惩罚项组合,构造增广适应度函数:
(16)
(17)
式中:f0(x)为原适应度函数;ϑ为罚因子;gz(x)为第z个约束函数;H(gi(x))在满足约束条件时取0,否则取1。为了提高计算效率,根据范数相容性原理,可将式(17)改写为
fitness(x)=f0(x)+ϑH(gmax)|gmax|
(18)
式中:gmax为gi(x)的最大值。
带有罚函数的NSGA-Ⅱ算法流程如图5所示。
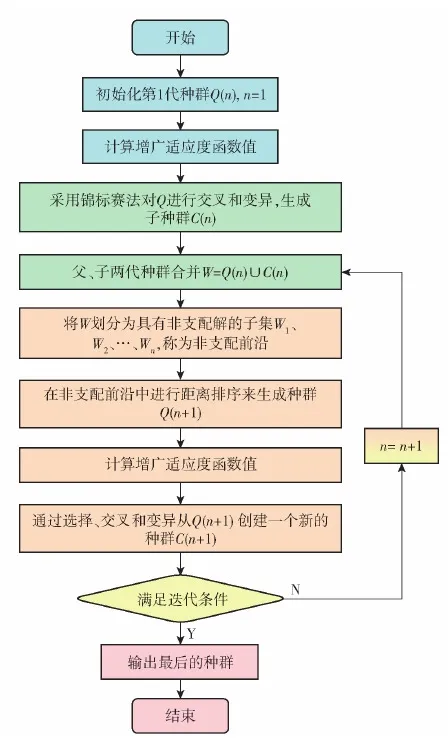
图5 带有罚函数的NSGA-Ⅱ流程Fig.5 NSGA-Ⅱ flow witha penalty function
4 数值模拟结果与分析
4.1 计算模型可靠性检验
4.1.1 内弹道计算模型可靠性验证
依照文献[25]所述方法,本文对所用的内弹道计算模型进行了可靠性验证。针对冷流实验[26],获得的燃烧室中心线轴向速度va与实验结果基本一致,如图6所示,而回流区长度较实验值约差0.98%,表明该计算模型可较好地模拟发动机内气流的流动过程。

图6 燃烧室中心轴向速度Fig.6 Mean axial velocity alongthe combustor centerline
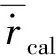

表4 计算结果与实验结果的对比Table 4 Comparison between the calculated results and experimental results
4.1.2 SVR模型可靠性验证
为检验代理模型的预测精度,采用100个样本点建立了预测模型,并使用另外40个样本点进行计算,与高精度求解器结果间的误差对比如图7所示。图7中,δt表示推力误差,δI表示比冲误差,模型预测结果的平均误差为1.24%,最大误差为2.71%,不超过3%,可靠性较好。
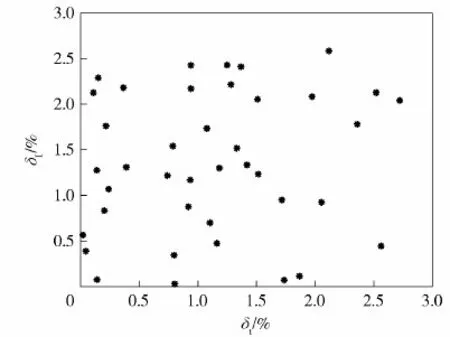
图7 预测值与计算值对比Fig.7 Comparison between predicted and calculated values
4.2 优化结果分析
图8显示了NSGA-Ⅱ获得的非支配结果,可以看到较清晰的帕累托前沿分布,比冲随着推力的增加而减小,表明在此工况下冲压发动机的优化设计必须在两个目标函数间进行折衷。
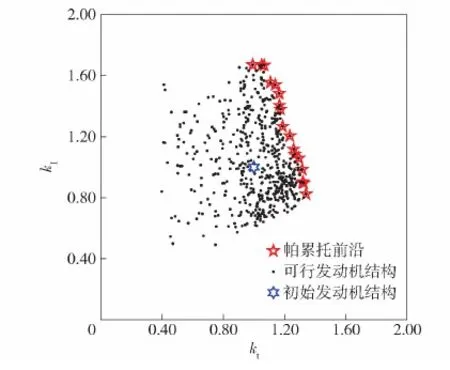
图8 冲压发动机多目标优化设计的帕累托解集Fig.8 Pareto solution set for multi-objective optimization design
因此,本文设计了一个决策函数,在解集中选择一个合适的设计点,即
M=kt+λkI
(19)
式中:λ表示权重系数,可以根据目标的重要性进行调整,在此分析中该值取为1。基于此,获得的最佳冲压发动机形状如图9所示,参数如表5所示。由图9可以发现,优化后的冲压发动机燃烧室长度减小,补燃室长度增加、内径减小,一方面可以增加燃气的掺混效果,提高发动机的燃烧效率;另一方面则可使补燃室上方战斗部的装药量增加,保证了弹药威力。
图9 λ=1时优化后的冲压发动机结构Fig.9 Optimizedramjet shape when λ=1

表5 优化后发动机结构参数
图10、图11出了优化前后冲压发动机中C4H6和O2的分布情况,可以发现,二者组分分布情况一致,C4H6都主要集中于发动机壁面附近,而氧气则主要位于发动机的中心区域,火焰层在富氧区与燃料内壁间形成,因此燃气的混合效果较差,降低了发动机的燃烧速率。因此,部分燃料将在补燃室中继续和氧气反应。但在优化后发动机尤其是补燃室内C4H6剩余较少。这是因为其补燃室更长,提高了燃料的停留时间,使其与空气反应更为充分;同时燃烧室内的湍流动能随着突扩台阶高度的增加而增大[17],提高了室内燃料与空气的掺混和燃烧效率。

图10 发动机中C4H6的质量分数Fig.10 C4H6 mass fraction of the ramjet

图11 发动机中O2的质量分数Fig.11 O2 mass fraction of the ramjet

图12 初始冲压发动机的温度和流线图Fig.12 Temperaturecontour and streamline of the initial ramjet
图12、图13给出了优化前后冲压发动机的温度和流线图。分析流线图可知,二者流动情况大致相同,但优化后,燃烧室内回流区长度增加、补燃室内回流区长度减小,这是因为其突扩台阶高度增加,补燃室内径减小,改变了原有结构的后台阶高度,从而改变了其后部漩涡的再附长度。由二者的温度图像可知,发动机优化后,其燃烧室后部和补燃室内的温度更高,这是因为其突扩台阶高度的增加,提高了燃烧室内的湍流动能,使得燃烧室内燃气掺混和燃烧效率增加,同时,其较长的补燃室保证了燃气在其中充分的燃烧,这也与图10、图11的C4H6和O2的分布情况相符。

图13 优化后冲压发动机的温度和流线图Fig.13 Temperature contour and streamline of the optimized ramjet
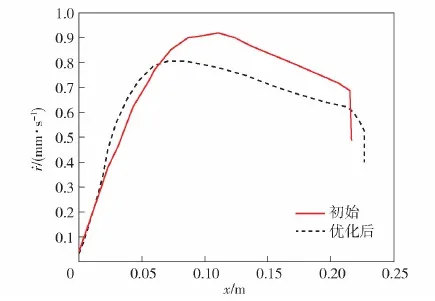
图14 燃速沿轴向分布情况Fig.14 Regression rate along grain surface
表6比较了优化前后的推力和比冲。由表6可知,优化后发动机推力提高了24.22%。由图14可知,初始冲压发动机的燃速约为0.774 mm/s,而优化冲压发动机的燃速约为0.822 mm/s。后者虽然燃速较高,但由于燃料长度缩短了13.88%,其燃料质量流量与前者相近,同时优化后燃烧效率约提高了12.02%,其比冲也提高了约20.28%。因此优化后的冲压式喷气发动机具有更好的推进性能。
5 结论
本文提出了一种与弹内有限空间适配的冲压发动机性能预测及优化方法。首先,采用Transition SST和EDC方程,建立了其内弹道计算模型,并获得了相应的流场结构与性能参数;在此基础上,基于SVR模型构建了发动机性能参数的预测模型,并与NSGA-Ⅱ结合对发动机结构进行了优化。得到以下主要结论:
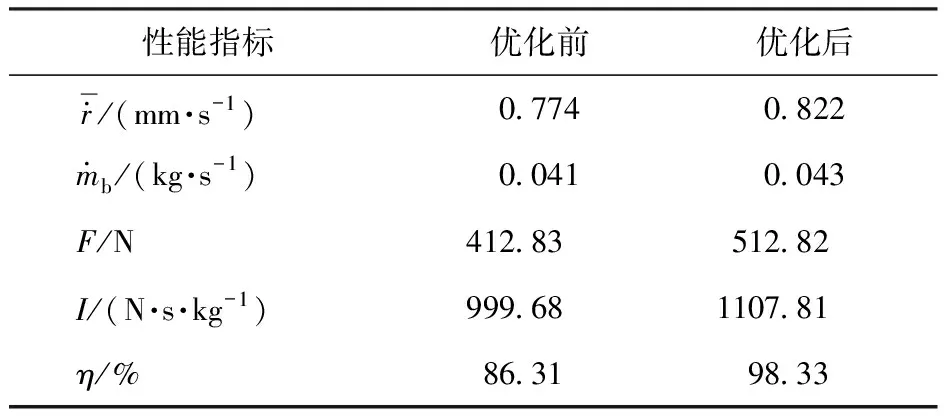
表6 优化前后发动机性能指标Table 6 Performance of the ramjet
1) 在工况相同的情况下,本文方法计算所得的燃料平均燃速,与实验结果相比,绝对误差平均值不超过1.5%,表明所用模型精度较高,能较好地模拟发动机内的燃烧与流动过程。同时,本文构建代理模型的预测结果与高可信度模型的计算结果相差较小,最大相对误差不超过3%,具有较高的精度,可以提升冲压发动机性能计算与分析的效率。
2) 优化前后流场结构与各组分分布情况大致相同,都在发动机燃烧室入口后台阶以及补燃室隔板后台阶处出现了回流区,但优化后的燃烧室内回流区更长;C4H6主要集中于燃烧室上部,而氧气主要集中分布在燃烧室通道的中心区域,但优化后的发动机尤其是补燃室内C4H6剩余较少。
3)发动机结构优化后,燃烧室缩短了13.88%,补燃室长度增加了13.50%,空气与燃料混合更充分,推力、比冲和燃烧效率分别增加了24.22%、20.28%、12.02%。利用该优化设计方法设计的发动机性能更优,为有限空间内弹用冲压发动机的设计提供了可行的方法与工具。

