不等式解法及证明复习策略

■江西省南昌市第三中学 刘红坤 杜 宽

历年高考中,不等式模块主要考查绝对值不等式的解法、绝对值三角不等式和不等式证明等。将不等式融合到其他试题中,突出了不等式的工具性,淡化了其独立性。下面我们对该模块进行分析,来理解不等式的本质,熟悉不同问题的处理策略,积累不同题型的解题经验与技巧,感悟其中蕴含的思想方法,进一步提高解题效率。

一、不等式的主要题型

1.含绝对值不等式的解法

评注:去掉绝对值的方法一般有以下几种:(1)抓零点分区间讨论;(2)平方法:利用|f(x)|＞|g(x)|⇔f2(x)＞g2(x)去绝对值;(3)几何法:利用绝对值的几何意义求解;(4)数形结合法:在直角坐标系中作出不等式两边所对应的两个函数的图像,利用函数图像求解。

2.绝对值三角不等式的应用

例2已知函数f(x)=|x-a|+|x+3|。

(1)当a=1时,解不等式f(x)≥6;

(2)若f(x)＞-a,求a的取值范围。

解析：(1)当a=1时,f(x)=|x-1|+|x+3|。

若x≤-3,则f(x)=-2x-2≥6的解为x≤-4;

若-3＜x≤1,则f(x)=4≥6无解;若x＞1,则f(x)=2x+2≥6 的解为x≥2。

综上可得,不等式f(x)≥6 的解集为{x|x≤-4或x≥2}。

(2)依题意f(x)＞-a,即|x-a|+|x+3|＞-a恒成立。

因为|x-a|+|x+3|=|a-x|+|x+3|≥|a+3|,当且仅当(a-x)(x+3)≥0时取等号,所以f(x)min=|a+3|,故|a+3|＞-a,解得。

所以a的取值范围是。

评注:运用“f(x)≤a恒成立⇔f(x)max≤a,f(x)≥a恒成立⇔f(x)min≥a”可解决恒成立中的参数取值范围问题。

3.不等式的证明

评注:证明不等式的方法灵活多样,但比较法、综合法、分析法仍是证明不等式的基本方法。要依据题目的结构特点和内在联系进行适当变形,创造条件使用重要不等式、基本不等式、柯西不等式、权方和不等式等去证明,要熟悉各种证法中的推理思维方法,并掌握相应的步骤、技巧和语言特点。

4.解绝对值不等式与证明不等式的综合

例4已知关于x的不等式|2x|+|2x-1|≤m有解。

(1)求实数m的取值范围;

(2)若a＞0,b＞0,a+b=1,证明:。

解析：(1)因为|2x|+|2x-1|≥|2x-(2x-1)|=1,当且仅当2x(2x-1)≤0,即时取等号,所以m≥1。

故实数m的取值范围为[1,+∞)。

(2)由题意知a+b=1,又因为(a+2b+2a+b)≥(a+b)2,所以。

评注:含绝对值不等式恒成立问题、存在性问题、有解问题是高考中的热门题型。该类题型常转化为求不等式的最值问题。在应用柯西不等式时,要注意等号成立的条件,柯西不等式在排列上规律明显,具有简洁、对称的美感,运用柯西不等式时,要“一观察、二构造、三判断、四运用”。

二、不等式试题中的数学思想

例5(2023 年全国甲卷第23 题)已知a＞0,函数f(x)=2|x-a|-a。

(1)求不等式f(x)＜x的解集;

(2)若曲线y=f(x)与x轴所围成的图形的面积为2,求a。

解析：(1)当x≤a时,f(x)=2a-2xa＜x,即3x＞a,解得;

当x＞a时,f(x)=2x-2a-a＜x,解得x＜3a,即a＜x＜3a。

(2)结合分段函数知f(x)=画出f(x)的草图,如图1所示,则f(x)与x轴围成△ABC,△ABC的高为a,,所以|AB|=a,所以,解得a=2。

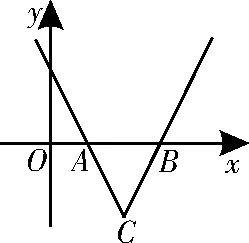
图1

评注:本题将含有绝对值的函数先表示成分段函数的形式,综合运用数形结合、分类讨论的数学思想解决问题。

在复习过程中,我们要对知识方法、数学思想归纳整理,追本溯源,提炼出通性通法所涉及的数学思想,提高运算求解能力、变形能力、数形结合能力、逻辑推理能力等,并在具体问题情境中能够加以“灵活”“综合”运用,从而提升数学素养。