基于改进指数趋近律的PMSM滑模观测器控制策略
王富利, 张 瑞, 赵 浩
(黑龙江科技大学 电气与控制工程学院,哈尔滨 150022)
0 引 言
传统的滑模观测器算法在控制永磁同步电机(permanent magnet synchronous motor, PMSM)时存在测量误差较大、抖振误差大的问题,因此,削减滑模控制过程中的抖振、减小滑模观测器的测量误差一直是研究热点[1-3]。文献[4-5]改进了指数趋近律,使用饱和函数代替不连续的切换函数,并通过模型参考自适应来对转速进行估算,但模型参考自适应法受电机本身参数影响较大,适用范围较小。文献[6]提出用一种新的饱和函数替代不连续的函数,使得观测器转子估计误差变小,但相较传统指数趋近律而言,改进较小,抖振误差仍旧较大。文献[7]将幂次趋近律与指数趋近律结合在一起,减缓了到达滑模面时系统的抖振,并应用在船舶电机控制中。文献[8]在传统指数趋近律的系数中引入系统状态变量和滑模面函数,使得系统有2种不同的速度趋近滑模,减小抖振的同时提高了收敛速度。
对传统指数趋近律进行改进,首先搭建基于指数趋近律构建的滑模观测器,然后为进一步减小稳态误差,将指数趋近律改进,提出一种系数可变的新型指数趋近律,并采用积分滑模面代替传统滑模面,以改进的趋近律为控制函数搭建新的滑模观测器。
1 PMSM数学建模
以表贴式PMSM为对象,建立静止坐标系下电流状态方程为
(1)
式中:LS、RS为定子的电感、电阻;ωe、θe为电角速度、电角度;Eα、Eβ为反电动势;φf为永磁体磁链;iα、iβ为定子电流;Uα、Uβ为定子电压;α、β为静止坐标轴。
2 改进指数趋近律
2.1 传统指数趋近律
传统指数趋近律表达式为
s=-εsgn(s)-qs
(2)
式中:ε为等速超近项系数;q为指数趋近项系数,且ε、q>0。
由于不连续函数sgn(s)的存在,会导致系统产生抖振,抖振的存在影响算法的精度,因此,提出一种新的指数趋近律,以达到削减抖振、减小误差的目的。
2.2 新型指数趋近律
由式(2)可以看出,传统指数趋近律的系数ε、q为常数,因此当系统状态发生变化时,传统指数趋近律不能很快适应系统状态的变化,从而导致控制系统跟踪的误差过大。针对这个问题,提出一种变系数的新指数趋近律,从而减小测量误差,提出的新的指数趋近律表达式为
(3)
(4)

(5)
式中:g(x1,s)为对式(2)中ε做的改进,使得ε不再是一个常数,而是一个可以随系统状态变化的量,f(s)为对式(2)中qs做的改进,使趋近滑模面的效果更好。δ,α,k,M均为常数 ,通过调节他们的量来使得g(x1,s)和f(s)达到理想的控制效果,且0<δ<1,0<α<1,k>0,0
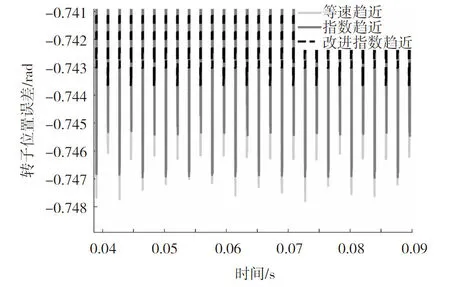
当系统距离滑模面较远时,此时g(x1,s)会趋近于k/δ,f(s)等于qs|s|^b,此时系统以这2种速度趋近滑模面,且限定了δ,b的取值范围之后,在远离滑模面时,改进的指数趋近律会比一般指数趋近律有着更快的趋近速度; 当到达滑模面附近时,因为δ的值较小,所以g(x1,s)会趋近于|x1|k/(1+|x1|),f(s)等于qs|s|^b,从而有[|x1|k/(1+|x1|)] 选取李雅普诺夫方程为 (6) 若满足可达性条件dV<0,则可说系统是稳定的,联立式(3)~(6),得到 (7) 因为限定了待设计参数k,δ,q,α,b,M的取值范围,所以式(7)是小于0的,满足可达性条件,可知改进的指数趋近律是稳定的。 滑模观测器法是PMSM无传感器控制中常用的方法,主要应用于PMSM中高速控制中。 传统滑模观测器构建的滑模面为 (8) 选取等速趋近的函数作为滑模控制函数: (9) 当系统到达滑模面之后,电流误差为零,滑模面函数为零,联立式(1)、(8)、(9)得到 (10) 将式(10)带入式(1),得到传统滑模观测器数学表达式为 (11) 为进一步减小稳态误差,利用积分滑模面代替线性滑模面构造观测器: (12) 式中:c1、c2为常系数,且c1、c2>0;eα、eβ为系统状态量,设计中取电流观测值与实际值误差为eα、eβ。 对式(12)求导从而得到滑模面导数式为 (13) 分别选取一般指数趋近律和改进后的指数趋近律作为控制函数,将式(3)改写得到改进后的指数趋近律表达式: (14) 将指数趋近律改写得到一般指数趋近律表达式: (15) 设计滑模观测器控制律为 (16) 式中:k1、k2为控制系数。 联立式(1)、(12)~(16)从而得到反电动势,改进后指数趋近律反电动势为 (17) 指数趋近律反电动势为 (18) 将式(17)、(18)带入式(1),得到滑模观测器表达式(19)、(20),式(19)为改进指数趋近律构建的滑模观测器,式(20)为一般指数趋近律构建的滑模观测器。 (19) (20) 仿真整体框图如图1所示,设置PMSM电机仿真参数见表1。 图1 整体框图 表1 仿真参数表 为验证仿真结果,将传统滑模观测器、基于指数趋近律构建的滑模观测器和基于新趋近律构建的滑模观测器的控制效果进行对比。设置永磁同步电机初始负载为0,额定转速为1 000 rad/min;在突加转矩的实验中,设置在0.05 s突加5 N的负载转矩。 3种控制策略转速跟踪误差如图2所示,可以看出,SMO最大转速稳态误差为5.5 rad/min,ISMO最大转速稳态误差为3.8 rad/min,IISMO最大转速稳态误差为0.7 rad/min,即IISMO有着最好的稳态性能。 图2 3种控制策略转速跟踪误差对比 3种控制策略转矩跟踪误差如图3和图4所示,可以看出,SMO最大转矩稳态误差为1.12 N·m,ISMO最大转矩稳态误差为0.9 N·m, IISMO最大转矩稳态误差为0.6 N·m,即IISMO的转矩跟踪误差最小。 图3 3种控制策略转矩跟踪误差对比 图4 3种控制策略转速跟踪误差对比放大图 图5 3种控制策略转子位置跟踪误差对比 3种控制策略转子位置跟踪误差如图 5和图6所示,可以看出,SMO转子位置估计最大稳态误差为0.748 rad,ISMO转子位置估计最大稳态误差为0.747 rad, IISMO转子位置估计最大稳态误差为0.743 rad。 从图2~6可以看出,ISMO相较SMO有着更好的稳态控制性能,而IISMO则在ISMO的基础上进一步提高了测算精度 ,减小了测量误差。 突加转矩时转速跟踪误差如图7所示,可以看出,SMO最大转速误差为6.1 rad/min, 最大转速稳态误差为5.5 rad/min;ISMO最大转速误差为5.4 rad/min, 最大转速稳态误差为3.8 rad/min;IISMO最大转速误差为2.5 rad/min,最大转速稳态误差为0.7 rad/min。 图7 3种控制策略转速跟踪误差对比 突加转矩时转矩跟踪误差如图8和图9所示,可以看出,SMO最大转矩稳态误差为1.12N·m,ISMO最大转矩稳态误差为0.9 N·m, IISMO最大转矩稳态误差为0.6 N·m,且转矩最大误差3种控制策略差不多。 图8 3种控制策略转矩跟踪误差对比 图9 3种控制策略转矩跟踪误差对比放大图 由此可知,突加负载时,IISMO转速误差依旧最小,突加负载稳定运行后的转矩稳态误差最小,控制性能更好,但是在转矩最大误差上IISMO较ISMO和SMO提升不明显。 从改进趋近律以减小传统滑模观测器测量误差的角度出发,提出一种系数可变的自适应指数趋近律,并以此构建IISMO,同时对SMO,ISMO,IISMO这3种控制策略进行仿真验证和比较。仿真结果表明,提出的IISMO有着更好的控制跟踪性能,测量误差更小,但在转矩最大跟踪上控制效果较SMO和ISMO提升不大,需采取新的措施改进。2.3 新型趋近律稳定性分析
3 滑模观测器的构造
3.1 传统滑模观测器的构造

3.2 改进后的滑模观测器构造



4 仿真验证


4.1 空载启动



4.2 突加负载时



5 结 语

