信息化赋能数学探究，项目式提升育人价值

周远方　张利

摘要：在“正方体截面的探究”活动中，教师采用信息化教学和项目式学习相结合的方式，合理地使用信息技术帮助学生建立数学直观，引导学生对正方体的截面特征、做法和性质进行深入探究，让学生在真实的问题情境中感悟数学本质，提升数学核心素养，可视化展示探究全过程。信息技术与数学探究深度融合，促进了信息技术的精准使用、项目教学的精细实施和探究成果的精彩展示，实现了数学探究活动的育人价值。

关键词：正方体截面；数学探究；信息技术；项目式学习；育人价值

《普通高中数学课程标准（2017年版2020年修订）》（以下简称“课程标准”）将数学探究活动与数学建模活动列为课程主题之一。数学探究活动的重要性不言而喻。但是，教师在设计与开展数学探究活动时，对教学不够重视，普遍存在实践经验不足、信息技术缺乏、示范课例较少等问题。基于此，中国教育学会中学数学教学专业委员会在第十届高中青年数学教师课例展示活动中，选取课程标准中的第11个课例“正方体截面的探究”作为指定课题，并明确给出了如下的内容要求和教学提示。

内容要求：综合利用基本立体图形的结构特征、基本图形位置关系中的结论、定理，引导学生探究、发现、证明正方体截面的形状、大小等的变化规律，积累数学探究的经验。

教学提示：这是一项数学探究活动，学生可以在一节课中完成其中的一部分，用课余时间独立完成整个探究任务，并撰写报告。教师可以重点展示课堂上的探究部分，引导学生提出问题，并根据当地条件采取不同方式进行探究。探究的难点是分类找出所有可能的截面，并证明哪些形状的截面一定存在或者一定不存在。教师应鼓励学生操作、观察，进而猜想、证明结论，在逐渐深入的探究过程中，提高发现问题、分类讨论、作图表达、推理论证等能力，在具体情境中提升直观想象、数学抽象、逻輯推理等素养，积累数学探究活动经验。

上述内容要求与教学提示，特别强调将信息技术融合到创设探究情境、开展探究活动和提炼探究方法等环节之中，体现课程标准重视信息技术应用的宗旨，有效指导了数学探究活动的实施。

在“正方体截面的探究”的同课异构中，山西省实验中学教师张永刚（执教“课例1”）和湖北省宜昌市第一中学教师李智伟（执教“课例2”）表现尤为出色。两位教师按照课程标准的要求，充分发挥信息技术直观便捷、资源丰富的优势，帮助学生发展数学核心素养，共同演绎了两节数字化探究正方体截面的范例，获得好评。有兴趣的读者可参阅课例1^[1]和课例2^[2]的教学设计。笔者结合这两个课例，介绍利用信息技术开展探究活动的方法并给予具体评价。

一、借助信息技术创设问题情境，实现项目式学习的深度探究

怎样体现数学探究活动教学的精准化、高效化和个性化？如何实现数学探究活动的教、学、评一体化？针对这些问题，在数学探究学习活动中，教师应将信息技术作为引导学生学习和探究的重要辅助手段，搭建学生、教师和技术之间相互交流的平台，为学生探究提供丰富的资源。

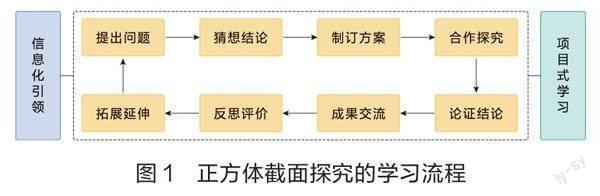
两个课例，教师十分重视信息技术与数学探究的深度融合，采用“直观感知、操作确认、推理论证、度量计算”的探究策略，开展了基于信息技术进行项目式学习的实践探究。两个探究活动非常成功，不仅设计合理、任务安排得当、探究特点鲜明，而且实施有序、展示成果丰厚、个性特点突出，展现了数字化探究正方体截面的全过程。两位教师都针对学生的探究活动设计了信息化与项目式相结合的学习流程（如图1），放手让学生独立发现问题和提出问题，借助信息技术共同分析问题和解决问题，为数学探究活动的教学提供了有效的实施路径。

课例1中，教师让学生课前用GeoGebra软件或几何画板等工具制作了“正方体的截面”课件^[3]。学生在此过程中，学会了运用计算机辅助教学（CAI）的复合、分解等手段，对图形进行分割、叠加、拼凑，使得截面变化更加形象直观。制作者利用信息技术工具动态演示，将不同图形在各种位置的变化过程淋漓尽致地演示出来，简明直观，令人印象深刻。

为帮助学生提高数学探究能力，将学生从模仿者逐步培养成为探索者，课例2中的教师实施本原性问题驱动下的探究式教学，即选取正方体截面中的本原性问题为引子，模拟数学家做数学研究的情境，让学生经历数学问题发现、分析和解决的过程，回归探究的本真。教师按“选题、开题、做题、结题”四环节组织探究活动，上课前期下发“正方体截面探究的项目学习任务单”给学生，要求学生借助信息技术思考并完成探究任务。四项探究任务分别为：截面有没有可能是直角三角形；截面有没有可能是直角梯形；截面有没有可能是正五边形；截面有没有可能是正六边形。教师将全班分成几个小组，要求各组安排时间集中研讨，完成选题和开题的活动任务，接受中期检查，完成课题。教师将学生自主探究任务置于课前，确保学生有充足的探究时间，提高了探究质量；将探究过程融入“问题链＋任务单”的情境活动中，课堂上以结题和交流为主，以信息技术辅助展示为辅，提升了探究效果。

教师设计项目学习任务单有助于学生进行可视化观察与操作，形成猜想，证明结论。探究教学的前提是如何让学生真实探究，这也是教师设计探究活动的依托。这两个课例中，教师引导学生开展项目式学习，有利于学生深度学习。

二、借助信息技术直观感知截面，实现探究途径的多样化

教师让学生借助信息技术观察正方体截面形状的动态变化过程，有助于激发学生对探究活动的兴趣。从探究方法来看，两个课例的执教者都是让学生利用信息技术工具，先操作观察，再猜想证明，最后获得结论，遵循研究一个数学对象的一般路径（事实—发现—猜想—论证），采用多样化的探究方式，尤其是融合几何画板等数字化工具对正方体截面图形进行动态呈现，引导学生探究。

信息技术与数学探究的深度融合，既可以有效减少学生的机械想象、重复运算和低阶思维现象，又能够适当增加学生的算法思想、模型思想和高级思维活动，还能够更好地帮助学生发现问题、提出猜想和验证结论。两位教师都十分注重将技术与探究有机结合，充分发挥信息技术在可视化分析截面形状、动态化呈现截面变化和直观化探究截面性质等方面不可替代的作用。

例如，在课例1中，学生利用GeoGebra软件探究，发现连接正方体各棱中点的截面正好为正六边形的情形，进而再利用基本事实进行推理论证。又如，在课例2中，学生借助手持图形计算器，展示了截面图形在正方体表面投影形状的变化，较好地实现了抽象思维过程可视化。

探究活动中，信息技术的恰当使用，有效地拓展了探究方式，优化了学生观察、操作、发现、猜想、推理、论证、体验和实践等系列化探究的过程，提升了数学探究的效率、质量和育人功能。

三、借助信息技术探究截面性质，实现研究成果的可视化

教师采用项目式学习的方式教学，利用信息技术引导学生探究正方体的截面问题，有助于激活学生的理性思维，得到富有价值的探究成果。两个课例的成果汇报展示表明，学生不仅给出了具有广泛价值的结论，而且给出了具有推广深度的结论，超出预期，非常精妙，说明了信息技术对学生提升研究能力与创新意识有加持作用。

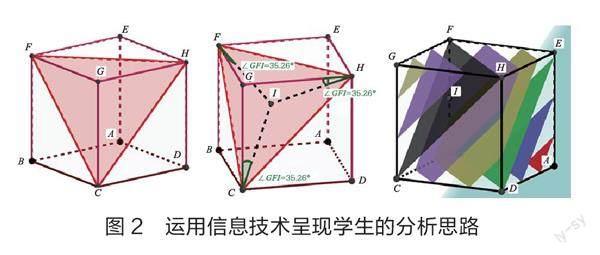
例如，在课例1的成果展示活动中，为完成第2个探究任务，学生使用GeoGebra动态跟踪轨迹功能，演示截面为三角形和四边形的各种情形，并经过探究，利用基本事实证明了“截面不可能是直角梯形”的结论。又如，在探究是否存在平面与正方体每条棱所在直线所成的角相等时，学生借助GeoGebra先找出棱GF、GH、GC与底面FGH所成的角相等，再利用GeoGebra动态跟踪轨迹功能，模拟平面与正方体相截的过程，观察与截面FCH平行的平面系（如图2），直观地感受和认知。

再如，在探究正方体所得截面面积何时最大时，教师引导学生按照从特殊到一般的思路，先直观比较正三角形、菱形、矩形、正六边形等几个特殊图形的截面面积的大小，再考虑一般意义的截面面积取得最大值的各种情形，最后让学生结合数学运算和逻辑推理得出截面为矩形时面积最大，即任意一个平面截正方体所得截面面积的最大值为棱长的倍。

教师将引导学生利用信息技术深度探究正方体截面作为一条主线，有利于学生在直观中学会抽象、在探究中学会提炼、在推理中学会表达。

四、借助信息技术推进探究过程，实现育人价值的智能化

两个课例中，教师均借助信息技术推进探究过程，围绕正方体截面的探究要求，让学生自主确定探究课题、设计探究思路、选择探究方法，让信息技术、动手操作和数学实验伴随探究活动的全过程，突出了学生的主体地位，改变了满堂讲、满堂问、满堂练的教学模式，充分发挥了信息技术辅助数学探究的价值功能。

教师利用信息技术，引导学生在项目式学习活动中探究，将探究问题聚焦在学生的兴趣点上，能有效激发學生的好奇心、想象力和探究欲，培育学生的探究意识、创新精神和实践能力。两个课例中，信息技术运用之巧、项目式学习方法之妙、探究活动成效之好，都达到了新的高度。各种信息技术和数学实验交融，让学生如身临其境全程参与，凸显了数学探究活动的跨学科育人价值，实现了教学的个性化、高效化和智能化。

总之，在数学探究活动教学中，教师合理地使用信息技术，可以有效地帮助学生建立数学直观，提升理性思维，让学生在问题情境中，感悟数学的本质，发展数学核心素养，养成数学探究学习的良好习惯。

参考文献

[1] 张永刚．“兴趣”引领，“项目”实施——“正方体截面的探究”教学设计与反思[J].中国数学教育，2021（3）：45-52．

[2] 李智伟．改变学习方式，凸显数学育人——“正方体截面的探究”教学设计与反思[J]．中国数学教育，2021（3）：45-52．

[3] 周李晓，李征．借助GeoGebra进行正方体截面问题的可视化探究[J].中小学数字化教学，2022（2）：57-60．

（作者周远方系湖北省教育科学研究院正高级教师、特级教师，苏步青数学教育奖获得者；张利系湖北省教育考试院助理研究员）

责任编辑：祝元志