追问，循序渐进开启思维

谢静

【摘要】追问是一门艺术，恰到好处的追问能有效开启学生的思维，开发学生的智慧.高质量的追问可有效拓宽知识的纵深与横宽，提高教学成效.基于此，文章以“数列中一类存在性问题”的复习教学为例，借助两道典型的数列例题，分别从追问于疑难处、错误处、独特处等展开教学设计与分析，并提出了追问应遵循从无到有的规律、追问应该关注适度性、追问需注重灵活性的教学思考，以期给高中一线教师提供一些参考.

【关键词】追问；思维；错误；数列

引 言

追问属于课堂提问的后续，是解决问题后的下一个教学步骤，它体现了教师的专业水平与教学机智.追问讲究一定的艺术性，在课堂教学中，教师切忌在追问环节滥问、乱问，要注意追问的每一个问题都要与前一个问题相关联，同时要注重追问的方式、方法与时机.

一、展示教学片段

（一）在疑难处追问

高中数学知识有较强的抽象性与逻辑性，学生常会似懂非懂，若教师在此处追问往往能成功引发学生的深度思考，让学生对知识产生更深刻的认识，克服因思维定式产生的一些问题.因此，教师在知识的疑难处追问具有克服思维程序化的作用，能让学生的思维变得更加清晰.

例1 已知{an}的通项公式an=2n，是否存在正整数p，q，r（p

教师选择一名学生的不完整解题过程进行投影：

解 如果存在这样的正整数，也就是2aq=ap+ar，那么2q+1=2p+2r.

师：接下来该解决什么问题了？

生1：应该是方程问题，但这里出现了3个未知数.

生2：将等式的两边同时除以2p，就能解决未知数的问题，具体过程为2q+1-p=1+2r-p，鉴于p1，r-p>0.等号的左边结论为偶数，而等号右边的结论是奇数，因此这种情况不存在.

追问1：为什么会想到将等号两边同时除以2p呢？

生3：因为这个方程的变量比较多，所以考虑到除以2p能减少变量.

追问2：但事实上这么处理后，变量的数量并没有减少，对吗？

生3：将q+1-p与r-p都视为整体，那么问题就從三元转化为二元了.

追问3：不错！这里呈现了什么数学思想？

生4：整体思想.

设计意图：面对学生的疑惑，教师给予学生充足的时间进行分析、讨论、探究，并以逐层深入的追问方式为学生的思维指引方向，此处的追问相当重要，它给学生带来了启发.

（二）在错误处追问

错误在数学教学中时有发生，如何利用好学生的错误，化错误为宝贵的教学素材呢？实践发现，在学生的错误处加以追问，往往能化“错误”为“领悟”，达到意想不到的教学成效.

接着以上教学片段，教师可继续追问：为什么将等式的两边同时除以2p，不除以其他呢？

生5：因为p是最小的，如此可确保指数部分均为正整数.

生6：我认为也可以除以2r.

师：哦？这是一个最大的量，是否可行呢？我们一起来看生6的解题过程（投影）：2q+1-r=2p-r+1，鉴于p

生6：两边都小于2，不会出现矛盾.

师：那咱们再回过头来看看，题中还有什么条件是没有利用到的？

生6：“p，q，r为正整数”这个条件未用到.

追问4：将这个条件考虑进来，指数部分的范围是否有什么变化？

生6：考虑到这个条件，有q-r≤-1，p-r≤-2，q-r+1≤0.

追问5：据此有什么新的发现吗？

追问6：不错！现在我们回过头来看看，之前未发生矛盾的根源是什么？

生6：是因为对“p，q，r”的条件未考虑全面，致使等式两边的范围都扩大了.

师：非常好！出现这种错误的根本原因就是等式两边函数的定义域太大致使值域也大了.

设计意图：学生的易错点是课堂教学值得关注的点，教师应紧扣这样的契机实施追问，并给予学生充足的时间与空间进行思考与分析，让学生对错误产生深刻的认识，避免类似情况再次发生.

（三）在独特处追问

1.尊重个体差异，追问在多解或归一处

受个体差异的影响，学生对同一个问题会产生不一样的理解.教师应尊重学生的个体差异性，从学生的“元认知”出发，追本溯源，关注大部分学生的想法，切忌只将目光锁定在“学优生”身上.

有时学生所展示出来的不起眼的思路，教师若能顺应他们的思维向下耐心引导，往往能起到事半功倍的效果.一题多解、多解一题都是优化解题方法，提炼“通性通法”的重要途径，而适时追问则是促进学生思维发散、优化、收敛的过程.

师：通过以上探究，我们发现选择最大与最小均能激发矛盾，那么选择中间的是否可以呢？

追问7：该生是通过范围激发矛盾，是否还有其他方法呢？

生7：根据左边为分数，右边为整数，同样能发现矛盾.

追问8：通过对以上几条路径的回顾，说说它们之间存在怎样的共性特征？

生8：同时除以一个变量的目的是一样的，均为消元，虽然矛盾形式不一样，但均与范围相关.

追问9：为什么都与范围相关？

生9：因为整分数与奇数、偶数都是观察两边范围发现的.

教师充分肯定了学生的说法，并与学生一起总结回顾以上教学流程与解题方法.经过师生、生生交流、归纳与总结，形成图1（板书）.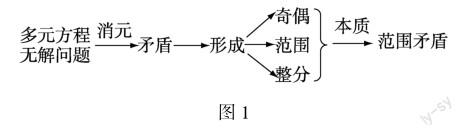

设计意图：在尊重学生个体差异性的基础上，通过适当的追问给学生提供了充足的思维空间，学生能在有的放矢的课堂中感受学习带来的愉悦感，进一步拓展了思维的宽度.

生1：觀察两边的取值范围，存在公共部分，代表问题有解，但不太好计算.

师：很好！本题与例题1有区别，这是研究“有解”的问题，是否存在其他的解题思路？

生2：根据函数的表达式可想到用m表示n.

追问2：如此表示有什么作用吗？

生2：仅需考虑等式一边的范围即可.

追问3：为什么不用n表示m？

生1：若用n表示m，则需要进行开方运算，且表达式异常复杂，不便于运算.

追问4：这名学生的解题过程有没有什么问题？

生2：这么解不对，其中关于m≥7时“是否成立”没有交代清楚.

生3：只要求出m≥7时分母的取值范围即可.

生4：还可先缩小m的取值范围，再取值.

追问5：怎样缩小m的取值范围呢？

生4：根据n>0，可知-2m2+4m+1>0，此时m的取值范围就小了.

追问6：你是怎么想到这种方法的？

生4：其实等式两边变量具有相互牵制性，因此我想到了用n的取值范围限制m的取值范围.

追问7：此处仅仅是n>0的限制吗？

生4：本应为n>m，本题仅需考虑n>0的情况.

互动至此，教师带领学生将以上探究进行一次小结，并板书：

追问8：这两种方法哪种更好一些？

生5：个人感觉第一种方法更简单一些，但第二种方法的功能更强大一些，若m为大数，列举就没那么容易了.

师：正是如此！我们将第二种方法作为解决这一类问题的通性通法.

设计意图：一个不完整的解题过程具有典型代表意义，教师通过循序渐进的追问帮助学生慢慢理清运算路径与解题思路，不仅让学生明确了运算的方向，还感知了“分离”的作用，掌握了解决这一类问题的通性通法.由浅入深地引导与追问，成功发散了学生的思维，提高了学生思维的灵活性.

二、教学思考

（一）遵循从无到有的规律

数列存在性问题一般以解决问题的形式出现在高考试卷中，这是复习教学的重点与难点.不少学生一看到这类问题就感到害怕，还未思考就打退堂鼓.本节课，教师以循序渐进的追问，带领学生抽丝剥茧，逐渐暴露问题的本质，为形成解决这类问题的通性通法奠定了基础.学生的思维也经历了从无到有的过程，整体来说收效颇丰.

课堂上，教师带领学生从一类不定方程的问题出发，切口小，难度适中，问题具有代表意义.教学设计体现“无解→有解”“无限→有限”，恰到好处的追问，帮助学生成功地克服了一个又一个障碍，学生思维真正意义上实现了“无→有→优→精”.

（二）追问需关注适度性

追问的时机相当重要，问得过早，达不到预期效果；问得过晚，学生的思维已经冷却.恰到好处的追问于思维的混沌处，能让学生产生豁然开朗之感；追问于思维的临界点，可催生学生新的认知；追问于思维的僵持点，可帮助学生突破瓶颈，柳暗花明；追问于思维定式时，可开阔学生的视野，跳出窠臼.追问绝非随意问、滥问，指向不明确或毫无意义地问，只会浪费宝贵的教学时间，难以达到预期效果.

（三）追问需注重灵活性

课堂具有动态变化的特征，不是所有教学环节都能靠预设完成.教师应有较高的专业素养，根据实际情况灵活调整教学策略，包括追问的时机、内容与方法等，这些都是实施教学的必备素养，体现了教学机智.如本节课，当学生的解题思路出现偏差时，教师没有直接揭示正确方法，而是耐心倾听学生的想法，通过循序渐进的追问，让学生自主发现错误根源，避免类似情况的再次发生.

结 语

总之，追问并非课堂教学的目标，通过追问这种方式引导学生更进一步掌握知识内容，获得学习能力才是追问的真正目的.教师应拥有良好的追问意识，要提出高质量、有品位的问题，以彰显教育的艺术与智慧.

【参考文献】

[1]龙艳文.基于概念生成中三个层面追问的问题串设计[J]数学通报，2017（03）：11-13，17.

[2]郭建理.基于深度学习的高中数学课堂教学问题设计[J].中小学课堂教学研究，2021（12）：57-60.

[3]李潇潇.高中数学教学“问题链”设计研究[J].武汉：华中师范大学，2021.