近海V形山谷地形输电线路的风场仿真与风灾事故分析

章李刚 何鑫 徐海巍，* 余世策

（1.浙江华云电力工程设计咨询有限公司， 杭州 310014； 2.浙江大学结构工程研究所， 杭州 310058）

0 引 言

我国海岸线漫长，沿海地区山地覆盖率较高（如浙东地区）。为了满足沿海地区经济快速发展的需要以及解决电力资源东西部分布不平衡的问题，近年来沿海地区的电网建设规模迅速扩大。大量的输电走廊难免会经历山区地形，而复杂地形地貌所产生的微气象则对输电线路的安全和可靠提出了巨大挑战。输电线路跨度大且体型轻柔，属于风敏感结构，风荷载是其设计的主要控制因素。而复杂的地形变化将影响来流的风场特征，从而形成加速、衰减效应以及复杂三维绕流特性。风场的这些特性变化将增加输电线路结构的灾害隐患。随着恶劣风气候的日益增加给电网带来了巨大损失。如2019年台风利奇马影响下浙江沿海某城市线路出现了超过200多次的跳闸［1］，造成了重大经济损失。大量的电网风灾事故表明，复杂地形下线路的倒塔以及跳线的风偏闪落等事故发生概率更高，这是由于大风天气加乘复杂地形微气象的不利影响所致。因此，复杂地形下风场特性的研究也引起了国内外专家学者的广泛兴趣。

目前对于山地地形风场特性的研究方法主要有现场实测、风洞试验和计算流体力学（CFD）数值模拟等。以往研究多数集中在典型的单山或者双山地貌，沈国辉等［2］针对理想化的单山和双山风场了风洞试验研究，得到了相应的风场特征。徐海巍等［3］考虑了余弦型单山脉地形对风场的影响，通过风洞试验进行了输电线路跳线的风偏分析，并指出微地形下跳线发生风偏的风险明显高于平坦地貌。王璋奇等［4］针对垭口型微地形的风场特征进行研究并拟合了垭口地形风场修正系数。楼文娟等［5-6］研究了典型的山地风场特性及其对输电线路风偏响应的影响。Ishihara等［7］采用风洞试验模拟研究三维山丘在山体不同位置处的风速分布，发现在山顶和山腰等位置处风速有明显增大。Okamura等［8］则通过风洞试验流场显示技术对二维山体周围风场进行了研究，发现山体背风侧的气流存在向下的分量。李正良［9］等对于一系列变高度和坡度的单山地貌进行了风速的加速效应研究，并拟合了坡度为0.13～0.5之间的山丘地形的风速修正经验公式。

然而，实际输电工程建设场地是包含多种特征地形相综合的复杂山区地貌，上述基于经典山地模型得到的风场结论可能存在适用性困境。因此，对于真实地形环境下的风场特征开展研究更具有现实指导意义。而随着地理高程信息模型的不断完善以及三维倾斜摄影等技术的迅速发展，使得三维高精度地形建模成为了可能。近年来关于复杂真实地形的风场研究也取得了不少进展。Momomura等［10］对某真型山区输电线路进行现场实测并通过风洞试验对山地风场进行了模拟。国内不同学者［11-12］也分别对山区桥梁选址处的深峡谷地形风场开展现场实测研究。祝志文等［13］和李永乐等［14］分别基于CFD仿真模拟了复杂山区桥址附近深峡谷地貌的风场并分析了地形对风场的影响。张希斌［15］基于插值多尺度剖面法（IMP）对香港某复杂山地进行了风场仿真。李达等［16］对广东某岛的真实复杂山地进行建模和数值仿真，并将仿真结果与流迹显示（PIV）试验结果进行了对比。

在我国沿海地区，一类较为典型的地形是两座延绵相交的山脉间存在较为平坦的山谷，且往往为村镇所在地。为了供电需要，线路有时要穿越山谷而建。因此，对于该类地形下的风场特征有必要开展深入探索，而以往研究对于此类地形关注较少，从而给线路抗风设计带来了不确定性。本文以跳线风偏闪络事故多发的典型浙东沿海某V形山谷地形为例，分别开展了基于雷诺时均模拟（RANS）和大涡模拟（LES）的CFD风场仿真研究，考察了不同地形尺度对风场模拟精度的影响，在此基础上分析了输电线路风灾事故发生的可能原因。相关研究结论可为类似地形输电工程开展抗风设计提供参考。

1 事故点地形建模

1.1 事故地点概况

本文研究地形位于浙江东南沿海地区，属于近海山区。其地形特征和线路如图1所示。该事故点地形包含两侧分别高约为350 m（西侧山脉）和260 m（东侧山脉）的交错山脉，以及交错山脉之间形成的V型开阔山谷。山谷的开口处面向大海。一条高压输电线路穿越两座山脉，其塔号为图中的19～23号，其中跳线仅位于21号转角塔。此外，为分析该地形下特征位置的风场情况，分别增设山顶和山谷的典型位置点Z1和Z2以作考察。

图1 事故点地形及线路塔位Fig.1 Terrain of accident point and line tower position

2020年第四号台风“黑格比”在浙江温州登陆，其中心最大风力13级。登陆期间造成该线路21号塔引流线及塔身上有明显放电痕迹（图2），引起线路4次跳闸。灾后初步调查分析认为，可能是由于台风作用下风速超过设计值所致，但其具体原因和地形的不利影响仍有待探明。

图2 塔身放电痕迹Fig.2 Discharge trace of tower body

1.2 地形的建模与前处理

根据经纬度确定事故线路所在的地形区域，如图3所示。为了考察不同仿真区域对事故线路风场的模拟效果以提出合理的仿真范围，以事故塔为中心，分别提取半径为3 km、5 km、8 km的地形模型用于后续数值仿真的对比研究。三种地形尺度范围见图3。

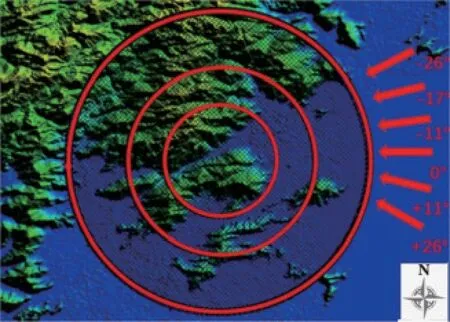
图3 地形选择范围及来流风向示意图Fig.3 Topographic selection range and incoming wind direction

由于地形切割会在边缘处形成人为的峭壁，如图4所示。这种垂直切面会对来流风场产生较大的影响。为了避免此处风速的突变，对切割地形边界进行流线化平滑处理。通过引入过渡函数式（1）处理后［15］，边界处呈缓变态势，如图5所示，可以满足数值仿真要求。

图4 未处理地形Fig.4 Unprocessed terrain

图5 处理后地形Fig.5 Terrain after treatment

式中：R2为切割地形总半径；R1为切割地形内保留部分半径；R1与R2之间的部分即为需要处理的过渡段。R1、R2取值视边界陡峭程度和处理后效果而定，本次模拟中过渡段距离取为500 m。

2 真实地形的CFD仿真

2.1 计算域与网格

采用计算流体动力力学软件ANSYS FLUENT对图5所示地形模型进行数值模拟。模型缩尺比选为1∶1 000，计算域设置和坐标系选取如图6所示。其中R为仿真地形半径，H为仿真地形最大高度。模型阻塞率约为3%，小于《建筑工程风洞试验方法标准》（JGJ/T 338—2014）中规定的阻塞比要求。首先，采用RANS湍流模型对不同尺度的地形进行模拟，以考察仿真地形选取的合理性。随后，选用RANS湍流模型和LES大涡模型对相同地形进行模拟，以比较不同模型对仿真结果的影响。最终，选取合理的仿真模型和地形模型进行该V形近海地形风场的仿真研究。为了保证计算精度，对整个流域进行结构化网格划分，并对地形近壁面网格进行加密。

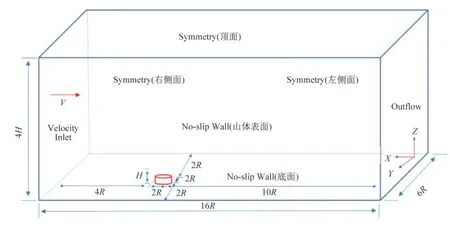
图6 计算域与边界条件Fig.6 Calculation domain and boundary conditions

RANS模型中，近壁面第一层网格高度取为0.005 m，网格增长率取为1.2。模拟的三种尺度地形（3 km、5 km、8 km）对应网格数量分别为235万、536万、1 700万。模拟中速度和压力的耦合采用Simple算法处理，对流项离散格式均采用二阶迎风格式。采用粗糙度高度指标ks来表征地表粗糙度。根据已有文献［17］，本文中地面ks取为0.5，山体上取为1.0。计算域入口定义为速度入口，出口为自由流出，左侧、右侧和顶部采用对称边界，计算域底部及山体表面为固定壁面，如图6所示。

LES模拟中，保持与RANS方法同样的计算域尺寸和缩尺比，第一层网格高度设为0.001 m，增长率为1.2，网格总数为1 880万，计算时间步长为0.000 1 s，迭代步数为6 000步。入口处采用窄带随机湍流合成（NSRFG）方法生成湍流风场扰动［18］，数值求解格式如表1所示，数值模拟的收敛标准设置为10-4。

表1 大涡模拟求解格式Table 1 Large eddy simulation solution scheme

2.2 来流边界条件与计算工况

考虑台风事故发生时主导风向主要来自于山谷临海一侧，故在计算仿真中主要考虑来自海面方向的风场作用。入口的风剖面选为A类地貌风场。对于RANS采用Realizablek-ε模型（简称RKE），入口处采用用户自定义函数（UDF）进行设置，时均速度入口采用指数分布的风速剖面（式2），

式中：Z0、V0分别为参考高度（本文取10 m）和参考处风速（本文取10 m/s）；Z、V分别为流域中任意点的高度和该高度处的平均风速；α为来流地面粗糙度指数，取为0.12。

湍流度I（z）和湍流积分尺度Lu参考日本规范取值，见下式：

式中：Zg为梯度风高度取300；Zb按照日本规范取5 m。

此外，湍动能k(z)和湍流耗散率ε(z)的取值参照《建筑风环境测试与评价标准》［19］，如下式所示：

式中：ls为模型缩尺比；Cμ为湍流模型经验常数；α为地貌指数参数，一般取值为0.04；D1和D2分别为修正系数，对A类地貌分别取-1.391和4.617。

为检验上述流场的自保持性，对无山体空流域进行了分析，结果如图7所示。由图可见，该风剖面具有良好自保持性，可以满足计算要求。

图7 风剖面自保持检验Fig.7 Verification of self-sustaining of wind profile.

对于LES模型，其湍流度、湍流耗散率均根据文献［18］设置，边界条件与k-ε模型保持一致，以便后续对比。NSRFG方法通过时域叠加的方法重构满足要求的单点脉动风速时程，再扩展到三维空间中，从而构造出满足零散度条件、风速空间相关性和风速脉动功率谱等特征的脉动风速场。根据该方法获得的顺风向脉动风速表示为

式中：X为模拟位置坐标向量；Su（fn）为顺风向脉动风速功率谱，本文采用Von Karman谱进行模拟；xj中，j=1，2，3分别表示x、y、z方向；fn为频率，fn=(n-1/2)Δf，其中Δf为谱带宽；ϕn～U（0，2π）为均匀分布的随机数；kj，n为服从空间单位球面上均匀分布的随机数；cj为衰减系数；γj为调谐因子［18］。

仿真中主要对正对山谷附近风向的海面来流工况进行了分析。以正东方向来流为0°风向角，顺时针为正逆时针为负定义风向角。分别计算了-26°、-17°、-11°、0°、11°和26°这6个工况。风向角示意见图3。

2.3 网格与时间步长的无关性验证

为了节省计算资源同时保证仿真结果的合理性，通过设置具有不同密度的多组网格来进行网格独立性检验。这里选取半径范围为5 km的地形模型进行网格无关性验证，首层网格分别采用0.003 m（方案1）、0.005 m（方案2）、0.007 m（方案3）和0.009 m（方案4），增长率保持一致。

图8给出了某工况下21号塔位处三种网格划分方案的风速剖面模拟结果。总的来看网格方案1与方案2的风速剖面仿真结果较为接近，其他方案的模拟结果在存在一定的误差。综合计算精度与效率，最终CFD模拟中采用方案2的网格形式。

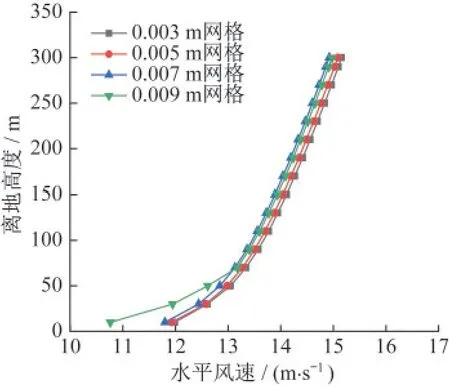
图8 不同网格方案在21号塔处风速剖面Fig.8 Wind speed profiles of different grid schemes at tower 21

为了考察不同时间步长对LES模拟结果的影响，对中尺度5 km半径地形进行三种时间步长工况计算，分别为0.000 5 s、0.000 1 s、0.000 05 s，每次计算迭代6 000步。图9给出了某工况下21号塔位水平风速比Su（山体表面离地高度与来流相同离地高度处的水平风速之比）剖面在不同时间步长情况下的模拟结果。其中0.000 5 s大时间步工况下计算收敛性较差，不能满足精度要求，而后两种时间步方案下的风速比剖面模拟结果较为一致。综合计算精度与效率，最终CFD模拟中采用0.000 1 s时间步长。

图9 不同时间步长21号塔处加速比Fig.9 Comparison of horizontal acceleration ratio of different time step at tower 21

2.4 不同地形尺度的计算结果比较

为了考察不同仿真地形尺度对风场模拟结果的影响，选取21号输电塔位置，采用RANS方法进行不同尺度地形模型下加速比风剖面计算结果的对比。

选取典型的-11°与-17°风向结果作对比分析，图10、图11给出了两个风向下的21号塔位的水平加速比。由图可知，5 km和8 km半径地形的下计算得到的水平加速比剖面较为一致，而小尺度3 km半径地形由于忽略了来流向的地形遮挡与干扰从而导致计算得到的风速结果整体偏大。图12、图13给出了这两个风向下的21号塔位的竖向风速比Sw（山地离地高度的竖向风速与相同离地高度来流水平风速的比值）剖面。从竖向风速比结果来看，中尺度（5 km）地形与大尺度（8 km）地形的结果仍更接近，而小尺度地形计算误差较大。综合考虑计算效率和精度，本研究选取5 km中尺度地形作风场分析较合理。

图10 不同尺寸地形-11°风向下塔21水平加速比Fig.10 Horizontal acceleration ratio under wind azimuth of-11° for tower 21 under different size terrains

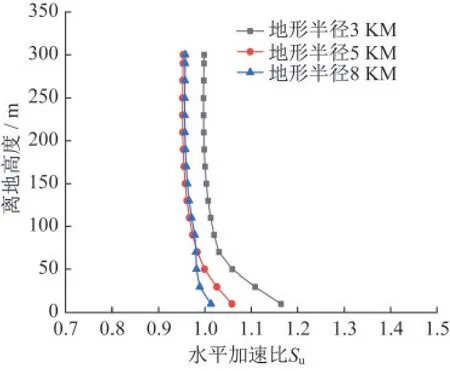
图11 不同尺寸地形-17°风向下塔21水平加速比Fig.11 Horizontal acceleration ratio under wind azimuth of-17 ° for tower 21 under different size terrains

图12 不同尺寸地形-11°风向下塔21竖向风速比Fig.12 Vertical wind speed ratio under wind azimuth of-11 ° for tower 21 under different size terrains

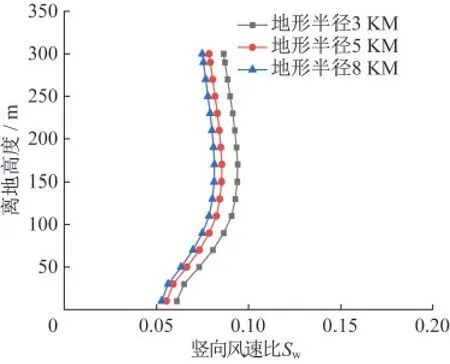
图13 不同尺寸地形-17°风向下塔21竖向风速比Fig.13 Vertical wind speed ratio under wind azimuth of-17 ° for tower 21 under different size terrains

2.5 RANS与LES模拟结果比较

为了考察不同仿真方法结果的差异性，分别采用RANS与LES方法对5 km尺度地形下的21号塔位在同一工况下进行模拟。图14和15分别给出了LES和RANS两种方法下，21号塔位处的水平和竖向平均风速比的仿真结果。由图可知，水平风速比的LES计算结果总体比RANS结果略大，且随着高度增加两者趋于一致，底部10 m高度处最大风速比模拟结果分别为1.18（RANS）和1.25（LES）。而关于竖向风速比，两种仿真方法得到的结果也略有差距，LES计算得到的最大竖向风速比可达18%，而RANS的对应结果约为15%。这是由于大涡模拟可以更好地捕捉不同尺度的涡，从而更加精确地反映风速的脉动贡献。

图14 塔21水平加速比的LES与RANS结果比较Fig.14 Comparison of Horizontal acceleration ratio at tower 21 between LES and RANS results

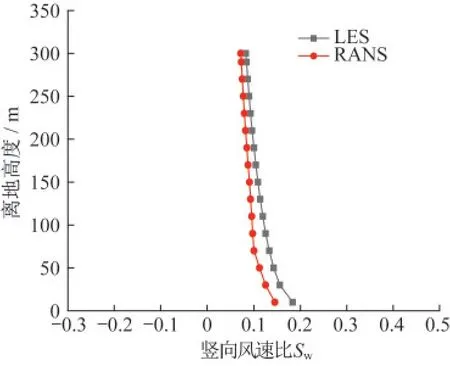
图15 塔21竖向风速比的LES与RANS结果比较Fig.15 Comparison of vertical wind speed ratio at tower 21 between LES and RANS results

3 结果与分析

考虑到LES模拟更具合理性，以下研究中主要采用该模型对5 km中尺度地形在不同风向角下的线路风场特性展开分析。

3.1 V型山谷地形的线路风场特征

选取19～23号塔位以及山谷中间Z1点和较高西侧山脊线迎风端Z2点作为特征位置进行风场分析。通过水平加速比Su来反映地形对水平风速的干扰效应。图16给出了某工况下150 m高度（近事故塔位）位置顺风向风速场的模拟效果。由图可见，复杂山地对于来流风速影响十分显著。

图16 顺风向水平风速云图（Z=150 m）Fig.16 Contour plot of along-wind horizontal speed field （Z=150 m）

图17—图21给出了5个塔位处水平风速的加速比剖面。由图17—图19可见，位于东侧较低山脉的20、21号塔在正风向角下（如0°～26°）无明显加速效应。而在正对东侧山脉的负风向（如-11°～-26°）上，三个塔位处水平风速出现显著加速效应，如10 m高度处3个塔在-26°风向下的水平加速比位于1.21～1.35。其中位于东侧山脊顶部的20号塔的水平加速比最大，其最大值约为1.35，而位于山腰位置的事故塔21号的最大水平加速比达到1.25。由此可见，地形对于风速的放大效应明显，进一步提升了恶劣风气候下（如台风）的线路风险。

图17 不同风向19号塔水平加速比Fig.17 Horizontal acceleration ratio of tower 19 in different wind directions

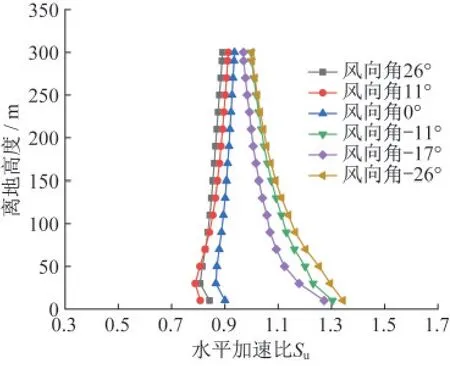
图18 不同风向20号塔水平加速比Fig.18 Horizontal acceleration ratio of tower 20 in different wind directions

图19 不同风向21号塔水平加速比Fig.19 Horizontal acceleration ratio of tower 21 in different wind directions

对于西侧较高山脉处的22号和23号塔，由图20、图21可见，22号塔在正风向角度下不存在加速效应，反而在负风向角度加速比略有提升。这是因为，22号塔处于半山腰位置，在0°～26°正风向下，22号塔处于西侧山脉的背风侧，遮挡效应明显（图22）。而对于山脊处的23号塔位，其在26°风向下取得最大加速比约为1.53（10 m高度），且随着来流风向角改变，最大加速比变化显著。

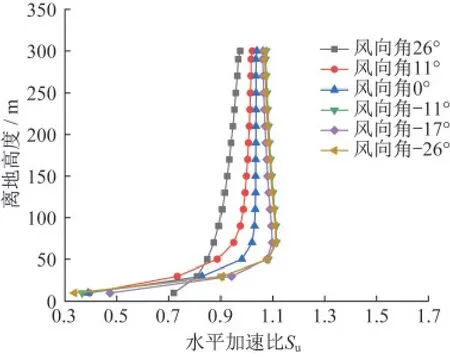
图20 不同风向22号塔水平加速比Fig.20 Horizontal acceleration ratio of tower 22 in different wind directions

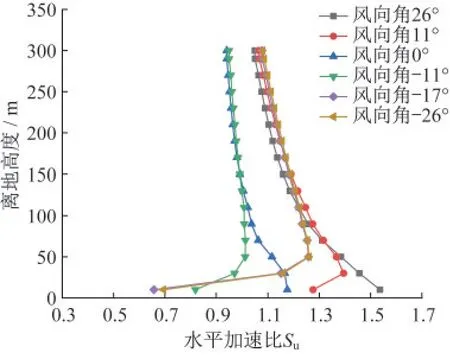
图21 不同风向23号塔水平加速比Fig.21 Horizontal acceleration ratio of tower 23 in different wind directions

图22 22和23号塔位处地形情况Fig.22 Topographic conditions at tower 22 and 23

图23、图24分别给出了山谷中心位置Z1处和西侧山脊迎风端最高点Z2的风速加速比剖面。由图可见，山谷中心Z1点位置处，不同风向下风速均无明显加速现象，反而由于受到山体遮挡而存在衰减（如26°风向）。而西侧山脊最高点Z2位置处风速的最大加速比在迎风时（26°）取得，可达到1.68，不同风向下加速比曲线较为接近。由于受到前部遮挡（图22），同样位于山脊线的23号塔相比最高位置点Z2的最大加速比有明显降低。

图23 不同风向山谷Z1位置水平加速比Fig.23 Horizontal acceleration ratio of Z1 position in valley with different wind directions

图24 不同风向山顶Z2位置水平加速比Fig.24 Horizontal acceleration ratio of Z2 position on the top of mountain in different wind directions

为了考察地形对竖向风速的影响，采用竖向风速比Sw来进行描述。图25～28给出了不同风向下20～22号塔位以及Z2位置处竖向风速比沿高度的变化情况。

图25 不同风向20号塔竖向风速比Fig.25 Vertical wind speed ratio of tower 20 in different wind directions

由图25和图26可知，东侧山脉上的20和21号塔的最大竖向风速比出现在26°风向下的10 m高度处，分别可达来流水平风速的49%和42%。随着高度增加，虽然竖向风速比呈现减小趋势，但水平风速却迅速增加，即使在50 m高度附近，20和21号塔的最大竖向风速比仍可达0.37和0.30左右。由此可见，地形影响下的上升气流不可忽略。已有研究［3］表明，对于轻柔的跳线结构，上升气流的存在将降低其张力和抗风能力，增加其发生风偏闪络的风险。

图26 不同风向21号塔竖向风速比Fig.26 Vertical wind speed ratio of tower 21 in different wind directions

图27和28显示，西侧山脉山腰位置的22号塔在26°和11°等正风向角度下出现了明显的负风速比，这是因为受到遮挡后气流翻过山脊在背面形成下沉趋势，此时竖向风由上升转变为下降形态。而在-11°～-26°风向下，22号塔的竖向风速比接近0，可以忽略。对于山顶Z2位置，其最大竖向风速比在-17°风向，约为0.38。

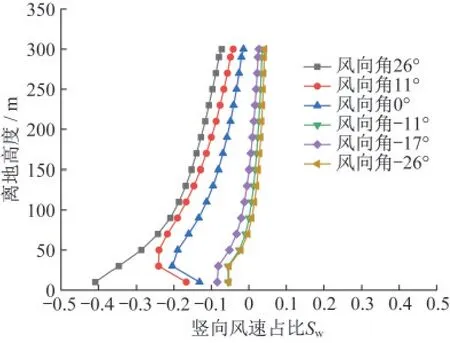
图27 不同风向22号塔竖向风速比Fig.27 Vertical wind speed ratio of tower 22 in different wind directions

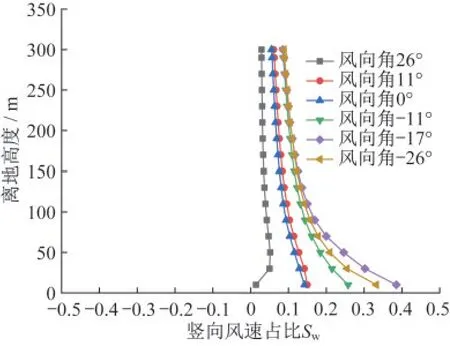
图28 不同风向山顶Z2点竖向风速比Fig.28 Vertical wind speed ratio of point Z2 on the mountain top with different wind directions

综合上述分析可知，东侧山脉顶的20号塔位和西侧山顶Z2位置分别在-26°和-17°风向下同时出现较大的水平风加速和显著的竖向风。因此，对这些不利位置处的线路抗风设计需要引起关注。而对于事故发生的21号塔位，其在不利的-11°风向下，跳线悬挂高度处（约30 m高度附近）的最大水平风速加速比可达1.2，而此高度的竖向上升风速仍可达来流水平风速的约15%，两者综合作用下可能引发跳线的风偏事故。

3.2 极值风速的放大效应

考虑到轻柔跳线结构对阵风的敏感性，有必要分析复杂地形对考虑脉动后的风速极值影响。针对离地10 m高度，采用规范方法［20］分别计算入口处和事故21号塔位处的极值风速，如下式所示：

极值风速与来流对应高度的平均风速之比，结果列于表2。由表2可知，相比来流极值风速，由于地形的影响导致事故塔位处极值风速又存在进一步的增加，即相比入口处极值风速放大约1.13倍。与此同时，竖向脉动极值风速也占到来流水平风速的约20%，这将影响跳线的抗风偏性能。考虑到强风天气（如台风）条件下，来流的风速均值和脉动相比常态风均有大幅提升，因此当考虑到地形的加乘效应后会加重线路的风灾风险，这也是历史风偏事故发生的重要原因之一。

表2 不同位置极值风速与来流平均风速比Table 2 Ratio of extreme wind speed to average wind speed of incoming flow at different locations

4 结 论

对某近海V形山谷地形分别采用了雷诺时均和大涡模拟仿真方法展开风场特性研究，探索了线路风灾事故发生的可能原因。主要结论如下：

（1） 中尺度5 km半径地形与大尺度地形结果较为接近，而3 km小尺度地形的仿真结果存在较大误差。大涡模拟方法的仿真结果比雷诺时均结果略偏大。

（2） V形山谷东西两侧山脉顶部的20号塔位和Z2位置受到的水平风加速比和竖向风均较为不利。其中，水平风速比最大值分别可达1.35和1.68，最大竖向风加速比分别可达0.49和0.38。因此，在线路抗风设计中应引起重视，尽量避开上述不利受风位置。半山腰22号塔位处的水平风加速效应不明显，但在背风向时存在下沉风速。

（3） V形山谷的中心位置处未发现明显的风加速效应，反而在某些风向下出现衰减。

（4） 事故塔位在特定风向下同时存在较大水平风加速比和竖向风速比。当考虑阵风效应时，地形的影响将使得来流风速极值增大13%，同时产生明显的竖向极值风，从而在强风作用下提升了跳线发生风灾事故的风险。