海上风机规范风浪荷载计算方法对比分析

李公豪 袁周驰，* 梁发云

（1.同济大学岩土及地下工程教育部重点实验室，上海 200092； 2.同济大学土木工程学院，上海 200092）

0 引 言

近年来，随着人类对可再生能源的需求日益增长，使得当今世界的风能产量飞速提升。相比于陆上风电，海上风电具有更高质量的风能资源、更少的空间限制以及无需考虑噪声污染问题等优势［1］。然而，海洋区域存在着强风和波浪等极端环境条件，海上风机所承受的水平荷载和倾覆力矩要比陆上风机大的多，可能导致风机在极端条件下产生过大的倾斜甚至结构破坏。因此，合理计算作用在风机结构上的风浪荷载对于海上风机设计非常重要。

在海上风机设计中，风荷载和波浪荷载是主要的外部荷载，不同规范在风荷载和波浪荷载的计算上存在着参数及公式选取等方面的差异。因此一些学者针对风荷载和波浪荷载的计算开展了规范对比，其中吴海涛［2］对比分析了不同规范中的海上风电小尺度结构物波浪载荷；宋波等［3］研究了国内外典型规范的风电塔架在风荷载、地震荷载和波浪荷载作用下的设计要求；湛杰［4］针对近海风浪荷载的中美日规范进行比较并探讨了其取值方法的差异；马林静等［5］对比分析了不同规范中的风电机组荷载。上述文献［2-5］的海上风机风浪荷载计算主要依据于这几本规范：中国船级社（CCS）《海上风力发电机组认证规范》［6］（2012年版本）、国际电工委员会（IEC）的《海上风力发电机组设计标准》［7-9］（2005年版本）、挪威船级社（DNV）的DNV-OS-J101规范［10］（2014年版本）和德国劳氏船级社（GL）的GL规范［11］（2010年版本）。在技术进步和现实需求之下，海上风机规范的版本不断更新。例如德国劳氏船级社和挪威船级社合并后，推出了新版本的DNV GL系列海上风机规范；CCS在2021年发布的《海上风力发电机组认证指南》［12］（下文简称CCS规范）、IEC于2019年推出的《风力发电机组设计标准》［13］和《固定式海上风力发电机组设计标准》［14］（下文简称IEC规范）、DNV GL于2016年推出的《风力发电机的环境条件与荷载》（DNV GL-ST-0437）［15］（下文简称DNV GL规范）。

CCS规范、IEC规范和DNV GL规范均对风荷载和波浪荷载作出了具体的规定，它们对于风浪荷载的计算原则大致相同，但在参数选取和计算公式上有所不同，使得计算得到的风浪荷载也会有所差别。在风荷载计算中，上述三本规范的计算思路大致相同；在新版规范中，风荷载计算方面的变化主要是CCS规范、IEC规范和DNV GL规范均扩展了风机等级，而DNV GL规范对风况模型计算公式进行了更新。在波浪荷载计算中，IEC规范采取了国际标准ISO 19902—2020（石油和天然气工业-固定式海上结构物）［16］，DNV GL规范详细描述了波浪荷载的计算要求，总体与ISO19902-2020的思路一致，CCS规范在波浪荷载计算方法上与前两者也基本一致，但在波浪荷载计算的水动力参数选取上存在一些差异。

本文主要从上述最新版本规范的差异出发，选取CCS规范［12］、IEC规范［13-14］和DNV GL规范［15］对比三者在风浪荷载计算上的差异，并以某海上风机工程为例，对比不同规范的计算结果，给出了规范选取和参数确定的建议，为设计和研究人员提供参考。

1 风荷载计算方法的对比分析

海上风机的荷载计算与基础设计较为复杂，两者是相互依赖的，基础设计需要荷载计算提供输入到基础上的荷载，而荷载计算则需要基础模型才能进行，两者互为输入条件，一般情况下需要根据现场条件预估荷载，完成基础的初步设计［17］。CCS规范与IEC规范在风荷载计算上基本相同，本节以选取的CCS规范和DNV GL规范比较它们在风荷载计算的差异，其差异主要体现在风电机组等级和风况模型。

1.1 风电机组等级的差异

对于风力发电机组的设计，规范要求了两类安全等级，包括一般安全等级和特殊安全等级（S）。一般安全等级是指若结构失效，会导致人身安全或造成经济损失和产生社会影响。采用特殊安全等级时，设计值由设计者给定，在设计文件详细说明。安全等级不同，海上风机所能承受的环境条件也不同，风荷载的计算所采用的风况参数也就不同。风荷载的计算涉及风机等级和对应等级的湍流强度参数。

最新的CCS规范与DNV GL规范在风机等级的差异包括等级划分方法与湍流强度参考值。

风机等级的划分依据两类参数，一是风速参数，包括年平均风速和参考风速，风机被划为Ⅰ、Ⅱ、Ⅲ及S级，如表1所示，两规范在这一部分的等级划分方法是一致的；二是环境参数或湍流参数，如表2和3所示，DNV GL规范所考虑的环境参数包括了50年一遇参考有义波高及对应的波周期、湍流强度参考值、湍流偏移因子和形状因子，而CCS规范只考虑湍流参数，即湍流强度参考值。

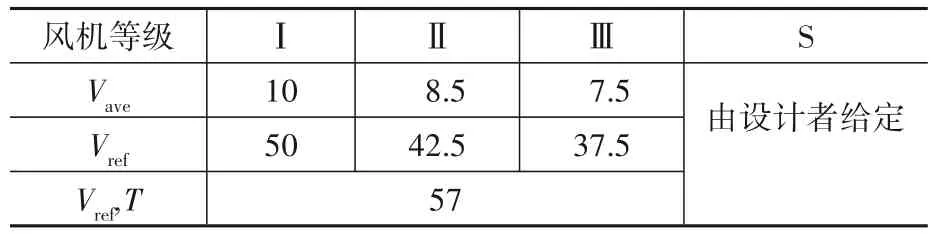
表1 各等级海上风机的风速参数（CCS、DNV GL）Table 1 Wind speed parameters of different grade offshore wind turbine （CCS、DNV GL）

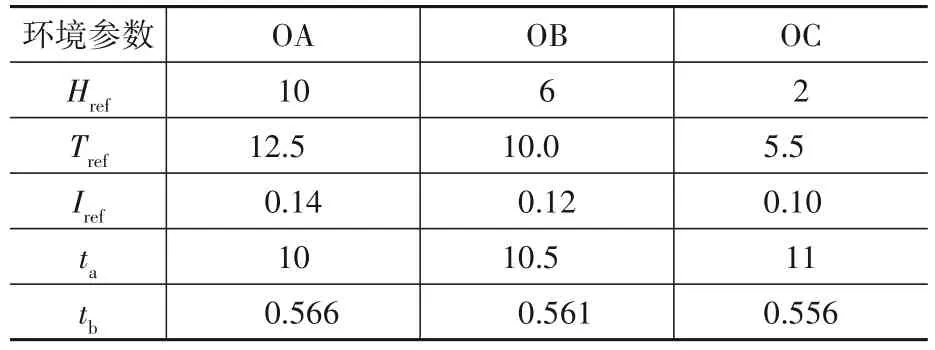
表2 各等级海上风机的环境参数（DNV GL）Table 2 Environmental parameters of offshore wind turbines of different grades （DNV GL）

总体上，相比旧规范，最新的CCS规范为了让风机在具有较高极限风速的地区也能应用，增加了台风型的参考风速，但实际上与陆上风机等级划分方法是一致的［18］。而DNV GL规范的等级划分对海上和陆上进行了区分，其海上风机等级在陆上风机等级基础上增加了对波浪参数的考虑，对湍流的考虑也更细致。

在湍流强度参考取值上，如表3和表4所示，CCS规范划分了4个等级，从高到低包括A+、A、B和C，对应的取值为0.18、0.16、0.14和0.12。而DNV GL规范划分了3个等级，分别为OA、OB和OC，对应的取值为0.14、0.12和0.10。相比陆上风电，海上风电风能资源的湍流偏小［1］，所以DNV GL针对了海上风机等级划分了较低湍流强度参考值。

表3 各等级海上风机的湍流强度参考值（CCS）Table 3 Reference values of turbulence intensity of offshore wind turbines of different grades （CCS）

表4 各等级海上风机的湍流强度参考值（DNV GL）Table 4 Reference values of turbulence intensity of offshore wind turbines of different grades （DNV GL）

表1—表4中数据为轮毂高度处的数值，Vave为年平均风速，Vref为10 min参考平均风速，Vref，T为台风型风机的10 min参考平均风速，上述风速参数单位均为m/s，Iref为湍流强度参考值，在平均风速为15 m/s时湍流强度的期望值。Href为50年一遇参考有义波高，单位为m；Tref为Href对应的波周期，单位为s；ta为湍流偏移因子，单位为m/s；tb为湍流形状因子。

1.2 风况模型的差异

风况作为外部环境条件之一，是风荷载计算重要的影响因素，描述风况模型的关键参数之一是湍流强度。

CCS规范与DNV GL规范在风况模型描述的差异主要是正常湍流模型和极端湍流模型的湍流标准差计算公式不同。下面以表格的形式将CCS规范与DNV GL规范在风况模型的差异进行展示，见表5。

表5 不同规范湍流模型差异Table 5 Difference of turbulence model in specification

湍流模型中的计算离不开湍流强度参考值，所以CCS与DNV GL在风机等级划分中湍流强度的差异也将影响到这里的计算。在极端湍流模型中，两规范所考虑的参数一致，计算公式略有区别。在正常湍流模型中，DNV GL的计算公式考虑的影响因素比CCS要多一些，包括湍流偏移因子、湍流形状因子及表面粗糙度等。

1.3 风荷载计算方法

CCS规范与DNV GL规范均没有对风荷载的计算方法做出细致要求，仅对风场及风机荷载的模拟进行了要求。在实际情况中，风荷载是作为风电机组荷载的一部分由风机厂商按照规范要求模拟之后提供给基础设计方［19］。风荷载计算方法除了风机厂商常用的有限元模拟方法，还有下部结构与基础设计常用的等效静力法和推力系数法［20］。

等效静力法是在基本风压之上考虑峰值因子等参数，得到风荷载峰值［20］。推力系数法来源于Betz理论关于风机风能效率的推导。相比等效静力法，推力系数法源于风与风机的气动理论。但其建立在理论风机上，与实际风机在叶片数量和流体特性是有所差别。Frandsen［21］给出了推力系数在实际风机应用中的取值建议，Arany等［22］从基础设计的角度推荐了推力系数法并给出了推力系数的计算公式，即式（1）。

所以在海上风电基础问题及相关研究中，常采用推力系数法来计算风机的风荷载。因此，本文采取推力系数法来计算风荷载。

式中：Fwind为风荷载；ρa为空气密度；AR叶片扫掠面积；CT为推力系数；V为风速；Vin为切入风速，风机启动的最低风速；Vout为切出风速，风机停机的风速。

风速分成两部分，平均风速和湍流风速：

各风况湍流风速计算见表6，其计算公式参考Arany 的总结［22］。将不同风况下的湍流风速代入到式（3）中v，再将式（3）代入式（1）即可计算风荷载。

表6 各风况湍流风速计算公式Table 6 Calculation formula of turbulent wind speed

2 波浪荷载计算方法的对比分析

波浪荷载计算主要涉及到海况模型的要求、波浪参数的计算及波浪荷载计算公式三个方面。对于海况，CCS规范、IEC规范和DNV GL规范均划分为正常海况、恶劣海况和极端海况。正常海况是考虑长期联合概率分布给出波浪参数。恶劣海况考虑的是随机的恶劣海况模型与正常风况的组合。极端海况需要考虑重现期为1年和50年的波浪参数。CCS规范、IEC规范和DNV GL规范在海况的规定上没有差异。DNV GL规范与IEC规范在波浪荷载计算上基本相同，故本节以选取的CCS规范和DNV GL规范为例比较它们在波浪荷载计算的差异，其差异主要体现在波浪参数和水动力系数的确定。

2.1 波浪参数

波浪参数的计算包括波高和对应波周期的计算。主要涉及根据50年一遇有义波高计算1年的等效值及确定对应的波周期范围。CCS规范与DNV GL规范在计算极大波高上存在细微差异，见表7。

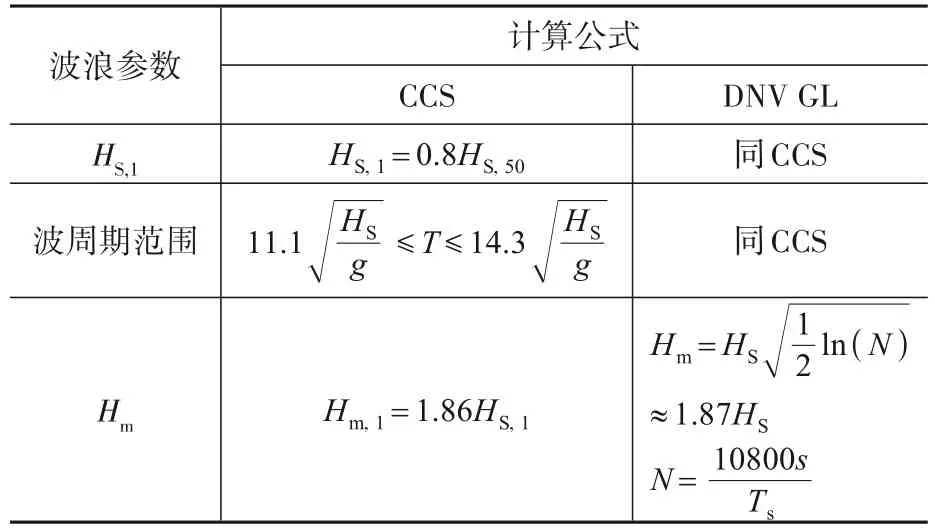
表7 各规范波浪参数计算公式Table 7 Calculation formula of each standard wave parameter

2.2 波浪荷载计算方法

CCS规范与DNV GL规范均采用莫里森公式计算波浪载荷（细长结构，如单桩基础）：

式中：fD为拖曳力分量；fM为惯性力分量；CD为拖曳力系数；CM为惯性力系数；D为柱体直径，ρ为海水密度；u为波浪水质点的水平速度；a为波浪水质点的加速度。

从-d（d为水深，以平均海平面为坐标原点）到波峰η（t）对莫里森方程积分得到作用在圆柱体上的水平波浪荷载：

式中：η（t）为波峰高度；d为水深。

2.2 波浪荷载计算参数的差异

DNV GL规范与CCS规范均提出应当考虑海洋生物的附着对实际柱体直径的影响。DNV GL规范给出了拖曳力系数和惯性力系数的计算过程：

式中：k为表面粗糙度；k/D为相对粗糙度。

对于刚加工且未刷涂层的和刷过油漆的钢材视作光滑，高度锈蚀的钢材和混凝土k取3 mm。海生物生长的情况，k可取5～50 mm。

拖曳力系数按照式（7），KC数计算按照式（8）计算：

式中：Ψ为尾流放大系数，可从DNV GL规范［15］中获取；D为柱体直径；Umax静水位下水质点的最大速度；Ti为波浪周期。

惯性力系数的取值按式（9）：

CCS规范要求水动力系数尽量由试验确定。在实验资料不足的情况，光滑圆形构件的拖曳力系数取0.65，粗糙情况取1.05。对于惯性力系数，光滑圆形构件取1.6，粗糙取1.2。

3 算 例

本文第2节、3节总结了不同规范在风浪荷载计算上的差异，为了充分分析不同规范的差异，本节选取一海上风机工程案例，设置典型的工况，分析规范差异对风浪荷载计算结果的影响。

3.1 工况选择

本文从规范的差异比较和基础设计需求出发，参考Arany等［22］从基础设计角度选出的设计工况，确定本文的设计工况，详见表8和表9。

表8 风荷载计算工况Table 8 Calculation conditions of wind load

表9 波浪荷载计算工况Table 9 Calculation conditions of wave load

3.2 算例计算条件

计算条件包括风机参数、桩基的尺寸、风况条件以及海况条件。表10和表11给出了荷载计算所需要的条件，算例条件参考Arany 提供的参数［22］。

表10 风机及基础条件Table 10 Conditions of wind turbine and foundation

表11 风况与海况条件Table 11 Wind and sea conditions

3.3 风荷载计算结果及比较分析

按照本文2.3节所述计算方法，代入算例参数进行风荷载计算，计算结果如表12、图1和图2所示。

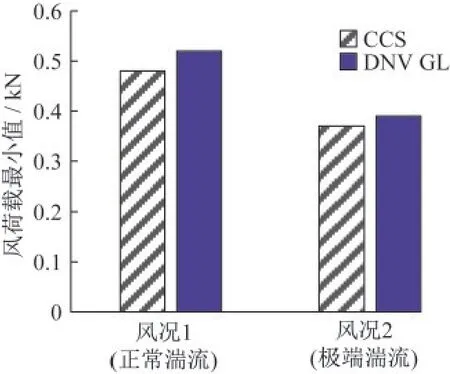
图1 两规范不同风况下风荷载最小值Fig.1 The minimum wind load under different wind conditions in two specifications

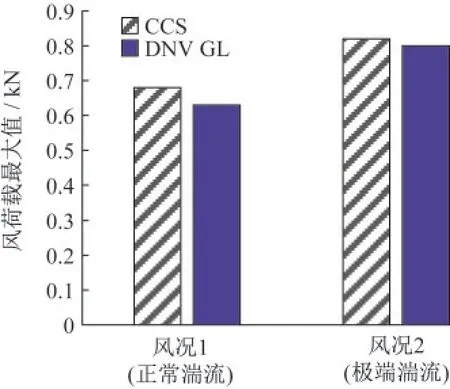
图2 两规范不同风况下风荷载最大值Fig.2 The maximum wind load under different wind conditions in two specifications

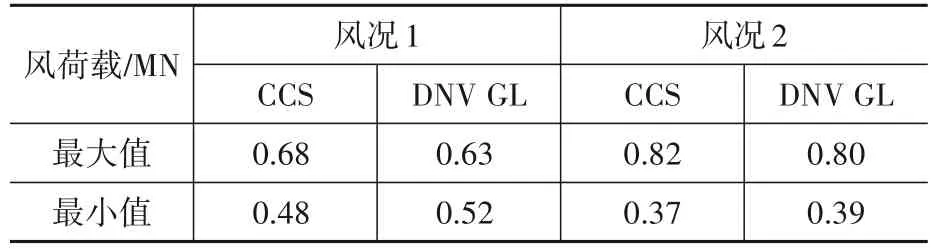
表12 两风况CCS与DNV GL计算结果Table 12 Calculation results of CCS and DNV GL for two wind conditions

由图1与图2可知，在风况1下，CCS规范的风荷载最大值比DNV GL偏大7.9%，CCS规范的风荷载最小值比DNV GL偏小7.7%；在风况2下，CCS规范的风荷载最大值比DNV GL偏大2.5%，CCS规范的风荷载最小值比DNV GL偏小5.1%。差异的原因在于DNV GL规范的湍流标准差计算偏小。

3.4 波浪荷载计算及比较分析

按照第2节所述的计算方法，结合算例条件，进行波浪荷载计算。惯性力分量和拖曳力分量的最大值是出现在波的不同时刻，可以保守地假定惯性力分量和拖曳力分量的最大值之和为波浪荷载，并考虑光滑构件和粗糙构件两种情况，借助Matlab编程完成该部分计算，计算结果见表13、图3和图4。

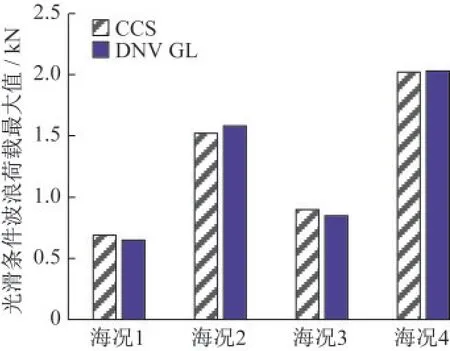
图3 光滑构件两规范波浪荷载最大值Fig.3 The maximum wave load of two specifications for smooth components

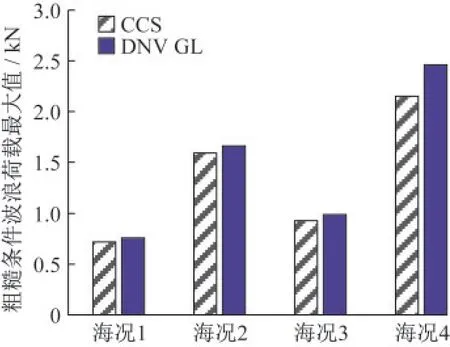
图4 粗糙构件两规范波浪荷载最大值Fig.4 The maximum wave load of two specifications of rough components

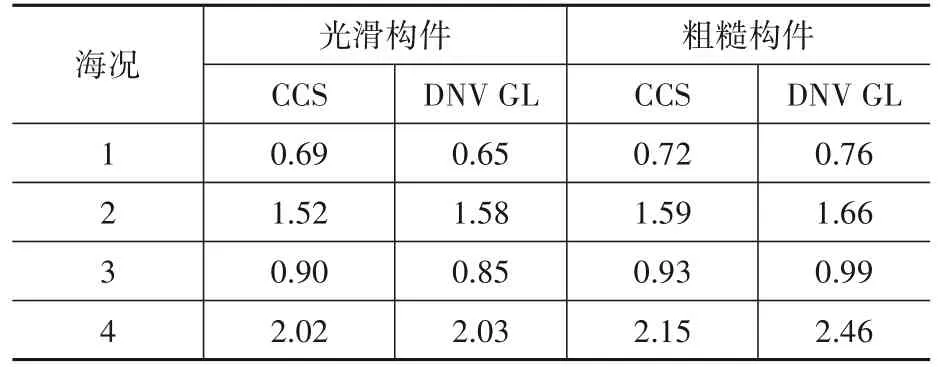
表13 两规范光滑构件波浪荷载计算结果Table 13 Calculation results of wave loads on smooth members in two specifications MN

在光滑构件的情况下，DNV GL规范与CCS规范的计算结果分别为2.03MN和2.02MN，两者差异较小。粗糙构件情况下，DNV GL计算的结果均比CCS的结果大，在4%～14%之间。

图5展示了两规范在粗糙构件情况相比光滑构件的波浪荷载增量。整体上DNV GL的结果要比CCS大。上述差异的原因如前文所述，DNV GL在确定水动力系数的方法上要更细致一些，包含了对雷诺数、波浪周期参数KC数，以及表面粗糙度的考虑。

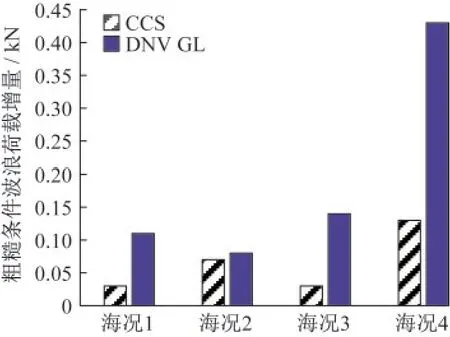
图5 粗糙构件两规范波浪荷载增量Fig.5 Two standard wave load increments of rough component

3.5 风浪荷载叠加

在3.1节工况选择的基础上，考虑到风况条件和海况条件并非独立存在以及风况1、2与海况2、3的组合，对基础设计相关的风浪荷载计算不起控制作用，确定组合工况如表14所示。

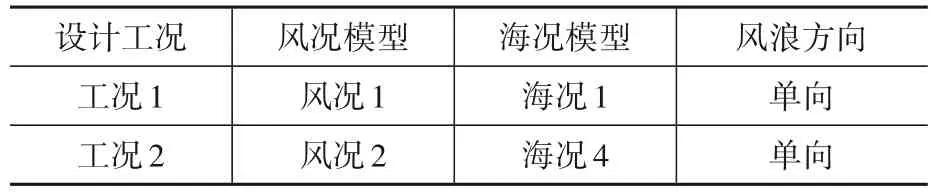
表14 组合工况Table 14 Combined conditions

假设风荷载与波浪荷载的方向一致并线性叠加。根据Arany的研究［23］，这种假设在一般离岸较远的项目是合理的。CCS规范、DNV GL规范与IEC规范的计算结果如表15及图6、图7所示。

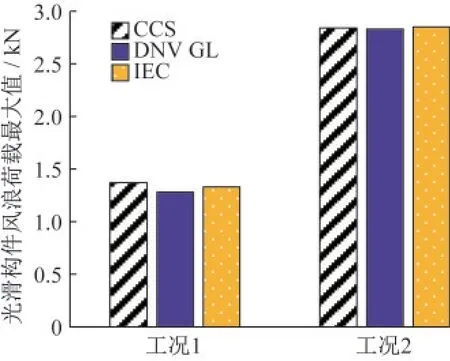
图6 光滑构件风浪荷载最大值Fig.6 The maximum wind and wave load of smooth component

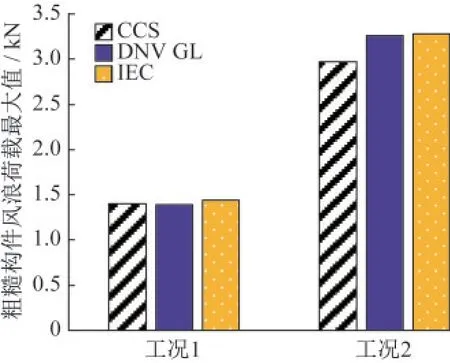
图7 粗糙构件风浪荷载最大值Fig.7 The maximum wind and wave load of rough component

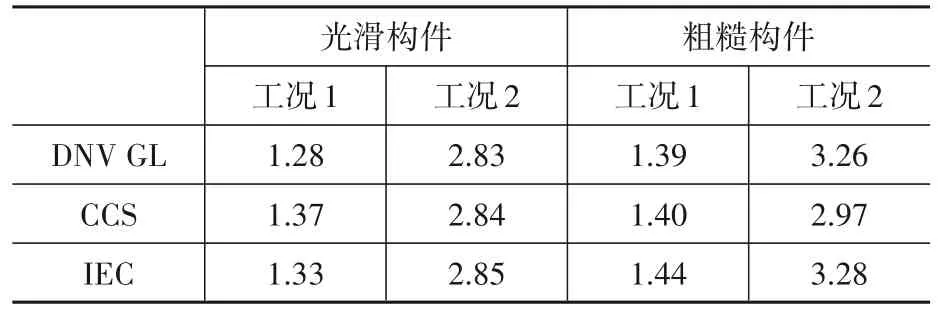
表15 各规范风浪荷载最大值Table 15 The maximum wind wave load of each specification MN

在光滑构件工况1下CCS规范的风浪荷载最大，DNV GL规范最小，IEC规范计算结果介于两者之间，CCS规范比DNV GL规范偏大7.0%；工况2下，三种规范风浪荷载计算结果相差微小。粗糙构件工况1下IEC规范的风浪荷载最大，DNV GL规范最小，CCS规范介于两者之间，IEC规范比DNV GL规范偏大3.6%；在工况2下，CCS规范计算结果最小，IEC规范最大且比CCS规范大10.0%。

4 结 论

本文对CCS、DNV GL及IEC规范的风浪荷载计算思路和参数选取等进行了探讨，通过算例分析了规范差异对风浪荷载计算结果的影响，获得的主要结论如下：

（1） 在正常湍流模型和极端湍流模型中，CCS规范计算得到的湍流标准差相比DNV GL规范偏大，对风湍流考虑偏保守，DNV GL规范针对性考虑了海上风况的湍流条件。关于规范风机等级，建议参考DNV GL规范，针对我国海上风机所面临的风况条件，制定海上风机的等级标准和湍流模型，优化风荷载计算。

（2） 在波浪荷载的计算中，DNV GL和CCS的差异集中在水动力系数上。两者均建议依试验数据确定。在没有试验数据的情况下，DNV GL给出了相对更合理的方法。

（3） 在粗糙构件的情况下，DNV GL得到的波浪荷载最大值比CCS偏大。在波浪荷载计算中，若没有足够的实验数据，建议参考DNV GL规范的水动力系数确定方法。