线性常时滞时变系统的有限时间稳定性分析❋
陈 珂, 张丽霞, 孙敏慧
(中国海洋大学数学科学学院, 山东 青岛 266100)
有限时间稳定是非常经典的数学概念[1-4],该概念可以追溯到20世纪60年代,在1961年首次被提出[1]。在随后的研究中,有限时间稳定性理论逐渐受到学者们的广泛关注。在一些工程领域,如航空航天控制系统、采样控制系统和机械控制系统,有限时间稳定有着非常广泛的应用[5-8]。
目前,有限时间稳定性理论大概可以分为两类:一类是由Bhat和Bernstein提出的有限时间收敛性[9],有限时间收敛理论表明,在系统满足Lyapunov渐近稳定性的前提下,系统状态在一个相对有限的周期内收敛到平衡点[10-11];另一种类型的有限时间稳定性理论是由Amato等[12]提出的,根据该理论,如果初始状态是范数有界的,则系统的状态在给定的有限时间区间内不超过预定的边界。本文研究的是第二种类型。
有限时间有界性理论表明,如果初始状态和外部输入是有界的,则系统状态在预先给定的有限周期内不会超过预定的边界[13-15],因此,有限时间稳定是有限时间有界的一种特例。文献[16-17]研究了异步切换系统的输入-输出有限时间稳定性问题。Amato 和Ariola将上述方法推广到线性离散系统中,得出了输出反馈控制器的设计条件[18]。Van Mellaer对随机系统的有限时间稳定控制进行了研究[19]。之后,又有大批学者取得了有关有限时间稳定性的显著成果,文献[20]研究了时滞跳变系统的有限时间稳定性问题,文献[21-22]研究了带有增益控制的有限时间有界性问题。虽然有限时间稳定性的相关研究已取得了丰富的研究成果,然而这些结果主要集中在线性定常系统,而对线性时变系统还较少检索到相关的研究工作。
本文在前人研究的基础上,将有限时间稳定性理论推广到线性常时滞时变系统。首先,通过选取合适的Lyapunov泛函,以时变的矩阵不等式形式给出有限时间稳定的充分条件;其次,提出了状态反馈控制器的设计方法;最后,通过仿真算例验证了这种控制器的可行性。

1 问题描述与预备知识
考虑如下线性连续常时滞时变系统:
(1)

定义1给定标量c1
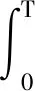
(2)
有
max{xT(s)Rx(s)}≤c1,s∈[-d,0]⟹
xT(t)Rx(t)≤c2,∀t∈[0,T]。
(3)
定义2对于给定常数T>0,矩阵S1>0,S2>0,称系统(1)关于(T,S1,S2)是输入-输出有限时间稳定的,如果在零初始条件下,对于扰动输入w(t),系统满足

(4)
问题描述:对于系统(1),给定正数c1,c2,T,其中c1
u(t)=K(t)x(t),
(5)
使得闭环系统
(6)

2 主要结论
2.1 有限时间有界
本小节主要考虑当u(t)=0时系统(1)的有限时间有界性,主要结果由以下定理给出。
定理1(有限时间有界的充分条件) 给定正数c1,c2,T,其中c1
(7)
(8)
(9)

证明 选取Lyapunov泛函为
则V(x(t))沿着系统(1)求导,可得:


根据定理条件(7)则有
即
将不等式的两边同时乘以e-αt,可得
将上述不等式从0到t进行积分可得

注意到α>0,我们可得

即
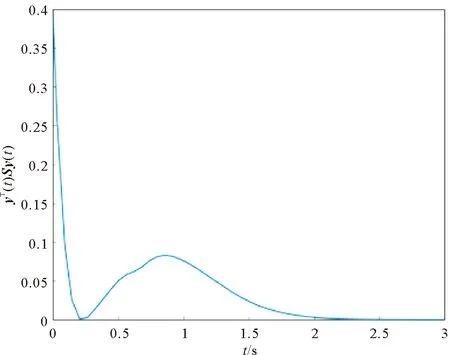
V(x(t)) 则由上式可得 λmin(Q1(t))xT(t)Rx(t)< 因此 xT(t)Rx(t)< c2,∀t∈[0,T]。 由定义1可知,当u(t)=0时系统(1)关于(c1,c2,T,R,S1)是有限时间有界的。 本小节主要研究系统(1)的输入-输出有限时间稳定性,主要结果由以下定理给出。 定理2(输入-输出有限时间稳定的充分条件) 给定标量T>0,矩阵S1>0,S2>0,当u(t)=0时系统(1)关于(T,S1,S2)是输入-输出有限时间稳定的,如果存在标量α>0,β>0与正定对称矩阵Q1(t),Q2(t)∈Rn×n,∀t∈[0,T]满足公式(7)、(9)及以下条件: (10) βeαT≤1, (11) 证明 选取Lyapunov泛函为 由定理1的证明可知 注意到零初始条件,可得 则有 yT(t)S2y(t)=xT(t)CT(t)S2C(t)x(t)≤ 故 yT(t)S2y(t)<1。 由定义2可知,当u(t)=0时线性常时滞系统(1)关于(T,S1,S2)是输入-输出有限时间稳定的。 本小节将根据以上的定理条件,给出闭环系统控制器(5)的设计方法。 定理3如果存在标量α>0,β>0,Q1(t)>0,Q2(t)>0和矩阵L(t)∈Rn×n,∀t∈[0,T],满足(8)—(11)式及以下条件: (12) 则存在状态反馈控制器(5),使得闭环系统(6)关于(c1,c2,T,R,S1)是有限时间有界且关于(T,S1,S2)是输入输出有限时间稳定的,其中, (13) 由(8),(9),(12)式及定理1可知,闭环系统(6)是有限时间有界的,由(10)—(12) 式及定理2知闭环系统(6)是输入-输出有限时间稳定的。 本节中,我们将给出一个数值例子来说明所给结果的有效性。 考虑线性系统(1),参数如下: 图1 开环系统的x(t)的轨迹 通过定理3,我们设计了一个使系统有限时间稳定的状态反馈控制器,图2即为状态反馈控制器的时间轨迹。由图3、4、5可知,在状态反馈控制器下,系统在0~3 s内满足xT(t)Rx(t)≤3,yT(t)S2y(t)≤1,从而是有限时间有界且输入-输出有限时间稳定的。 图2 控制器K(t)的变化轨迹 图3 闭环系统的x(t)的轨迹 图4 闭环系统的xT(t)Rx(t)的轨迹 图5 闭环系统的yT(t)Sy(t)的轨迹 本文通过构造Lyapunov泛函,给出了线性常时滞时变系统有限时间有界和输入-输出有限时间稳定的充分性条件,并设计了状态反馈控制器,最后通过仿真算例验证了定理条件的有效性。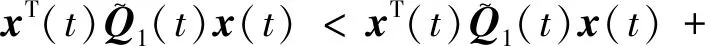
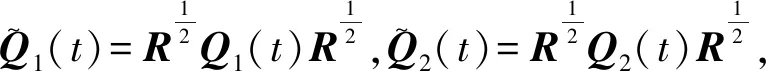


2.2 输入-输出有限时间稳定
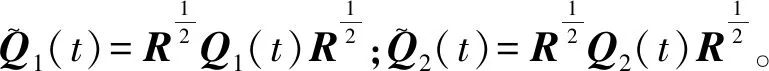




2.3 控制器设计
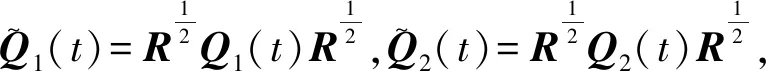
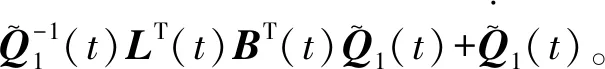

3 仿真举例




4 结语

