基于风浪平衡域理论的浅水情形拖曳系数研究❋

李墨馨, 赵栋梁

(中国海洋大学海洋与大气学院, 山东 青岛 266100)

海面风应力即为海-气界面的动量通量,反映了在海洋与大气的界面处两层流体间的摩擦拖曳作用,是海洋动力模式与海-气耦合模式的关键和基础,对研究全球气候变化和防范极端灾害天气有着重要的科学意义和应用价值。

海面风应力理论上由大气的湍流运动所导致,在大气常通量层以内、波边界层以上[1],可直接由超声风速仪观测的湍流脉动值经涡动相关法计算求得。然而在实际应用中,风速的观测值通常为某一固定高度处大气运动的平均流速,故人们引入拖曳系数CD这一概念,将海面风应力τ写为:

(1)

式中:ρ是空气密度;u*是空气摩擦速度;U10是海面以上10 m处的风速。当大气层结接近于中性稳定状态时,常通量层内的风速廓线关系式可以写为:

(2)

式中:κ = 0.4是von Kármán常数;z是距离海面的高度;Uz是对应高度的风速;z0是海面粗糙度。

过去几十年中,人们进行了许多针对拖曳系数的研究,最开始拖曳系数被取为常数,而后拖曳系数被描述为随风速增大的函数,近些年人们发现,拖曳系数并不是随着风速的增大而持续增大的,当风速大于某一特定值时,拖曳系数开始下降或趋于平缓,此时的风速被称为临界风速U10c(Critical wind speed)。图 1展示了前人给出的临界风速,它们被分为了三类,分别属于实验室风-浪水槽[2-7]、近岸海域[8-12]和开阔大洋[13-23]。一些研究认为拖曳系数随风速变化的同时也与水深相关联[24-28],其中Makin 和 Kudryavtsev[26]与Zhao等[11]指出浅海的拖曳系数大于深海的拖曳系数;同时Zhao等[11]指出,浅海的拖曳系数临界风速比深海更小。图 1显示,相比浅水情形下的风-浪水槽和近岸海域,深水情形下的开阔大洋中可以观测到更大的临界风速;然而,不论在何种情形下,人们观测到的临界风速都是在一定风速范围内变化的。由此可见,拖曳系数是否对水深存在依赖性,并且,水深是否是影响拖曳系数临界风速变化的直接因素,这些问题都有待解答。

图1 不同研究者给出的拖曳系数趋于饱和的临界风速

本文围绕浅水情形下水深对拖曳系数的影响展开探究,使用大陆架之上水深在10～320 m之间变化的美国东海岸国家数据浮标中心(National Data Buoy Center,NDBC)业务化浮标观测数据,基于风浪谱的平衡域理论反推得到摩擦速度,针对水深对拖曳系数的影响尚存的问题进行讨论并给出合理解释。

1 数据介绍

NDBC业务化浮标可以提供长时间、大范围的风速、海浪、气温和水温的同步观测数据。本文使用的NDBC浮标数据下载于NOAA的FTP服务器,其地址为ftp://ftp-oceans.ncei.noaa.gov/pub/data.nodc/ndbc/,时间跨度为2011年1月—2020年12月,空间分布范围如图 2所示。本文所用浮标的风速计和气温传感器均位于海面以上约5 m高度处。

(蓝色圆圈代表浮标。Blue circles represent the buoys.)

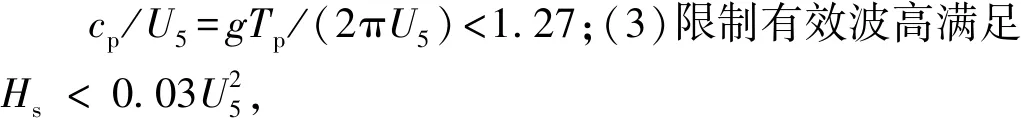
(3)

选择了Ri的绝对值小于0.003的大气稳定度接近于中性稳定的数据,避免了大气稳定性对海面风应力与海浪发展的影响,使公式(2)得以成立。公式(3)中:zt是气温的测量高度;z是风速U的测量高度;Ta和Tw分别是海面气温和水温,单位是摄氏度,这里的zt与z均为5 m。

本文将上述筛选出的大气中性稳定时风浪状态下的数据按水深由小到大划分为5个档次,具体信息如表1所示。本文后续内容皆以表1中的平均水深指示数据结果的水深划分。

表1 大西洋沿岸浮标水深数据信息

2 方法介绍

公式(1)中的摩擦速度可以由海浪能量密度谱基于风浪谱的平衡域理论反推得到[30-31]。Toba[32]和Phillips[33]指出,风浪谱在平衡域内具有正比于f-4的谱型,且其表达式为:

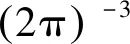
(4)

式中:αT被称为Toba常数;f为频率;S(f)为海浪能量密度。在保证平衡域位置不被移动的同时,为了减小海浪观测仪器和谱估计方法固有缺陷所带来的数据波动,本文分别将5组不同水深的风浪谱数据按相同谱峰周期Tp、相同风速区间求平均,并围绕平均谱进行分析。图 3展示了部分平均谱,其纵轴为海浪谱谱值S(f)与频率f四次方的乘积。从图中可以清晰地看到,在海浪谱的谱峰频率之后存在着平行于横轴的平衡域。依据Kuik等[34]和Thomson等[30]给出的方法,Toba常数αT可由NDBC浮标的海浪方向谱数据计算得到,其结果(见图 4)显示,Toba常数的值集中于0.106。如此,已知平衡域内的海浪谱和Toba常数αT,摩擦速度u*便可由公式(4)反推得到,同时,联立公式(1)和公式(2)便可得到拖曳系数CD。

(图例指示不同的水深。红色粗直线指示S(f)正比于f-4,蓝色粗直线指示S(f)正比于f-5。 The legend indicates different water depths. Red thick line represents S(f) is proportional to f-4 and blue thick line represents S(f) is proportional to f-5.)

(圆点为原始值,菱形为平均值。Dots are raw data and diamonds are average data.)

3 不同水深的拖曳系数

依照上一节所述方法,本文得到了风浪状态下美国东部沿岸海域不同水深下的摩擦速度和拖曳系数。

图 5展示了五组不同水深下的摩擦速度u*随观测风速U5的变化,图中以不同的颜色区分不同的谱峰周期Tp。从图中可以看到,摩擦速度随着风速的增大而增大,这与人们的普遍认识相同。同时由图 5还可看到,不论在整体上还是在相同风速的限定下,摩擦速度均随着谱峰周期的增大而增大。图 6展示了不同水深的拖曳系数CD随风速U10的变化,对于平均水深为22、40、59和82 m的这四组数据,其最大风速均略大于20 m/s,拖曳系数整体上均随风速的增大而增大,此趋势在图 7中亦可体现。对于平均水深为231 m的这组数据,其最大风速可以达到近30 m/s,拖曳系数在整体上呈现出先增大后减小的趋势,其临界风速约为24 m/s,此趋势在图 7中清晰可辨。对水深而言,这5组数据的拖曳系数并未有明显不同。从图 8中可以看到,不同水深拖曳系数的平均值几乎是一致的,且其值约为1.3×10-3,这与Rossby 和 Montgomery[35]将拖曳系数取为常数的结果完全相同。

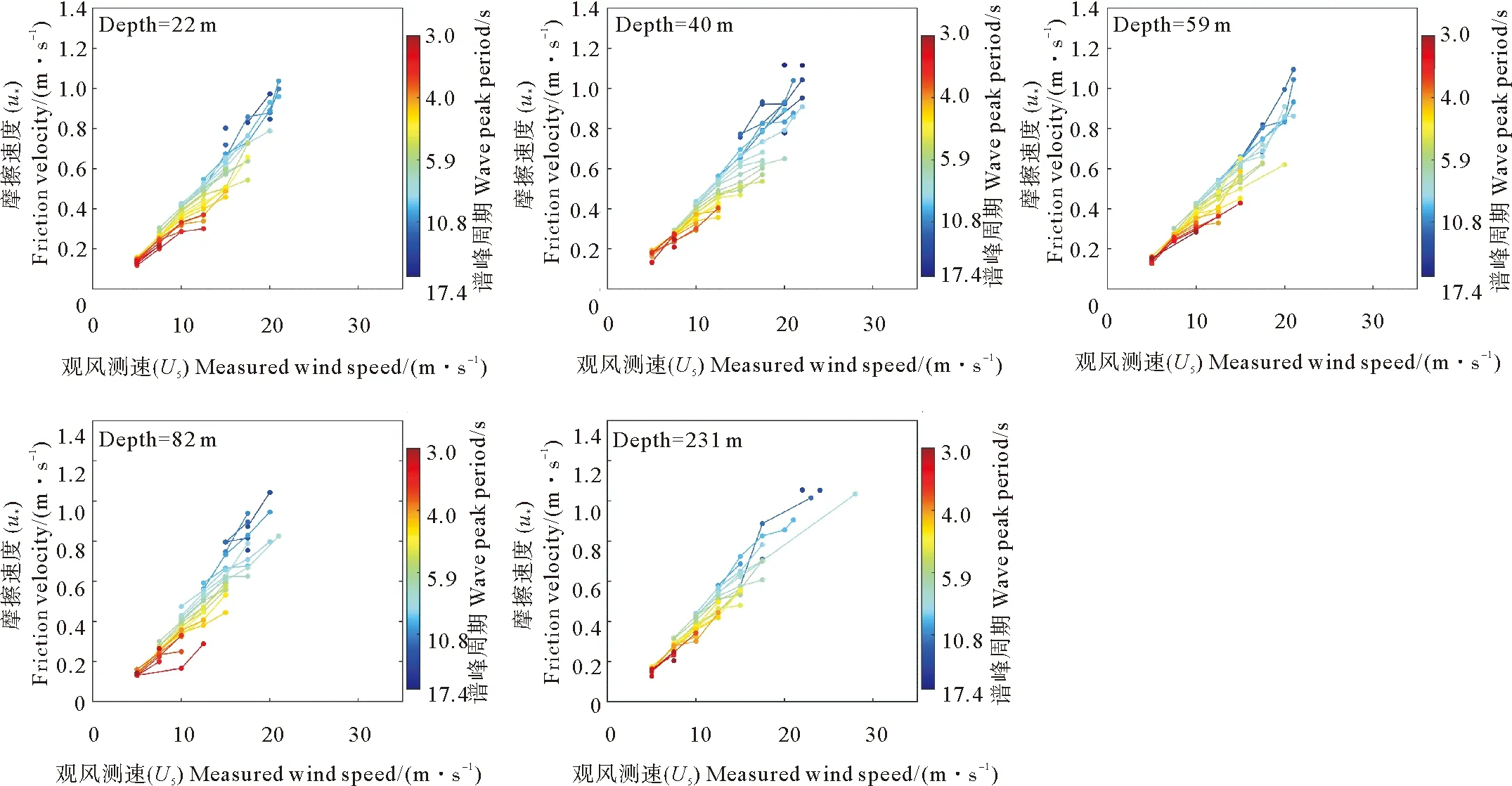
图5 不同水深的摩擦速度(u*)随观测风速(U5)的变化

上述结果表明,在海浪状态为风浪时,水深的不同并不会导致拖曳系数发生明显改变,因此,导致前人的拖曳系数结果在不同水深下显著不同的直接原因并非水深的不同,应另有其他。值得格外注意的是,图 6中,在谱峰周期相同的条件下,具有较大风速跨度的拖曳系数会呈现出随风速增大而先增大后减小的变化趋势,并且随着谱峰周期的增大,在相同谱峰周期条件下,拖曳系数随风速变化的临界风速也会增大。由此本文推测,导致不同水深条件下拖曳系数随风速的变化呈现不同结果的直接影响因素或为与谱峰周期相关的海浪参量。

4 分析和讨论

本文所用数据与前人的拖曳系数相关研究相较具有时间跨度大、空间范围广的特点和同时涵盖大量不同状态风浪谱观测数据的优势,这为我们以全新的角度探究不同水深情形下拖曳系数与海浪参量的关系提供了重要基础。正是在这一基础之上,本文呈现的结果表明,水深不是直接影响拖曳系数的因素,而海浪谱的谱峰周期与拖曳系数的变化规律之间有着紧密的关联。

为了解释前人的研究中,拖曳系数在不同的水深下呈现出不同状态的问题,本文引入谱宽度这一概念。谱宽度代表的是海浪能量在频域上的集中程度,谱宽度的值越大,风浪的能量便会分布在一个越宽的频域范围内,即谱宽度越大能量越分散,谱宽度越小能量越集中。Cartwright 和 Longuet-Higgins[36]给出了一个谱宽度的定义:

(5)

此外另一个谱宽度的定义为:

(6)

公式(5)和(6)中的m0、m1、m2和m4为不同的海浪谱阶矩,其定义为:

(7)

因为谱宽度ε和谱宽度ν在本质上并无区别,它们代表的物理含义是相同的,故本文只以谱宽度ε为例进行讨论。

图6表明,在不同水深下,拖曳系数随风速的变化规律与谱峰周期有关,而图 9显示,谱峰周期的大小决定着谱宽度的大小,且谱宽度的大小与水深无关。图 10结果显示,不同水深下,拖曳系数随谱宽度的变化均收敛于同一条拟合关系式,即图中的黑色曲线,该关系式来自于包含湖泊、近岸和大洋的NDBC浮标数据结果,在图 10中仅作为一个对比不同水深结果的标尺。图 6中,拖曳系数随风速的变化因谱峰周期的不同而呈现较大的离散状态,然而图 10中,拖曳系数随谱宽度的变化则呈现较好的收敛状态,且不论水深如何变化,拖曳系数随谱宽度的变化规律均相同。

图7 不同水深下拖曳系数的平均值随风速的变化

图8 拖曳系数(CD)随水深的变化

图9 谱宽度(ε)与谱峰周期(Tp)的关系

图10 拖曳系数(CD)随谱宽度(ε)的变化

基于上述结果,本文认为海面风应力拖曳系数的大小依赖于海-气界面处海表面的波动状态,即拖曳系数大小的直接影响因素应为海浪的谱宽度。具体而言,随着谱峰周期的增大,风浪越成长,风浪的组成波越多,海浪的谱宽度将越大,这意味着有更多的海浪组成波参与海-气相互作用过程,使得海-气耦合强度增大,并且表现为拖曳系数随海浪谱宽度的增大而单调增大。当谱宽度或谱峰周期达到最大值时,拖曳系数也将达到其海浪系统背景下的最大值,此时对应的风速即为临界风速。前人的研究中,不同水深下的拖曳系数呈现出不同的状态也是源于其观测结果所处的海浪系统背景不同,当近岸的水深较浅时,浅水效应引起的波浪破碎通常会限制长波的存在,使谱宽度减小,从而使临界风速相对于水深较大处有减小的趋势,但水深较大并不一定意味着大的临界风速,而是由具体的谱宽度大小来决定。

5 结语

本文使用时间跨度大、空间范围广的沿岸浮标数据,基于风浪谱平衡域理论推算得到海面风应力拖曳系数围绕浅水情形下不同水深的拖曳系数变化规律进行了探讨,其结果发现:水深不是引起拖曳系数变化的直接因素,拖曳系数随风速的变化因谱峰周期的不同而呈离散状态,在不同水深条件下,拖曳系数与海浪的谱宽度之间均具有一致的紧密关联,并进一步使用谱宽度的相关理论解释了前人给出的拖曳系数在不同水深下呈现不同变化规律的原因。

本文的研究成果对于合理地参数化海面风应力拖曳系数具有重要的引导意义。然而,基于平衡域理论的拖曳系数推算方法将本文的结果限制于风浪状态下,但依据谱宽度的概念,拖曳系数与谱宽度之间的关联性对于解释涌浪背景下不同水深的拖曳系数应同样适用,此观点仍需进一步的工作来验证。此外,本文所聚焦的海浪周期为谱峰周期,相较而言,平均周期具有更稳定的特点,未来应将关于平均周期的讨论一并纳入其中。