非荷载因素作用下超静定结构的力学特性分析

马 骏

（渤海大学，辽宁 锦州 121013）

0 引言

对于非荷载因素对超静定结构影响的研究，到目前为止已经有很多成熟的方法和理论，大部分都已作为知识点编入教材。而这些方法理论中有些传统经典，也有些新颖易用。如李增福等[1]研究的超静定结构如何求解位移，其方法是先将具有多余约束的超静定结构转化成无多余约束的静定结构，这样就把问题通过传统的思维方法化繁为简。李忠芳等[2]对温度应力问题进行深度剖析，融合重组成一个关于构件会自由膨胀的静定问题和关于装配应力的超静定问题。王树范等[3]在解决支座移动给超静定结构带来的影响时，通过等效思维，将支座的移动作用等效成外部荷载，然后再求解超静定结构的内力。本文利用力法原理分析非荷载因素（温度、支座移动等）在超静定结构上表现的力学特性。

1 力法原理求解超静定结构内力公式

力法是超静定结构求解方法中最基本的方法。例如温度改变后，求超静定的内力，可以把典型方程中的Δip改成由于温度差所引起的、与多余约束未知力Xip相对应的位移Δit即可。这时典型方程就变为：

上面式子各系数算法与传统方法基本一致。其不同点在于Δit的求解，还有对位移协调方程等式中右边的位移Δi的注意。其中Δit是关于静定结构因温度变化而发生的位移，可通过下式解决：

式中：

α——材料的线膨胀系数。

后者Δit则要看上述公式是用于哪种非荷载因素情况。当然，此处是温度荷载，其在建立力法的基本结构中不产生位移，故而取0。以上为力法求解温度荷载在超静定结构中的影响，力法对于求解支座移动对超静定结构中所产生的影响同样可以利用上式[4-5]。只是此时的Δit是在支座移动情况下产生的位移，其求解方法利用如下公式：

而方程右端的Δi则不再是0，而是条件中对应处的实际位移。非荷载因素下超静定结构的求解问题，温度因素和支座移动因素是非荷载因素的典型代表，本文主要针对这两种因素的影响给予说明。当然，因制造带来的误差而导致的影响也重要。其位移可以通过位移求解的一般公式得到，公式如下：

上式通用于超静定与静定，使用时根据实际情况对应代入，无则取零。

除了力法可以解决非荷载因素的问题，位移法、能量法等也可以。本文主要例举利用力法原理介绍非荷载因素（温度、支座移动等）在超静定结构上表现的力学特性。

2 温度变化

图1(a)所示为一跨刚架，刚架内侧温度+10℃，外侧+20℃。求解其弯矩并绘出弯矩图。截面为矩形，高度h=l/10，线膨胀系数为α[6]。

图1 温度荷载作用下的刚架

求解过程如下：

（1）首先由图1(a)可知此结构温度的分布和结构体都是对称的。所以利用这个特点对其简化，得图1（b）。此时半结构中只剩下未知力X1和X2。

（2）列力法基本方程：

δ11X1+δ12X2 +Δ1t =0

δ21X1+δ22X2 +Δ2t =0

（3）求系数。由图1(c)、(d)通过图乘得：

按照图1(a)计算自由项：

（4）最后将上述值对应回代方程，有：

2 支座移动

如图2(a)所示，一根超静定梁，A端下沉距离a，试绘制其弯矩内力图[7]。

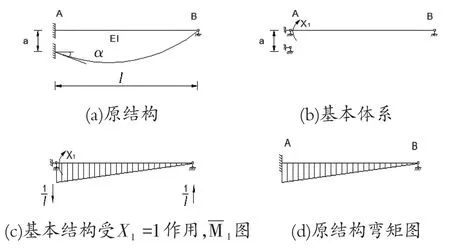
图2 支座移动作用下的刚架

求解过程如下：

对原结构图观察，此梁有一个多余约束，其基本结构如图2(b)所示，列方程为：

δ11X1+Δ1c=Δ1

根据已知条件，梁A端的转角Δ1=φ；X1=1作用下基本结构的相应转角可由图2(c)求得，即A端转角由刚体位移关系求得。Δ1c也可按照图2(c)，利用单位荷载法求得。

将上述所求的常数项和相应的系数代入力法基本方程，从而解得：

综上绘制弯矩图，如图2（d）所示。

3 支座移动与温度变化同时作用

前文介绍了利用力法原理求解非荷载因素下超静定结构的内力，这里介绍利用能量原理的办法解之。如图3(a)所示为一根等截面梁高h，材料为线性弹性体，材料线膨胀系数α。试用余能原理解其内力[8-9]。

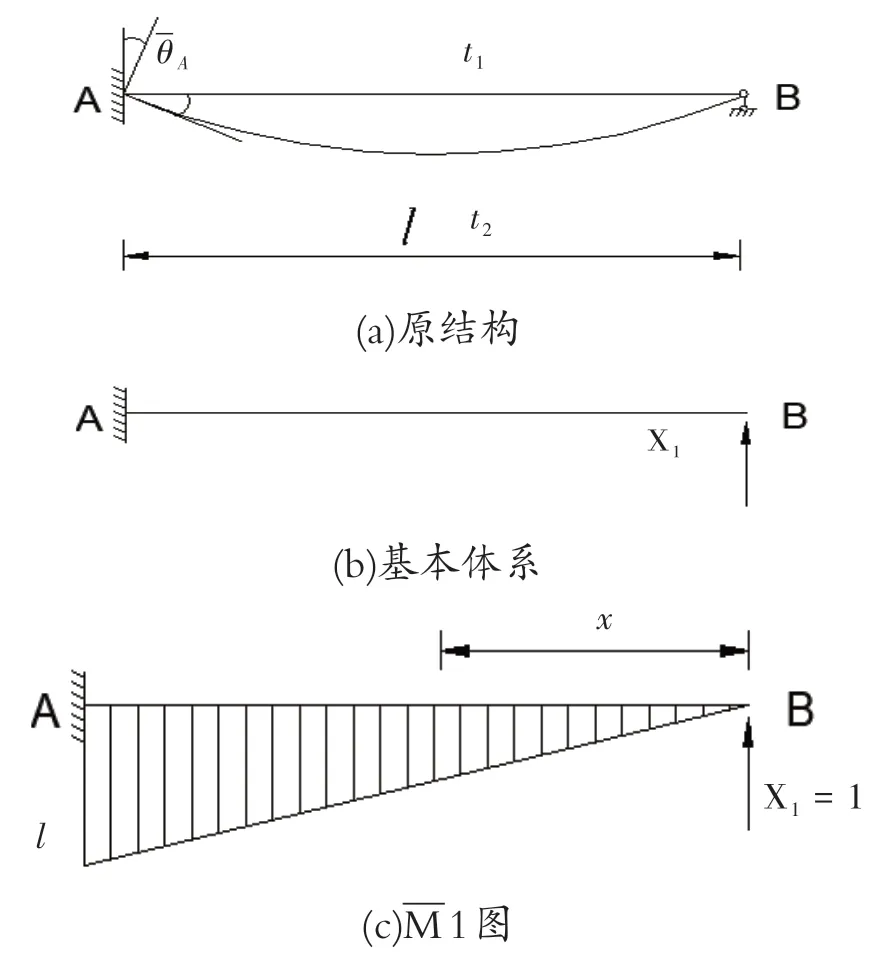
图3 支座移动作用下的刚架

求解过程如下：

（1）确定静力可能内力，由图3(b)、(c)得：

（2）求结构余能Ec：

（3）应用余能驻值条件：

因此：

4 结束语

通过以上例题推演，可以发现，在非荷载因素作用的情况下，超静定结构会产生内力。静定结构没有多余约束，即它的自由度刚好为零，其上所有约束都参与维持它的平衡状态。所以无论哪个约束移动，结构都会随之移动从而去实现自平衡，这样就没有结构构件的变形，自然也就不会产生自内力。而超静定结构有多余约束，约束之间相互牵制，无论哪一个都是不能随便移动的，除非让构件产生变形。而有变形就会有力，所以无论是温度改变也好、支座移动也好，亦或者是制造误差、材料收缩等，只要能使超静定结构发生形变的因素，均可使超静定结构产生自内力。这样，材料的强度在结构投入使用之前就已经被消耗一部分了。若从此角度来看，某些情况下，静定结构反而会更加适合某种严格控制自内力工程的应用。但一般工程都是超静定结构，因为要保证它的安全储备，不可以被轻易毁坏。因此这也给工程师们尤其是施工人员一个重要的提示，为了避免工程结构自内力的产生，在施工过程中一定严格把好施工质量关，对于建筑基础、构件的制造等要格外注意。