基于社会网络分析法的高中生化学认知结构研究

李巧　周青

摘要： 采用社会网络分析法测查高中生“物质的量”主题的认知结构，发现气体摩尔体积、物质的量浓度、阿伏伽德罗常数为核心节点，是展开深入学习的基础，“一定物质的量浓度溶液的配制”是学生突破学习瓶颈的关键。学困生在知识分类和存储时存在障碍，其转化可从摩尔质量、气体摩尔体积着手，落实基本概念；中等生提高应关注气体摩尔体积、阿伏伽德罗定律，重视证据推理能力。

关键词： 认知结构； 社会网络分析； 中心性； 结构洞； 物质的量

文章编号： 10056629（2023）10001707 中图分类号： G633.8文献标识码： B

认知结构是个体在固定知识范围内的全部观念和组织［1］，对认知结构的研究聚焦于“知识”和“知识的组织”［2］。学习实际上是不断扩大和完善个体认知结构的过程。不同学习能力的学生，对知识的理解程度和建构过程有差异。研究不同学习者的认知结构对诊断学习困难、实现以学定教具有指导意义。

1 研究背景和意义

研究者倾向于使用图形来表征认知结构，这种图形包括标有概念的“点”和连接点的“线”［3］。从最初的树状图发展为概念图，到后来广泛使用的流程图（Flow Map），认知结构的研究方法不断精细化。然而，以上方法着重表征个体数据，群体特征分析略有不足。由此，Yang［4］等人试图将社会网络分析法（Social Network Analysis，简称SNA）［5］运用于认知结构测查。

社会网络是由节点（社会行动者）和连线（代表行动者之间的关系）组成的整体，认知结构和社会网络具有一定的相似性。社會网络分析法在教育研究中的优势显著［6，7］：网络分析的重点不是独立的个体，而是内部的组织关系；网络分析的对象不是一个单独的样本，而是一个相互联系的整体；网络分析角度不止有定性分析，还有定量分析，如中心性、结构洞、块模型等。孙丹丹［8］、张燕清［9］等人应用社会网络分析法研究优等生群体的数学认知结构，发现良好的数学认知结构节点密集、联系紧密、结构洞少。

物质的量是高中化学计算的基础，中学化学由此进入定量研究的新阶段。已有研究指出“物质的量”“摩尔”“阿伏伽德罗常数”等概念“拗口难懂”，学生也普遍反映知识点抽象、难懂难记，大部分学生处于“部分理解”夹杂着“错误理解”的水平，在物质的量、气体摩尔体积和物质的量浓度上的迷思概念较多［10，11］。也从不同角度表明“概念认识相对割裂、知识网络不成体系”是该主题下学习困难产生的重要原因。研究者提出构建以“物质的量”为中心的概念模型，外显和强化核心概念之间的逻辑关系，加强结构化认识可有效应对以上学习问题［12］。已有“物质的量”学习困难测查主要以个体形式或整体形式展开，缺乏对不同学生群体的比较研究。

因此，本文采用社会网络分析法测查学生“物质的量”主题的认知结构，前期选择半结构化访谈收集数据，最大程度地减少认知结构表达过程中的干扰，以期从学生角度为实际教学提供参考。

2 研究方法

2.1 研究对象

选取陕西省某中学高一（1）班、高一（2）班学生为研究对象，该校为西安市民办普通高中，整体处于全市中等水平，所选班级为平行班，学生成绩属于校内中等层次。参照最近两次测试的平均成绩选出三组学生，每组15人，共45人，其中男生24人，女生21人，每组学生的平均成绩差值为20分左右。

2.2 社会网络分析

2.2.1 认知结构的引出

当学生完成“物质的量”学习内容之后的一周内进行半结构化访谈，提出三个不带有任何提示性和引导性的问题：（1）关于“物质的量”你能想到哪些知识点或概念？（2）你能否具体描述一下上述知识点？（3）你所描述的知识点或概念之间有什么联系？即时录音［13］。

2.2.2 认知结构的外显

将访谈得到的录音数据转化为文本，划分“节点”和“关系”。“节点”为知识点所涉及的名词或名词短语。依据层级语义网络模型，概念之间是有“关系”的，包括从属关系和相关关系等。

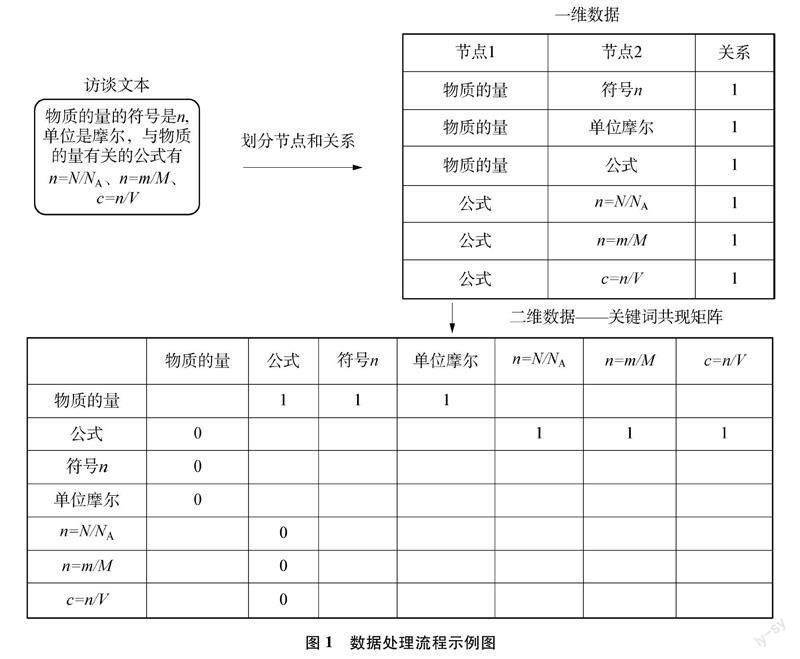
例如有描述文本：“物质的量的符号是n，单位是摩尔，与物质的量有关的公式有：n=N/NA、 n=m/M、 c=n/V”，则节点有：物质的量、符号n、单位摩尔、公式、n=N/NA、 n=m/M。学生由物质的量直接联系到符号n、单位摩尔、公式，由公式联系到n=N/NA、 n=m/M、 c=n/V，即“物质的量”和“符号n”关系记为“1”，“物质的量”和“单位摩尔”关系记为“1”，“物质的量”和“公式”关系记为“1”，“公式”和“n=N/NA”关系记为“1”，“公式”和“n=m/M”关系记为“1”，“公式”和“c=n/V”关系记为“1”。

“1”表示两个节点之间有关系，重复出现多次的“关系”不累计。此外，确定节点时专有名词、公式不拆分；要统一标准，表示同一意思的词语应划分为相同的节点，如标准状况、标况等描述应划分为“标准状况”节点；单位、符号等没有确定意义的名词不单独列出，与具体名称或字母连用，如单位摩尔、符号M。最终获得包含每位学生的“节点”及“关系”的一维数据表格。

然后，使用Power Query将一维数据对称化，转化为二维数据——关键词共现矩阵，矩阵中“行”和“列”内容一致，包含学生提到的所有节点，单元格中的数字代表两个词语之间的关系。上述数据处理流程如图1所示。

正式分析文本之前，从学优生、中等生、学困生中各随机选取一个访谈文本，由笔者和另外一名研究者进行背对背分析［14，15］。以学生X为例，两位研究者划分的节点数为65和60，相同的节点是60，则节点编码信度为（60+60）/（65+60）=0.96；分别以两位研究者所划分的节点构建关键词共现矩阵，产生的关系数为79和65，其中相同的关系为58，则关系编码信度为（58+58）/（79+61）=0.83。试测后，结合“物质的量”内容特点，商讨和补充更为详细的编码规则，节点编码信度和关系编码信度分别为0.92和0.84，较为符合研究需要。之后，由笔者统一对全部数据进行处理，获得45个样本的关键词共现矩阵，存储为Excel。

2.2.3 认知结构的表征

将每组学生的15个矩阵进行叠加汇总，得到学优生、中等生、学困生3个矩阵。依次将3个矩阵导入Ucinet6.0获得后缀为“.##d”“.##h”的两个文件，用Ucinet6.0打开“.##h”文件即可得到三个学生群体的中心性、结构洞、块模型数据。

（1） 中心性。

“点度中心性”指的是与某一节点有直接关系的其他节点的数目，点度中心性的值越大，说明该节点越处于中心地位。在社会网络中，该点具有较高的“权力”，在认知结构中，该点处于核心位置，属于重点知识。如图2所示，点B处于核心位置。

“中间中心性”指某一节点成为其他节点之间“桥梁”的次数。在社会网络中，中间中心性较高的点往往扮演着“中介”或“中间人”的角色。在认知结构中，这些节点连接了该主题下的核心概念与边缘概念，成为学生学习的瓶颈。换言之，如果教师在完成基础教学之后，对中间中心性较高的节点进行重点讲解，将有助于学生强化概念之间的联系，增强认知结构的稳固性。以图2所示的五节点网络关系图为例，点B成为“桥梁”共10次，中间中心性更高，见图3。

“接近中心性”描述了某节点与其他节点的接近程度，以两点间的距离来衡量，其值为路径长度的倒数。接近中心性值越小，接近程度越低，则该节点对其他节点的依赖程度越大。在社会网络中，该节点处于网络的边缘。在认知结构中，掌握该节点需要的知识储备越多。如图3，A、 B、 C、 D、 E点与其他各点的距离之和分别为8、 5、 6、 9、 8，说明点D距离其他各点更远。

（2） 结构洞。

结构洞［16］指的是两个节点之间的“非冗余关系”。在社会网络中，成为结构洞的节点，往往处于信息交流的把控地位。在认知结构中，对结构洞的有效掌握，有利于节点之间产生更丰富的联系，促进形成良好的认知结构。如图4所示，节点F、 D都和C有关，但两者没有直接关系，相当于有一个空洞，这两个节点产生联系必将通过节点C，则C为一个结构洞。点E和点A可以直接产生信息交流，对于B来讲，A与B的关系和E与B的关系则是冗余的，点B不能视为结构洞。

结构洞的数据结果有四个变量，有效规模（EffSize）、效率（Efficie）、限制度（Constra）和等级度（Hierarc），其中，限制度最为重要，某节点限制度越低，所具有的结构洞越多，越处于控制地位。

（3） 块模型。

块模型将初始矩阵中的各点，经过聚类分析算法重排节点，形成结构上对等的像矩阵。简言之，就是将各个节点集中到更大的点集之中，分析认知网络的内在结构。分析块模型可得不同学生群体对知识点的处理方式和归类模式。

3 结果与讨论

3.1 中心性

分析三组学生认知结构中各节点的中心性，点度中心性和中间中心性的值越大，节点特征越明显，而接近中心性值越小，节点特征越明显。现选取具有代表性的前6组结果进行分析，希望获得更为典型的结论。

3.1.1 点度中心性

点度中心性较高的节点如表1所示。三组学生构建的以“物质的量”为中心的知识体系包括气体摩尔体积、物质的量浓度、阿伏伽德罗常数等节点，说明以上节点是学生整体认为的核心概念，当然此结果与授课教师的强调密不可分。

从A组到C组，气体摩尔体积的点度中心性在下降，说明不同程度的学生对气体摩尔体积的认知差异明显。学优生能够联系到气体摩尔体积的取值、单位、适用对象、影响因素等，如：“气体摩尔体积在标准状况下数值为22.4L/mol”；“气体摩尔体积对象必须是气体”；“气体摩尔体积单位是L/mol”；“气体摩爾体积是22.4L/mol的状态不一定是标准状态，可能是温度升高、气压变化，也可能是气压升高、温度变化”，个别学优生由此展开对阿伏伽德罗定律的讨论。而学困生中有9人能联系到n=V/Vm，仅4人谈到“取值”，2人提到“适用对象”。

教师应重视这一差异，改变教学策略促进该知识点的“落地生根”。如先利用温度传感器、压强传感器探究阿伏伽德罗定律，结合数学函数图像理解理想气体状态方程，进而推理出气体摩尔体积，给知识以真实的发生过程，形成对气体摩尔体积的系统认识。

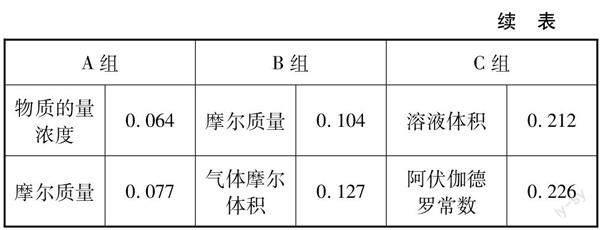
值得关注的是，A、 B组同时将“摩尔质量”节点放在核心位置，从该节点能够联系到摩尔质量的定义、单位、数值、平均摩尔质量、十字交叉法等。C组学生并未回忆起相关内容。学困生的转化可从摩尔质量入手，如设计概念辨析环节，梳理易混淆物理量；围绕“摩尔质量的计算方法”开展主题研讨等。A组学生出现了“溶液配制”节点，说明学优生更加关注知识的实践，中等生提高可从“一定物质的量浓度溶液的配制”着手。

3.1.2 中间中心性

中间中心性较高的节点见表2。三组学生共同的节点为：定容、称量，其他节点如容量瓶、溶解、洗涤，也与溶液配制相关。说明溶液配制是学生认知结构中的重要桥梁，学生通过该节点能够联系到实验仪器、基本操作、误差分析，以及溶液稀释和混合。强化溶液配制内容能加强认知结构的稳固性，印证了“实验是化学的最高法庭”，实验教学不可省略更不可取代。

A组出现“物质的量”节点，B、 C组未出现，反映出学优生的知识结构更加紧密。A组有pV=nRT节点，说明学优生对阿伏伽德罗定律掌握到位。这恰恰说明A组学生“气体摩尔体积”的点度中心性高于另外两组的原因之一，是与阿伏伽德罗定律建立的联系。因此，中等生提高可关注阿伏伽德罗定律。

特别的是，C组学生出现了“摩尔质量”节点，结合访谈文本发现有学生认为摩尔质量分为气体摩尔质量、液体摩尔质量和固体摩尔质量，其混淆了气体摩尔体积和摩尔质量这两个物理量，基础知识不牢固，认知结构的可辨别性差。应加强学困生对“摩尔质量”和“气体摩尔体积”等概念的辨析，这与前文研究结果一致。

3.1.3 接近中心性

从整体来看，接近中心性较低的节点涉及溶液配制过程中的误差分析、仪器名称和基本操作等，如表3，说明相关知识点对核心概念的依赖程度高，需要学生有一定的知识储备。各组的数据表现不尽相同，A组能够结合公式理论推导实验误差，具有较强的学科思维能力和证据推理意识，B组能够回忆起基本操作流程，误差分析认识模糊，说明中等生的提高需加强证据推理能力。

对于C组学生，标准状况，22.4L/mol， 0℃、 101kPa等节点已经处于边缘位置，学生的基础知识储备不足，只能支撑其掌握上述知识点。这也给实际教学提供了方向，对于学困生的转化，不应盲目拓展拔高，一味练难题、讲难题，而应夯实基础，构建最底层、最核心的知识结构，循序渐进。

3.2 结构洞

将不同学生群体的结构洞变量导出，限制度较低的节点如表4。物质的量浓度、摩尔质量限制度较低，具有的结构洞更多，处于绝对的控制地位，是展开更深入学习的基础，实际教学中应重点突破。A、 B组认知结构中，气体摩尔体积、PV=nRT处于把控地位，C组阿伏伽德罗常数、质量、溶液体积处于把控地位。不难发现，物质的量浓度、摩尔质量、气体摩尔体积、阿伏伽德罗常数等均为学生新接触到的物理量，抽象程度高、难理解。这启示我们在教学过程中，如若遇到全新的、陌生的词语，要重点剖析其含义，如“单位物质的量的物质所具有的质量叫做摩尔质量”，质量和摩尔质量之间是什么关系？摩尔质量的计量单位是g还是g/mol？摩尔质量如何取值？摩尔质量受温度、压强等外界因素影响吗？以上问题均需阐明。课本简单的定义描述，以学生的认知发展水平无法挖掘出更多的隐含信息，需重点剖析并辅以对点练习，减少迷思概念的产生。

3.3 块模型

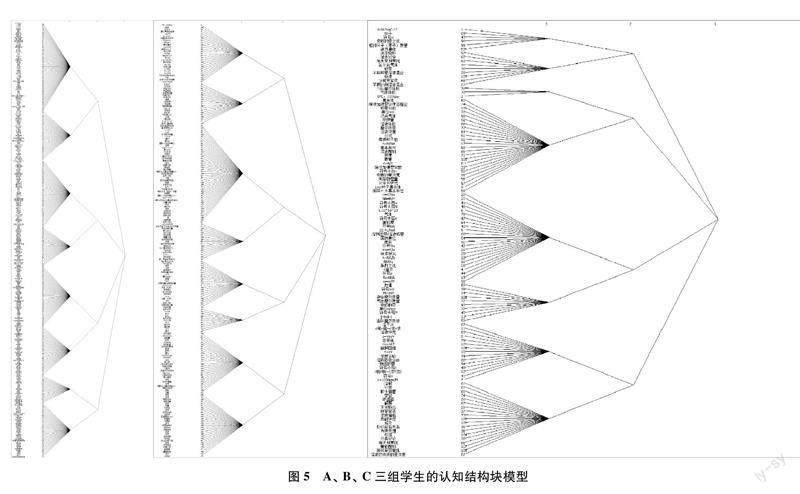
良好的认知结构块模型对知识点的处理和归类方式清晰，有助于高效提取信息；各子块节点密集、关系紧密，有利于信息交流。三组学生的块模型分析结果如图5所示。A、 B组学生的子块分布均匀，知识点归类清晰，具有相似性；C组的子块分布不均，且节点少，其认知结构不完整，知识分类和存储存在障碍。

其中，C组学生的第三子块极小，仅包含三个节点：气体摩尔体积，气体体积，0℃、 101kPa，说明学困生对气体摩尔体积的理解存在缺陷。与前文结果一致。进一步说明，学生需要知识整合和内化的时间，尤其是基础薄弱的学生，在短时间内灌输大量的抽象知识点是极为不可取的教学方式。

4 结论与启示

4.1 结论

本研究采用社会网络分析法对高一年级学生“物质的量”主题认知结构进行探查，得到以下结论：

（1） 由点度中心性可知，气体摩尔体积、物质的量浓度、阿伏伽德罗常数为核心概念。学困生转化可从摩尔质量、气体摩尔体积着手，中等生的提高应关注气体摩尔體积、一定物质的量浓度溶液的配制。对比中间中心性可知，“一定物质的量浓度溶液的配制”是学生认知结构中的重要“桥梁”，是学生突破学习瓶颈的关键。接近中心性研究表明，溶液配制相关知识点对核心概念的依赖程度高。中等生提高需加强证据推理能力，学困生转化应落实基本概念。

（2） 结构洞研究表明，物质的量浓度和摩尔质量处于绝对的控制地位，是展开更深入学习的基础。学生对于物质的量浓度、摩尔质量、气体摩尔体积、阿伏伽德罗常数等物理量的理解存在困难。

（3） 由块模型分析得知，学困生认知结构构建不够完整，出现了极小子块，知识分类和存储时存在障碍，主要体现在对“气体摩尔体积”的理解存在缺陷。

4.2 启示

基于以上研究结论，提出如下教学建议：

4.2.1 抓住关键节点，强化必然联系，实现学困生有效转化

学困生的转化需强化摩尔质量、气体摩尔体积、一定物质的量浓度溶液的配制等知识。中等生的提高应关注气体摩尔体积、一定物质的量浓度溶液的配制、阿伏伽德罗定律。理解摩尔质量和气体摩尔体积的关键在于“摩尔”概念的建立。学生对于摩尔的理解可能仅停留在“摩尔是一个单位”，无法形成清晰的认识。教学中不妨改变概念引入顺序，结合概念起源，按“微粒个数—摩尔—物质的量”的顺序［17］逐一介绍，减少认知负担。此外，气体摩尔体积和阿伏伽德罗定律的教学，也可结合实验探究，先呈现规律，再定量总结。

4.2.2 重视概念生成，体现教学逻辑，促进块模型清晰化

中等生的提高需加强证据推理能力，学困生转化应从基础概念出发，促进构建节点清晰、联系紧密、覆盖全面的认知结构。首先，新授课不仅是讲清楚定义，可结合文字语义、实例类比、化学史料（如摩尔概念的起源、阿伏伽德罗假说的证实过程、NA数值的演变）等多维度阐释基本概念，使抽象的概念通俗易懂。其次，日常教学应注重逻辑链条的完整性，知识生成有理有据，习题讲评重思路讲方法，琐碎知识点结构化呈现，引导学生以“块”为单位存储原本分散的知识点，保证知识提取的高效性。

参考文献：

［1］Ausubel， D. P.. Educational Psychology： A Cognitive View ［M］. New York： Holt， Rinehart and Winston， 1978.

［2］West Fensham P J， Garrard J E L. Describing the cognitive structures of learners following instruction in chemistry ［M］. Orlando： Academic Press， 1985： 29～49.

［3］Stewart， J. Content and Cognitive Structure： Critique of Assessment and Representation Techniques Used by Science Education Researchers ［J］. Science Education， 1979， 63（3）： 395～405.

［4］Qu Zhaohua， Yang Zezhong. The Research on Characteristics of Good Mathematical Cognitive Structure Based on Flow-Map Method-Taking Function as an Example ［P］. Proceedings of the 2017 2nd International Conference on Education， Management Science and Economics （ICEMSE 2017）， 2017： 220～228.

［5］刘军. 整体网分析［M］. 上海： 格致出版社， 2014.

［6］［16］Froehlich， D. E.， Van Waes， S.， Schfer， H. Linking Quantitative and Qualitative Network Approaches： A Review of Mixed Methods Social Network Analysis in Education Research ［J］. Review of Research in Education， 2020， 44（1）：244～268.

［7］Ushakov， K. M.，Kukso， K. N. Advantages of Social Network Analysis in Educational Research ［J］. Russian Education & Society， 2015， 57（10）：871～888.

［8］Sun Dandan， Yang Zehong. Research on the Organizational Characteristics of Good High School Students Mathematical Cognitive Structure Based on the Network Block-Modeling Analysis ［J］. Journal of Educational and Developmental Psychology， 2017， 7（2）：14～23.

［9］張燕清. 基于网络分析的大学生数学认知结构平衡过程研究［D］. 济南： 山东师范大学硕士学位论文， 2020.

［10］洪天慧. 对高中化学教材中“物质的量”内容的编写建议［J］. 化学教学， 2019， （10）： 91～97.

［11］王茜. “物质的量”学习困难成因分析及应对策略［D］. 武汉： 华中师范大学硕士学位论文， 2015.

［12］许嘉铭， 陈新丽， 黄梓键， 周合兵. 国内外“物质的量”主题教学研究现状述评［J］. 化学教育（中英文）， 2022， 43（9）： 112～118.

［13］［14］周青， 闫春更. 学习评价的新方法——流程图法的原理、实施及优势［J］. 当代教师教育， 2016， 9（4）： 12～18.

［15］Wu， Y. T.， Tsai， C. C.  Effects of constructivist-oriented instruction on elementary school students cognitive structures［J］. Journal of Biological Education， 2005， 39（3）： 113～119.

［17］龙琪. “摩尔”概念难点成因及化解策略［J］. 化学教学， 2015， （4）： 32～37.

陕西师范大学2022年度中央高校基本科研业务费专项资金项目“基于学习科学的学生科学课程学业成就评价新技术及优质课程资源的开发研究”（项目编号：GK202204002）阶段性研究成果。