一种可调谐非线性磁式压电能量采集器

丁江 卢蒙恩 曾梓洋 邓爱平 江赛华

（1.广西大学 机械工程学院，广西 南宁 530004；2.华南理工大学 机械与汽车工程学院，广东 广州 510640）

近年来，随着无线传感器等低功耗电子元件的兴起，微小能量的收集得到了广泛关注，尤其是日常生活中振动能量的收集已经成为当前新能源研究领域的热点［1-3］。其中，压电能量采集器具有结构简单、无电磁干扰、响应快速等优点，可以将环境中的振动能转换为电能，是采集振动能量的重要选择，有望替代传统电池为无线传感器、可穿戴电子设备等低功耗产品供电。然而，传统的压电悬臂梁结构仅能在其谐振频率附近有限的带宽内产生较高的功率［4］，当环境振动频率远离采集器的谐振频率时，能量采集效率将显著降低［5-6］。为拓宽采集器的工作频带范围，有效提升振动能量的收集效率，学者们提出了多种改进办法，例如多模态结构、多峰阵列、非线性系统等。其中，通过添加磁铁改变系统刚度可以快速改变系统的非线性特征，实现不同模态下的宽频带能量采集，是当前拓宽采集器共振频带的有效方法之一［7］。

目前，学者们提出了多种非线性磁式压电能量采集器。例如，Stanton等［8］提出了一种非线性磁相互作用可调装置，利用系统的软、硬刚度特性，实现了频率带宽的双向增加；Yang等［9］提出了一种带有磁铁的梁-滑块结构的混合非线性能量采集器，该结构结合了非线性和内部共振机制，与具有固定磁铁的双稳态相比，频率带宽扩大了两倍；Mansour 等［10］提出了一种具有磁性可调节谐振频率的能量采集器结构，利用悬臂梁左端螺钉的轴向移动，改变磁铁的间隙来调整系统的谐振频率，实现系统的谐振频率与外界振源匹配；Ferrari等［11］设计了一种单磁体双稳态压电采集器结构，利用垂直磁铁对单个磁铁悬臂梁产生的吸引力来实现双稳态，改善输出电压；Wang 等［12］建立了非线性三稳态压电能量采集器模型，通过改进的磁偶极子模型准确地计算了非线性磁力、势能和系统的跃迁机理，从而更具体地分析采集器的输出特性；Wu 等［13］在线性双梁结构的基础上，利用永磁铁引入非线性磁力，设计一种多模态结构与非线性结合的能量采集器，使其具有比线性二自由度系统更好的能量采集效果；Firoozy等［14］通过研究一种带有末端磁铁和非线性边界条件的单晶压电采集器结构，给出了一个非线性宽频带压电能量采集器动力学模型的完整推导过程；唐炜等［15］通过系统研究非线性磁式压电结构的建模与分析方法，利用谐波平衡分析法，给出了系统稳态响应的解析表达式；吴义鹏等［16］利用一组带有末端磁铁的非对称压电悬臂梁设计了一种共振频率可调式非线性压电振动能量收集器，可实现在较大频率范围内的频率匹配；杜小振等［17］利用非线性磁力调频设计了一种压电电磁复合发电系统，可采集低频环境下的振动能量。

为了提升调节采集器谐振频率的便捷性，扩大能量收集的共振频带范围，本文通过一对可快速移动的磁铁结构，设计了一种谐振频率可调的非线性磁式压电能量采集器，有效构建了其动力学模型，并通过仿真与实验分析了磁铁间距、阻尼、负载等参数对输出功率和末端磁铁位移的影响，比较了采集器在单、双稳态结构下的性能优劣，拟为可调谐压电能量采集器的设计与分析提供理论指导。

1 压电能量采集器结构

图1所示为压电能量采集器样机结构，其由压电悬臂梁和3个磁铁A、B、C构成。其中，一个磁铁固定在悬臂梁的自由端；两个移动磁铁分别固定在末端磁铁的顶部和底部，呈对称分布。一对压电片对称地粘贴在悬臂梁的上下表面，压电片和悬臂梁长度同为L。末端磁铁沿垂直负方向磁化，两个移动磁铁沿垂直正方向磁化。为了方便调节，压电悬臂梁上下两个挡板固定在可垂直移动的螺栓上，可以通过螺栓便捷地调节移动磁铁和末端磁铁之间的距离，从而改变系统磁斥力大小，实现系统在更宽频率范围内的能量收集。

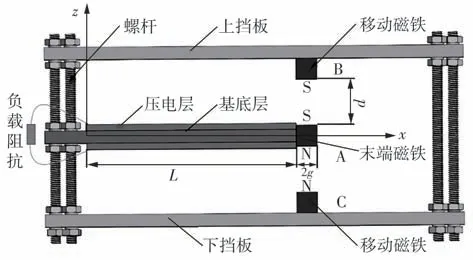
图1 压电能量采集器的结构Fig.1 Structure of piezoelectric energy harvester

2 压电能量采集器动力学模型

如图1所示，以悬臂梁根部的中心位置为原点构建坐标系，水平方向设为x轴，垂直方向设为z轴。基底层和压电层的长度为L，基底层厚度为hb，压电层厚度为hp，末端磁铁的边长为2g，末端磁铁与移动磁铁之间的距离为d，压电层与基底层的宽度分别为wb、wp。系统受到大小为z（t）的谐波激励，沿z方向的位移用w（x，t）表示，忽略其他方向的应变。

2.1 压电悬臂梁的本构方程

根据Euler-Bernoulli 理论，假设压电层和基底层的应变保持一致，只考虑轴向应变，忽略其他方向的应变。记x轴方向为下标1，z轴方向为下标3，系统的应变γ1和电位移D3可以由压电材料的第一类本构方程给出：

式中：σ1为轴向应力；E3为电场强度；d31为压电应变常数；为常应力下的介电常数；为弹性柔顺常数。

2.2 Lagrange函数

利用Euler-Bernoulli 理论建立非线性磁式压电悬臂梁的运动方程。该系统的Lagrange函数可以表示为

式中，T为系统的动能，W为系统的电能，U为系统的势能。系统的动能T包括基底层的动能Tb、压电层的动能Tp和末端磁铁的动能TM。其中，基底层的动能Tb表示为

式中：ρb为基底层密度；Ab为基底层横截面面积；(t)为系统的振动速度；w（x，t）为悬臂梁相对于初始位置的z方向位移。

压电层的动能Tp表示为

式中：ρp为压电层密度；Ap为压电层横截面面积。

末端磁铁的动能TM表示为

式中：Mt为末端磁铁的质量；It为末端磁铁的转动惯量。

在本研究中，两个压电片对称粘贴在梁的上下表面，极化方向相反，因此机电耦合系数符号相反。系统的输出端采用串联连接，假定每个压电片的电场强度在z方向上均匀分布。因此系统的电能为压电片的电能Wp，可以表示为

式中：v（t）为压电片的电压；e31为压电片的机电耦合系数；Cp=b/hp。系统的势能U包括基底层的势能Ub、压电层的势能Up和磁铁间的排斥力产生的势能UAB、UAC。基底的弹性势能Ub表示为

式中：Yb为基底层的弹性模量；Ib为基底层的截面惯性矩，其中Ib=wb/12。

压电片的弹性势能Up表示为

式中，Ip为压电片的截面惯性矩，

磁场势能UAB、UAC的计算涉及到磁力的分析，是本文研究的重点，将在下节叙述其分析过程。

2.3 磁力分析

如图2所示，根据磁铁之间的几何关系，本文通过偶极子模型描述非线性磁力。

图2 磁场势能分析Fig.2 Magnetic potential energy analysis

考虑双磁铁来推导出垂直或平行于磁偶极子的分离矢量，引入mA、mB和mC来分别表示磁铁A、B 和C 的磁矩矢量。磁矩矢量的取向如图2 所示，可以写成：

式中，M为磁化强度，代表磁铁材料内所有微观磁矩的矢量和，V为磁铁的体积。

使用rAB、rAC表示磁铁B、C 到磁铁A 的距离，e1、e2表示x、y方向的单位矢量。由于g≪L，则α约等于0°，末端磁铁和移动磁铁之间的距离关系可表示为

磁铁A、B、C的磁矩可以表示为

磁铁A 在磁铁B、C 处产生的磁通密度BBA、BCA可表示为

式中：‖ · ‖2为欧几里得2 范数；∇为矢量梯度算子；μ0为真空磁导率。

磁铁间的势能UAB、UAC可以表示为

由偏转角α和挠度w（l，t）的关系可得：

由于g≪L，α≈0°，则sinαcosα≈0、sin2α≈0、sin3α≈0。联立式（11）-（15），势能UAB、UAC可以表示为

式中，q为与时间相关的广义模态坐标，系数分别为

其中φ（·）为悬臂梁的特征函数。

2.4 Lagrange函数的空间离散化

为了得到Lagrange 函数的降阶模型，采用Galerkin离散方法，梁的横向位移近似为［18-19］

式中，ϕi(x)为悬臂梁的第i个特征函数，qi（t）为与时间相关的广义模态坐标。

根据Friswell 等［20］的研究，可以由一阶模态来获取系统的降阶方程，通过考虑单模近似，式（17）可以简化为

式中，ϕ1(x)可以通过求解带有末端磁铁的无阻尼线性悬臂梁的特征值问题获得，其中一阶模态可以表示为［21］

其中，k'为常数项系数，

λ为一阶模态的特征值，mp、mb分别为压电片、悬臂梁质量。

通过在x=0 和x=L处的边界条件来确定振型中的系数：

式中，YI为悬臂梁的整体抗弯刚度，根据梁的模态频率关系可得

式中，m为悬臂梁的质量。

将式（19）代入式（20）中，结合式（21）可得到A1η1=0 的等式，其中A1为2×2 的系数矩阵，η1=|AC|T。为得到系统的非平凡解，需要令系数矩阵的模为零，据此计算出多阶模态频率ωi，并根据ωi计算特征向量d，从而求出各阶模态振型系数。

为保证各阶振型的唯一性，模态振型函数还应满足下列正交条件：

式中，当r=h时，δrh=1，当r≠h时，δrh=0。

2.5 机电耦合动力学方程

为了表示压电采集器连接电路后的耦合行为，接下来推导压电振子的输出电压v（t）的表达式，电路如图3所示。

图3 压电能量采集器等效电路模型Fig.3 Equivalent circuit model of piezoelectric energy harvester

根据式（1）可得［22］：

压电悬臂梁中的电荷可表示为

式中，Yp为压电层的弹性模量，hpc为压电片到中性轴的距离。

根据电荷和电流的关系可得：

连接电路后，根据电压-电流方程，可以得到电压表达式：

将式（18）代入式（16），并进行泰勒展开得：

将式（18）代入式（3）、（4）、（5）可得动能表达式：

将式（18）代入式（9）得：

将式（18）代入式（7）、（8）、（28）得势能表达式：

为了获得动力学方程的一阶模态近似函数，Lagrange函数可以表示为

将式（28）-（30）代入式（31），并考虑粘性阻尼系数cv的影响，采集器的非线性运动方程以广义坐标的形式可表示为

其中，K1=2N1+2N3+2N5，K2=2(N7+N8-3s2)，K3=-9s3，K4=4s4，K5=N9+θ1，K6=2(N2+N4+N6)，K7=s1。

令K2/K1=s，K4/K1=k，式（32）已化简成达芬尼方程的形式。由式（30）、（32）可知，磁势能导致非线性刚度k的出现，同时改变了线性刚度s的大小，因此磁势能是造成能量采集器系统非线性的根源。由式（27）可以看出，磁性势能由磁铁强度、磁铁体积、梁的模态振型和磁铁间距等参数决定。其中，磁铁间距d因便于调整，可以被用来调节采集器的谐振频率。

2.6 谐波平衡法求解

为了便于分析系统的各种因素对输出的影响，本文利用谐波平衡法求系统的解析表达式，假设基座加速度为=a0cos(ωt)，ω为外激励频率，式（26）、（32）中机电耦合方程的稳态解可以表示为

式中，a2表示系统的平衡位置。

令式（33）中的sin项、cos项和常数项的系数相同可得：

式中，η0为系统的位移幅值。

根据式（34），可得到稳态情况下系统的平均输出功率：

3 采集器的仿真分析

为了验证可调谐非线性磁式压电能量采集器的性能，本节将依据式（35）-（37），针对采集器的单、双稳态快速切换和输出等问题进行研究，采用的物理参数如表1所示。

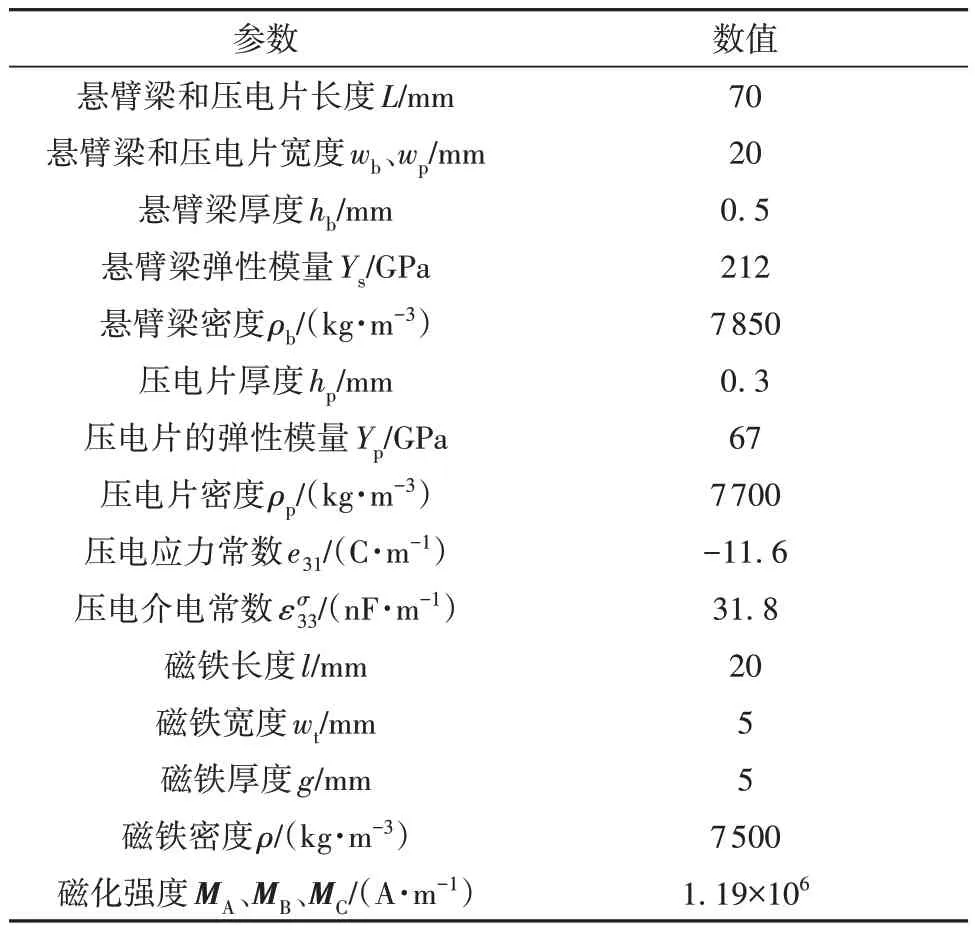
表1 采集器的材料和结构参数Table 1 Material and structural parameters of harvester

磁力大小是影响压电能量采集器非线性的主要因素，通过改变磁铁间距d的大小，可以调整采集器非线性行为的强弱。为量化这种影响，利用表1数据，通过仿真分析给出了采集器线性刚度和非线性刚度随d变化的曲线，如图4 所示。当d=d0=17.8 mm 时，线性刚度为零，因此d0为临界点，当d＜d0时，s＜0，k＞0，系统表现为双稳态特性；当d＞d0时，k＞0，s＞0，系统表现为单稳态渐硬特性。

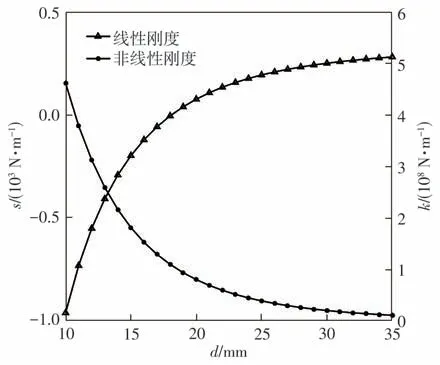
图4 能量采集器线性刚度、非线性刚度随磁铁间距的变化Fig.4 Change of linear stiffness and nonlinear stiffness of energy harvester with magnet spacing

3.1 双稳态特性

由图4可知，当d＜17.8 mm时，系统表现为双稳态特性。为分析系统的双稳态特性，本文讨论加速度幅值、频率、磁铁间距和负载阻抗等参数对系统响应和输出的影响。首先分析了采集器末端磁铁的幅频响应曲线，如图5所示。假设负载RL=1 000 kΩ，阻尼为0.1，对比磁铁间距d分别为10、15 mm 以及激励加速度a分别为1、2 m/s2情况下的幅频响应曲线。图5中的幅频响应曲线中包括小幅阱内运动和大幅阱间运动，当η0＜3.5 mm 时，属于小幅阱内运动，当η0＞3.5 mm 时，属于大幅阱间运动。由图5 可知，小幅阱内运动的幅频响应曲线向左倾倒，与单稳态软特性的幅频响应曲线类似；大幅阱间运动的幅值随外激励频率的增大而增大，在低频附近也会有较大的幅值响应，适用于低频环境下的振动能量采集。对比图5（a）和5（b）或对比图5（c）和5（d）可知，加速度幅值增加将明显扩大阱间运动频带范围，略微增加小幅阱内运动频带范围；对比图5（a）和5（c）或对比图5（b）和5（d）可知，磁铁间距d对大幅阱间运动幅值和频带的影响并不显著，对小幅阱内运动的频带影响较为明显，随着d的增大，阱内运动的频带右移。

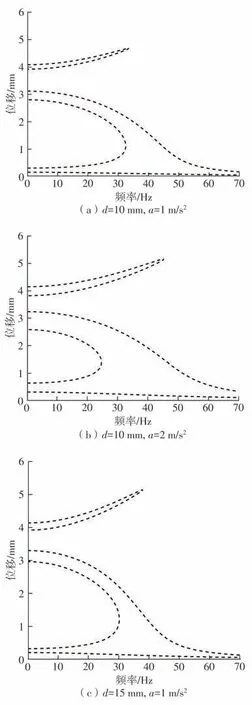
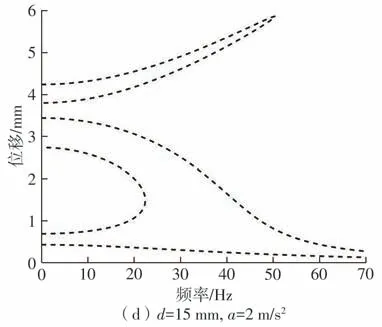
图5 采集器的幅频响应曲线Fig.5 Amplitude-frequency response curve of harvester

为了分析负载阻抗对系统输出功率的影响，图6 给出了d=15 mm 时，系统处于双稳态阱间运动时输出功率随负载的变化。其中，图6（a）对比ω分别为35、40、45 和50 Hz 4 种不同激励频率下，输出功率与负载的关系。可以看出，每种激励频率都存在各自的最优阻值，在此阻值下系统将获得最大输出功率，且最大输出功率随激励频率的增加而增加，但最优阻值随激励频率的增加而降低。图6（b）对比a分别为0.5、1.0、1.5和2.0 m/s24 种不同激励加速度下，输出功率与负载的关系。可以看出，最大输出功率随加速度幅值的增加而增加，但是最优阻值并不随加速度幅值改变而发生显著变化，始终保持在830 kΩ附近。

图6 d=15 mm时阱间负载阻抗-输出功率关系曲线Fig.6 Relationship curve between load impedance and output power between wells when d=15 mm

为分析负载对系统输出功率的影响，图7给出了d=15 mm时，系统处于双稳态阱内运动时输出功率随负载变化的曲线。其中，图7（a）对比了ω分别为35、40、45和50 Hz 4种不同激励频率下，输出功率与负载的关系。可以看出，每种激励频率都存在最优阻值，在此阻值下系统将获得最大输出功率，且最大输出功率随激励频率的增加而降低，同时最优阻值随激励频率的增加而减少。图7（b）对比a分别为0.5、1.0、1.5和2.0 m/s24种不同激励加速度下，输出功率与负载的关系。可以看出，最大输出功率随加速度幅值的增加而增加，但是最优阻值并不随激励大小发生显著变化，始终保持在620 kΩ附近。

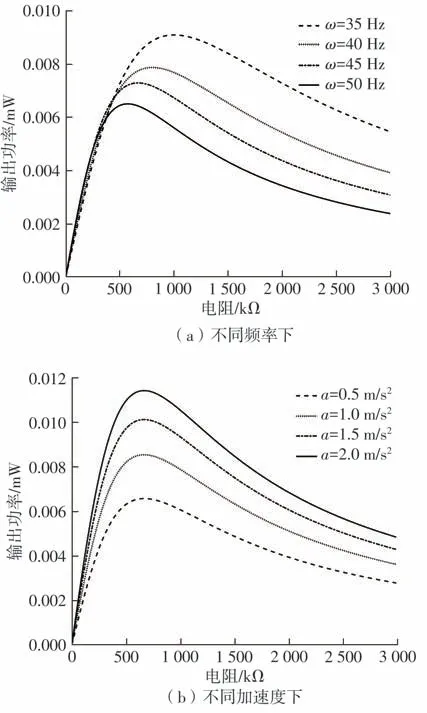
图7 d=15 mm时阱内负载阻抗-输出功率关系曲线Fig.7 Relationship curve between in well load impedance and output power when d=15 mm

3.2 单稳态特性

由图4 可知，当d＞17.8 mm 时，系统表现为单稳态渐硬特性。图8给出了系统处于单稳态时输出功率随负载变化的关系，对比了不同磁铁间距d和末端磁铁质量Mt对输出功率的影响。假设外激励加速度a=2 m/s2，阻尼为0.1，对比磁铁间距d分别为20、25 mm以及末端磁铁质量Mt分别为7、14 g情况下的频率响应曲线。由图8（a）可知，对于质量相同的末端磁铁，通过增加磁铁间距，系统的最优阻值向右移动，输出功率增加；由图8（b）可知，对于相同的磁铁间距，通过增加末端磁铁的质量，最优阻值向右移动，输出功率增加。

图8 系统处于单稳态时负载阻抗-输出功率关系曲线Fig.8 Relationship curve between load impedance and output power when the system is in monostable state

图9给出了系统处于单稳态时末端位移随频率变化的关系，并对比了不同末端磁铁质量Mt和磁铁间距d对位移的影响。假设外激励加速度a=2 m/s2，阻尼为0.1，对比磁铁间距d分别为20、25 mm 以及末端磁铁质量Mt分别为7、14 g 情况下的幅频响应曲线。由图9（a）可知，在末端磁铁质量不变的情况下，随着磁铁间距的增加，采集器的最大位移幅值降低，有效频带范围减小，同时系统的非线性行为降低。由图9（b）可知，在磁铁间距不变的情况下，随着末端磁铁质量的增加，采集器的末端位移幅值随之增加，同时系统的谐振频率向左移动，可以采集低频下的能量，但系统的有效工作频带范围不会发生明显改变。

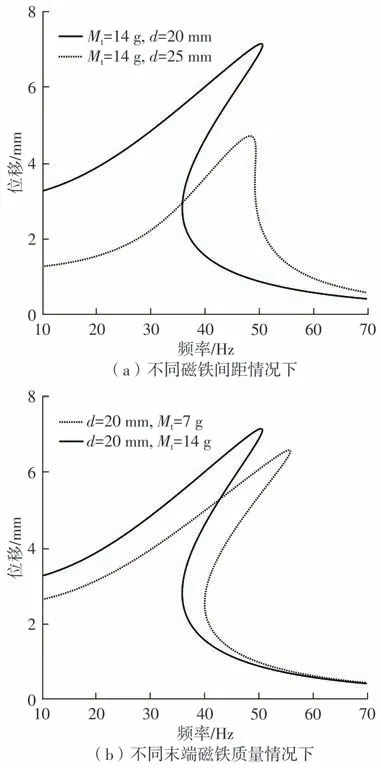
图9 系统处于单稳态时采集器的幅频响应曲线Fig.9 Amplitude-frequency response curve of harvester when the system is in monostable state

如图10 所示，取阻尼为0.1，磁铁间距d=20 mm，负载RL=400 kΩ，末端磁铁质量Mt=7 g，研究在加速度a为1、2 和3 m/s23 种不同情况下，位移和输出电压随频率的变化。从图10 可以看出，采集器在a为1、2 和3 m/s23 种不同激励水平下的最大位移幅值分别为4.96、6.59和7.26 mm，最大输出电压分别为2.78、4.73 和5.91 V。可以看出，随着加速度幅值的增加，末端磁铁的位移幅值和系统的输出电压随之增加，且最优谐振频率向右移动。

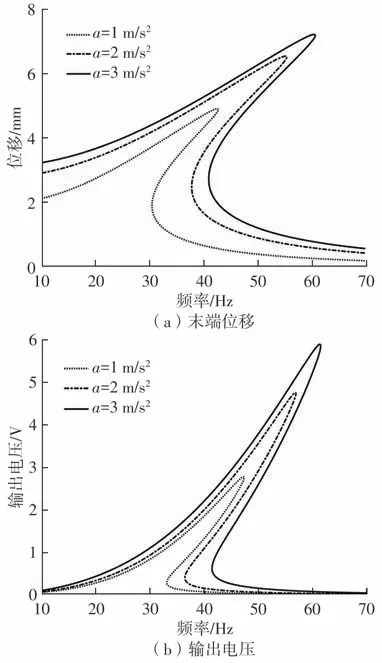
图10 不同加速度对系统末端位移和输出电压的影响Fig.10 Influence of different accelerations on end displacement and output voltage

如图11 所示，取加速度a=2 m/s2，d=20 mm，R=400 kΩ，Mt=7 g，研究阻尼ε=0.025，0.05，0.1 3 种不同情况下，系统末端位移和输出电压随频率变化的响应。由图11可知，采集器在3种阻尼下的最大位移幅值分别为8.31、7.16和6.96 mm，最大输出电压分别为7.20、5.31 和4.73 V。可以看出，通过增加机械阻尼，系统的非线性行为开始降低，并且最大位移幅值和最大输出电压都在下降，最优谐振频率向左移动；通过增加机械阻尼，系统的非线性硬化特性逐渐减弱。

图11 不同阻尼对末端位移和输出电压的影响Fig.11 Effect of different damping on end displacement and output voltage

为分析有无末端磁铁对系统位移和输出电压的影响，取加速度a=2 m/s2，阻尼ε=0.1，磁铁间距d=20 mm，负载RL=400 kΩ，研究了系统在不存在末端磁铁和末端磁铁质量Mt=7 g 情况下的输出响应。如图12所示，在不存在末端磁铁的情况下，系统的最大位移幅值为5.18 mm，最大输出电压为3.07 V；在末端磁铁Mt=7 g的情况下，系统的最大位移幅值为6.59 mm，最大输出电压为4.73 V。可以看出，磁铁的存在增加了系统的输出，改变了系统的有效工作频带范围，系统的最优谐振频率右移，同时增加了系统的非线性行为，系统的非线性硬化特性明显。

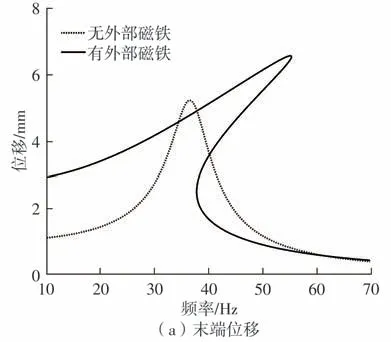
图12 有无磁铁对末端位移和输出电压的影响Fig.12 Effect of presence or absence of magnet on end displacement and output voltage

为分析负载阻抗对系统输出功率的影响，图13研究了d=20 mm时，系统单稳态输出功率随负载变化的曲线关系。图13（a）对比了ω=40，45，50，55 Hz 4 种不同激励频率下，功率随负载变化的曲线。可以看出，每种激励频率都存在各自的最优阻值，在此阻值下系统将获得最大输出功率，且最大输出功率随激励频率的增加而增加，但最优阻值随激励频率的增加而减少。图13（b）对比了a=0.5，1.0，1.5，2.0 m/s24 种不同激励加速度下，功率随负载变化的曲线。可以看出，最大输出功率随加速度的增加而增加，但是最优阻值并不随加速度变化而发生显著变化，始终保持在400 kΩ附近。

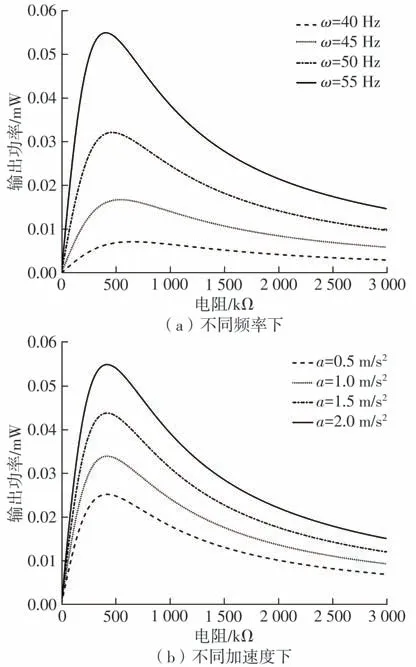
图13 d=20 mm时负载阻抗-系统单稳态输出功率关系曲线Fig.13 Relationship curve between load impedance and output power of the system in monostable state when d=20 mm

4 实验分析

为了验证提出的可调谐非线性磁式压电能量采集器的发电性能，通过实验测试验证仿真分析与理论分析的正确性，实验平台如图14 所示。实验测试系统主要的硬件设施包括Tektronix AFG2021 函数信号发生器、世傲SA-PA010 功率放大器、世傲SA-JZ002 模态激振器、澄科NI 多功能USB-6002 DAQ 数据采集卡、世敖加速度传感器、世敖CT5204 恒流适配器以及计算机等设备。实验原理为：函数信号发生器产生正弦激励信号，经过功率放大器传给模态激振器产生振动，然后作用于可调谐非线性磁式压电能量采集装置上，加速度信号经过恒流适配器传给示波器，利用示波器分析加速度传感器输送的信号。非线性磁式压电能量采集装置将振动能量转换为电能，同时外接一个纯电阻，通过数据采集卡收集负载电阻上的电压信号，并由计算机进行分析。

图14 实验测试平台Fig.14 Experimental test platform

4.1 磁铁间距及外部磁铁对系统特性的影响

为研究采集器谐振频率与磁铁间距的关系，记录了不同磁铁间距下的谐振频率，测试结果如图15所示。结果显示通过调节磁铁间距可以使采集器在36～55 Hz范围内拥有有效的共振频带。在0～20 mm内，当磁铁间距逐渐增加时，磁斥力可以增加系统刚度，采集器的谐振频率逐渐增加，并在磁铁间距为20 mm 时达到最大调节值；在20～30 mm 内，当磁铁间距逐渐增加时，由于磁斥力减弱，系统刚度逐渐降低，采集器的谐振频率从55 Hz 逐渐减小。

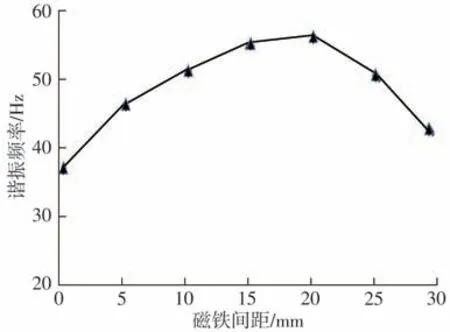
图15 磁铁间距与采集器谐振频率的关系Fig.15 Relationship between magnetic distance and resonant frequency of harvester

为研究末端磁铁对采集器输出性能的影响，分别记录了存在、不存在末端磁铁情况下采集器的电压值。其中，取加速度a=2 m/s2，磁铁间距d=20 mm，负载R=400 kΩ，调整信号发生器使其输出频率为10～70 Hz，测试结果如图16 所示。在没有外部磁铁的情况下，采集器为一个经典线性压电悬臂梁系统，系统的最大输出电压为3.13 V，此时的频率为35 Hz；在有外部磁铁的情况下，压电发电系统表现出非线性硬化现象，最大输出电压为4.74 V，此时频率为55 Hz，随后产生跳跃现象。而仿真分析的结果表明，系统的最大输出电压为3.07、4.73 V，此时频率为36.64、55.36 Hz。可见，在实验误差允许范围内，实验结果与仿真结果分析一致。当外激励频率超过55 Hz 后，采集器的幅频响应曲线产生跳跃现象。这是因为幅值响应较小，压电片变形较小，导致产生的电压较低。

图16 外部磁铁对采集器输出电压的影响Fig.16 Influence of external magnet on output voltage of harvester

4.2 双稳态性能测试

为测试采集器在双稳态阱间下的输出性能，验证了不同加速度下采集器的功率响应。调整挡板以维持磁铁间距d=15 mm，调整信号发生器使其输出频率为50 Hz、振幅分别为1和2 m/s2的正弦波信号，测得不同加速度幅值下负载电阻功率与负载电阻值的关系，如图17 所示。从图17 可以看出，增加外激励加速度可以提升采集器的输出功率，在外激励加速度分别为1 和2 m/s2时，采集器的最大输出功率分别为0.035和0.055 mW，此时的负载电阻值约为800 kΩ。而仿真分析的结果表明，系统的最大输出功率分别为0.035、0.056 mW，此时的负载电阻值约为830 kΩ。从上述数据可以看出，改变外激励强度不影响采集器的最优阻值，且在实验误差允许范围内，实验结果与仿真分析结果一致。

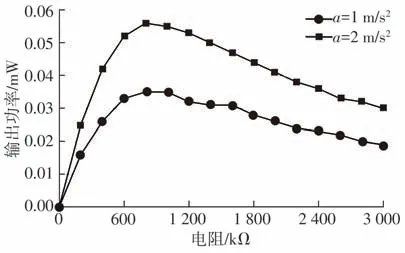
图17 双稳态阱间下不同加速度时输出功率与负载电阻值的关系Fig.17 Relationship between output power and load resistance value under different accelerations between bistable wells

为测试采集器在双稳态阱间下的输出性能，验证了不同激励频率下的功率响应。调整挡板以维持磁铁间距d=15 mm，调整信号发生器使其输出频率为40和50 Hz、振幅为2 m/s2的正弦波信号，测得不同激励频率下负载电阻功率与负载电阻值的关系，如图18所示。

图18 双稳态阱间下不同激励频率时输出功率与负载电阻值的关系Fig.18 Relationship between output power and load resistance value under different excitation frequencies between bistable wells

4.3 单稳态性能测试

为测试采集器在单稳态下的输出性能，验证了不同加速度下采集器的电压响应。调整挡板以维持磁铁间距d=20 mm，将外部负载电阻值选为400 kΩ，调整信号发生器使其输出频率为10～70 Hz、振幅分别为1、2和3 m/s2的正弦波信号，通过数据采集卡采集负载电阻的电压，结果如图19 所示。从图19 可以看出，随着外激励加速度的增加，采集器的输出电压逐渐增加。在外激励加速度分别为1、2 和3 m/s2时，采集器的最大输出电压分别为2.6、4.5和5.9 V，此时的激励频率分别为46、56 和62 Hz。从实验结果可以看出，增加外激励加速度可以提升采集器的输出性能，且系统的谐振频率全部位于线性谐振频率的右侧。而仿真分析的结果表明，在此条件下系统的最大输出电压分别为2.78、4.73、5.91 V，此时频率为47.16、55.36、60.64 Hz。由此可见，在实验误差允许范围内，实验结果与仿真分析结果一致。

图19 单稳态下负载电阻电压与外激励加速度的关系Fig.19 Relationship between load resistance voltage and external excitation acceleration under monostable state

为测试采集器在单稳态下的输出性能，验证了不同加速度下采集器的功率响应。调整挡板以维持磁铁间距d=20 mm，调整信号发生器使其输出频率为55 Hz、振幅分别为1 和2 m/s2的正弦波信号，测得不同外激励加速度下负载电阻功率与负载电阻值的关系如图20 所示。从图20 可以看出，增加外激励加速度可以增加采集器的输出功率，在外激励加速度分别为1 和2 m/s2时，采集器的最大输出功率分别为0.035和0.054 mW，此时的负载电阻值约为400 kΩ。从上述数据可以看出，改变外激励加速度不影响采集器的最优阻值。而仿真分析的结果表明，在此条件下系统的最大输出功率分别为0.034、0.055 mW，此时的负载电阻值为400 kΩ。可见，在实验误差允许范围内，实验结果与仿真分析结果一致。

图20 单稳态下不同加速度时输出功率与负载电阻值的关系Fig.20 Relationship between output power and load resistance value under different accelerations in monostable state

为测试采集器在单稳态下的输出性能，验证了采集器的电压、功率响应。调整挡板以维持磁铁间距d=20 mm，调整信号发生器使其输出频率为55 Hz、振幅为2 m/s2的固定正弦波信号，测得负载电阻功率、电压与负载电阻值的关系如图21 所示。从图21可以看出，实验结果显示采集器的输出功率随着负载电阻值的增加呈现先增加后减小的趋势，在400 kΩ附近达到最大值，此时输出功率为0.054 mW，电压值为4.6 V；电压首先随着负载电阻值的增加而增加，当负载电阻值超过最优阻值后，电压增加缓慢，随后趋于平缓。

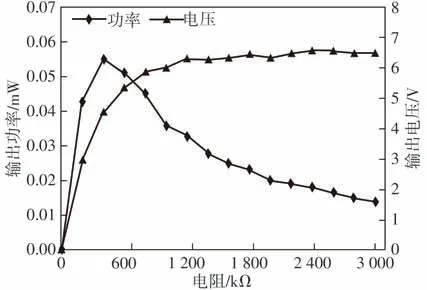
图21 单稳态下采集器输出功率、电压与负载电阻的关系Fig.21 Relationship between output power，voltage，and load resistance of harvester in monostable state

5 结论

本文设计了一种可调谐非线性磁式压电能量采集器结构，对采集器进行分布参数动力学分析，建立了系统动力学方程，利用谐波平衡法得到方程的解析表达式，并通过仿真分析与实验得到以下结论：

（1）通过改变磁铁间距，可改变系统的谐振频率，并可使系统进行单、双稳态的转换，当d＜17.8 mm 时，系统表现出双稳态特性，可以采集低频环境下的振动能量；当d＞17.8 mm时，系统表现出单稳态渐硬特性，可以采集高频环境下的振动能量。

（2）系统的最优阻值受到悬臂梁末端磁铁质量、磁铁间距和外激励频率的影响。其中，随着末端磁铁质量的增加，系统的最优阻值也随之增加；随着磁铁间距的增加，系统的最优阻值随之增加；对于单、双稳态，系统的最优阻值都是随着外激励频率的增加而减小；外激励加速度的大小对于系统的最优阻值影响较小。

（3）对于单稳态系统，通过增加磁铁间距，会降低系统的非线性行为，减小系统的位移响应幅值，同时减小有效工作频带范围；通过增加末端磁铁质量，可以增加系统的位移响应幅值，并降低系统的谐振频率，可用于采集低频环境下的能量。

（4）改变系统的阻尼和外激励加速度会对系统的输出产生影响。其中，通过减小阻尼系数可以增加系统的位移幅值及输出电压，非线性行为也更加明显；通过增加外激励加速度会增加系统的位移幅值及输出电压，并提升系统的最优谐振频率，可用于采集高频环境下的能量。