基于时空双细胞状态的轴承剩余使用寿命预测方法
李方 郭炜森 张平 罗龙
(华南理工大学 计算机科学与工程学院,广东 广州 510006)
故障预测和健康管理(PHM)是指利用大量状态监测数据和信息,借助统计算法或模型来评估和管理装备的健康状态,提前对潜在故障进行预测。剩余使用寿命(RUL)预测技术是PHM 的关键技术之一,其通过分析传感器监测的运行数据或建立合适的退化模型对系统或部件的RUL进行提前预测,提高生产过程的安全性及降低维护成本。
目前,实现轴承剩余使用寿命预测的主流方法大致可以分为:基于物理模型的预测方法[1]和基于数据驱动的预测方法[2],以及上述两种方法的混合方法[3]。基于物理模型的方法一般需要行业专家的知识来对目标系统内部运行机制进行建模分析,构建物理模型描述衰减过程,优点是对于特定系统准确性有保证。然而,轴承的寿命衰减过程复杂,不同环境对应不同的衰减模式,以至于难以实时地使用物理模型对其系统状态进行描述[3]。随着人工智能、大数据等技术的蓬勃发展,加上物联网、传感器和信号处理技术的普及,基于数据驱动的方法逐渐成为主流[4],而在数据驱动方法中,基于深度学习的方法是近年来的代表[5],其通过借助一些机器学习算法和深度学习算法,如支持向量机(SVM)[6]、相关向量机(RVM)[7]、人工神经网络(ANN)[8]、卷积神经网络(CNN)[9-10]、递归神经网络(RNN)[11]、长短时记忆网络(LSTM)[12]等建立有效的RUL 预测模型,对监测数据进行处理以实现RUL预测。因其不依赖专家经验以及所研究系统的内部机制知识,且性能强大,所以能够自适应地从原始数据中学习到特征,从而能准确地对寿命衰减过程进行建模[5]。
卷积神经网络有着强大的特征提取能力,广泛应用于图像、语音识别等领域,也可应用于RUL的预测。Li等[13]基于时频域特征提取方法,对原始数据进行短时傅里叶变换,进而采用多尺度卷积神经网络对其进行进一步特征提取,具体为每段采样样本进行多卷积层输出的拼接,然后将连续采样段经过多尺度提取后的特征按元素相加,并将获得的高层特征映射为RUL;Zhu 等[9]提出一种基于时频域体征提取的多尺度卷积神经网络MSCNN,采用小波变换将原始数据转化为二维图像,然后输入到卷积神经网络,经过多层卷积和池化操作后,将最后两层特征图通过拼接方式组成最终特征,通过全连接网络输出得到RUL 预测值。Wang 等[14]提出了一种基于3D 卷积的RUL 预测方法,首先将原始信号以连续小波变换转化为2维图,再以时间维度堆叠成3 维张量,最后输入到3D 卷积神经网络中提取特征,并预测得到健康指标(HI),之后利用已得到的HI 由高斯过程回归的方法估计得到未来的健康指标。
由于循环神经网络及其变体有着强大的时序建模能力,所以非常适合剩余使用寿命预测任务,是长久以来的研究热点。Guo 等[11]提出了一种方法,其采用手工提取时域、频域、时频域特征,然后从中筛选出单调性和趋势性平均最好的特征,进而将其作为循环神经网络的输入,最后输出设备的健康指标。对于未来的HI,根据当前HI 曲线采用双指数模型进行拟合,得到完整的HI 曲线,并设计一个阈值,当HI 超过该阈值时则判定设备为失效。Ma 等[15]采用连续小波变换将原始信号转为二维矩阵,然后将该矩阵按列划分为时间上连续的列向量,作为门控循环网络(GRU)的输入预测RUL;Chen 等[16]采用了一种编码器-解码器结构的双向GRU 网络,在PHM2012 数据集中,将原始数据的频域谱分为5个子频带作为模型输入,在编码器的输出中加入了注意力机制,解码器经过注意力权重计算得到预测结果;温海茹等[17]提出了一种深度学习混合的DCNN-LSTM 网络系统模型,将深度卷积神经网络作为特征提取网络、堆叠的LSTM 作为时序特征提取器,并利用网格搜索算法得到最优混合模型超参数,最后在C-MAPSS 数据集上实验,得到了较好的结果。Qin 等[18]提出了一种基于双门阀注意力的门控循环单元网络,该网络通过对输入和隐状态做一种自注意力和对重置门与更新门的注意力,来提升网络对状态转移中的关键信息捕捉能力,增强RUL 的预测能力。Xiang 等[19]提出了一种时空多差分处理的RUL预测方法,该方法修改细胞状态,以内部自差分的方法得到多种不同的记忆体,分别有长期、长中期、中期、中短期、短期状态记忆,并将原有的全局和局部趋势再细分为对应趋势,他们认为这样的差分能够充分反映设备长期和短期衰减趋势;另外,该方法还通过循环和卷积网络双路预测分别提取传感数据空间和时间上的特征,并预测所处阶段,再根据对应衰减阶段进行相应的特征提取处理。
但是,将浅层特征提取器和循环神经网络进行串联结合无法最大地发挥两者的优势。Wang 等[20]提出了一种基于卷积操作的门控循环单元神经网络,该网络本质上是一种结合了卷积操作的循环神经网络。该方法采用不依赖手工数据特征工程,直接将原始数据作为模型输入,实现了真正端到端的学习。经过多层卷积GRU 网络后以一种蒙特卡洛丢弃的不确定性方法来预测RUL,使模型预测的不确定性降低。Ma等[3]对原始轴承振动数据采用短时傅里叶变换方法转换为二维图像,然后输入到带有卷积操作的长短期记忆单元网络提取深层特征,进而预测RUL;Lei 等[21]提出了一种带有残差链接块的卷积长短期记忆网络,其在每层的输入端加深了对输入的特征提取,并为了保证梯度更好地传播而在此加入了残差链接;另外,该文献还提出了一种相比蒙特卡洛丢弃方法更有效率的不确定性RUL预测方法,其通过设计一定的损失函数和两个子网络分别预测结果的方差和均值来达到快速的不确定性预测;Li等[22]采用基于一种自注意力的卷积长短期记忆网络的方法来预测设备剩余使用寿命。该方法提取原始信号的24 个时域和频域特征,根据单调性和趋势性进行筛选,并将筛选后的特征输入到自动编码器进行特征提取和降维,最后将其输入到带有自注意力机制的卷积长短期记忆网络中,给定若干样本点预测设备后续的健康指标。
然而,在实际生产的RUL 预测中,如何使用数据驱动的方法准确预测轴承等设备部件的寿命,仍然面临很多挑战。首先,在不同环境下,轴承的寿命衰减行为不尽相同,即使在同一环境下,由于部件出厂状态在统计上存在方差,个体之间的初始差异导致衰减过程存在不同,因此,设备寿命受环境影响深刻;其次,在剩余使用寿命预测任务中,不同采样段中采集的数据存在时间相关性,即除了单段连续采样的数据存在时序关系之外,时间上存在先后顺序的不同采样段之间的数据同样存在一定的时间相关性,例如不同衰减状态的数据有前后发生关系。卷积神经网络因其强大的特征提取能力[23]以及对噪声不敏感而被广泛用于图像、语音识别等应用中[24]。循环神经网络则因优秀的时序依赖信息建模能力被应用于自然语言处理任务中[25]。近年来,将上述两者进行结合的方法逐渐应用于轴承的剩余使用寿命预测[3],除简单进行拼接的网络结构之外[12],将两种网络原生地进行融合,例如卷积长短期记忆网络(CLSTM)[26]在原有的时序建模体制中引入了卷积操作,考虑到了空间特征的提取。但是,现有的方法仍没能实现时序和空间特征的深层结合,因此,在引入卷积后不同层之间空间信息利用效率的低下,致使不能有效地捕捉轴承在衰减过程中的时空信息,造成信息损失,进而无法得到准确的剩余使用寿命预测结果。
针对以上挑战,本文提出一种基于时空双细胞状态自适应网络(ST-DCSN)的轴承剩余使用寿命预测方法:采用一种时间状态和空间状态并存的内嵌卷积操作双状态循环网络,同时引入水平方向传播的时间状态和垂直方向传播的空间状态;提出双细胞机制,通过静态和动态子细胞状态,有效准确地对带有时空特征的原始信号进行特征提取;采用时空双细胞状态和子细胞状态差分机制,实现对轴承衰减状态的自适应感知。该方法拟在时间和空间维度上对设备监测数据进行特征状态的有效捕捉,解决剩余使用寿命预测中环境和时序问题对预测性能的影响。
1 时空双细胞机制网络结构
1.1 卷积长短期记忆网络
卷积长短期记忆网络(CLSTM)如图1 所示,最早在2015 年被提出[26],其衍生方法卷积门控循环单元(CGRU)在2019年被使用在剩余使用寿命预测任务上[20],此后亦被使用于提取2D 频谱图像中的衰减特征来预测轴承的剩余使用寿命[3]。它通过在循环神经网络中内嵌卷积操作,于原有的长短期记忆单元中将状态转移计算从按元素乘法操作替换成卷积操作,并且在层之间加入了池化层,能自动地对输入信号进行空间维度上的特征提取。该网络不仅有长短期记忆网络的长期依赖建模能力,而且在加入卷积操作后能够进行输入中的深度空间信息提取,原生地支持时空复合信息的提取。其中,时刻t的隐藏状态输出ht的计算过程为

图1 卷积长短期记忆网络[26]Fig.1 Convolutional long-short term memory network[26]
式中:“*”代表卷积运算;“⊙”表示哈达玛积;“[]”表示张量拼接操作;σ和δ分别表示sigmoid和tanh激活函数;ft表示遗忘门,it表示输入门;ot表示输出门;x为当前细胞体的输入数据;ht-1为上一时刻细胞体隐藏状态输出;为当前候选状态;ct为当前细胞体状态;Wf、Wi、Wo、Wc分别表示对应计算中各自独立可训练的权值参数;bf、bi、bo、bc表示对应计算中各自独立可训练的偏置参数。
1.2 时空双细胞状态网络结构
Wang 等[27]在图像处理和视频预测领域提出了时空-长短期记忆细胞的结构,本文在Wang等[20]和Ma等[3]对于轴承剩余使用寿命预测研究基础上提出了ST-DCSN 网络结构,如图2所示。该网络基于一维卷积并引入了全局池化层,将由深层堆叠的时空卷积长短期记忆网络提取的深层特征经最后一层全局池化后,得到RUL特征。另外,本文还创新地引入上采样层,充分利用每时刻纵向传播的空间特征,反馈到下一时刻的输入中。对比一般长短期记忆细胞单元,ST-DCSN所基于的时空细胞单元输入多了一个来自上一层上一时刻的输入和来自上一层当前时刻的空间细胞状态;在时序状态转移计算上,其加入了动态子细胞和静态子细胞来控制与衰减状态变化相关的信息输出。其中,同一层上的水平数据流动有隐藏状态和时序细胞状态,相邻层上的垂直方向上数据流动有隐藏状态和空间细胞状态;在层次l和时间步t上(l≥2,t≥2)会有来自层次l-1 的上一时间步t-1 隐藏状态作为当前的输入,结合来自层次l-1的当前时刻t的隐藏状态,在动态子细胞中,经衰减状态自差分算法计算出动态保留项,经由动态隐藏状态传递到静态子细胞,提取衰减不变信息,表示当前时刻衰减状态中的不变量,即最大程度不受其他因素影响,能反映衰减过程的静态信息,记作,代表l层上时刻t的静态子细胞隐藏状态。为了保证相邻时刻纵向上的空间细胞信息传递,最后一层的空间细胞状态需要进行上采样以反馈到下一时刻第1层的细胞输入中。在最后一层细胞循环体会输出提取到的时空复合特征,经过全局池化层后得到一维的特征向量。

图2 时空双细胞状态网络结构Fig.2 Spatial temporal-dual cell state network structure
1.2.1 时空卷积长短期记忆细胞体
ST-DCSN模型中的时空卷积长短期记忆细胞体具有静态和动态两种子细胞状态,也称为细胞中的细胞(COC),每次时序状态转移涉及两次转移计算,从而得出最终的时序细胞状态。由于空间信息亦需要在相邻时刻细胞单元上进行传递,所以在经典的长短期记忆网络基础上加入了空间细胞状态,负责对空间特征的状态在空间维度和时间维度上进行维护。
时序细胞状态的计算过程为
式中:Ot为模型总输出门;Wxo、Who、Wco、Wmo为上述输出门对应计算中可训练的权值参数,W1×1为卷积核大小为1 的可训练权值参数;为可训练的偏置参数。
式中,τUpsampling指上采样算法。
1.2.2 动态子细胞体
动态子细胞体的主要功能是计算状态自差分项,即接收上一层的当前时刻和上一时刻的隐藏状态作为输入。然后计算两者的差,作为最终细胞体的输入。相邻时刻状态的差值作为该时刻的差分动态值,即将衰减状态变化中的非静态部分特征提取出来,其中就包括需要保留的衰减状态变化信息和干扰信息,然后经过门控机制将二者分离,留下需要保留的与状态变化相关的信息,由此动态子细胞体的工作完成,输出是动态子细胞状态和隐藏状态。其中动态子细胞状态需要继续在水平方向上传播到下一时刻的动态子细胞体,隐藏状态作为输入进入静态子细胞体中进行下一步的计算。
动态子细胞隐藏状态的计算过程为
1.2.3 静态子细胞体
静态子细胞体负责接收来自上一时刻COC 细胞体的总时序状态,以及来自当前时刻动态子细胞体的隐藏状态,对两者进行卷积求和,经过门控机制得到静态子细胞状态和隐藏状态。其中,静态子细胞的隐藏状态根据公式参与当前COC细胞体时序状态的计算,形成最终时序细胞状态。
静态子细胞隐藏状态的计算过程为
2 基于ST-DCSN的轴承寿命预测
基于时空双细胞状态的轴承剩余使用寿命预测方法流程如图3所示。首先,利用传感器技术获得轴承运行过程中的振动传感信息,然后将得到的传感信息进行相关的数据预处理操作并进行规范化数据处理;其次,构建时空双细胞自适应感知网络ST-DCSN,进行参数初始化后开始训练模型,即将预处理后提取到的粗特征输入到该网络中提取深层特征,最终的特征经过剩余使用寿命预测网络输出RUL 预测值,并经过反向传播算法计算各层的梯度,更新网络参数。训练完毕后,在测试数据上进行线上测试和性能评估,图3中给出了一个示例。

图3 基于ST-DCSN的RUL预测流程图Fig.3 Flow chart of RUL prediction based on ST-DCSN
2.1 数据预处理
本文采用轴承的振动传感数据作为模型的输入,由于不依赖任何预处理操作而直接将原始信号作为输入,因此可以实现更进一步的端到端预测。
原始数据在被采集后需要进行规范化处理,本文采用的是最小-最大规范化(Min-Max Normalization)得到规范化后的数据样本,并将样本数据值映射到[-1,1]范围内。
式中,xmax、xmin分别为一次采样数据样本中的最大值和最小值。
2.2 模型构建与训练
ST-DCSN的模型主要由时空双细胞特征提取网络以及剩余使用寿命预测器构成。其中剩余使用寿命预测器是一个多层全连接网络,以特征提取网络提取到的高维时空隐藏特征作为输入,最终输出剩余使用寿命预测结果。如图3 所示,ST-DCSN 在经过多层堆叠的卷积长短期记忆细胞及迭代窗口大小的时间步后,得到了提取到的时空复合特征,再经过一个全局池化层后,输出的是特征f∈R1×c×w,其中c为通道数,w为输入时间窗大小。在相邻时间步之间进行空间信息传递过程中,上采样算法采用的是线性插值算法。全局池化后的特征在平整化后作为最后的剩余使用寿命预测器的输入,输出得到最终的剩余使用寿命预测值,本文采用的剩余使用寿命预测器是3层全连接神经网络。
ST-DCSN模型训练的输入数据是以滑动窗口的方式构建,窗口大小为w,损失函数采用回归任务常用的均方误差(MSE,LMSE)。
模型参数更新采取的是神经网络梯度下降反向传播(BP)策略。
式中:θ为网络参数;θ*为更新后的网络参数;α为学习率;∇LMSE(y)为网络输出关于均方误差损失的梯度。
2.3 评价指标
采用常见的回归性能度量指标根均方误差(RMSE)、平均绝对误差(MAE)和统计相关性度量指标R2,以及PHM2012 比赛官方所给的RUL 预测打分函数[28],分别表示为RRMSE、RMAE、RR2、RScore,该4 种指标的评价标准分别为越小越好、越小越好、越大越好、越大越好。
式中,ξi反映了某时刻的预测百分比误差。RScore是一种双边不对称的函数,PHM比赛主办方的初衷是让预测百分比误差尽可能是正值,即出现误差时刻真实值要大,鼓励适当的“预测提前”。
2.4 预测结果平滑
由于轴承振动信号属于非平稳信号,直接采用深度网络对其进行特征提取往往会给预测结果带来一定的非确定性。为了尽可能降低这种非确定性,一般会采用平滑操作,本文采用的是霍特二次指数平滑方法得到平滑预测值+h∣t。
式中:α′、β为平滑系数;h为常量,一般取1;xt为时间序列;+h∣t为平滑预测值。
3 实验验证
本文实验软件环境采用Linux Ubuntu20.04 操作系统、Pytorch-1.11。硬件环境采用Intel Core i7-10700KF CPU,内存为16 GB,NVIDIA GTX-3080 GPU,显存为10 GB。
3.1 实例研究Ⅰ:FEMTO-ST轴承数据集
3.1.1 数据介绍
本实例采用PHM2012 比赛所用数据[28]。该数据采集自法国FEMTO-ST 实验室的PRONOSTIA 实验平台,如图4所示,主要用到水平和垂直方向加速度传感器采集的轴承振动信号。本文用到的数据集工况状态类型如表1所示,用作训练的数据集有工况1、2对应的前5个轴承的数据集,对应的最后两个轴承的数据集B1_6、B1_7以及B2_6、B2_7作为测试集,取对应评价指标的平均值,用于验证模型的预测性能。因此,所使用的数据样本是每个采样段的两个方向振动数据,大小为2×2 560×1。

图4 FEMTO-ST数据集的PRONOSTIA实验平台Fig.4 PRONOSTIA experimental platform for FEMTO-ST dataset
3.1.2 模型训练
在模型的训练过程中,以滑动窗口的方式构建输入数据,窗口大小为w=7,这是通过实验得到的最佳窗口大小值。空间子细胞状态在每个时间步后的信息需要回传至下一时间步作为输入,因此,模型每一层卷积核数设置为32,大小为8,步长为1。剩余使用寿命预测器的全连接网络的神经元数量分别是32、16、1。批处理大小因计算资源限制,设置为32。为了让模型更好地收敛,学习率和训练轮数分别设置为0.000 05 和50,除了RUL 预测器的输出层,其余层激活函数均采用ReLU 激活函数。具体网络参数和训练超参数如表2所示。
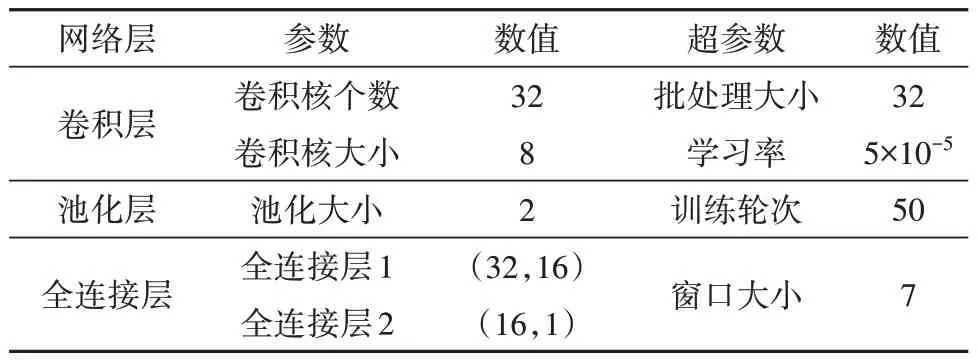
表2 ST-DCSN网络训练的超参数Table 2 Hyper-parameters of ST-DCSN
3.1.3 实验结果与分析
为了测试本文提出的ST-DCSN模型的性能,本实验分别与近年来优秀的直接采用原始信号作为输入的时序模型(TCN-RSA[29]、CNN-CBLSTM[30]、RCNN[20]、CLSTM[26]、LSTM 以及经过改进的MSCNN[9]方法)进行比较。其中,TCN-RSA 是采用多层时序卷积神经网络以及自注意力机制的轴承剩余使用寿命预测方法,其通过8层堆叠的时序卷积块提取特征;CNN-CBLSTM 是一种经4层堆叠的卷积神经网络来进行空间特征粗提取,接着用2层双向卷积长短期记忆网络进一步提取时空特征的方法;RCNN 是一种结合了卷积操作的门控循环单元网络以及采用了蒙特卡洛不确定性预测的方法,其堆叠4 层卷积循环网络进行特征提取以及3 层全连接进行RUL预测;CLSTM是一种结合了卷积操作的长短期记忆网络预测方法,其经过4 层堆叠卷积LSTM 层提取数据的时序和空间信息,最后同样是通过一个全连接层输出预测值,是本文模型构建的基础方法,本文在其基础上引入了差分链接、空间、动静态子细胞;LSTM 采用的是24个时域、频域特征[22],窗口大小等与ST-DCSN相同,隐藏层神经元数为16,后接一个3层全连接层作为RUL预测器;多尺度卷积神经网络MSCNN 是一种堆叠卷积网络,其中倒数第2层池化后的结果与最后一层卷积结果共同经过平坦层特征拼接得到输出特征。
从表3 可以看出,对于FEMTO-ST 工况1 数据集,ST-DCSN 模型相比起近年来的优秀模型,在4 个性能指标上除两个指标外,经过二次指数平滑后的预测值均位列第一。落后的指标R2 反映的是回归任务中预测值与真实值的回归相关性程度,由于ST-DCSN对时空信息比较敏感,会在衰减前期进行保守预测,所以回归性相对减弱,故会导致R2指标不足。但是,在实际场景中,往往是需要进行保守预测来减少因过度预测造成的损失,因此STDCSN 的预测是相比较为符合设备预后管理问题中偏向于提前预测的需求,这便解释了ST-DCSN的预测结果在Score指标上会取得更高的值,在R2上会相对较低。B1_7 的原始预测值和经过二次平滑后的结果如图5所示,由图可知经过平滑后能得到较好的拟合效果。另外,从图6 中可以看到,STDCSN的预测曲线的趋势性是在几个方法中最强的,且波动性较小,同时体现在根均方误差指标中是最小的。更重要的是,在PHM 中设备生命末期的预测精度是很重要的,由于轴承在生命末期会发生衰减突变,造成预测结果波动,而ST-DCSN于多种方法中在生命末期的拟合程度是最强的,波动性是最低的。对于工况2 数据集,从表4 可以看出,STDCSN 能够在4 项性能指标上取得第一,平均性能指标超过了性能优秀的TCN-RSA以及RCNN,这得益于时空特征的深层融合,使得预测结果回归性能更优,在经过平滑后基本在真值附近,如图7所示的B2_6预测结果。
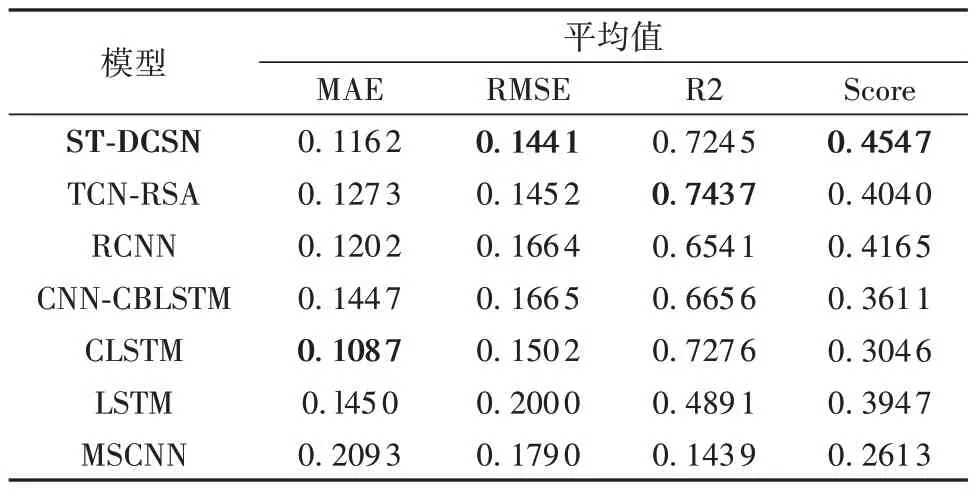
表3 ST-DCSN 在FEMTO-ST 的B1 数据集上各模型性能指标对比Table 3 Comparison of performance indicators of ST-DCSN models on FEMTO-ST B1 dataset

表4 ST-DCSN 在FEMTO-ST 的B2 数据集上各模型性能指标对比Table 4 Comparison of performance indicators of ST-DCSN models on the FEMTO-ST B2 dataset

图5 ST-DCSN在FEMTO-ST数据集B1_7上的预测曲线Fig.5 Prediction curve of FEMTO-ST dataset B1_7 by ST-DCSN

图6 各种方法在B1_7上的预测结果对比Fig.6 Comparison of forecast results of B1_7 by various methods

图7 ST-DCSN在FEMTO-ST数据集B2_6上的预测曲线Fig.7 Prediction curve of FEMTO-ST dataset B2_6 by ST-DCSN
在消融实验中,本实验将对空间细胞状态、动态和静态子细胞分别裁剪来进行消融,分别是完全版本的ST-DCSN、去除空间细胞状态的ST-DCSN、去除动态和静态子细胞的ST-DCSN。从表5 可以看出,去除空间细胞状态时,4 个指标均比完全版本的ST-DCSN差;去除动态子细胞和静态子细胞状态的实验中,4 个指标均比完全版本的ST-DCSN 差。总的来说,完全版本的ST-DCSN在各指标上均比消融实验组更优。
对于滑动窗口大小对预测性能的影响,本文分别设置了窗口大小为3、5、7、9 的多组实验,经过重复实验得到的实验效果如图8所示。从图中可知,当窗口大小设置为7时,模型能获得相对较好的预测性能。
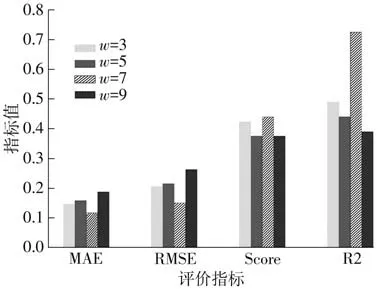
图8 输入窗口大小对预测性能指标的影响Fig.8 Influence of different window sizes on prediction performance indicators
另外,本文在对B1_7预测均值结果进行二次指数平滑操作上进行了平滑因子α′和趋势因子β对预测结果影响的实验探究。分别将平滑因子和趋势因子设置为0.05、0.10、0.25、0.50、0.75、1.00,可视化结果如图9、图10 所示。从图中可以看到,当平滑因子和趋势因子同时偏大或偏小时预测结果的根均方误差越大,说明趋势性对于根均方误差影响较大。均绝对误差受到两因子的影响比较平稳,只有在趋势因子较大时会出现较大误差值,因此,需找到一个适宜的值使得预测平滑结果更接近真值。

图9 平滑因子α'和趋势因子β对均绝对误差的影响Fig.9 Influence of smoothing factor α' and trend factor β on MAE

图10 平滑因子α′和趋势因子β对根均方误差的影响Fig.10 Influence of smoothing factor α' and trend factor β on RMSE error
3.2 实例研究Ⅱ:XJTU-SY轴承数据集
3.2.1 数据介绍
本实例采用的数据集来自西安交通大学-昇阳科技轴承加速实验平台[31],如图11 所示。该实验采用了15个LDK UER204滚珠轴承,在3种不同工况下对轴承的全寿命周期数据进行采集。该数据集包含了3种工况下的15个滚动轴承的全寿命周期振动信号,且明确标注了每个轴承的失效部位,与FEMTO-ST 类似,主要也是用到在其上安装的水平和垂直方向加速度传感器采集的轴承振动信号。每个运行工况下均有5个子集,本文采用的具体数据集工况状态类型如表6 所示。本实验采用工况2 中的数据,前3个子集作为训练集,最后两个轴承的数据集作为测试集,用于验证模型的预测性能。因此,所使用的数据是每个采样段的两个方向振动数据,大小为2 × 32 768 × 1。

表6 XJTU-SY轴承数据集工况状态类型Table 6 Working condition of XJTU-SY bearing dataset
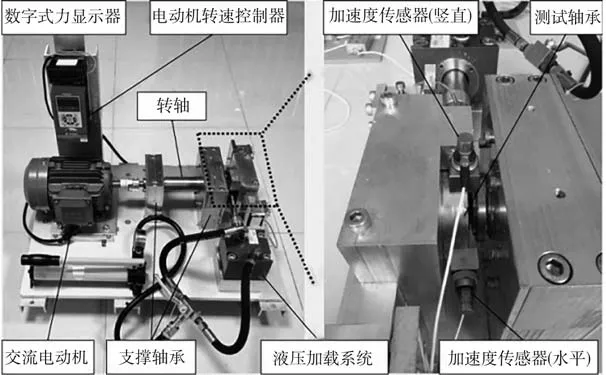
图11 XJTU-SY数据采集用的轴承加速寿命试验台Fig.11 XJTU-SY accelerated bearing life experimental platform for data collection
3.2.2 模型训练
在数据预处理上,由于该数据集样本采样点数较多,无法以滑动窗口的方式构建输入数据,故设窗口大小为w=7。在超参数设置上,由于XJTU-SY数据集原始信号采样点更多,受限于硬件内存,批处理大小设置为4;鉴于数据样本点更多,模型收敛慢,训练轮次设置为500,以及池化层池化大小设置为4,其余参数与FEMTO-ST实例相同。
3.2.3 实验结果与分析
为了测试本文提出的ST-DCSN模型的性能,本实例分别与近年来优秀的RUL 预测模型(TCNRSA[29]、CNN-CBLSTM[30]、RCNN[20]、CLSTM[26]、LSTM 以及经过改进的MSCNN[9]方法)进行预测性能比较。其中,CNN-CBLSTM、RCNN、CLSTM 均以原始振动数据作为网络输入,其超参数和输入均与ST-DCSN相同。
从表7 中可以看出,ST-DCSN 模型相比近年来的优秀方法,经过二次指数平滑后的预测性能指标平均值在4个性能指标上均是最优的,这得益于双细胞模型方法和状态自差分算法。ST-DCSN能在轴承振动信号中提取到一般的时间和空间特征并经过深层网络的自适应融合,因此ST-DCSN会得到更好的预测结果。这在另一个不同类型不同工作负载的真实轴承数据集上证明了本文方法的优越性。图12所示为ST-DCSN在B2_4上的预测结果,可以看出,在轴承衰减前中期开始拟合效果逐渐提升,并在生命末期取得了较好的预测效果。
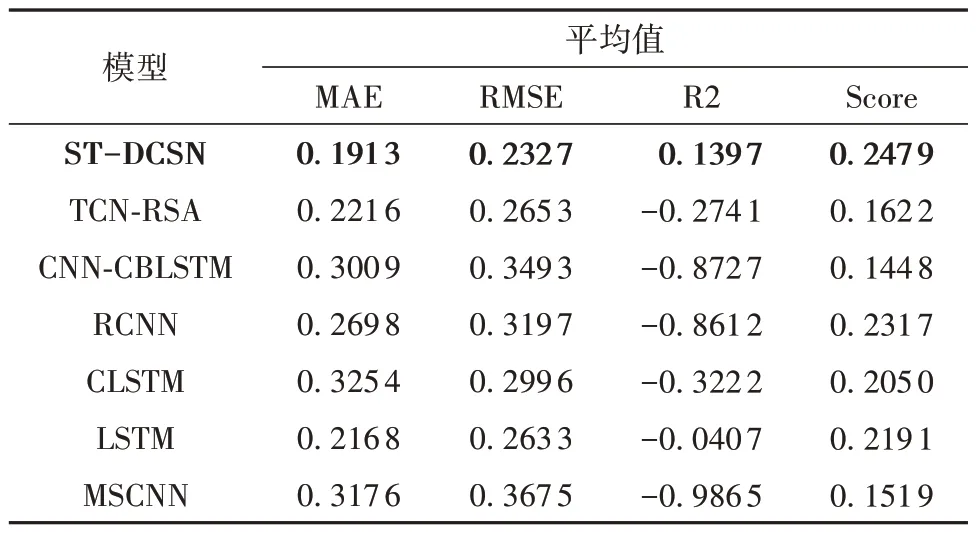
表7 ST-DCSN在XJTU-SY数据集上各模型性能指标对比Table 7 Comparison of performance indicators of ST-DCSN models on XJTU-SY dataset
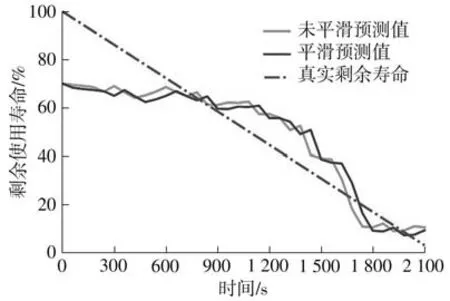
图12 XJTU-SY数据集B2_4上的预测曲线Fig.12 Prediction curve of XJTU-SY dataset B2_4
4 结论
本文提出了一种基于双细胞状态自适应感知的剩余使用寿命预测方法,通过一种双细胞自适应感知特征提取神经网络ST-DCSN,解决在PHM 中轴承的剩余使用寿命预测问题中时序和空间特征难以有效提取的问题,从而提高预测准确性。为了验证该方法的性能,本文分别在FEMTO-ST 和XJTU-SY两个真实轴承数据集上进行实验验证,均得到了较为优秀的效果。这要归功于ST-DCSN优秀的时间和空间特征提取能力,其在原有LSTM 的时序细胞状态的基础上引入了新的空间细胞状态,在深层空间特征提取过程中以空间细胞来保持对关键空间特征的记忆,减少在空间维度上随着网络的层次加深而丢失空间信息。通过对原卷积长短期记忆细胞的改进,在一定程度上加强了不同层之间的空间信息和时序信息的融合,在空间提取方向上进行了状态的保存,增强了空间维度的重要信息保留程度。通过消融实验,本文证明了所引入的空间细胞状态和两个子细胞状态对预测性能提升的必要性,而且还探究和分析了不同参数对预测结果的影响。
本文虽然实现了对卷积长短期记忆网络模型中空间特征的进一步挖掘,以及其与时序特征的融合,在层之间保留关键空间信息,但预测结果仍存在局部抖动和波动问题,即预测的不确定性不可忽略,因此需要平滑操作。在轴承生命末期有一定的抖动说明时序信息和空间信息的融合效果仍有上升的空间,另外对于非平稳的原始信号对预测结果带来的不确定性也需要关注。近年来亦有较多关于不确定性的探究,接下来的工作会考虑引入不确定性预测方法如蒙特卡洛方法、深度贝叶斯网络等方法进行研究,以探索出一种尽可能降低时空信息融合不确定性的方法。

