多轴机器人系统输出反馈有限时间同步位置控制

季祥 王海红 翟天嵩 屈保中 李鹏

（1.西安电子科技大学 机电工程学院，陕西 西安 710071；2.河南工业职业技术学院 自动化工程学院，河南 南阳 473000；3.南阳理工学院 智能制造学院，河南 南阳 473004）

机器人的位置控制一直被认为是机器人控制领域最基本、最简单的目标。随着现代科学技术的飞速发展和工农业自动化水平的不断提高，人们对机器人的控制精度提出了越来越高的要求［1-3］。由于一般很难从一个实用的机器人系统同时获得关节的位置信息和速度信息［4-5］，加之PD 和PID 型的控制器具有概念简单、控制器参数整定规则明晰和易于工程实现等优点，涌现出一批专家和学者致力于机器人的输出反馈PD+/PID 位置控制研究，并获得了渐近稳定性的结论［6-11］。

相比于渐近稳定控制，有限时间稳定控制能驱动系统的状态在有限时间内趋近稳定平衡点，且能获得更快的收敛速度、更高的控制精度和更强的抗干扰性［12-13］，故部分学者应用几何齐次性技术开展多轴机器人系统的输出反馈有限时间PD+/PID 位置控制研究，并取得了丰硕的成果［14-19］。

虽然上述研究取得了较好的控制效果，但所提出的输出反馈有限时间位置控制算法缺乏对各个轴间的协调控制。轴间的协调性是影响机器人系统高精度运动的重要因素，同步控制技术是研究轴间协调性的关键。近年来，将交叉耦合控制技术［20］应用于机器人系统的研究受到越来越多的关注［21-27］。具体地说，Sun 等［21］对多轴机器人系统进行了交叉耦合控制，提出了PD 型位置同步和轨迹跟踪同步控制方法；Sun和Wang［22］将同步位置控制算法应用到了移动机器人编队控制上，获得了较好的控制效果；Su 等［23］利用交叉耦合技术针对并联机器人系统提出了非线性PD同步位置控制器；Shang等［24］提出了绳索牵引并联机器人系统的自适应交叉耦合控制策略，获得了高精度的轨迹跟踪控制效果；文献［25］研究了多轴系统的非线性PID 同步位置控制算法，实现了系统的高精度同步控制。文献［21-25］所提出的同步控制算法保证了闭环系统的全局渐近稳定性。为了进一步提高机器人系统的控制精度，满足高精度运动要求，文献［26］结合有限时间控制思想提出了基于交叉耦合控制技术的有限时间PD+/PID稳定同步协调位置控制策略。但文献［21-26］的控制器实现均依赖于系统的位置信息和速度信息的全状态反馈。为了释放控制器对速度信号的依赖，文献［27］研究了只基于位置测量的多轴机器人系统输出反馈PD+/PID 同步位置控制策略，但只得到闭环系统渐近稳定性的结论。

本文在前期所提出的多轴机器人系统输出反馈位置控制［19］的基础上，进一步提出了输出反馈有限时间PD+同步（OFPD+S）位置控制策略，并应用Lyapunov稳定性理论和几何齐次性技术严格证明闭环系统的全局有限时间稳定性。与文献［14-19］所述输出反馈有限时间控制相比，本文所提出的控制算法引入了非线性同步控制项，能实现各轴间的同步协调运动，进而提高系统整体性能和运动精度；相比于全状态反馈的同步控制算法［21-26］，所提出的非线性PD+控制能实现仅依赖于关节位置测量的有限时间输出反馈同步位置控制；与渐近稳定的输出反馈同步位置控制［27］相比，所提出的同步控制能保证闭环系统的全局有限时间稳定性，提高系统的瞬态响应速度和稳态定位精度。本文还通过数值仿真验证了所提出的控制算法的有效性和可行性。

1 预备知识

1.1 有限时间稳定性理论

本文依据的有限时间稳定性理论［4，14］如下所示。

定义1平衡点

非线性系统

的平衡点x*∈Rn是指一旦系统的状态等于x*，则它就一直等于x*。可以通过求解方程

获得系统的平衡点。

进一步地，若非线性系统（1）的f不显含时间t，那么得到式（3）所示时不变系统：

其中，f：U0→Rn在原点x=0 的一个开邻域内连续，并且有f(0)=0。假定对于任意的初始条件，系统（3）在向前时间有唯一的解。

定义2局部（全局）有限时间稳定平衡点

如果系统（3）的平衡点x=0 是Lyapunov 稳定的，且在原点的一个邻域U⊂U0内是有限时间收敛的，则系统的原点是局部有限时间稳定的平衡点。

进一步地，若U=Rn，则原点是全局有限时间稳定的平衡点。

定义3齐次向量场和齐次系统

设f(x)=(f1(x)，f2(x)，…，fn(x))T是一个连续的向量场，对于任意给定的ε＞0，如果有下式成立：

则f(x)称为具有齐次度d∈R 的齐次向量场，其中（r1，r2，…，rn）（ri＞ 0，i=1，2，…，n）称为扩张系数。

若f(x)是齐次向量场，则称系统（3）为齐次系统。

引理1局部有限时间稳定［4］

考虑系统

那么x=0 是系统（5）的局部有限时间稳定的平衡点。

引理2全局有限时间稳定［4］

如果一个系统是全局渐近稳定的和局部有限时间稳定的，则该系统是全局有限时间稳定的。

1.2 机器人系统模型及其主要特性

多轴机器人系统的动力学方程为

式中：q、、∈Rn，分别为关节的位置、速度和加速度矢量；H(q) ∈Rn×n为惯性矩阵；C(q，) ∈Rn×n为哥氏力和离心力矩阵；D∈Rn×n为各关节线性阻尼摩擦力矩阵，D一般为正定对角矩阵；g(q)∈Rn为重力矢量；τ∈Rn为控制力矩矢量。

系统（7）具有如下主要性质［4，14］。

性质1惯性矩阵H(q)对称正定且满足如下的有界性：

式中，λm(·)和λM(·)分别为对称正定矩阵的最小和最大特征值，符号‖ · ‖代表标准的欧式范数。

性 质2(q) -2C(q，) ∈Rn×n是反对称矩阵，即

式中，(q) ∈Rn×n为矩阵H(q)的一阶微分。

2 控制器设计

2.1 控制目标

本文的目标是对式（7）所示的多轴机器人系统设计输出反馈有限时间PD+同步位置控制（OFPD+S），即对于任意初始状态(q(0)，(0))和给定常值期望位置qd∈Rn，所设计的控制器能驱动闭环系统的位置误差和同步误差在有限时间内收敛到平衡点。

2.2 输出反馈有限时间同步位置控制器

为了便于控制器设计和稳定性分析，定义如下一些变量。

定义位置误差矢量e∈Rn如式（10）所示：

式中，qd与q分别为期望和实际关节位置。

同步误差E∈Rn定义为每个轴的位置误差与旁边相邻两个轴位置误差的差值关系，其关系如下［21］：

式中，E=(E1，E2，…，En)Τ为系统各个轴间的同步误 差，e=(e1，e2，…，en)Τ为系统的位置误差，T∈Rn×n为转换矩阵。需要特别说明的是，当i=1时，令i-1=n；当i=n时，令i+1=1。

对于任意矢量ξ=(ξ1，ξ2，…，ξn)Τ，易有下式成立：

易知转换矩阵T为对称半正定矩阵。

结合所定义的同步误差和位置误差，定义如下所示的耦合位置误差η∈Rn：

式中，I为n×n的单位矩阵，λ为和同步控制相关的正数，λ越大同步控制作用也越强。从式（13）易知，当η→0 时，有e→0 和E→0，即可实现各轴的同步控制效果。

对于位置控制而言，很容易进一步得到：

对于给定矢量z=(z1，z2，…，zn)T∈Rn，定义矢量函数Sig(·)α∈Rn为

式中，0 ＜α＜1，sgn(·)为标准的符号函数。

至此，利用定义的耦合位置误差（13）和矢量函数（15），本文所提出的考虑轴间同步控制的OFPD+S控制器可表述为

式 中：Kp=diag(kpi)，Kd=diag(kdi)，A=diag(ai)和B=diag(bi)，i=1，2，…，n，分别为对角正定的比例增益、微分增益和滤波器增益矩阵；qc∈Rn为辅助中间变量；υ∈Rn为估计速度矢量；Kη=diag(kηi)，i=1，2，…，n，为对角正定的同步控制增益矩阵；0 ＜α1＜1，α2=(α1+1)2。

将式（16）代入系统（7）并利用式（17）和（18），可得到如下所示的闭环系统动力学方程：

2.3 稳定性分析

定理1对于给定的多轴机器人系统（7），所提出的OFPD+S 控制器（16）-（18）能保证闭环系统（19）和（20）的全局有限时间稳定性。

证明定理1 的证明过程可分为3 步：首先利用Lyapunov 直接方法和LaSalle 不变性原理证明闭环系统的全局渐近稳定性；然后利用引理1证明闭环系统的局部有限时间稳定性；最后应用引理2得到定理1的结论。

（1）全局渐近稳定性

首先选取如下候选Lyapunov函数：

式 中，ei、υi和ηi分别为矢量e、υ和η的 第i个分量。

利用性质1 和0 ＜α1＜1，可以得到对于任意状态e、、υ、η∈Rn，候选Lyapunov 函数V是正定的和径向无界的。

V的时间导数为

将H(q)和的表达式（19）和（20）及式（14）代入式（22），并应用性质2，同时考虑位置控制的特性=，可以得到如下表达式：

由表达式（23）易知是半负定的。

综上可知V(e，，υ，η)是全局正定和径向无界的，其时间导数(e，，υ，η)是半负定的。

记G表示由(e，，υ，η)=0形成的子集，即

由方程（19）和（20）、式（13）以及函数Sig(·)α的定义（15）可进一步有e=0，η=0。这表明对于由=0，υ=0（也就是(x)=0）定义的子集G来说，G内的最大不变集M仅包含原点。因此，应用LaSalle 不变性原理［28-31］，对于任意初始状态(q(0)，(0)，υ(0)，η(0))，当t→∞时，系 统（19）和（20）的状态变量全局渐近收敛到(q=qd，=0，υ=0，η=0)。

（2）局部有限时间稳定性

利用Hong等［14，32］给出的指导思想和引理1证明闭环系统的局部有限时间稳定性。

利用定义1 给出的平衡点求解方法（式（2）），令方程（24）的右边等于0，易解出x=0是其唯一的平衡点。但系统（24）不是齐次的，为了应用引理1，把式（24）改写为

至此，系统（25）具备了引理1 的表达式（5）的形式，于是由式（25）可容易得到如下系统：

根据齐次系统的定义3可知，若系统（28）为齐次系统，则应满足如下条件：

接下来证明闭环系统（25）（也就是系统（24））的局部有限时间稳定性。

首先证明x=0是系统（28）的渐近稳定平衡点。为此，构建如下正定正则的候选Lyapunov函数：

式中，x1i、和x4i为矢量x1、x3和x4的第i个分量。

利用性质1 和0 ＜α1＜1 可知，对于任意状态(x1，x2，x3，x4)，候选Lyapunov 函数V1是正定的和径向无界的。

V1沿齐次系统（28）的时间导数为

式（31）的推导利用了位置控制性质(qd)=0。根据表达式（31），可知是半负定的。

至此可知Lyapunov 函数V1(x1，x2，x3，x4)是全局正定和径向无界的，其时间导数(x1，x2，x3，x4)是半负定的。由=0 可有=0，即x3=0。由系统（28）和定义（15）可进一步有x2=0，x1=0 和x4=0。至此，应用LaSalle 不变性原理［28］可知，原点是齐次系统（28）的全局渐近稳定平衡点。

现证明由式（26）定义的(x) 满足引理1 的条件（6）。注意到H-1(x1+qd)和C(x1+qd，x2)都是光滑的［14］且d＜0，于是有：

对(x1，qd)的每一个分量应用中值定理［14］有：

注意到式（34）的推导利用了当0 ＜α1＜1 时，r1-d-r2=2(1 -α1)＞0 的事实，因此，对任意的x=∈R4n有：

根据引理1，可知闭环系统（25）（也就是系统（19）和（20））是局部有限时间稳定的。

（3）全局有限时间稳定性

结合前面两个步骤的证明，应用引理2易知闭环系统（19）和（20）是全局有限时间稳定的。证毕。

注解1与Kelly提出的输出反馈PD+［6］（OPD+）控制（36）和（37）相比，所提出的OFPD+S 控制器的优点体现在：非线性函数的引入提高了系统的瞬态响应速度和稳态定位精度，并保证了闭环系统的全局有限时间稳定性；同步控制项的引入实现了多轴机器人系统各轴间的同步协调运动，提高了系统整体性能和运动精度。相比之下，Kelly 提出的OPD+［6］控制没有考虑轴间的同步协调控制，且只得到了渐近稳定性的结论。

注解2与渐近稳定输出反馈PD+同步［27］（OPD+S）位置控制（38）相比，所提出的OFPD+S 同步控制保证了闭环系统的全局有限时间稳定性，提高了系统的瞬态响应速度和稳态定位精度。

值得说明的是，OPD+S［27］控制（38）的滤波器表达式与式（37）相同。

注解3由OFPD+S 控制器（16）和耦合位置误差η的定义（13）可以看出，同步常数λ越大同步控制作用越强，同步效果越好。但λ越大所需的控制力矩也越大，进而可能会影响或限制系统性能的获得。由此可见，同步常数λ对同步控制起着非常重要的作用，故要结合实际系统选择适中的λ值。

注解4令所提出的OFPD+S 控制器（16）中的参数λ=0 和Κη=0，则可得到不含同步误差的输出反馈有限时间PD+［19］（OFPD+）位置控制器：

值得指出的是，所提出的OFPD+S 控制器和OFPD+［19］控制器是有明显区别的。所提出的OFPD+S控制是利用位置误差e、速度估计υ和耦合位置误差η作为反馈信息的，而OFPD+［19］控制仅利用位置误差e和速度估计υ作为反馈信息，故所提出 的OFPD+S 控制能同时保证e→0，υ→0 和η→0，加速了同步误差E趋近于零，能获得令人满意的同步控制性能。

注解5所提出的OFPD+S 控制器的增益调节过程为：①选择λ=0 和Κη=0，通过反复试验，调节控制器参数Kp和Kd，以及滤波器参数A和B。②逐渐增加同步常数λ的值以便产生同步控制作用并试选λ值。③从0开始逐渐增加同步矩阵Κη以进一步加强同步控制的效果。值得说明的是，同步矩阵Κη与同步常数λ的选择相互依存，共同影响同步控制的程度，故第②步和第③步要综合考虑并反复试验选择。④再次微调控制器参数Kp和Kd以及滤波器参数A和B，以获得期望的控制精度和系统性能。

注解6本文所提出的控制策略同样适用于数控机床等多轴系统的同步控制，即具有一定通用性。

3 仿真分析

本节通过图1所示的3自由度机械臂［19］的数值仿真验证所提出的控制算法的有效性和可行性。系统的阻尼摩擦力矩阵D=diag（0.193，0.852，1.524）。

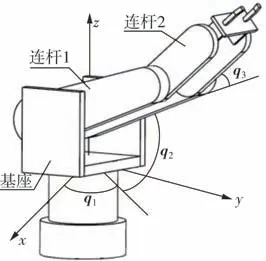
图1 3自由度机械臂系统Fig.1 Three-DOF robot manipulator

仿真1与渐近稳定控制OPD+［6］的比较

将所提出的OFPD+S 控制与Kelly 的不含同步控制项的OPD+［6］控制式（36）和（37）进行比较。将这两种控制器进行比较的依据是：它们具有相似的结构且均能实现机器人系统输出反馈稳定位置控制。

期望的关节位置选为：qd=(π，π，π)T（rad）。初始条件均选为零。采样周期取为T=1 ms。经反复调试，本文所提出的OFPD+S 同步位置控制器的参数选为α1=0.5，Kp=diag(12，12，12)，Kd=diag(11，11，11)，λ=0.2 和Kη=diag(14，14，14)，非线性滤波器的参数选为α2=(α1+1)2=0.75，A=diag(100，100，100)和B=diag(20，20，20)。为了比较的相对公平性，OPD+［6］控制的参数和所提出的有限时间OFPD+S 同步控制相同，但不包括参数α1、α2、λ和Κη。

图2给出了所提出的OFPD+S 控制和OPD+［6］控制的位置误差。图3为两种控制算法下的同步误差曲线。值得说明的是，图3（a）是为了便于和图3（b）进行比较而绘出的，而在OPD+［6］控制器表达式（36）中并不存在这样的同步控制项。图4给出了两种控制算法的控制力矩。

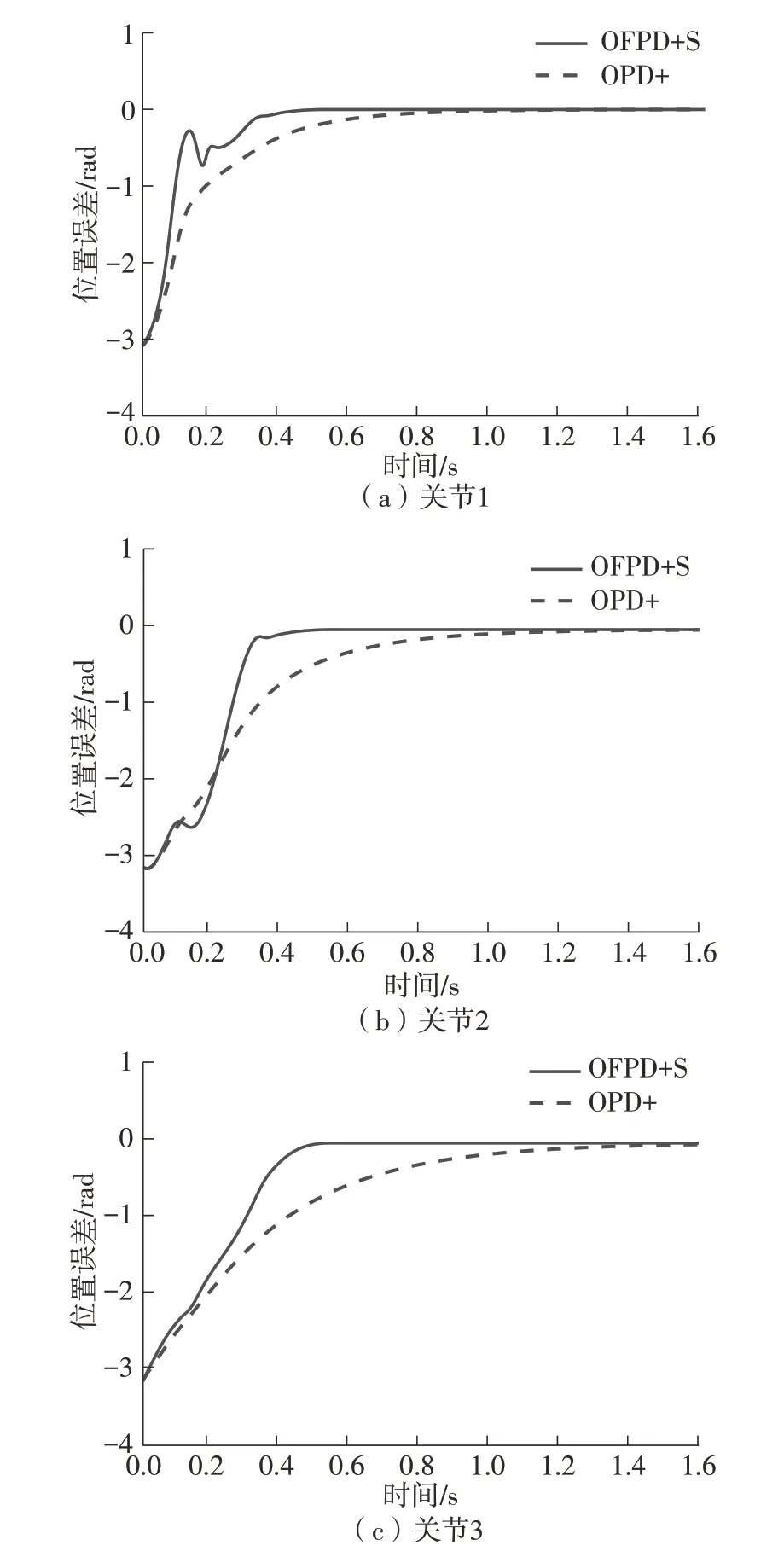
图2 OFPD+S和OPD+控制的位置误差Fig.2 Position errors of OFPD+S and OPD+control

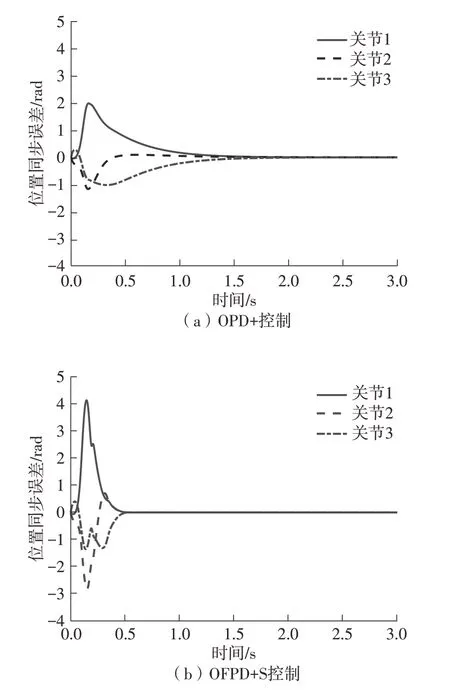
图3 OPD+和OFPD+S控制的同步误差Fig.3 Synchronization errors of OPD+and OFPD+S control

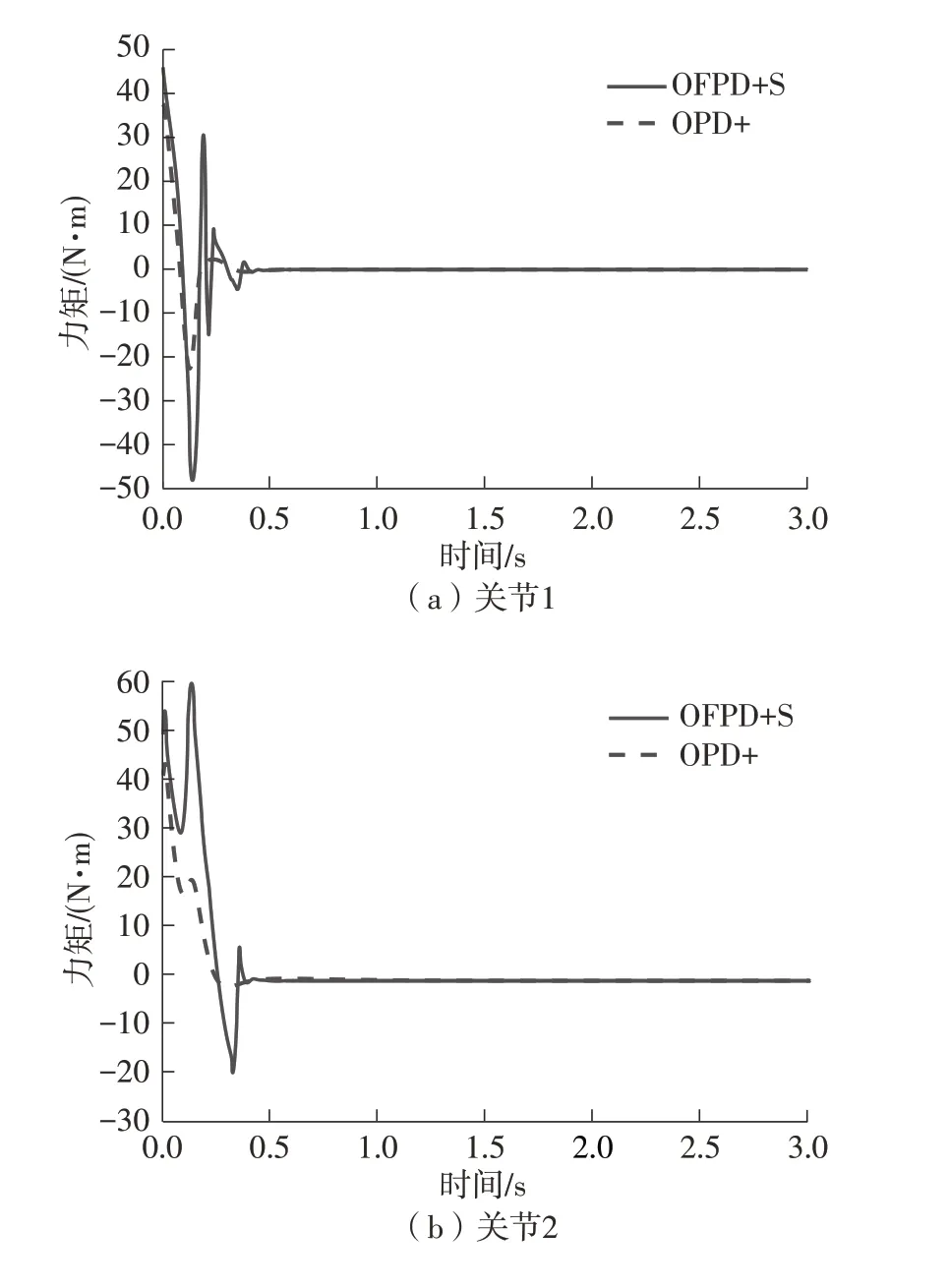
图4 OFPD+S和OPD+控制的控制力矩Fig.4 Input torques of OFPD+S and OPD+control

由图2和图3可以清楚地看出，经过初始的较大误差的暂态过渡过程之后，两种控制算法均能使机械臂的3个关节到达所期望的位置。但相比于渐近稳定的OPD+［6］控制，所提出的OFPD+S控制具有更快的响应速度、更少的调节时间和更高的稳态精度。此外，Kelly 提出的OPD+［6］控制使各关节达到期望位置的时刻分别为1、1.2和1.5 s左右，即3个关节到达期望位置的时刻不一致，运动不同步；而所提出的OFPD+S控制驱动3个关节达到所期望位置的时刻基本一致，均是0.5 s左右。由此可见，所提出的OFPD+S 同步控制由于在算法中包含了轴间的同步控制项，从而很好地实现了3个关节的同步运动控制。由图4 可见，OFPD+S 控制的控制作用较OPD+［6］控制的并没有增加很多，即所提出的OFPD+S 控制的优良系统性能的获得并不是以大大增加系统驱动力矩为代价的，这进一步显示了所提出的有限时间OFPD+S同步控制器的工程实用性和有效性。

仿真2与同步位置控制OPD+S［27］的比较

将所提出的有限时间OFPD+S 控制与渐近稳定的OPD+S［27］控制式（38）进行数值仿真分析。将这两种控制器进行比较的依据是：它们具有相似的结构且均能实现机器人系统输出反馈同步位置控制。

期望关节位置、初始条件、采样周期以及所提出的OFPD+S 同步控制器的参数与仿真1 相同。为了体现比较的相对公平性，OPD+S［27］的参数采用和OFPD+S的相同，但不包括参数α1、α2和λ。

图5 给出了所提出的OFPD+S 和OPD+S［27］控制的位置误差，图6为同步控制器OPD+S［27］作用下的同步误差，图7为两种控制算法下的控制力矩。

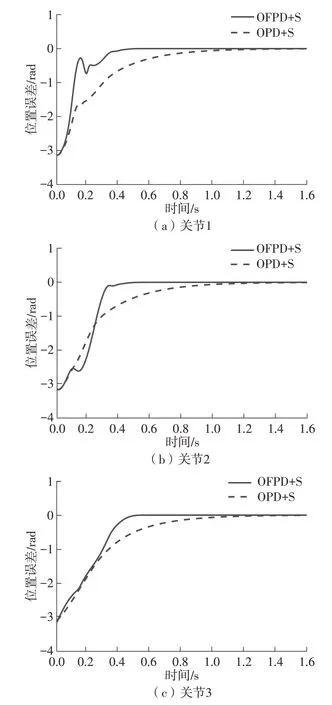
图5 OFPD+S和OPD+S控制的位置误差Fig.5 Position errors of OFPD+S and OPD+S control

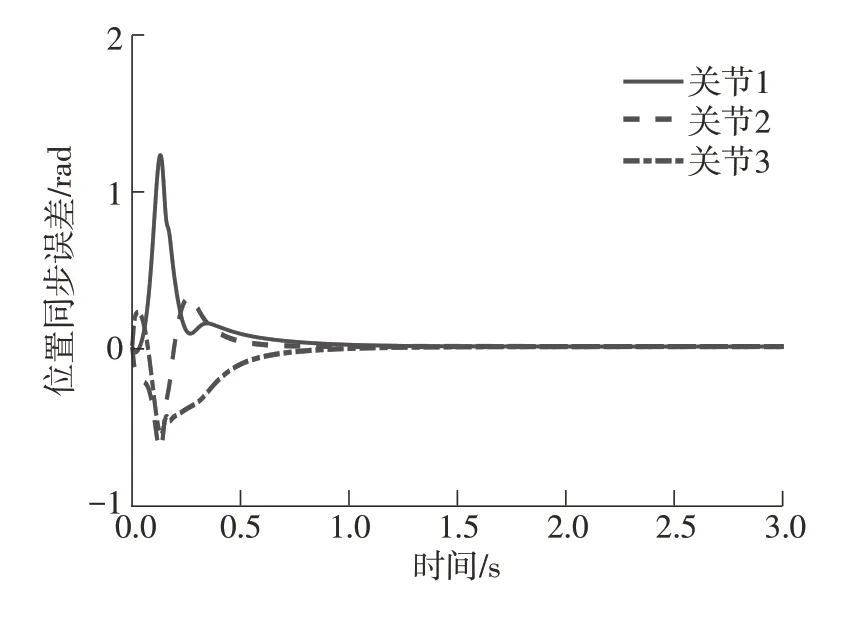
图6 OPD+S控制的同步误差Fig.6 Synchronization errors of OPD+S control

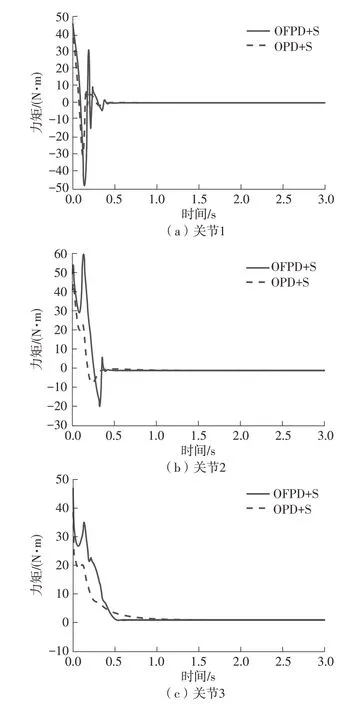
图7 OFPD+S和OPD+S控制的控制力矩Fig.7 Input torques of OFPD+S and OPD+S control

由图5可以看出，经过初始的较大误差过渡过程之后，两种控制算法均能很好地解决3个关节的位置控制问题，即运动到各自的期望位置。但相比于渐近稳定的OPD+S［27］同步控制，所提出的有限时间OFPD+S 同步控制具有更快的收敛速度和更好的稳态定位精度。对比图6和图3（b）可以看出，两种控制算法均能实现3个关节的同步位置控制，但所提出的OFPD+S控制器驱动3个关节达到期望位置的时刻（约0.5 s）明显比OPD+S［27］控制达到的时刻（约1.5 s）快，即所提出的有限时间OFPD+S控制的同步效果更好。由图7可进一步看出，所提出的OFPD+S控制的控制作用相比于OPD+S［27］控制并没有增加很多，即在不过多牺牲系统控制力矩的情况下，所提出的OFPD+S 控制器获得了更好的收敛速度和定位精度，以及优越的同步控制效果，进而提高系统的整体控制性能，更好地满足工程实际需要。

仿真3与有限时间控制OFPD+［19］的比较

进一步将所提出的输出反馈有限时间同步位置控制器OFPD+S 与不含同步误差的输出反馈有限时间OFPD+［19］控制器（39）进行仿真研究。将这两种控制器进行比较的依据是：它们具有相似的控制器结构且均能实现机器人系统输出反馈有限时间稳定位置控制。为了体现比较的相对公平性，OFPD+［19］控制器的参数选为和所提出的OFPD+S 控制器一致，但不包括参数λ和Κη。

图8 给出了所提出的OFPD+S 控制和OFPD+［19］控制的位置误差，图9为OFPD+［19］控制作用下的同步误差。值得指出的是，图9也是为了便于和所提出的OFPD+S控制进行比较而绘制的。图10描述了两种控制算法的控制力矩。

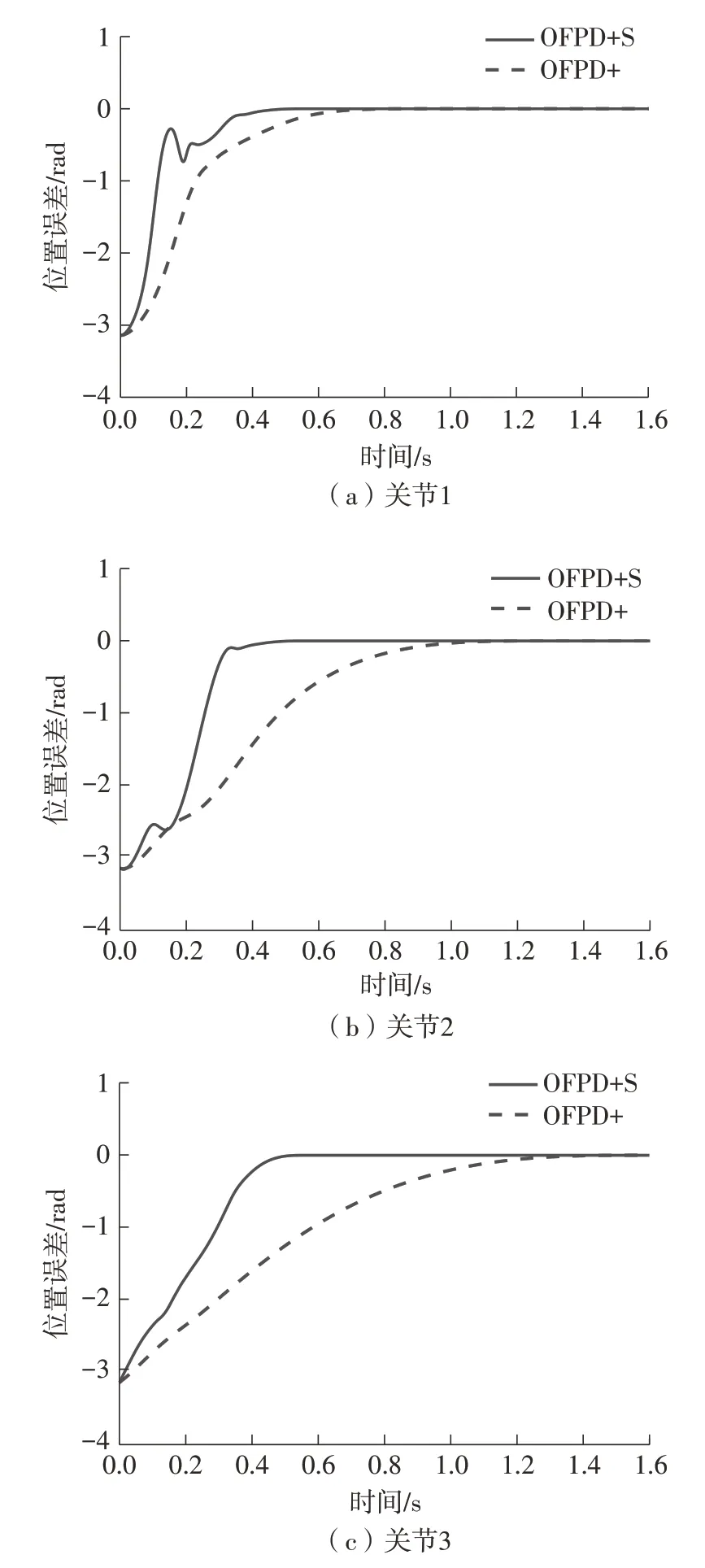
图8 OFPD+S和OFPD+控制的位置误差Fig.8 Position errors of OFPD+S and OFPD+control

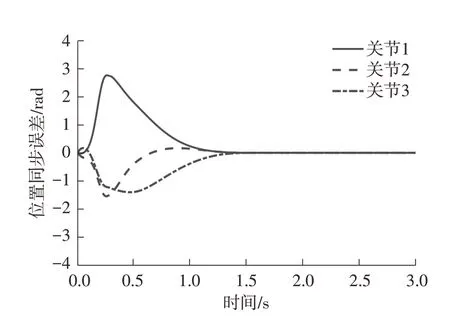
图9 OFPD+控制的同步误差Fig.9 Synchronization errors of OFPD+control

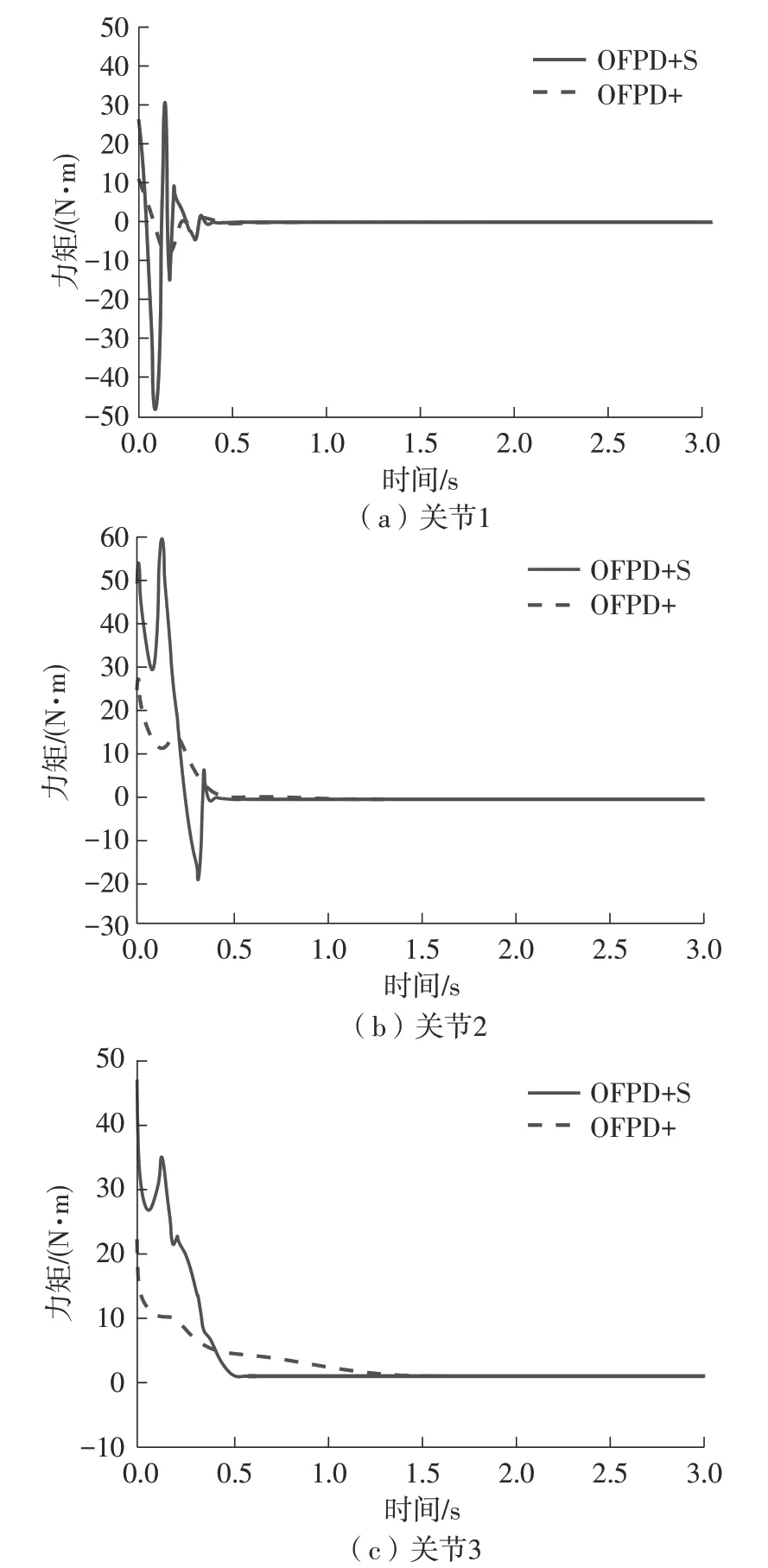
图10 OFPD+S和OFPD+控制的控制力矩Fig.10 Input torques of OFPD+S and OFPD+control

由图8可以看出，两种控制算法均能使机器人的3个关节到达所期望的位置，但所提出的有限时间OFPD+S同步控制较有限时间OFPD+［19］控制获得了更快的响应速度和调节时间。对比图9与图3（b）可知，在所提出的OFPD+S 控制器作用下，3 个关节的位置误差趋近于零的时刻基本一致（约0.5 s），达到了快速同步运动，而OFPD+［19］控制虽能保证3 个关节的位置误差趋近于零，但趋近零的时刻不一致（分别约为0.9、1.2和1.5 s），即3个关节的运动不同步。由此可见，所提出的含同步控制项的OFPD+S 控制相比于不含同步控制项的OFPD+［19］控制具有能保证3 个关节位置同步运动的优点。由图10可以看出，虽然所提出的OFPD+S控制在初始时刻的力矩相比于OFPD+［19］控制的略大，但所提出的OFPD+S 控制能获得更快的收敛速度和更好的同步效果，能大大提高系统的整体控制精度，获得更好的系统性能，能满足工程实际的需要。

仿真4同步常数λ对同步控制的影响

为了直观地说明同步常数λ对同步控制作用的影响，图11 和图12 分别给出了λ=0.1，0.5，1.05时所提出的OFPD+S 控制的同步误差和控制力矩。由图11和图12可以看出，随着同步常数λ的增大，3 个关节的同步误差向逐渐减小的方向变化，即同步常数λ越大同步效果越好；但随着λ的逐渐增大，在控制参数不变的情况下控制力矩会出现抖动。由此可见，应根据实际情况选择适中的同步常数λ。

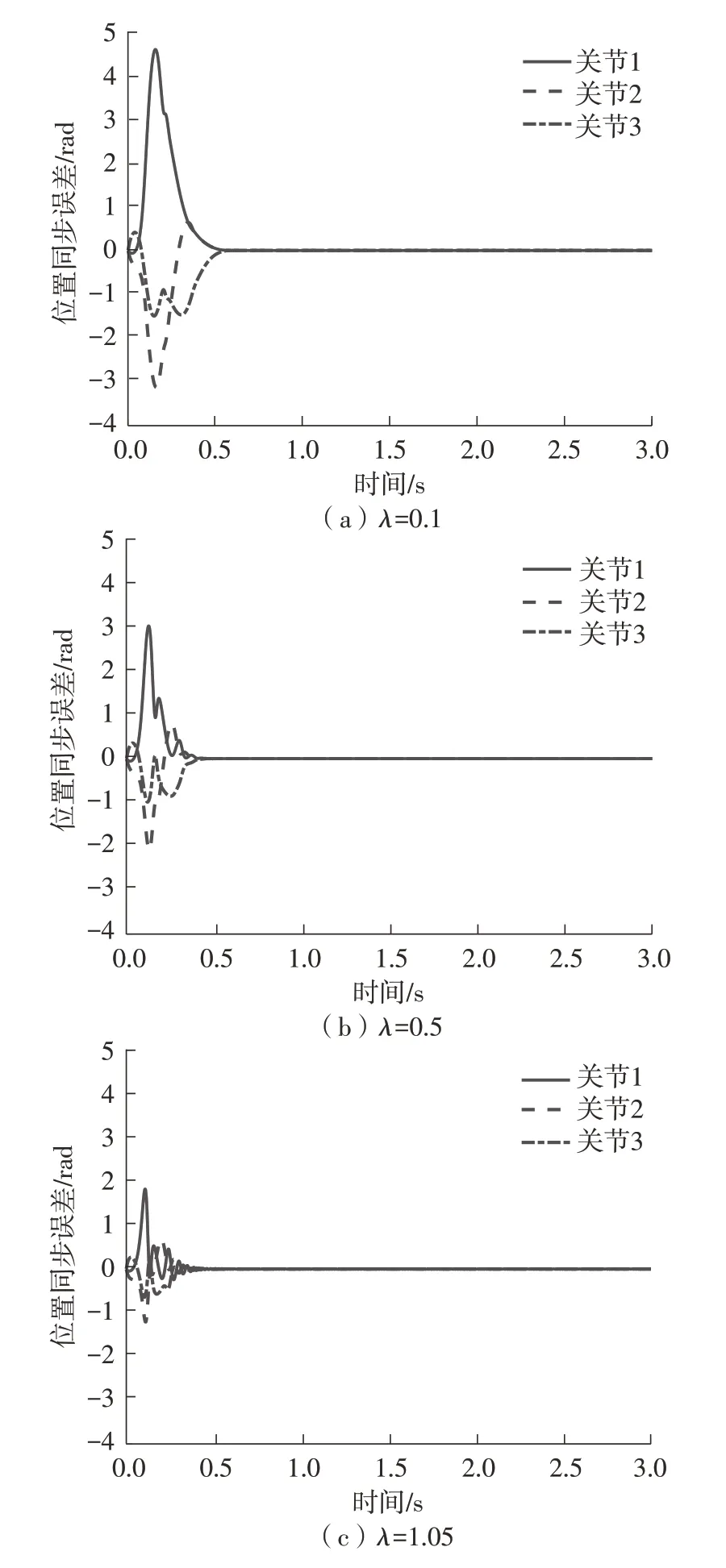
图11 不同λ时OFPD+S控制的同步误差Fig.11 Synchronization errors of OFPD+S control with different λ

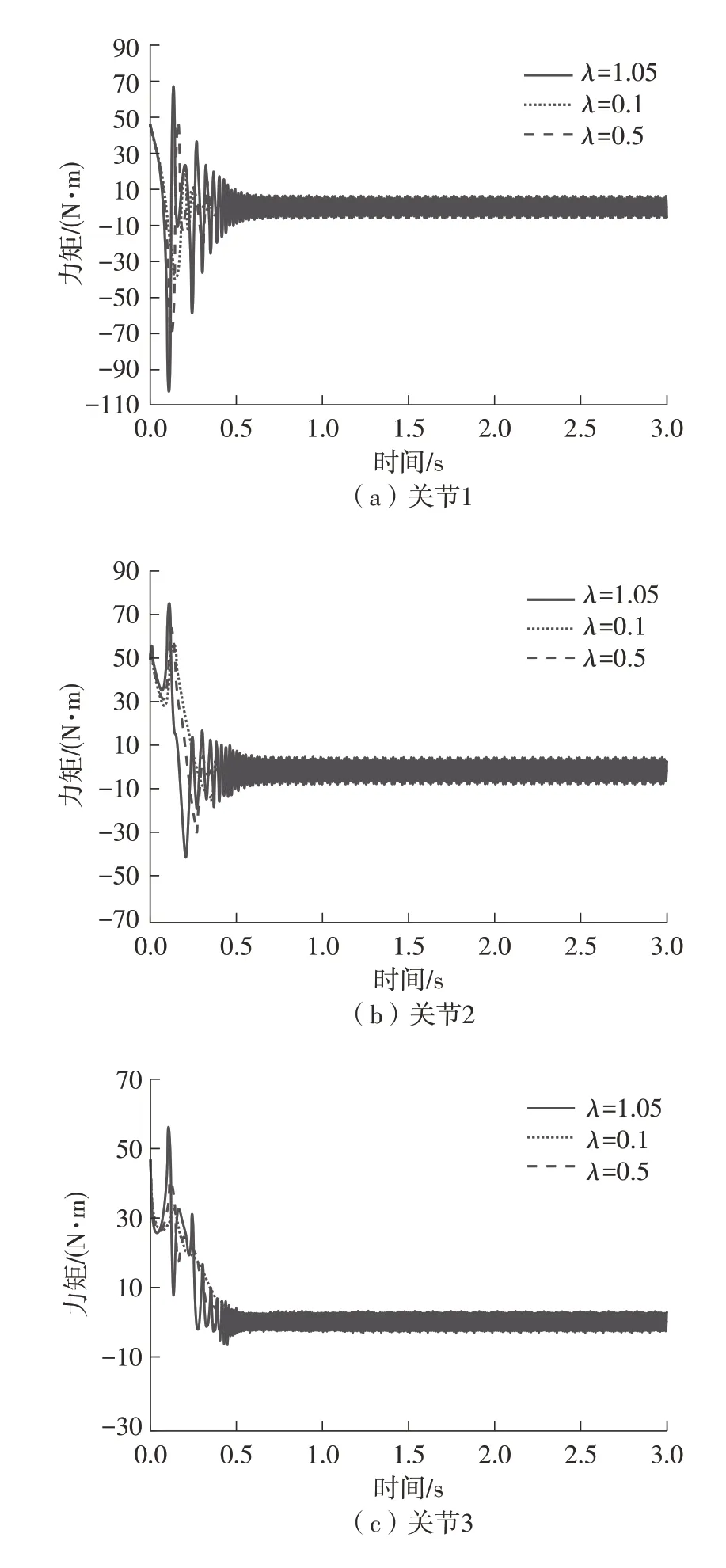
图12 不同λ时OFPD+S控制的控制力矩Fig.12 Input torques of OFPD+S control with different λ

由上述仿真结果可以得出：所提出的OFPD+S控制很好地解决了仅基于关节位置测量的多轴机器人系统输出反馈有限时间同步位置控制问题。相比于不含同步项的OPD+［6］渐近稳定控制、不含同步项的有限时间OFPD+［19］控制和渐近稳定OPD+S［27］同步控制，获得了更快的瞬态响应速度和稳态精度以及更优的同步效果。

4 结语

本文提出了多轴机器人系统的非线性PD+输出反馈有限时间同步位置控制策略，并应用Lyapunov稳定性理论和几何齐次性技术证明了闭环系统的全局有限时间稳定性。数值仿真结果表明了所提出的控制算法具有更优的收敛速度和控制精度以及较好的同步效果，从而提高了系统的整体性能。所提出的控制器不仅保证了多轴机器人系统的输出反馈全局有限时间稳定同步控制，同时也为一大类非线性二阶系统的输出反馈有限时间同步位置镇定提供了一种有效的替代方法。本文的研究方法未考虑非线性摩擦的影响，今后将致力于含摩擦的机器人系统的输出反馈位置控制技术的研究。