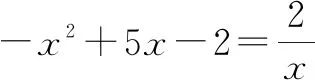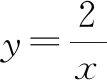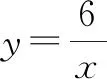快速解答中考数学选择题“六法”
尚卫成
⦿湖北省随州市广水市永阳学校
数学选择题具有“知识覆盖面广、选项设置灵活、答案唯一、答卷方式简便、评分客观公正”等诸多优点,因而深受命题人的青睐,成为各地数学中考每年的必考题型之一,且分值较高(约占总分值的20%~40%),在中考中占有十分重要的地位[1].
选择题既要考查考生对数学基本概念、定理和性质等基础知识的理解,又要考查考生对题目中所涉及的基本运算法则以及数学公式掌握的熟练程度.但是由于选择题不同于解答题,它不需要解答过程,因此解答选择题关键要做到“正确、迅速”[2].“正确”是解题的根本,而“迅速”是解题的要求,在分秒必争的考场上,面对一道分值只有几分的选择题,不可能像对待解答题那样冥思苦想耗上十几分钟,那样会得不偿失.要做到“正确、快速”地答题,就有必要学习和掌握选择题答题“六法”的技巧.
1 直接法
对于一些不用过多思考就能直接得出结论的比较简单的题目,可以从题设条件出发,利用公式、定理、定义、性质等知识,通过变形、推理、运算等,直接得到结果.

A.-6 B.6 C.-5 D.5

故答案为选项A.
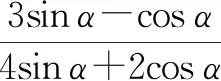
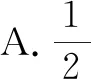
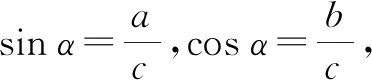
由tanα=2,知cosα≠0.
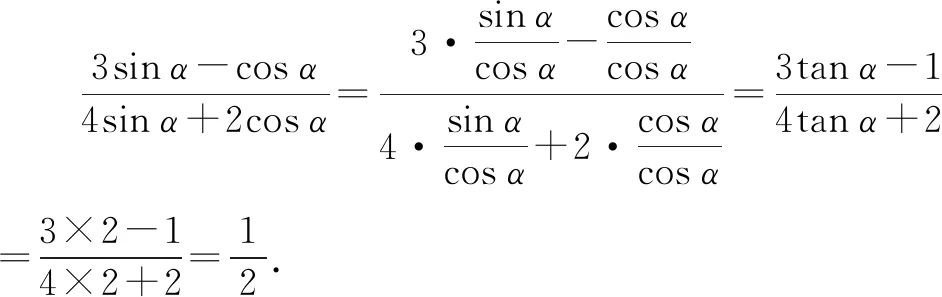
故答案为选项A.
方法与技巧:例1把函数图象经过的点的坐标直接代入解析式,求出k的值;例2利用分式的基本性质,将分子、分母同时除以cosα(cosα≠0),原式恒等变形后,再代入tanα=2求解.
2 验证法
与直接法相似,验证法是直接将各选择项中的结论代入题设条件进行检验,从而选出符合题意的答案.
例3设a>0,b>0,则下列运算错误的是( ).



故答案为选项B.
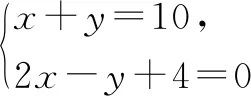


故答案为选项A.
方法与技巧:例3选取最简单的a=1,b=1,分别将它们代入选项进行检验、排除;例4将选项给出的方程组的解依次代入方程组进行验证,看是否能使方程左右两边的值相等.
3 排除法
有些选择题,一时不容易找到符合条件的选项,对此可以尝试将所有不符合条件的选项排除掉,剩下的就是正确的选项.
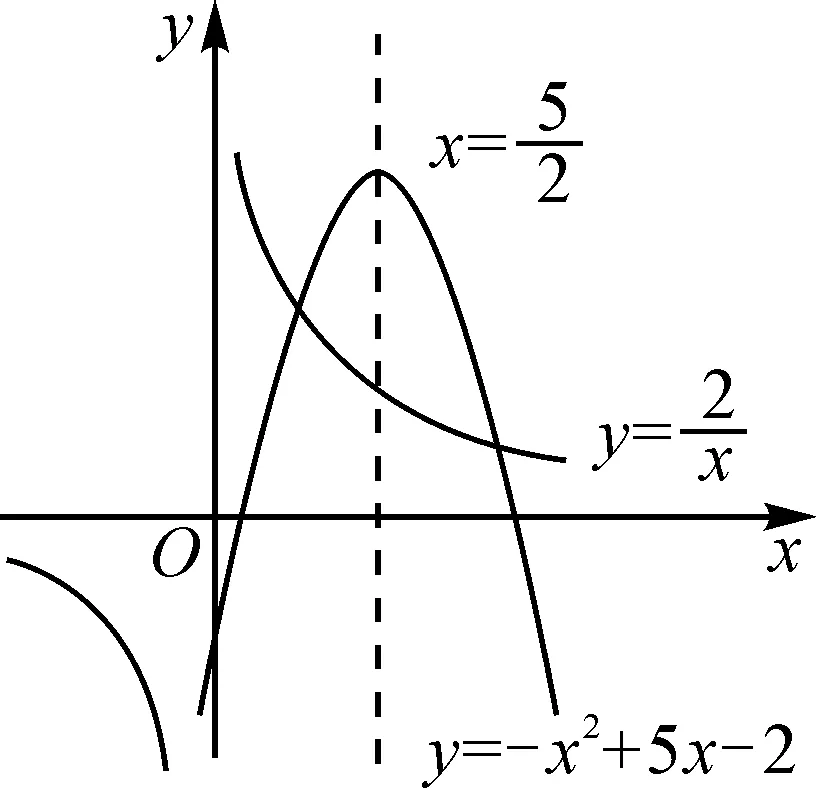
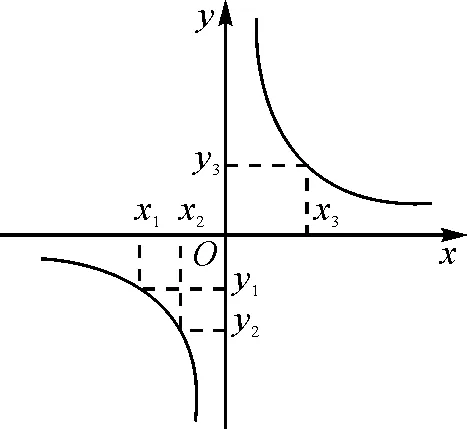
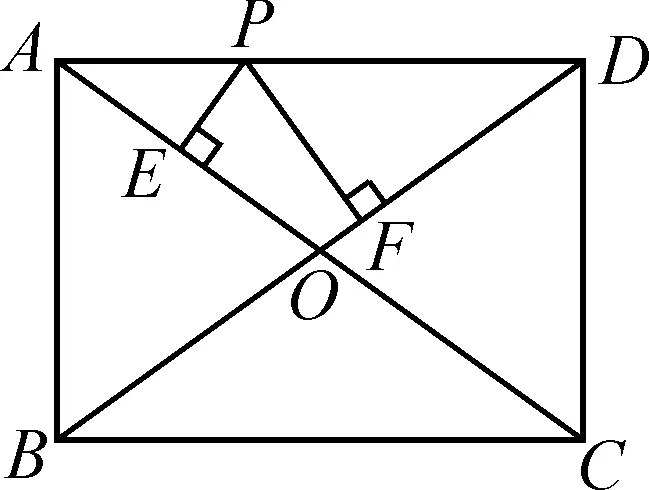
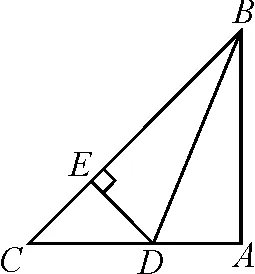
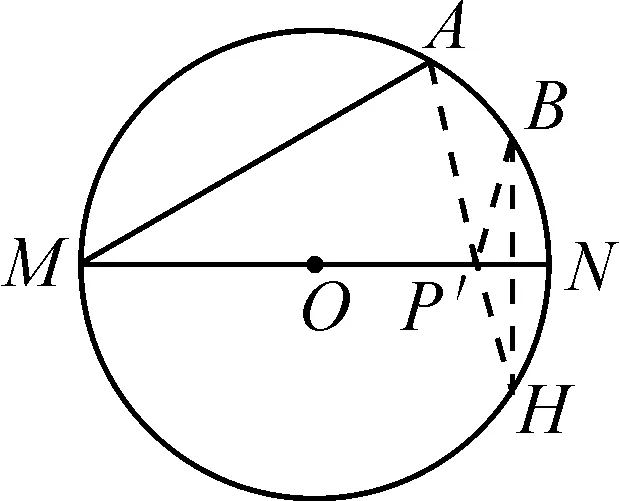
例5已知a,b为实数,则下列不等式组的解集可以为-2 故答案为选项D. A.a∶b=m∶nB.a∶m=b∶n C.a∶m=n∶bD.a∶n=b∶m 解:由比例的性质可知,A选项中,由a∶b=m∶n得bm=an,与条件不符合,排除选项A;B选项中,由a∶m=b∶n得bm=an,与条件不符合,排除选项B;D选项中,由a∶n=b∶m得bn=am,与条件不符合,排除选项D;因此剩下C选项正确. 故答案为选项C. 当选择题的结论唯一或者答案是一个定值,而已知条件中含有某些不确定的量时,可以对题中变化的不定量选取一些符合条件的特殊值或图形的特殊位置(或特殊点)进行处理,从而得出结论.当然,要注意字母的取值或图形的特殊位置必须满足条件. A.P>QB.P=Q C.P 故答案为选项C. 例8如图1,点P是矩形ABCD的边AD上的一个动点,矩形的两条边AB,BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是( ). 图1 故答案为选项A. 方法与技巧:例7采用的是取特殊值法,在考虑m取值范围的情况下,根据分母相同的特征,把m=15代入原式,通过对比结果来判断P,Q的大小关系;例8采用了特殊位置法,利用动点P与点A重合,通过添加辅助线,将点P到矩形两条对角线AC和BD的距离之和PE+PF转化为△ABD斜边BD上的高,再根据等面积法求出高. 等价转化法就是在保证前因后果具备充要条件的前提下,把一些不常见、不熟悉、较复杂的问题转化为熟悉的、规范的、简单的问题来解决. 例9如图2,已知△ABC是等腰直角三角形,∠A=90°,BD是∠ABC的平分线,DE⊥BC,垂足为E.如果BC=10 cm,那么△DEC的周长为( )cm. 图2 A.14 B.12 C.10 D.8 解:因为△ABC是等腰直角三角形,所以AC=AB.因为BD平分∠ABC,所以DE=AD,BE=AB.故△DEC周长=CE+DE+CD=CE+AD+CD=CE+AC=CE+AB=CE+BE=BC=10 cm. 故答案为选项C. 例10如图3,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为弧AN的中点,P是直径MN上的一个动点,则PA+PB的最小值为( ). 图3 图4 故答案为选项B. 方法与技巧:例9是把求周长的问题等价转化为求线段长度的问题,首先根据题中的已知条件,得到相等线段,再将△DEC的周长转化为线段BC的长;例10是将求PA+PB的最小值问题等价转化为求两点之间线段最短的问题. 判断方程根的个数时,可以采用构造函数法,将方程根的个数问题转化为函数图象交点个数的问题,通过观察函数的图象即可作出正确的判断. A.3 B.2 C.1 D.0 图5 故答案为选项B. A.y1 C.y3 解:观察图6,因为x1 图6 故答案为选项B. 方法与技巧:例11是一个分式方程,如果去分母得到的将是一个一元三次方程,超出了初中学习的范围;但如果把方程的左边看成一个二次函数,右边看成一个反比例函数,再分别画出这两个函数的图象,那么根据图象就可以看出,这两个函数在第一和第四象限的交点的个数就是原方程正根的个数.从函数的图象可以看出,两个函数的图象在第一象限有两个交点,在第四象限没有交点,所以可以断定方程有两个正根.例12是画出反比例函数的图象,直接通过观察图象即可得出正确答案. 综上所述,解答选择题的关键是要抓住一个“选”字,尽量减少解题书写过程,对待选择题要“小题小做”,不能像对待解答题那样“小题大做”;要掌握解题方法与技巧,依据题目的特点,做到快速、灵活、高效、巧解.
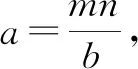
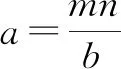
4 特殊值或特殊位置法
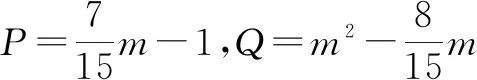
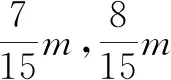
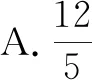
5 等价转化法

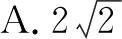
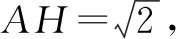
6 作图观察法