浅探“等效电源”的理解和应用

■河南省信阳高级中学 左刚武

等效替代是在保证某种效果相同的前提下,将实际的、复杂的物理问题和物理过程转化为简单的、易于研究的物理问题和物理过程的方法。在学习电路这部分知识时,若能巧妙运用等效电源法进行分析与求解,则可以达到事半功倍的效果。

一、何为“等效电源”

1.定值电阻与电源相串联的等效。

在电路中,当电源与一个定值电阻串联时,我们可以将电源与定值电阻视为一个整体,等效为一个新的电源,如图1所示。

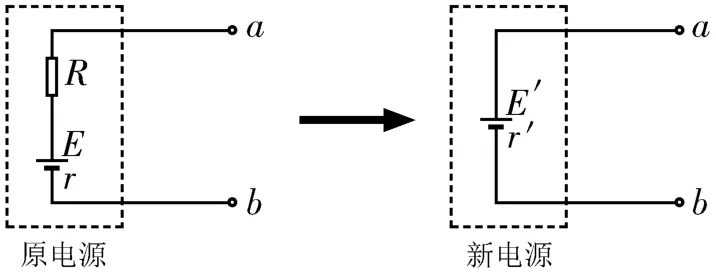
图1

对于原电源,当a、b两点间外电路断路时,a、b两点间电压等于新电源的电动势,则E'=E,原电源与定值电阻串联,则r'=r+R。

2.定值电阻与电源相并联的等效。

在电路中,当电源与一个定值电阻并联时,我们可以将电源与定值电阻视为一个整体,等效为一个新的电源,如图2所示。

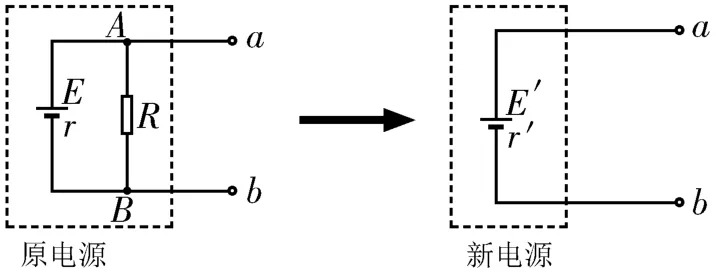
图2

对于原电源,当a、b两点间外电路断路时,a、b两点间电压(A、B两点间电压)等于新电源的电动势,则E'=Uab=UAB;当a、b两点间外电路断路时,原电源直接对定值电阻R供电,则,即。新电源的等效内阻等于原电源内阻与定值电阻并联后的总电阻,则。

以上两种情况是关于等效电源的常见表述。为了解上述表述的本质,下面进行追根溯源,体会等效电源“等效”的根源所在。

设通过a、b两点间外电路的电流为I,a、b两点间的电压为U。

定值电阻与电源相串联的等效之根源:根据闭合电路欧姆定律可得,原电源满足U=E-I(R+r),新电源满足U=E'-Ir',将U、I进行等效对比得E'=E,r'=R+r。

定值电阻与电源相并联的等效之根源:根据闭合电路欧姆定律可得,原电源满足,整理得,新电源满足U=E'-r'I,将U、I进行等效对比得。

为了研究其他的复杂电路是否也具有这样的“根”,下面以一个混联电路为例进行分析。

如图3所示,将电源与混联的电阻R1和R2视为一个整体,根据闭合电路欧姆定律可得,原电源满足,整理得,新电源满足U=E'-r'I,将U、I进行等效对比得。显然,在这个混联电路中,“等效”关系依然成立。

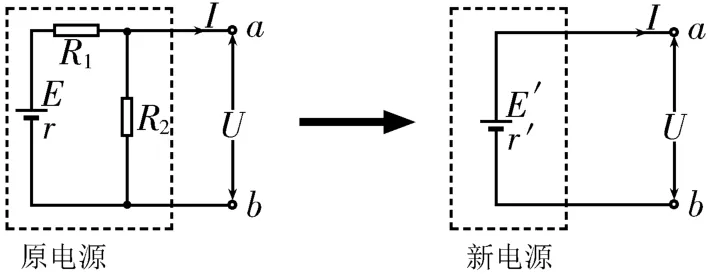
图3

二、“等效电源”在实际电路中的应用

1.巧选对象解决U与I变量的问题。

例1如图4所示,R1、R2、R3都是阻值为R0的定值电阻,R是滑动变阻器,电源电动势为E,内阻为r。闭合开关S,当滑动变阻器的滑片P由图示位置向右缓慢滑动时,ΔU1、ΔU2分别表示理想电压表V1、V2示数的变化量,ΔI表示理想电流表A 示数的变化量,则下列说法中正确的是( )。

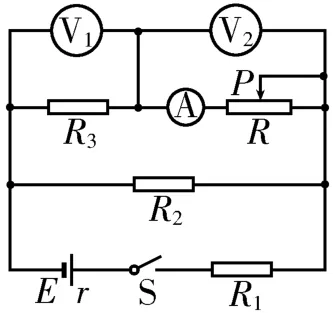
图4

解析:本题考查的是电路的动态变化这一主干知识点。求解的关键是正确选择研究对象利用对应的伏安特性曲线的斜率解决问题。在如图5 所示的电阻的伏安特性曲线中,定值电阻的阻值等于图甲中直线的斜率,即,其值是不变的,对应本题中的定值电阻不变,选项A 正确。不定值电阻的阻值等于图乙中虚线的斜率,即,其值是不断变化的。当滑片P向右滑动时,滑动变阻器接入电路的阻值变大,所以变大。将怎么变化呢? 在不定值电阻的伏安特性曲线中并不代表其阻值的大小,不能直接进行判断。若采用“等效”思想,将电路中的R1、R2、R3内化到电源里面去,问题就“水落石出”了。经过等效变换,相当于一个电动势为,内阻为的电源对滑动变阻器R供电,这样就表示“等效电源”的内阻,在滑动变阻器接入电路的阻值变化的过程中,保持不变,选项B 错误,C 正确。同理,选项D也正确。

图5

答案:ACD

2.确定非线性元件的工作状态。

例2在如图6所示的电路中,电源电动势E=3 V,内阻r=5 Ω,定值电阻R=5 Ω,在电路中的黑箱里放置有一个未知的电子元件。为研究该元件的电阻特性,测得其两端电压与通过电流的关系如图7所示。求该电子元件在电路中消耗的电功率。

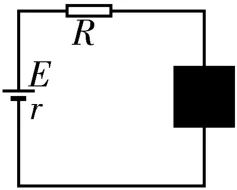
图6

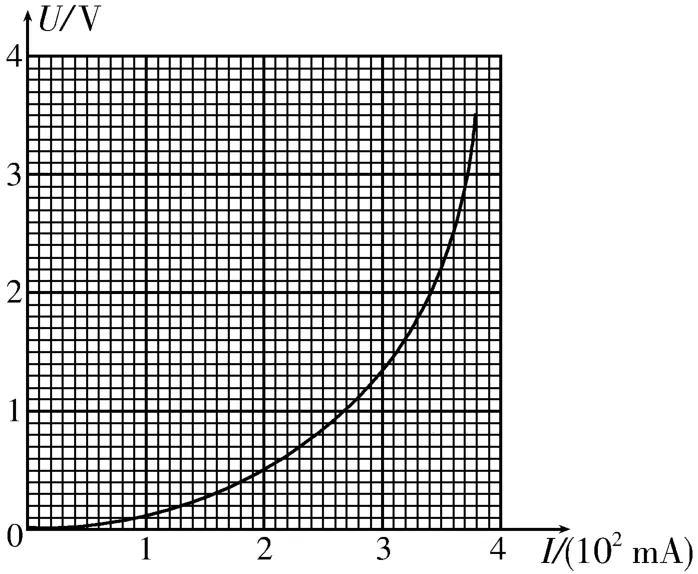
图7

解析:根据电子元件的U-I图像可知,该元件为非线性元件,按常规解法不能确定该元件的工作状态。将电源与定值电阻R视为一个整体,等效为一个新电源,令新电源的电动势为E1,内阻为r1,则E1=E=3 V,r1=R+r=10 Ω。对于新电源,设其路端电压为U,则U=E1-Ir1,即U=3-10I。在如图7所示的U-I图像中作出新电源的路端电压U与干路电流I的关系图像,如图8所示,则两图像的交点即为该元件的工作状态。读图得交点坐标为U1=0.7 V,I1=2.3×102mA,则该电子元件在电路中消耗的电功率P=U1I1=0.161 W。

图8

3.确定可变电阻消耗电功率的变化情况。

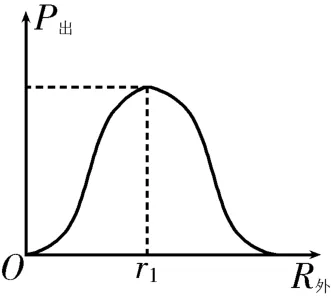
例3如图9 所示,已知电源电动势E=6 V,内阻r=1 Ω,定值电阻R0=5 Ω,滑动变阻器R的最大阻值Rmax=4 Ω,当滑片P向右滑动时,判断滑动变阻器消耗的电功率如何变化,并求其消耗电功率的最大值Pmax。

图9

解析:将电源和定值电阻R0视为一个整体,等效为一个新电源,令新电源电动势为E1,内阻为r1,则E1=E=6 V,r1=R0+r=6 Ω,滑动变阻器为新电源的外电阻,其消耗的电功率即为新电源的输出功率。新电源输出功率与外电阻的关系满足,新电源的输出功率随外电阻的变化关系如图10所示。当R外

图10

4.分析电学实验中的系统误差。

在测量电池电动势和内阻的实验中,系统误差分析是一个难点。利用等效电源法进行分析,该问题将会迎刃而解。

(1)电流表外接法的系统误差分析。

实验电路如图11所示,令电源电动势为E,内阻为r,该实验的实验原理为U=E-Ir,引起系统误差的原因在于电压表的分流,将电压表与电源视为一个整体,等效为一个新电源,令新电源电动势为E1,内阻为r1,则,即E测=E1

图11

(2)电流表内接法的系统误差分析。

实验电路如图12所示,令电源电动势为E,内阻为r,该实验引起系统误差的原因在于电流表的分压,将电流表与电源视为一个整体,等效为一个新电源,令新电源电动势为E2,内阻为r2,则E2=E,r2=r+RA,即E测=E2=E真,r测=r2>r真。

图12

总之,在高中物理的学习过程中,等效思想的使用范围相当广泛。高中阶段我们为了“化繁为简”,提高解题效率,会慢慢养成“记忆”二级结论的习惯,不过,牢记物理学习的初心——理解、分析、推理→问题解决→能力提升,方能圆大物之梦、悟大物之美。