浅探安培力的理解和应用

■山西省太原市第五职业中学校 赵红梅

安培力是指通电导线在磁场中受到的力,是洛伦兹力(运动电荷在磁场中受到的力)的宏观表现。安培力既可以不做功,也可以做正功(电动机原理),还可以做负功(发电机原理)。理解安培力需从理解安培力的方向和大小入手,求解涉及安培力的问题需要重点关注受力分析。下面举例说明,供同学们参考。

一、安培力的理解

1.对安培力方向的理解。

判断安培力的方向一般采用左手定则,即伸开左手,使拇指与其余四个手指垂直,并且都与手掌在同一个平面内;让磁感线从掌心垂直进入,并使四指指向电流的方向,这时拇指所指的方向就是通电导线在磁场中所受安培力的方向。在使用左手定则判断安培力的方向时,需要明确磁感应强度B、电流I、安培力F与手掌、四指、拇指的一一对应关系,以及三者之间的空间关系。为了方便理解和记忆,可将左手定则用如图1 所示的立体几何展示出来。

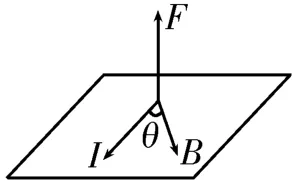
图1

注意:在任何情况下,总有F⊥I,F⊥B,即两垂直关系是永远成立的;I和B可以成任意夹角θ,不一定是垂直关系。

例1如图2 所示,通电导体受到的安培力F的方向垂直于纸面,电流的方向分别如图中I或I'所示,磁感应强度的方向分别如图中B或B'所示。下列关于安培力、电流、磁感应强度三者方向的说法中正确的是( )。

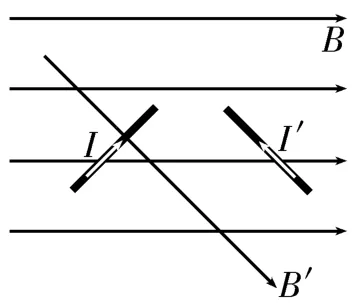
图2

A.若已知电流的方向为I,磁感应强度的方向为B,则安培力F的方向一定垂直于纸面向内

B.若已知电流的方向为I',磁感应强度的方向为B,则安培力F的方向一定垂直于纸面向内

C.若已知安培力F的方向垂直于纸面向内,磁感应强度的方向为B,则电流的方向一定为I

D.若已知安培力F的方向垂直于纸面向内,电流的方向为I,则磁感应强度的方向只可能为B或B'

解析:已知电流的方向为I,磁感应强度的方向为B,则根据左手定则可知,安培力F的方向一定垂直于纸面向内,即安培力F的方向垂直于电流I与磁感应强度B所决定的平面,选项A 正确。已知电流的方向为I',磁感应强度的方向为B,则根据左手定则可知,安培力F的方向一定垂直于纸面向内,选项B 正确。已知安培力F的方向垂直于纸面向内,磁感应强度的方向为B,则电流的方向可能为I,也可能为I',还可能是其他方向,即仅知道安培力和磁感应强度的方向,不能确定电流的方向,选项C 错误。已知安培力F的方向垂直于纸面向内,电流的方向为I,则磁感应强度的方向可能为B,也可能为B',还可能是其他方向,即仅知道安培力和电流的方向,不能确定磁感应强度的方向,选项D 错误。

答案:AB

2.对安培力大小的理解。

通电导线在磁场中受到的安培力的计算公式为F=BIlsinθ,其中θ表示I和B之间的夹角,当θ=0 或180°,即电流与磁感线平行时,安培力等于0;当θ=90°,即B、I、F成三垂直关系时,安培力取最大值BIl。

注意:安培力大小的计算公式F=BIlsin

θ只适用于匀强磁场,对于非匀强磁场,要想利用这个公式求解,则需l足够短,近似认为l所在处的磁场为匀强磁场;l是指位于磁场中通电直导线的长度,若位于磁场中的导线是弯曲的,则代入公式计算的应是其有效长度,即弯曲导线两端点连线的长度。

例2空间存在磁感应强度B=0.5 T 的匀强磁场,将一根长度l=0.2 m,通有电流I=3 A 的直导线放置在此匀强磁场中,则导线受到的安培力大小可能是( )。

A.0 B.0.1 N

C.0.2 N D.0.4 N

解析:根据安培力大小的计算公式F=BIlsin

θ可知,当磁感应强度B与电流I的方向垂直,即θ=90°时,安培力取最大值,且Fmax=BIl=0.3 N;当磁感应强度B与电流I的方向平行,即θ=0 或180°时,安培力取最小值,且Fmin=0。因此,导线受到的安培力大小在0到0.3 N 之间取值。

答案:ABC

二、涉及安培力问题的求解策略

1.涉及安培力平衡问题的求解策略。

涉及安培力的平衡问题的本质是力学平衡,只是在进行受力分析时需要注意安培力的大小和方向。涉及安培力的问题往往是三维立体空间内的问题,为了便于分析与求解,应先将“立体图”转化为“平面图”,再找出I、B方向之间的关系,根据左手定则判断安培力的方向,最后根据平衡条件列式求解。

例3如图3所示,在倾角为θ的绝缘光滑斜面上,放置一通有电流I、质量为m、长度为L的导体棒。

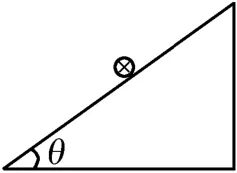
图3

(1)欲使导体棒静止在斜面上,求外加匀强磁场的磁感应强度B的最小值和方向。

(2)欲使导体棒静止在斜面上且对斜面无压力,求外加匀强磁场的磁感应强度B的大小和方向。

(3)分析导体棒有可能静止在斜面上且B⊥I情况下,外加匀强磁场的方向范围。

解析:(1)选导体棒为研究对象,进行受力分析,导体棒受重力mg、斜面支持力N、安培力F三个力作用处于平衡状态。根据平衡条件可知,当安培力F等于重力mg沿斜面方向的分力mgsinθ,且磁感应强度B的方向与电流I的方向垂直时,磁感应强度B的值最小。根据BIL=mgsinθ,解得。根据左手定则可知,磁感应强度B的方向垂直于斜面向上。

(2)欲使导体棒静止在斜面上且对斜面无压力,则导体棒只受重力mg和安培力F两个力作用处于平衡状态,根据mg=BIL,解得。根据左手定则可知,磁感应强度B的方向水平向左。

(3)建立如图4 所示的平面直角坐标系Oxy,要使导体棒静止在斜面上且B⊥I,则安培力的方向需限定在图中F1、F2之间,且包括F2的方向,而不包括F1的方向。根据左手定则可知,外加匀强磁场的磁感应强度B需限定在图中B1、B2之间,且包括B2的方向,而不包括B1的方向,因此外加匀强磁场的方向与x轴正方向之间的夹角α应满足θ<α≤π。

图4

2.涉及安培力加速问题的求解策略。

涉及安培力的加速问题的本质是力学加速,将“立体图”转化为“平面图”后,正确进行受力分析,根据牛顿第二定律列式求解即可。

例4如图5所示,一绝缘光滑斜面体固定在匀强磁场中,磁感应强度为B,方向垂直于斜面向上,通有电流I的导体棒静止在斜面上。若保持磁场和电流的方向不变,将磁感应强度大小改为2B,将电流大小改为,则导体棒( )。

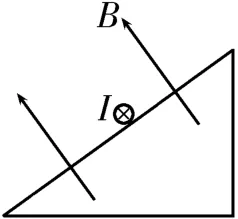
图5

A.仍静止在斜面上

B.沿斜面匀速上滑

C.沿斜面加速上滑

D.沿斜面加速下滑

解析:当磁感应强度大小为B,电流大小为I时,导体棒受到竖直向下的重力、垂直于斜面向上的支持力和沿斜面向上的安培力三个力作用处于平衡状态。设导体棒的长度为L,则安培力的大小F=BIL。设导体棒的质量为m,斜面的倾角为θ,根据平衡条件得F=mgsinθ。当磁感应强度大小变为2B,电流大小变为时,安培力大小变为,因为F'

答案:D

跟踪训练

1.如图6所示,平面梯形框架abcd由粗细均匀的电阻丝折成,已知ab=ad=bc=L,腰ad、bc均与底边dc成60°角,框架处于磁感应强度为B的匀强磁场中,且磁场与框架平面垂直,长度为L的电阻丝的电阻为r。

图6

(1)若将框架的a、b两点与电动势为E,内阻为r的电源相连,求通入沿顺时针方向的电流后整个框架受到的安培力。

(2)若将电动势为E,内阻为r的电源直接接在框架的ab边上,求通入沿顺时针方向的电流后整个框架受到的安培力。

2.如图7所示,静止在光滑斜面上的条形磁铁上端与一根轻弹簧相连,此时磁铁对斜面的压力为F1。现将一根直导线沿着与磁铁垂直的方向,水平放置在磁铁中点正上方的A处,当给导线通电时,发现弹簧下端上移了一点,若稳定后磁铁对斜面的压力为F2,则F1与F2的大小关系如何? 导线中电流的方向怎样?

图7

3.如图8所示,PQ、MN两平行导轨固定在同一水平面上,并处在竖直向上的匀强磁场中。一根质量m=2 kg,有效长度L=1 m 的金属棒放置在导轨上,始终与导轨接触良好。当金属棒中通入电流I1=5 A 时,金属棒做匀速直线运动;当金属棒中通入电流I2=8 A 时,金属棒获得加速度a=1 m/s2。求磁感应强度B。

图8

参考答案:1.(1),方向竖直向上;(2)F=0。

2.若导线中电流的方向向内,则F1F2。