高三物理一轮复习阶段检测B卷(必修第三册和选择性必修第二册)参考答案与提示
1.C 提示:与电源断开,电容器所带电荷量Q不变,插入金属板C之前,电容器两极板间场强,又有解得。插入金属板C之后,静电平衡状态下,插入的金属板C内部场强为0。金属板C两侧面感应出等量异种电荷,这时电容器等效于两个新电容器串联。设电容器两极板与插入的金属板间隙中的场强为E,根据,解得。可见E=E0,因此带电小球的受力情况不变,悬挂带电小球的细线的倾角θ不变。
2.B
3.B 提示:橡胶板带负电,铝板靠近后,铝板的下表面带正电,上表面带负电,当其下表面与接地铁钉接触后,上表面的负电荷会流向大地,只有下表面带正电,选项A、C、D错误。上抬铝板过程中,下表面的正电荷减小,上表面正电荷增加。纸屑因为与铝板带同种电荷(正电荷)而不断飞散,选项B正确。
4.D 提示:金属球静电平衡,则E=0,且φ=500 kV,选项A、B 正确。加速罩通过电阻和质子束放电,通过电阻放电的电流,需要供给加速罩的总电流I=IR+Ip=75 μA,这个电流被喷到橡胶带上,根据I=σDv,解得σ=37.5 μC/m2,选项C 正确。质子束在加速过程中,根据动能定理得,在磁场中有,质子在磁场中的运动轨迹如图1所示,根据几何关系得,联立以上各式解得B=0.58 T,选项D 错误。
5.CD 提示:小球在过程1中经过A点时受到的库仑力大小,选项A 错误。在P点,根据牛顿第二定律得,解得,选项B错误。根据单摆周期公式可知,小球若做单摆运动,在过程1中从A点首次运动到B点所用的时间。但因为弧长约等于R,小球的实际运动不能视为单摆,所以小球的实际运动时间大于t,选项C正确。假设小球在过程2中受到的库仑力始终为0.5 N 不变,则mg+F=ma,解得a=20 m/s2。根据运动学公式得,解得t=0.2 s。而实际上小球受到的库仑力是逐渐减小到0.5 N 的,因此小球在过程2中的运动时间小于0.2 s,选项D 正确。
6.ACD 提示:金属棒从aa'位置运动到最低位置bb'处的过程中,水平分速度(有效切割速度)逐渐增大,根据E=BLv可知,金属棒产生的感应电动势增大,则通过电阻R的电流逐渐增大;金属棒从最低位置bb'运动到cc'处的过程中,水平分速度(有效切割速度)逐渐减小,根据E=BLv可知,金属棒产生的感应电动势减小,则通过电阻R的电流逐渐减小。因此金属棒经过最低位置bb'处时,通过电阻R的电流最大,选项A 正确。根据右手定则可知,金属棒经过最低位置bb'处时,通过金属棒的电流方向为b→b',选项B错误。整个过程中,通过电阻R的电荷量,选项C 正确。金属棒做匀速圆周运动,切割磁感线的有效速度v=v0cosθ=v0cosωt,其中θ是金属棒的速度与水平方向间的夹角,则金属棒产生的感应电动势E0=BLv0cosωt,则回路中产生正弦式交变电流,可得感应电动势的有效值。根据焦耳定律可知,电阻R上产生的热量,选项D正确。
7.AD 提示:根据左手定则可知,电子向N侧面偏转,N表面带负电,M表面带正电,所以M表面的电势较高,选项A 正确。仅改变磁感线与霍尔元件工作面间的夹角,在垂直于工作面方向上的磁感应强度将小于原磁场磁感应强度的大小,则UH将减小,选项B 错误。根据,I=nqvS=nqvdh,解得,可见UH与宽度d无关,因此仅减小霍尔元件的厚度h,M、N两端电压UH一定增大,选项C 错误,D正确。
8.AD 提示:因为洛伦兹力不做功,粒子的动能保持不变,所以带电粒子在由中央向两端运动的过程中,平行于轴向OO'方向的速度逐渐减小,垂直于轴向OO'方向的速度会越来越大,选项A 正确,B错误。因为地球的磁场沿南北方向,粒子在南北方向上运动时,不受洛伦兹力,只不过不同纬度上空磁感应强度不同,根据“磁镜”原理可知,粒子在南北方向上来回反射时,在磁感应强度大的地方,沿磁场方向的速度减小,在磁感应强度小的地方,沿磁场方向的速度增大,选项C错误,D 正确。
9.(1)①A②R1(2)R2
10.(1)BCE(2)如图2 所示(3)4×103
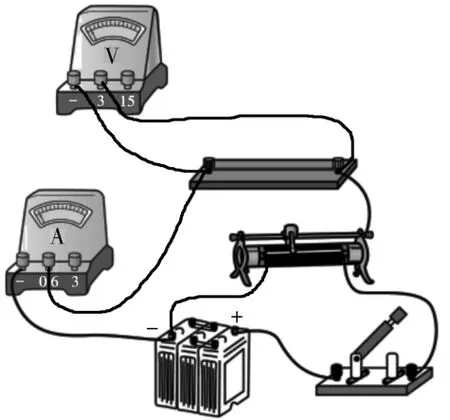
图2
11.(1)金属棒和导体框在没有进入磁场时一起做匀加速直线运动,根据动能定理得,解得。金属棒在磁场中切割磁感线产生感应电动势,根据法拉第电磁感应定律得E=BLv0,根据闭合回路欧姆定律得,则金属棒刚进入磁场时受到的安培力F安=BIL=0.18 N。(2)金属棒进入磁场以后,因为瞬间受到安培力的作用,根据楞次定律可知,金属棒受到的安培力沿斜面向上,之后金属棒相对导体框向上运动,因此金属棒受到导体框给的沿斜面向下的滑动摩擦力,匀速运动时有mgsinα+μmgcosα=F安,此时导体框向下做匀加速运动,根据牛顿第二定律得Mgsinα-μmgcosα=Ma。设磁场区域的宽度为x,则金属棒在磁场中运动的时间。当金属棒刚好离开磁场区域时,导体框的速度v1=v0+at,则导体框的位移,因此导体框和金属棒的相对位移。当金属棒离开磁场时导体框的上端EF刚好进入磁场,则s0-Δx=x,导体框进入磁场时做匀速运动,产生的感应电动势E1=BLv1,感应电流,导体框受到向上的安培力和滑动摩擦力,根据平衡条件得Mgsinα=μmgcosα+BI1L。联立以上各式解得x=0.3 m,a=5 m/s2,m=0.02 kg,。(3)金属棒出磁场以后,速度小于导体框的速度,因此受到向下的滑动摩擦力,做加速运动,则mgsinα+μmgcosα=ma1,金属棒向下加速,导体框匀速,当二者达共速时导体框不再匀速,则v1=v0+a1t1,导体框匀速运动的距离x2=v1t1,解得。(4)导体框在t2=0.009 s时间内,根据动量定理得,其中,解得导体框出磁场时的速度v=2.52 m/s。对导体框应用动能定理得,解得W安=0.006 3 J,即金属棒中产生的热量Q=0.006 3 J。
12.(1)根据x-t图像可得,3.2 s后金属棒达到了最大速度,最大速度。金属棒达到最大速度时受到的安培力等于重力,则mg=BIL,其中,联立以上各式解得B=0.1 T。(2)方法一:金属棒在开始运动的3.2 s 时间内下降的距离x1=17.5 m,通过电阻R的电荷量,解得q=2.5 C。方法二:对金属棒应用动量定理得(mg-BIL)Δt=mΔv,又有q=IΔt,解得q=2.5 C。(3)根据能量守恒定律可知,金属棒在开始运动的3.2 s时间内减小的重力势能转化为金属棒的动能和电路的内能。设电路中产生的总焦耳热为Q总,根据能量守恒定律得,电阻R上产生的热量,解得QR=0.86 J。
13.(1)如图3 所示,带电粒子速度最小时有r1=R,,解得。如图4 所示,带电粒子速度最大时有,解得。因此带电粒子的速度范围是。(2)带电粒子在磁场中运动时有,,解得带电粒子在磁场中运动的周期。带电粒子在磁场中运动的周期相同,从磁场边缘运动到行星赤道平面偏转的角度越小,运动的时间越小。根据几何关系可得,磁场边界和赤道上点连线越短,带电粒子在磁场中的运动轨迹所对的圆心角越大,偏转角度越小。带电粒子的运动轨迹对应的最短弦长为2R,最大轨迹半径为2R,如图5所示,此时带电粒子从磁场边缘运动到行星赤道平面的时间最短。带电粒子的运动轨迹所对的圆心角,带电粒子从磁场边缘运动到行星赤道平面的最短时间。(3)如图6所示,带电粒子以最大速度运动的轨迹与赤道上半圆弧相切点为辐射盲区的上边界点,从A点射入的带电粒子恰好能达到赤道线下半圆弧的最右侧,则从A点射入的带电粒子以最大速度运动的轨迹与赤道线的交点为辐射盲区的下边界点。根据几何关系可知,△COO'为等腰三角形,CO=OO'=3R,CO'=2R,所以。CO'与AB平行,因此赤道上辐射盲区对应的圆心角等于θ,其正弦值。

图3
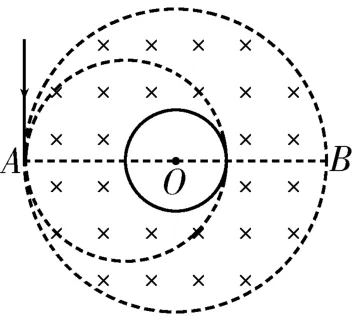
图4
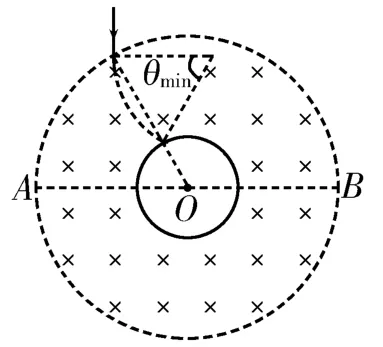
图5
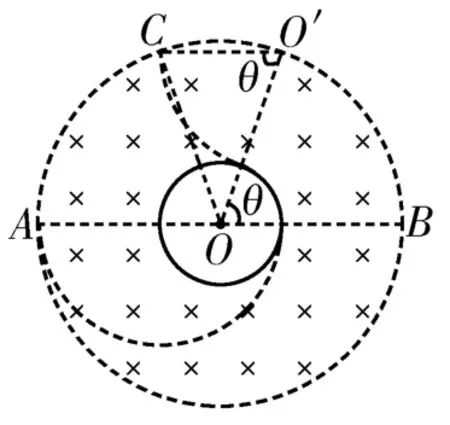
图6
——以2023年高考湖南卷物理第14题为例

