基于BP神经网络的二级公路线形事故风险判别

杨永红，王醇杨朝，陈劲宇，

1）华南理工大学土木与交通学院，广东广州 510641；2）长沙理工大学公路工程教育部重点实验室，湖南长沙 410114；3）广东省隧道工程安全与应急保障技术及装备企业重点实验室，广东广州 510550；4）广东华路交通科技有限公司，广东广州 510420

道路交通事故影响人们的生命安全.研究表明，不良的道路条件在交通事故的致因中占比70%，道路线形与交通安全密切相关［1-2］.为了提高道路安全品质，减少道路交通事故的发生，有必要对造成事故的原因以及导致事故的路段进行深入剖析以提高道路运行安全.

寇敏等［3］提出不协调的道路线形、危险的道路条件和驾驶人操作失误等原因往往会导致交通事故发生.林志英［4］提出如是单纯的由于驾驶员个人失误因素通常不会导致严重的交通事故，往往是由于不协调的道路线形、危险的道路条件所导致.PARK 等［5］研究高速公路上下坡路段纵坡与交通事故之间的关系，结果表明在上坡时坡度增大事故率下降，在下坡时坡度增大事故率上升.FU 等［6］通过研究表明道路纵断面线形坡度和平曲线半径大小与事故率之间呈现指数相关关系.CIOCA等［7］通过研究2012—2016 年间罗马尼亚的事故数据发现，考虑道路环境时，弯道设置不合理是造成事故的最大因素.陈昭明等［8］构建了基于负二项分布的事故分析模型，研究结果表明急弯、陡坡及其组合线形均会对交通安全产生不利影响.郭应时等［9］分析山区公路事故率与道路平面线形之间的关系，发现单一曲线内的事故不仅受该平面线形的影响，且受到相邻路段特别是事故发生前路段的线形因素的影响.李艳等［10］分析道路几何设计、交通运行与单车和多车两类事故类型事故数之间的关系，表明路段长度、平曲线曲率、车道数及中央分隔带的宽度均对两类事故产生影响.王华荣等［11］通过研究山区双车道公路追尾事故分布规律与道路线形的关系，表明山区双车道公路上追尾事故与纵断面线形要素相关，尤其是累计坡长对追尾事故影响显著.温惠英等［12］通过对山区公路事故黑点的鉴别，根据计算结果可知，道路线形不良是山区公路事故黑点的主要成因.涂圣文等［13］对双车道公路考虑平纵组合线形的事故预测模型进行线形安全分析，结果表明平曲线与变坡点两侧纵坡坡度方向不一致的凹曲线组合时，事故发生率最高.苏晓智等［14］对高速公路纵面线形事故风险概率进行研究分析，指出竖曲线半径大小应与直坡长度大小相对应，同取较大或较小值.上述研究主要是通过分析道路事故率与各线形指标的关系得出不利线形与交通事故有明显相关性.

孟祥海等［15］针对道路事故率与线形指标、交通量之间的关系建立神经网络事故预测模型，验证了神经网络模型在交通安全机理上的可靠性.符锌砂等［16］建立反向传播（back propagation，BP）神经网络，以事故、线形和经济损失等指标作为输入变量对事故黑点治理紧迫性进行排序研究.陈君等［17］对交通事故调查分析的基础上建立相应评价指标，构建BP 神经网络模型进行交通安全评价，结果表明该评价模型精确可靠.可见，通过神经网络模型分析事故与线形之间的关系已有理论基础，并且具有一定的可靠性.

李相勇等［18］建立基于BP 神经网络的道路交通安全综合评价模型，验证了神经网络模型的交通安全综合评价模型的合理性及有效性.郭忠印等［19］通过回归得到事故率与线形综合指标的关系，结果证明线形综合指标可作为道路安全评价的评价指标.丰明洁等［20］根据横向加速度分布特征，将平纵组合路段划分为GOOD、FAIR和POOR三个安全等级进行安全评价.由此可见，采用神经网络模型进行事故分析及安全评价具有可靠性.

以上文献通过研究事故与道路线形之间的联系，分析导致事故的线形指标，得出了个别线形指标下的事故变化情况，但对于导致事故的路段区间并未深入研究.本研究通过分析已有的道路历史交通事故数据，研究道路平纵面线形指标与事故率之间的关系，基于当量事故数构建BP神经网络模型，综合求解线形指标对事故发生影响的权重系数，探究基于道路线形及事故严重程度的事故危险区间，得到事故桩号点处的路段线形风险指数，为事故其他致因的研究提供精确道路区间参考.

1 基于事故率的风险评价等级

1.1 样本选取

CHENG 等［21-23］提出3 a 内的道路交通事故资料可用于交通繁忙的道路网的研究，正在进行道路改造或已完成道路改造的地区，最好使用3～5 a内的道路数据资料.这是因为:①能够提供较多有效数量的事故资料来获得有意义的结果；②时间跨度足够短，可以减少交通数量和道路环境的变化对结果偏差的影响；③该期间的数据有助于消除统计波动和减少回归均值效应的影响；④合理的时间跨度为前后数据比较提供了一致的统计基础.因此，本研究选取贵州省某二级公路K158+000 至K229+000 全长71 km 的道路3 a 内的事故数据为基础样本，并且整理事故所在桩号范围内的路段线形情况.

1.2 数据处理

本研究路段为二级公路，以《公路工程技术标准》（JTG B01—2014）［24］中当二级公路设计速度为60 km/h 时对应的停车视距75 m 为基本事故危险路段，分析道路线形指标.剔除与道路线形无关数据，以发生事故的路段各指标最小值开始统计，并整理各线形指标取值下的事故数量及路段占比情况，结果可扫描论文末页右下角二维码查看补充材料表S1.

1.3 数据分析

路段事故率表示各线形指标下的事故数占各路段的比值，各线形指标下的路段事故率见图1.

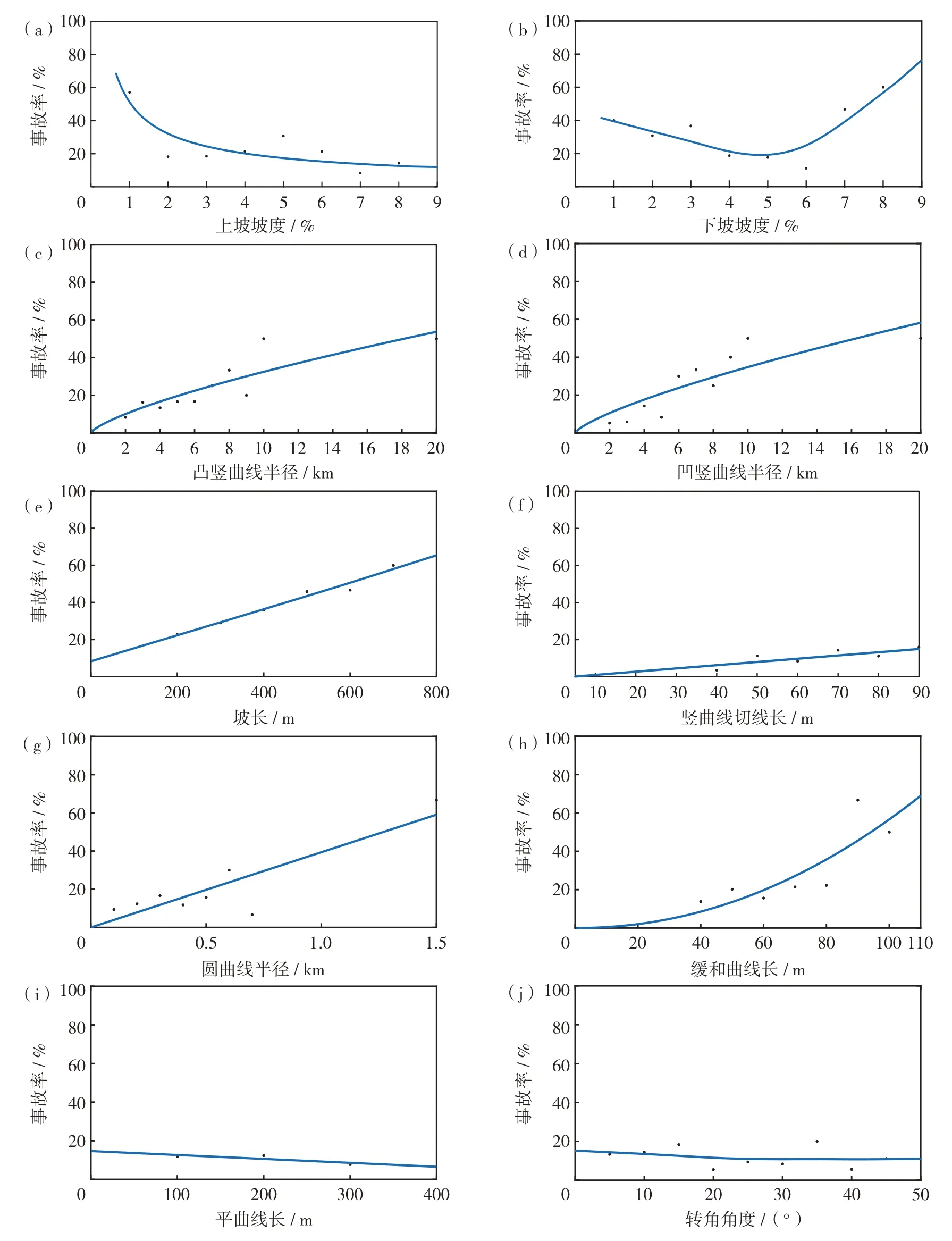
图1 （a）上坡坡度、（b）下坡坡度、（c）凸竖曲线半径、（d）凹竖曲线半径、（e）坡长、（f）竖曲线切线长、（g）圆曲线半径，（h）缓和曲线长、（i）平曲线长和（j）转角角度下的路段事故率Fig.1 (Color online) Accident rates of road section under (a) uphill gradients,(b) downhill gradients,(c) radii of crest curves,(d) radii of sag curves,(e) slope lengths,(f) vertical curve tangent lengths,(g) radii of circular curves,(h) transition curve lengths,(i) flag curve lengths,and (j) deflection angle.

由图1（a）可知，上坡时事故率随着坡度的增大而减小，当公路上坡坡度为1%～3%时具有较低的事故率，且风险评价等级较低.由图1（b）可知，下坡时当公路的坡度陡于5%时，坡度越陡事故率越高，而当公路的坡度小于5%时，坡度越缓事故率越高.下坡坡度取值中等，即坡度取3%～6%时，坡度事故率较低，安全性提高.由于二级公路为双向车道，同一坡段存在上坡与下坡两种情况.综合数据可知:二级公路设计速度60 km/h，纵坡设计时取值3%具有较高安全性.由图1（c）至图1（h）可知，随着竖曲线半径、坡长、竖曲线切线长、圆曲线半径和缓和曲线长的增大，事故率逐渐增加.由图1（i）和图1（j）可知，平曲线长及转角角度变化对路段事故率的影响不明显，各指标取值下的事故率较为平稳.根据各指标下的路段事故率对线形指标进行风险评级:0～20%事故率为低风险，等级为1；20～40%事故率为中风险，等级为2；40%以上事故率为高风险，等级为3.各指标的评价等级见表1.

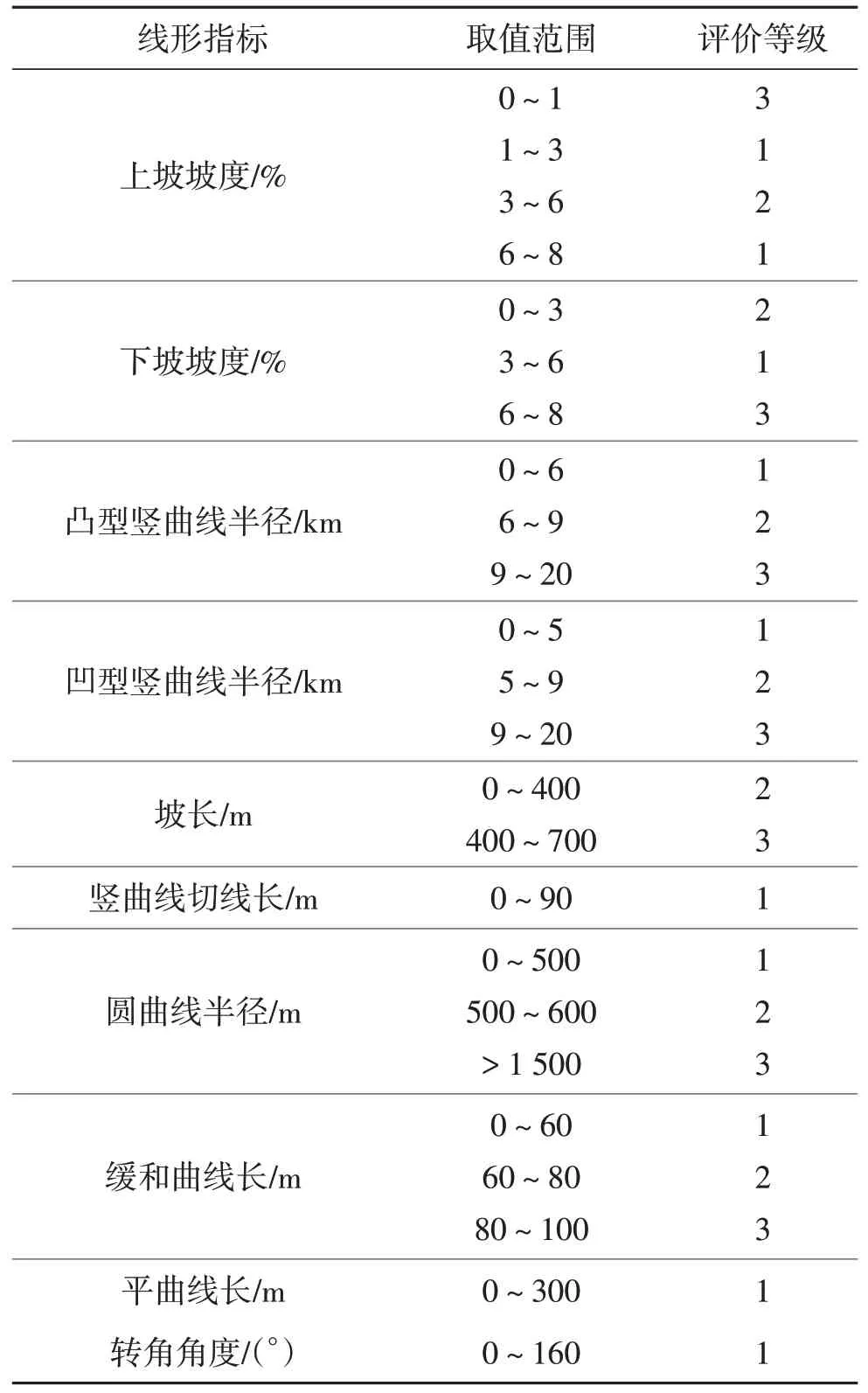
表1 线形指标风险评价等级Table 1 Risk evaluation grade of alignment indicators

2 基于事故数的风险指数权重

2.1 BP神经网络模型

BP 神经网络是一种多层前馈神经网络，常用于非线性函数中，是针对权值和阈值进行多次训练的一种网络模型.采用神经网络模型进行交通事故分析，具有强非线性逼近、自学习和检测率高的优点.研究表明，神经网路技术在处理分类问题上具有优势［15］.道路交通事故影响因素中线形指标类型较多，各线形指标对事故发现呈现非线性影响，因此采用神经网络模型进行权重分析具有安全机理上的可靠性.本研究采用3 层神经网，分别为输入层、隐含层和输出层.在前向传递中，输入信号从输入层经隐含层逐层处理，直至输出层.每层的神经元状态只影响至下一层，同层内神经元之间无连接.当实际输出与期望输出不符时，进入误差的反向传播阶段:根据输出值与期望值的误差，更新隐含层与输入层的权值，以及隐含层的阈值.算法程序将纵坡坡长、纵坡坡度、竖曲线半径（含凸型竖曲线半径和凹型竖曲线半径）、竖曲线切线长、圆曲线半径、缓和曲线长、转角和平曲线长共8个因子作为输入变量.为避免在事故分析时只考虑事故次数而不考虑其严重性，本研究通过综合考虑事故次数、受伤人数和死亡人数得出当量事故数，并以此作为输出层的因变量，可客观量化样本内各事故的严重程度.当量事故数为

其中，A为绝对事故次数；B为事故死亡人数；C为事故受伤人数；K1为事故死亡权重；K2为事故受伤权重.借鉴文献［25］，K1和K2分别取2.0和1.5.

BP 神经网络隐含层采用双曲正切激活函数，输出层激活函数采用恒等函数，错误函数采用平方和函数，以培训错误最小相对变化0.000 1 及预测误差未减少情况下的最大步骤数1作为迭代终止条件.训练并优化BP神经网络模型（图2）.其中，偏差用于将激活函数向左或向右移动，H（1∶1）～H（1∶12）表示第1～12个独立隐含层单元.

图2 基于BP神经网络的公路平纵线形指标风险指数模型Fig.2 Risk index model based on the BP neural network.

2.2 计算结果

将历史事故数据代入已训练的BP 神经网络模型，量化分析道路平纵各线形指标与道路交通当量事故数的关系.研究得出各线形指标对事故的影响权重，及百分化权重（即以影响权重最大的因子的权重度为100%，计算其余因子相对权重占比），见表2.

表2 各线形指标权重Table 2 Weights of each alignment indicator

3 线形风险指数计算及分析

通过历史事故数据，分析道路线形指标与道路交通事故之间的关系.以上述BP 神经网络模型求得基于当量事故数的各因子影响权重，综合线形指标权重系数及风险评级，建立风险指数模型为

其中，F为路段风险指数；Pi为第i个线形指标下的评价指数；ωi为第i个线形指标权重，本研究取表3中规范化的权重.

风险指数模型计算的依据是以事故率进行风险评级，采用事故数为输出变量的BP 神经网络模型求解各因子权重，综合事故率与事故数进行计算.采用固定步长累计频率曲线法求得事故多发段为K204+500～K206+500.事故多发段内发生事故的桩号分别为K204+500、K204+600、K204+700、K204+980、K205+200、K205+300、K205+500、K205+800、K205+900和K206+050、K206+500.对事故多发段处的风险指数进行分析见图3.

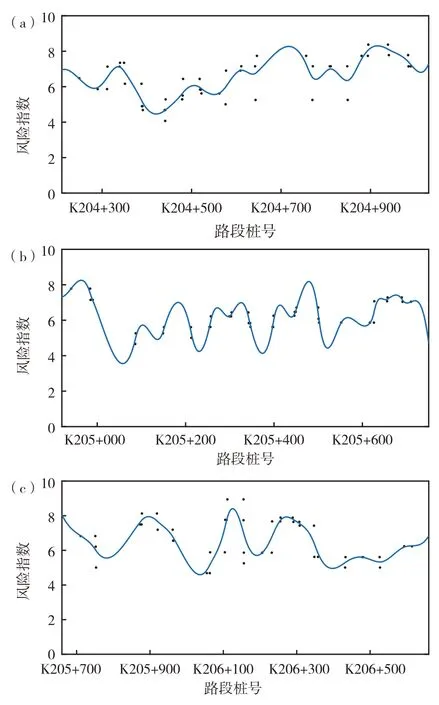
图3 事故点范围路段事故风险指数（a）桩号K204+500、K204+600、K204+700和K204+980；（b）桩号K205+200、K205+300和K205+500；（c）桩号K205+800、K205+900、K206+050和K206+500Fig.3 (Color online) Accident risk index diagram of accident point range road section for (a) piles K204+500、K204+600、K204+700、K204+980,(b) piles K205+200、K205+300、K205+500,and (c) piles K205+800、K205+900、K206+050、K206+500.

由图3 可见:①事故桩号K204+500、K204+600、K204+700 和K205+900 处于风险指数变化的峰值处，事故桩号点前100 m内风险指数逐渐升高至波峰，为导致事故致因段；②事故桩号K204+980、K205+200、K205+300、K205+500、K205+800、K206+050 和K206+500 处于高风险指数路段转向低风险路段范围，风险指数波峰在事故桩号点前100 m 内.事故桩号点前200 m 至前100 m 风险指数由低变高在桩号点前100 m处达到峰值，即前200 m内风险指数增高，存在导致事故的潜在原因.

为了验证本研究方法的可靠性及准确性，选取贵州省另一条二级公路进行验证，设计速度为60 km/h.采用累计频率曲线法求解事故多发段为K40+000～K41+000.事故桩号为K40+100、K40+200、K40+220、K40+300 和K40+500.通过实例进一步分析可得出事故致因段桩号为K40+000—K40+100、K40+100—K40+200、K40+120—K40+220、K40+200—K40+300和K40+400—K40+500，潜在风险路段桩号为K39+900—K40+100、K40+000—K40+200、K40+020—K40+220、K40+100—K40+300 和K40+300—K40+500.事故多发段内桩号处的风险指数见图4.

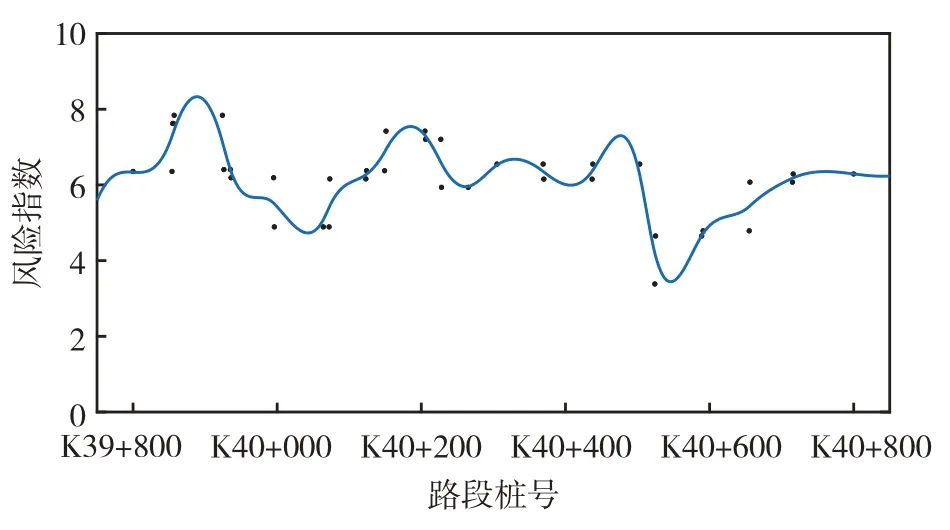
图4 验证路段事故风险指数Fig.4 (Color online) Validation of the road accident risk index diagram.

事故多发段处的事故桩号存在两种情况，处于风险指数波峰及高风险指数转向低风险的变化路段.综合两种情况，事故桩号点前100 m内风险指数存在波峰，为事故致因段.事故桩号点前200 m内风险指数增高，为事故潜在风险路段.深入分析事故多发的危险区间，可用以精细化分析事故危险区间内的人、车、路和环境等其他因素的影响.

4 结论

1）通过分析各线形指标下的事故率变化及分布情况，可知随着竖曲线半径、坡长、竖曲线切线长、圆曲线半径和缓和曲线长的增大，事故率逐渐增加.二级公路设计速度为60 km/h，上坡坡度为3%时具有较高安全性.

2）建立以道路平纵面8 个线形指标（纵坡坡长、纵坡坡度、竖曲线半径、竖曲线切线长、圆曲线半径、缓和曲线长、转角和平曲线长）作为输入变量，以当量事故数作为输出变量的多层感知器BP 神经网络模型，量化分析道路平纵面各线形指标与道路交通事故之间的关系，得到各因子综合影响下的道路线形指标对交通事故的影响权值.

3）根据事故率确定评价等级，采用基于当量事故数的神经网络模型确定因子权重.综合考虑评价等级与因子权重建立风险指数模型，可以兼顾路段事故率及路段当量事故数的影响情况.

4）研究发现事故桩号并不能准确反映事故致因路段，事故制动路段前的道路线形存在导致事故的风险.二级公路事故桩号点前100 m内为导致事故的风险路段，事故桩号点前200 m内为事故潜在风险路段.

本研究成果适用于交通量较低的山区二级公路，对其他设计速度的道路风险指数及事故区间范围需进一步深入研究.