考虑通信延时-丢包的配电网分布式电压控制
励刚,徐斌,王小明,,赵文广,方朝,吴红斌
(1.国网安徽省电力有限公司,安徽 合肥 230022;2.国网安徽省电力有限公司电力科学研究院,安徽 合肥 230601;3.合肥工业大学电气与自动化工程学院,安徽 合肥 230009)
随着“双碳”政策的实施,我国中低压配电网分布式电源并网数量迅速增加,截至2021年底,全国可再生能源发电装机容量达1 000 GW[1],有利于环境保护及社会经济发展。然而,高比例新能源发电并网对通信系统运行可靠性的要求不断提升[2]。考虑到分布式电源出力具有波动性、间歇性、不确定性问题及分布式电源装机容量较小、装机位置分散等问题,保证高分布式电源渗透下的配电网的电压安全稳定和经济运行具有重要意义。
目前针对含分布式电源的配电网控制策略主要分为就地分散控制、集中式控制和分布式控制三类。其中就地分散控制仅利用本地信息,但该控制方式无法实现协调控制,控制效果较差[3]。集中式控制需要采集和下发全局信息,对通信系统的实时性和信道的容量要求较高[4]。对于含高比例分布式发电的配电网系统,分布式控制方法可避免集中模型维护和优化求解,且采用反馈优化控制模式,分布式控制对状态波动具有更快的响应速度,具有更好的电压控制效果。文献[5]提出了一种基于分布式优化方法的配电网电压控制方法,通过构建面向大规模储能设备的协同控制框架以实现储能资源的规模化利用。文献[6]考虑通信设备故障对分布式控制系统运行的影响,提出了一种考虑多重通信故障的配电网失联分布式电源群优化控制方法。文献[7]针对传统电压控制方法受限于配电网模型参数精度的问题,提出了一种基于状态空间线性升维变换的主动配电网分布式电压控制方法,该方法不受参数不精确问题影响,具有较好应用前景。此外,分布式控制所需通信信道少,同时可实现分布式电源间协调控制,得到越来越广泛的应用[8]。
然而,配电网的通信网络建设在设备质量和数量上均远差于输电网络,实际运行中,分布式电源在空间上分布松散,节点间会不可避免地出现通信时延、丢包等通信问题[9]。传统的分布式控制算法设计基于理想的通信环境,对非理想通信环境下算法的收敛性、迭代速度等考虑较少,不利于实际的控制系统[10]。文献[11]分析了通信时延中的固定时延和时变时延对逆变器控制系统的影响,但并未考虑时延下系统的稳定性问题;文献[12-13]从系统通信网络方面进行改进,分别采用了能将传输延迟转化为固定传输延迟的时延控制器以及增加网络延迟补偿器补偿随机时延的方式应对非理想通信环境;文献[14]通过两步电压预测模型提出了一种不确定时延补偿策略,解决通信时延带来的控制系统不确定时滞问题;文献[15]分别采用预测控制方法、增益调度方法以及内环H∞跟踪控制方法,以确保在非理想通信影响下的电压控制稳定性,但是针对非理想通信环境下的控制方法有效性只在单个分布式电源条件下得到验证,在多分布式电源协调控制下的效果有待考证。
研究人员针对非理想通信条件下的多分布式电源的协调控制开展了卓有成效的研究,文献[16]针对网络攻击通信状态下的分布式协调控制策略进行研究,基于动态攻防博弈,建立了含分布式协同控制下的配电网风险评估指标。文献[17]通过构造时变一致性增益函数,利用含一致性增益函数的鲁棒协同一致性算法有效抑制了通信噪声和通信时延的影响,但算法的收敛速度和精度不理想。文献[18]对传统的分布式协调控制算法进行改造,设计了异步迭代架构和信息校验补偿机制,提高了非理想通信环境下算法的响应能力。但完全的异步迭代架构需要各分布式电源维护自己的时钟且迭代过程较为复杂。
为此,文章研究了在通信延时、通信丢包环境下的分布式控制方法,通过设计部分同步的迭代架构与引入一致性增益系统的方式加强了一致性算法在丢包、通信延时环境下的收敛速度;其次,以算法的收敛速度最小为目标,建立了分布式电源采样时间优化模型,提高了算法对该通信环境的适应性,最后通过仿真验证了所提策略的有效性。
1 部分同步迭代一致性算法
在配电网实际的运行过程中,通信延时、丢包等不可避免,例如信号的转换和传输可能产生延时、而延时过长则产生丢包等。配电网分布式电源间的通信网络系统如图1所示,假设分布式电源i与j存在通信线路,分布式电源i需要由智能电子设备接收并分析从系统状态测量单元测量的系统状态,然后通过通信系统进行数据转换,最后通过光纤网络进行传输,分布式电源j接收到通信信号后,同样需要经过通信系统的转换和基于智能电子设备的处理,将这个过程所经历的时间称为分布式电源i与j之间的通信延时,主要由两个部分组成:通信线路传输延时和通信系统转发和计算引起的随机延时。若分布式电源j在迭代周期内未收到分布式电源i的信号,则称为丢包。智能电子设备接收到由光纤网络传输的通信信息后,对信息进行处理、计算并进行分布式控制,以支持分布式应用。由于智能电子设备进行决策依赖于通信信息,在配电网分布式电压控制过程中,对通信质量有较高要求。若智能电子设备无法及时接收到其他智能电子设备的通信信息,这种情况下智能电子设备可能会因为信息不充足而做出错误决策,进一步影响分布式电压控制效果。
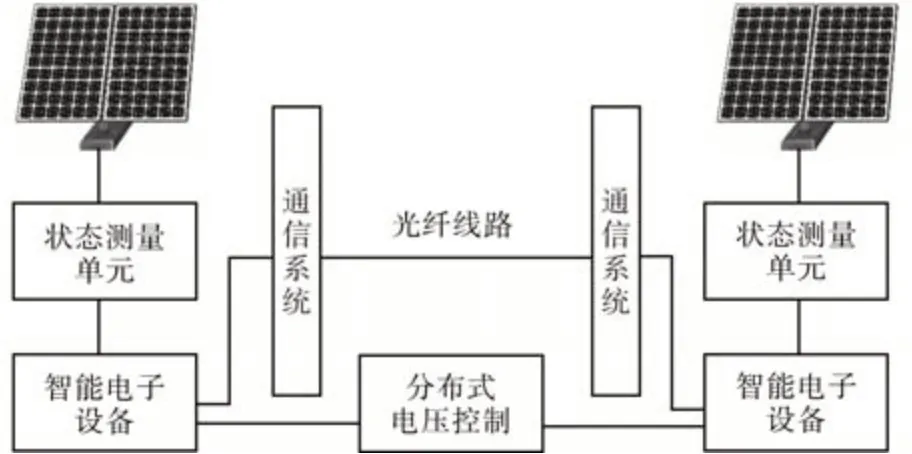
图1 分布式电源间通信过程示意图Fig.1 The communication process between distributed generations
上述通信过程的非理想通信因素会导致分布式电源间的信息传输出现偏差,从而影响分布式一致性算法的收敛速度以及收敛精度。假设节点i只与节点j通信,则令xij(t)为在通信延时、丢包环境下的智能体i所接收到的智能体j的信息,可以表示为
式中:γij(t)为丢包场景对系统的影响,γij(t)∈[0,1],当值为0 时,表示分布式电源i在t时刻无法接收到分布式电源j的传输信号,当值为1 时,表示分布式电源i在t时刻成功接收到分布式电源j的状态信息;τij为节点i与节点j之间的通信时延。
在离散时间一致性算法中,时延是指系统发送端到接收端的通信延时Tτ与固定采样时间T之间的差值,如下式所示:
在当前一致性算法迭代计算过程中,算法的迭代架构为同步迭代,即在每一次迭代过程中,每一个分布式电源都需要等待所有相连分布式电源的传输信号。若分布式电源运行和处理数据的速度较慢,或分布式电源间的通信条件较为恶劣,将使分布式电源的逆变器调节滞后于系统功率变化,在通信环境较为恶劣的情况下采用同步迭代方法,无法保证系统运行状态稳定,甚至会对系统的稳定运行产生不良影响。因此,提出了“部分同步”的一致性算法迭代架构。
实际分布式系统中,一致性算法的迭代过程为离散的,分布式电源每隔固定的采样时间进行数据更新迭代。对于一个分布式系统,假设这个固定采样时间为T,系统迭代次数为k,则每隔时间长度T进行一次迭代计算,考虑延时的一致性算法可以表示为
对于同步迭代一致性算法,若达到分布式电源的采样时刻时,因为延时导致通信信号并未完全传递,此时系统需等待信号接收,其控制时间轴如图2所示。在没有通信时延情况下,一致性算法的迭代计算时刻将分别位于k,k+1 时刻,如果时刻k时系统经时延τ后才接收到信息,然后进行迭代计算,此时原k+1 时刻的迭代计算将推移至k+1+τ时刻进行迭代计算,系统的迭代完成时间相应往后推移τ。
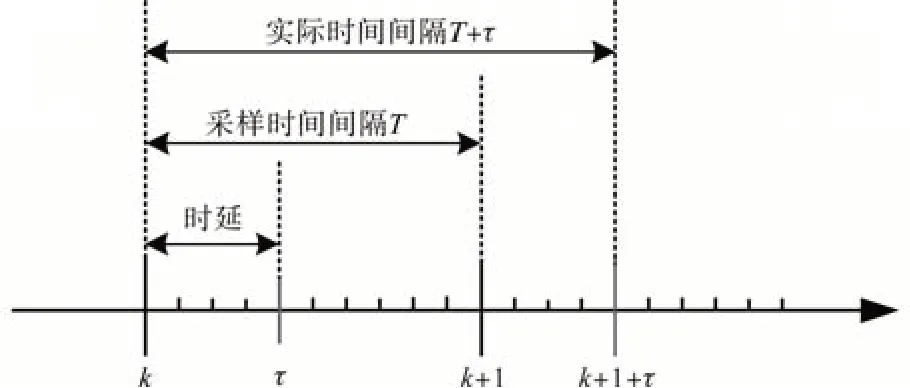
图2 同步迭代一致性算法控制时间轴Fig.2 Timeline of synchronized iterative consistency algorithms control
相邻节点的不同通信信道之间的通信延时通常不一致,计算得到的时延也不一致。因此,通过改变系统的采样间隔,可以在一定程度上改变系统的时延,甚至可以完全消除时延,但存在因采样间隔增大导致系统的收敛时间增加的问题,如图3所示。针对此问题,引入“部分同步”的一致性算法迭代架构来代替“完全同步”。在分布式系统的迭代计算过程中,根据分布式系统中的通信延时分布情况,设置适当的采样时间T。对于通信延时小于采样时间T的通信信号,在采样计算时刻利用目前节点所接受到的信息进行迭代计算;对于通信延时大于采样时间T的通信信号,则认为节点之间的通信信息发生丢包事件。此时,一致性算法更新为

图3 通信延迟与采样时间的时间轴Fig.3 Timeline of communication delay and sampling time
式中:μ'为电压调节系数;H(k)为k时刻主导节点的控制输入;σ'为旗帜变量,在节点为主导节点时为1,否则为0。
此外,为了保证在通信延时、丢包的影响下一致性算法的收敛精度和收敛速度,在一致性算法中引入一致性增益系数[21],此时,一致性算法可以更新为
其中
式中:c(k)为一致性增益系数。
在该算法的迭代结构下,计算缓慢、通信条件恶劣的节点与相邻的节点的信息交换、更新频率将远小于计算快、通信条件好的节点。该算法提高了一致性算法的收敛速度,但会导致丢包情况的增加,因此,针对算法运行中的丢包情况,重复利用上一时刻的控制信息,提升算法对丢包情况的适应性,加快算法的收敛速度。
2 考虑随机通信延时的采样步长优化模型
上文设计了一致性的算法的部分同步迭代架构,下一步需设置适当的采样步长,加快算法收敛速度。为此,在考虑通信系统随机延时的基础上,建立了考虑随机通信延时的采样步长优化模型。
2.1 随机通信延迟模型
固定路径上的分布式电源i与j之间的通信延时,主要由通信线路传输延时和通信系统转发和计算引起的随机延时两个部分组成,故需要对这两个部分的不确定性进行分别建模。
用φ1表示固定路径上的通信线路传输延时的概率密度函数(probability density function,PDF),用φ2表示固定路径上的通信系统转发和计算引起的随机延时的概率密度函数,则任意时间固定路径上的总延时的概率密度函数为
式中:p为通信线路上没有信号传输的概率。
通信线路传输延时和信系统转发和计算引起的随机延时的PDF关系为
其中,通信系统转发和计算引起的随机延时的概率密度函数φ2可以用一个正态分布函数来表示,如下式:
式中:μ,σ为形状参数,μ大于系统最短延迟时间。
当通信线路传输信号时,线路传输延时的概率密度函数φ2可以用幂指函数表示:
式中:λ为通信线路上信号传输周期的平均长度。根据式(9)~式(12),推导可得固定线路上的总延时概率密度函数为
对固定线路上的总延时概率密度函数φ(t)积分,得到累积分布函数F(t)如下:
2.2 考虑随机通信延迟的采样步长优化模型
为得到分布式系统的部分同步迭代一致性算法下的最优采样时间间隔,在考虑上述通信延迟随机性的基础上,以系统一致性算法的收敛速度最小为目标,以系统采样时间为优化变量,建立了考虑随机通信延时的采样步长优化模型。
2.2.1 目标函数
上文已经表明采用部分同步迭代架构时,系统采样时间的选取将直接影响到算法的收敛速度。因此,为获得合适的采样时间,模型从一致性算法的收敛时间的角度设立了目标函数,可以表示为
式中:K为系统收敛时的一致性算法的迭代次数。
2.2.2 约束条件
在进行求解的过程中,需要对相关变量的边界范围进行一定约束,考虑到分布式系统的物理特征以及所连接的DG 和通信系统的特性,相应的约束条件可以表示如下:
1)潮流约束:
式中:Pi,Qi分别为节点i的有功功率和无功功率;Ui,Uj分别为节点i和节点j的电压;Gij,Bij分别为节点i和节点j之间的电导和电纳;δij为节点i和节点j之间的相角差;PDG,i,QDG,i分别为节点i上DG 注入的有功功率和无功功率;Rij,Xij分别为支路ij的电阻和电抗;Pij,Qij分别为支路ij上末端的有功功率和无功功率;Iij为支路ij的电流。
2)各分布式电源有功出力约束:
3)各分布式电源无功出力约束:
4)采样时间间隔约束:
式中:m为通信系统的最短通信延迟。
5)节点间分布式电压约束。由于所提方法具有进行节点间电压控制的能力,对各节点的电压受控过程进行建模,在满足式(16)~式(21)约束条件的基础上,对部分同步一致性算法下的电压控制进行建模,利用k对电压进行时间标度,如下式所示:
式中:ui,k为k时刻节点i的电压标幺值;Vmax,Vmin分别为系统节点的电压上限1.05(标幺值)和下限0.95(标幺值)。
由于部分同步一致性算法在发生通信丢包时可以利用先前的通信信息对节点电压进行约束,因此将节点电压约束上、下界设定为当前时刻k和前一时刻k-1 的逻辑或值,并规定在通信正常情况下选择当前时刻k的约束值,在丢包情况下选择k-1 时刻的约束值。在这种情况下,由于通信丢包的影响,各节点间的电压约束随时间更新不完全同步,节点之间会出现频繁的潮流变化。因此,通过该约束可实现各个节点电压的之间的功率潮流。
通过以上5个约束条件可以实现在部分同步一致性算法下,节点之间按照通信信息进行分布式电压控制,确保分布式电源接入情况下的电压稳定。
3 模型求解
考虑到优化模型为同时包含等式约束和不等式约束多变量非线性优化模型,且模型中包含着一致性算法的迭代过程,求解较为复杂,常规的线性规划难以解决。粒子群算法(particle swarm optimization,PSO)可用于解决线性规划问题,然而粒子群迭代更新针对非凸非线性等问题常常陷入局部最优。因此,采用改进粒子群算法(improved particle swarm optimization,IPSO)对模型进行求解,由于部分同步一致性算法的约束参数具有时变特性,动态调整粒子群算法中的惯性权重w,以确保在求解非线性规划问题时算法也具有较高的精度。算法迭代过程中,每个粒子的位置和速度的更新方式可以表示为
式中:w为惯性权重;c1,c2为加速系数;r1,r2为0 ~1的随机数;k为粒子群算法的迭代次数。
基于粒子群算法的模型求解的主要步骤如下:
步骤1:数据初始化,输入配电网的拓扑数据和分布式电源容量数据;
步骤2:设置粒子群迭代参数w,c1,c2,通信延时模型参数p,μ,σ,λ;
步骤3:设置N个粒子的初始速度和初始位置,动态调整算法中的惯性权重w,引入变异的思想,在特定情况下对粒子进行初始化,多样性公式表示如下:

若dt≥dhigh,则w=wmax;若dlow<dt<dhigh,则w=wmax-(dhigh-dt)(wmax-wmin)/(dhigh-dlow);若dt≤dlow,保留全局最优值和个体最优值,并重新执行该步骤;
步骤4:将每个粒子放入场景中,进行一致性算法迭代计算,期间若通信信道的通信延时大于粒子所代表的采样时间,则视为丢包;
步骤5:计算每个采样时间下的目标函数值;
步骤6:将粒子的适应度值分别与个体最优值和群体最优值比较,并更新这两个最优值;
步骤7:判断是否满足迭代收敛条件,如果不满足,进入步骤8,否则跳转步骤9;
步骤8:根据式(23)的粒子群更新迭代规则,更新速度和位置向量,跳转步骤3;
步骤9:计算结束,获得系统的最优采样时间,输出优化结果。
4 算例分析
4.1 算例参数
为验证所提模型的有效性,仿真基于Matlab 2018b 平台,采用标准IEEE-33 节点系统进行仿真验证。在网络架构方面,算例分别在标准节点算例系统中的节点7,10,13,17,18,21,25,26,28,33 接入额定有功功率分别为200 kW,500 kW,600 kW,800 kW,600 kW,400 kW,400 kW,800 kW,800 kW 和600 kW 的分布式电源,设置节点的电压上下限分别为1.05(标幺值)和0.95(标幺值)。正常运行时,一致性算法主导节点设置为节点17处的分布式电源。综上,算例系统基本结构如图4所示,图中分布式电源之间的虚线连接为额外的通信线路。
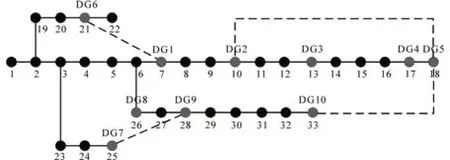
图4 IEEE-33节点算例系统图Fig.4 The IEEE-33 node example system
4.2 通信延时概率分布模型
根据文中所提出的分布式通信路径上延时的概率密度函数和累积分布函数,函数中相关参数p,μ,σ,λ分别设置为0.58,22,150,1.39,通信系统的延时累积分布函数如图5所示。

图5 通信延时累积分布函数Fig.5 Distribution function for communication delay accumulation
4.3 部分同步架构控制结果分析
设置改进IPSO 算法粒子个数为100,迭代次数为200,惯性权重为0.9,最小惯性权重为0.2,加速系数c1和c2均为2,经模型优化后得到算例系统的最优采样时间为30 ms。部分同步算法迭代计算后,得到系统到达稳定状态的节点电压如图6所示,系统的分布式电源无功功率利用率的一致性算法迭代曲线如图7所示。
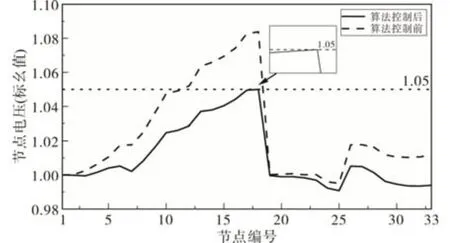
图6 节点电压曲线对比图Fig.6 Comparison results of node voltage curves
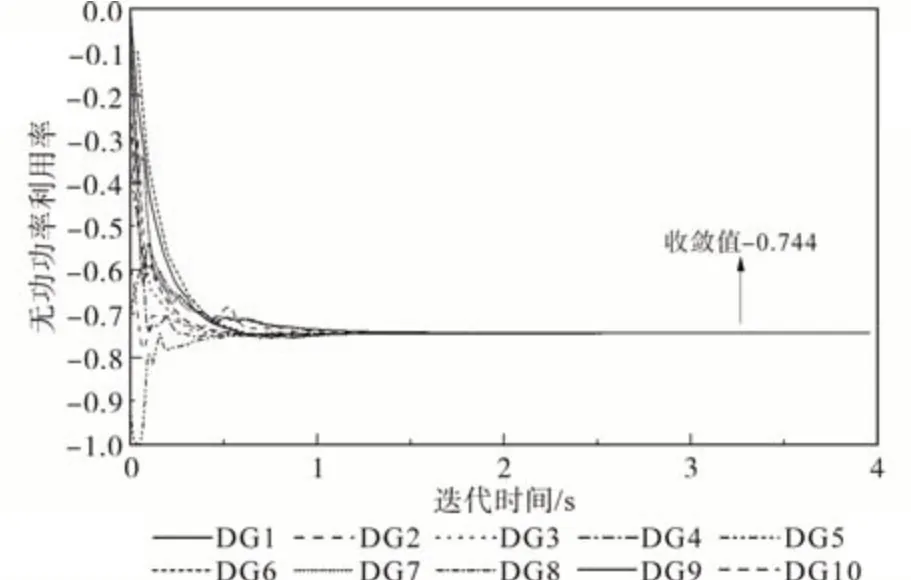
图7 部分同步迭代一致性算法的无功功率利用率收敛曲线Fig.7 Convergence curves of reactive power utilization using partially synchronous iterative consistency
由图6、图7 可见,分布式电源初始无功功率利用率分别为0,-0.2,-0.4,-0.7,-0.9,-0.1,-0.1,-0.4,-0.6,初始时各分布式电源的无功功率利用率差距较大,拓扑末端分布式电源无功功率利用率达-0.9,而拓扑首端的节点的分布式电源的无功功率利用率仅为0,-0.1 等,此时部分分布式电源基本没有参与系统的电压控制,经一致性算法的迭代计算后,系统各分布式电源无功利用率均稳定收敛于一致值(-0.744),系统各节点电压收敛值在规定范围内。
当算例系统的采样时间设置为30 ms 时,经部分同步迭代的一致性算法计算后,33个节点的电压均能维持在正常范围,其中节点18的电压降至1.05(标幺值)以下,相对初始状态的节点电压分布情况,系统电压越限情况明显改善,此时,一致性算法收敛大约需要118 次迭代,共需迭代时间2.74 s,收敛时间较短,通过迭代能稳定收敛至-0.744。在算法迭代过程中的前1 s,系统各分布式电源无功利用率的变化较大,且具有波动趋势,这是因为部分同步迭代的过程中对丢包情况的复用信息的影响,但随着系统趋于稳定,该影响逐渐减低,系统波动性减小,如图7 中1 s后的迭代曲线,系统各分布式电源无功利用率逐渐稳定。
通过计算各个节点的电压变化来表征分布式电压控制对全网潮流产生的影响,结果如图8所示。算例将一致性算法主导节点设置为节点17 处的分布式电源,由图8 可见,节点17 及相邻节点18、节点19 的电压越限情况改善最为明显,表明节点17 与节点18、节点19 之间的分布式电压控制最为有效。由图4 可知,33 节点与节点18相接,结合图8可见,该算例中节点电压改善效果由一致性算法主导节点17 至其余相邻通信节点依次降低,可见所提分布式电压控制对全网潮流产生了较好的改善效果。

图8 节点电压潮流变化图Fig.8 The node voltage flow variation
4.4 同步迭代与部分同步迭代性能分析
为验证文章所提出的部分同步迭代架构的有效性,采用同步迭代架构一致性算法进行对比。在相同的仿真条件下,以分布式电源无功利用率为一致性变量对算例系统的电压进行协同控制。为提高算法的收敛速度,引入一致性增益系数来提高收敛效果,仿真分析了通信系统的随机延时和丢包对不同迭代策略的收敛时间的影响,仿真结果如图9所示。

图9 同步迭代一致性算法的无功功率利用率收敛曲线Fig.9 Convergence curve of reactive power utilization using synchronous iterative consistency
以节点18处的DG5为例,比较软中断通信环境下同步迭代与所提出的部分同步迭代中DG5的无功功率利用率迭代曲线,如图10所示。

图10 两种策略下DG5无功功率利用率迭代曲线图Fig.10 Iterative curves of reactive power utilization of DG5 under two strategies
对比两种策略下的无功功率利用率曲线、迭代次数和迭代时间结果如表1所示。其中同步迭代一致性算法大约迭代103次后一致性变量趋于收敛,并收敛于-0.744,迭代共需时间3.42 s。而部分同步迭代一致性算法大约迭代118次后一致性变量趋于收敛,并收敛于-0.744,迭代共需时间2.74 s。迭代过程中,同步迭代策略曲线较为平滑,但迭代速度较慢,算法易受部分恶劣通信环境的信道影响。由于部分同步迭代架构会将通信延时大于采样时间的信道信息认定为丢包,使丢包情况增加,导致部分同步迭代架构在算法迭代初期波动较大,影响了算法的收敛速度。复用控制信息的方式降低了丢包对算法的影响,但也增加了算法迭代过程中的波动,随着迭代次数的增加,这种不利影响逐渐减小。此种情况下,由于部分同步迭代每次迭代所需时间更短,使得算法能以较短的时间收敛。因此,所提出的部分同步迭代架构在软中断通信场景下较同步迭代相比有明显优势,对高渗透率配电网的分布式电源无功功率的协同控制具有重要意义。

表1 同步迭代与部分同步迭代的性能比较Tab.1 Performance comparison between synchronous iteration and partial synchronous iteration
4.5 采样步长优化模型有效性分析
为分析所提出的考虑随机通信延时的采样步长优化模型的优化效果,基于图4 的算例系统,在相同的仿真条件下,以分布式电源无功利用率为一致性变量对算例系统的电压进行协同控制,且算法架构均采用所提部分同步迭代。将三组对比算例的系统采样时间间隔分别设定为25 ms,32 ms,40 ms,仿真获得不同策略下的一致性算法的收敛过程曲线。以算例系统的DG3 为例,不同采样时间间隔的收敛过程如图11、图12所示。
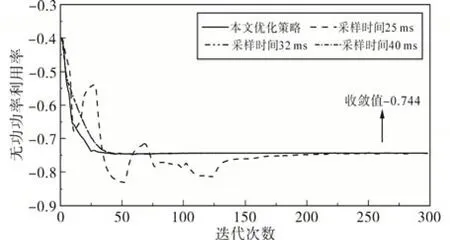
图11 不同采样时间间隔下的一致性算法收敛曲线Fig.11 Convergence curves of consistency algorithm under different sampling time intervals

图12 四种采样时间下DG3节点电压迭代曲线Fig.12 Iterative curves of node voltage at DG3 under four sampling times
如图11 和图12所示,四种采样时间间隔策略下,经一定次数的迭代,部分同步迭代一致性算法均能稳定地收敛至稳定值-0.744,DG3 接入节点的电压标幺值均能从初始值1.063(标幺值)降低至1.037(标幺值)。对比四种策略下的分布电源无功功率利用率收敛曲线和节点电压迭代曲线可见,当采样时间小于优化策略所得的结果时,一致性算法迭代过程出现较为明显的波动,波动范围随着迭代次数的增加逐渐减小至收敛。这种现象的原因是此时采样时间较短,有大量通信信息因通信延时较大被判定为丢包,丢包的大量存在使得系统的收敛速度大大降低。当采样时间大于优化策略所得的结果时,系统一致性算法的迭代过程更加平稳,但迭代时间明显增加。
各策略下具体迭代次数和迭代时间如表2所示,当采样时间为25 ms 时,一致性算法迭代286次后一致性变量趋于收敛,共需迭代时间5.77 s。而采样时间为32 ms和40 ms时,一致性算法迭代109 次和106 次后一致性变量趋于收敛,共需迭代时间分别为4.15 s和4.64 s。由此可见,提出的优化策略在收敛速度和收敛稳定性上有较为明显的优势,可显著降低一致性算法的收敛时间。
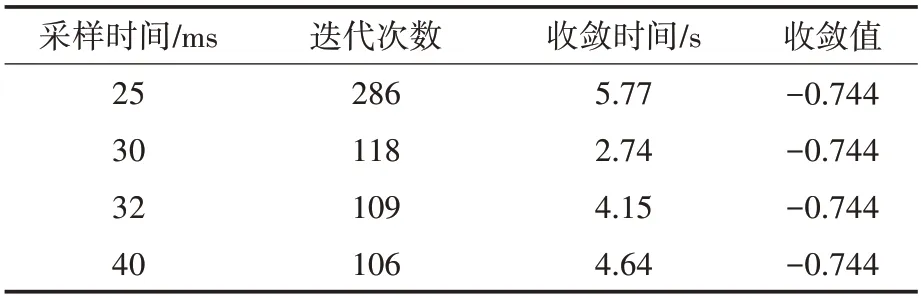
表2 部分同步迭代下不同采样时间步长的性能比较Tab.2 Performance comparison of different sampling time steps using partial synchronous iteration
5 结论
以当前软中断通信环境下的同步迭代一致性算法为切入点,针对同步迭代架构易受到个别通信条件恶劣的分布式电源的影响导致收敛速度降低的问题,研究了算法在通信延时、丢包环境下的改进措施,通过设计部分同步的迭代架构并引入一致性增益系统,提高了一致性算法在丢包、通信延时环境下的收敛速度。在此基础上,建立了考虑随机通信延时的采样步长优化模型,模型通过以算法的收敛时间最短为优化目标,经粒子群算法求解出一致性算法的最优迭代步长,最后在IEEE-33 节点标准算例系统中进行了仿真验证。结果表明,文章所提出的方法能够有效降低通信延时、通信丢包等非正常通信环境对系统安全稳定运行的影响,提升一致性算法的收敛速度。

