基于状态估计方法的相量测量单元电压稳定性研究

蒋文辉，林冬，于力，陈波，陈煜敏

（南方电网数字电网研究院有限公司，广东 广州 510000）

2021年，全社会用电量83 128 亿kW·h，同比增长10.3%，较2019年同期增长14.7%，两年平均增长7.1%。其中，第一产业用电量1 023亿kW·h，同比增长16.4%；第二产业用电量56 131亿kW·h，同比增长9.1%；第三产业用电量14 231亿kW·h，同比增长17.8%；城乡居民的生活用电量11 743亿kW·h，同比增长7.3%。与此同时，可再生能源发电装机比重超过1/3。但电力工业在取得巨大成绩的同时也面临着严峻挑战。

一般的电力系统由发电机、变压器、母线、输配电线路及各种用电设备组成。各电气元件及系统通常处于正常运行状态，但也可能出现故障或异常运行状态。随着电力系统的规模越来越大，结构越来越复杂，故障产生不可避免。因此需要寻找静态电压稳定性的校正措施或控制方法和最优解，以敏锐地观察电力系统的动态，从而有助于理清问题。同时也有助于对系统进行有效规划，使相互依赖的关键基础设施更加可靠地运行。

针对上述存在的问题，现阶段已经进行了多项研究并且找到可以实现静态电压稳定性的校正控制。快速控制和在线解决方案以及对系统进行实时监控，都可以对静态电压稳定性问题进行有效缓解。文献[1]分析了电网工程的发展现状和满足大电网综合防御体系的建设需求，提出了系统架构设计方案，该系统能够准确识别系统故障状态，实时判别策略逻辑，通过切机及功率转带等措施，实现电网的快速、稳定控制。文献[2]分析了连云港地区电网在线安全预警系统管理现状，提出了现阶段预警系统的不足之处，最后对连云港地区电网在线安全预警系统进行了设计，并给出了设计方案及实现的4种预警功能。文献[3]分析了孤岛微电网静态电压稳定性，并提出了相对应的分析算法。

同步相量测量技术已经在电力系统控制保护等方面得了广泛应用，甚至在算法和模拟方面也得到了充分的应用，现在已成为实时电力系统中不可分割的一部分。虽然国内对电力系统电压稳定性评估方面的研究并不少，但是基本没有将相量测量单元（phasor measurement unit，PMU）运用到电压状态估计方面的研究。本文从介绍电压稳定性以及它在扰动下将如何偏离其工作点入手，重点介绍了如何将PMU 与传统状态估计技术结合以使系统故障可观测，并且讨论了PMU的最优配置问题。本文中的研究在考虑了负载变化的情况下，使用已给出的各种电压稳定性技术来分析电压稳定性。文中最后在Matlab/R2015a 软件上使用IEEE14 测试总线对文中所得到的结果进行了仿真分析，验证了实验结果的准确性。

1 方法和程序

1.1 相量测量单元

相量测量单元是一种监测设备，其数据采用相量形式，用正弦波的复数表示，包括电信号中的幅度和相位角。对于绝对时间参考，同步相量使用协调世界时（universal time coordinated，UTC）。因此，PMU 测量的电压和电流数据带有时间信息。一旦它们同步，就可以进行实时比较。相量测量单元由同步单元、测量单元和数据传输单元组成。同步单元包括全球定位系统（global positioning system，GPS）接收器和锁相振荡器，为测量单元提供采样时钟，同步精度甚至优于1 μs。测量单元具有3 个组件，即抗混叠滤波器、A/D 转换器和微处理器。抗混叠滤波器用于验证所有模拟信号的相同相移和衰减，A/D 转换器将信号从滤波器转换为数字信号。数据传输单元进一步传输测量数据。图1 显示了基本的PMU 结构。由于在每条总线上配置PMU 来诊断/检测问题区域的经济代价是很高的[4]，因此需要一种配置技术在减少PMU 配置数量的同时提供系统的完整可观察性。

图1 基本PMU结构Fig.1 Basic PMU structure

在这项工作中，PMU 的最佳配置由贪心算法完成。使用贪心算法[5]选择具有最大连通性的PMU 配置位置，以确保系统的可观测性，进而在很大程度上减少所有总线上安装PMU 的数量。为了确保算法的执行，本文中选择将导纳矩阵的元素转换为二进制数形式，得到维数为Nbus×Nbus的连通矩阵CPMU。矩阵的元素被定义如下：

式中：i，j为连通矩阵CPMU中的第i行第j列。

可知式（1）中的关键在于求∑Xi的最小值，其中Xi为配置PMU的总线，则有如下表达式：

其中

如果满足上述条件，则称系统为可观察的，否则称系统不可观察。为了总线的最大连通性，对CPMU的每一列求和。求出最高和的列，即为配置PMU的总线位置，表达式如下所示：

式中：SUM为一个1×Nbus的矩阵。

将PMU 配置在任何总线上，基于总线可观测性，对可见性矩阵再次进行相同维数的更新，其元素属于[0，1]。因此，与PMU添加的总线对应的行和列将从连接矩阵中删除。如果可见性矩阵的元素为1，则系统被认为是可观察的。具体遵循如下的步骤：1）读取电网中的可用数据。2）使用总线导纳矩阵，建立连接矩阵。3）推导出优先度的总线，选择该总线作为PMU 的位置。4）如果两个或多个总线具有相同的连接性，随机选择一个总线并将PMU配置到该总线。5）更新可见性矩阵。检查总线的可观察性。如果不可观察，则重复步骤3），否则结果总线是该PMU的唯一位置。

1.2 PMU状态估计方法

由于一般的数据采集与监视控制系统的常规测量在实时捕获系统动态方面还不成熟，无法完成对连续变化系统的状态估计，因此，需要对状态估计算法方案进行修改，使其能够处理和监控这些变化。PMU 可以很好地解决上述问题，因为它与GPS 通用时钟同步，可以直接测量其所在母线的电压和电流。因此，将状态估计测量与PMU 测量结合比单独使用状态估计用于整个系统进行测量更有效率，同时也更加准确。在给定的传输线模型中，可以通过线电流的大小来计算另一侧的电压。测量线路电流的优点是它可以将电压测量扩展到那些没有安装PMU 的总线。由此可以通过选择PMU 的最佳配置位置[6-8]来减少所需的PMU 数量，间接测量总线电压。方程可以描述为如图2所示的π 线模型，该π 线模型的数学表达式如下式所示：

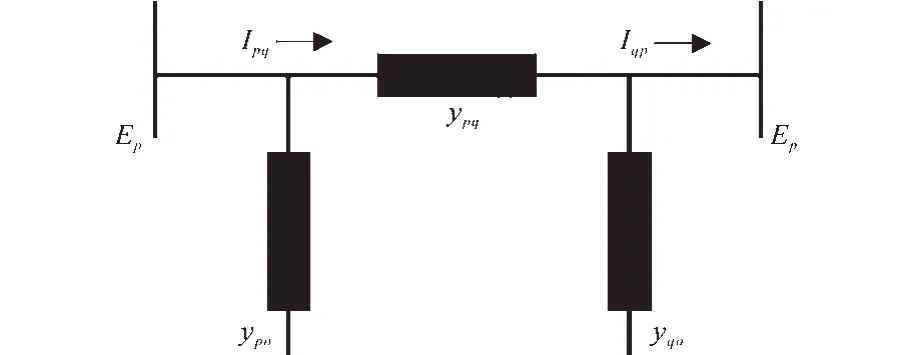
图2 π线模型Fig.2 π line model

计算步骤如下：

1）令m为未进行电流测量的总线编号，q为目前的总线的编号，p为未进行电压测量的总线编号。

2）计算m×q维的当前关联矩阵A。

3）计算m×m维导纳矩阵的对角线。

4）将每个pi部分的分流分支添加到对角矩阵。

5）得到由p和m组成的测量向量，表示为

式中：Z为测量向量；∏为删除缺失母线电压行的单位矩阵；y为当前线路的导纳向量；ys为已测量线路的导纳向量；Eb为线路端电压；B为线路状态矩阵。

6）计算估计值：

式中：X为配置PMU 的总线；M为状态估计矩阵；B，W，T为状态估计器的中间配置矩阵。

因为矩阵M可以将测量结果直接转换为状态估计器中的数据，所以上述等式可以使估计器成为线性的，它不像早期估计器那样会产生非线性估计，这也是本方案一个显著优点。

本文在传统的状态估计技术之上进行了最小二乘（weighted least squares，WLS）的处理。正如之前所知道的，状态估计是一个将值分配给基于该系统的测量而建立的未知状态变量的过程。这个过程可能涉及不精确的测量，但可以使用统计标准消除以获得真实值，然后使用这些值来最小化或最大化某些目标函数。WLS 涉及正规方程的迭代求解，对状态向量X0进行了初步猜测。对于对应的潮流解决方案，初始猜测被视为平坦的电压曲线，即所有母线电压都假设为每单位1.0。

1.3 电压稳定性

电压稳定性是指电力系统在受到干扰后保持所有母线电压恒定的能力。电压不稳定的一些原因是负载丢失、保护装置意外跳闸而导致级联中断，其中不稳定的主要原因是负载。级联中断是指由于电压不稳定，从而导致网络中持续较长时间的停电或异常低电压现象。这些过程通常被称为电压崩溃。可以根据干扰水平或持续时间进行分类，根据扰动水平，可分为大扰动和小扰动电压稳定性，而根据持续时间，可分为短期或长期持续时间[9]。

通过估计电压状态以及利用电压稳定性工具，可以正确估计电压不稳定性，并可以使用适当的校正措施将电压恢复到平衡点。利用牛顿-拉夫逊方法进行潮流分析，该方法为指定母线条件下的线路潮流和电压提供了解决方案。本文中使用的一些其他分析工具分析如下。

1.3.1 有功功率和无功功率的曲线

此分析将通过选择有功功率逐步增加的候选母线来完成，因此通过运行潮流程序计算相应的电压[10-12]，直到潮流不收敛。对于这些候选母线，绘制了P—V曲线，如图3所示。如果电压解为正，则P—V曲线的解给出稳定运行，否则不稳定，鼻尖描绘为最大负载的临界点。Q—V分析是通过改变无功功率来完成的，图4 显示了曲线底部的Q—V曲线，其中dQ/dV=0 为曲线底部，右侧描绘了Q和V都增加的稳定区域，而左侧描绘了Q减小V增加的不稳定区域。

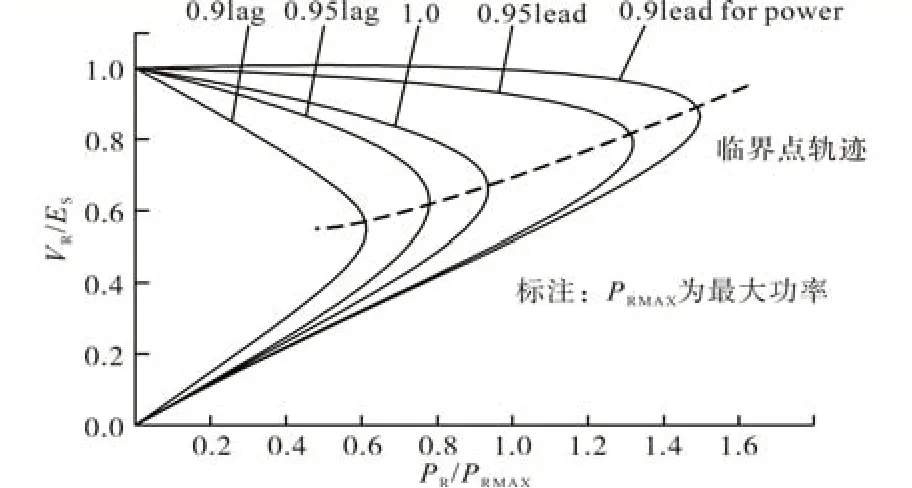
图3 P—V曲线Fig.3 P—V curves

图4 Q—V曲线Fig.4 Q—V curves

1.3.2 电压稳定指标

电压稳定指标（voltage stabilization indicator，VSI）表示电力系统不稳定接近度。故障从空载到电压崩溃，指数值的范围从0 到1。它们将揭示关键总线或总线之间连接线路的稳定性。如果发现母线处于临界状态，则必须采取某些纠正措施，例如使用串联、并联电容器和同步电容器。数学模型如图5所示。

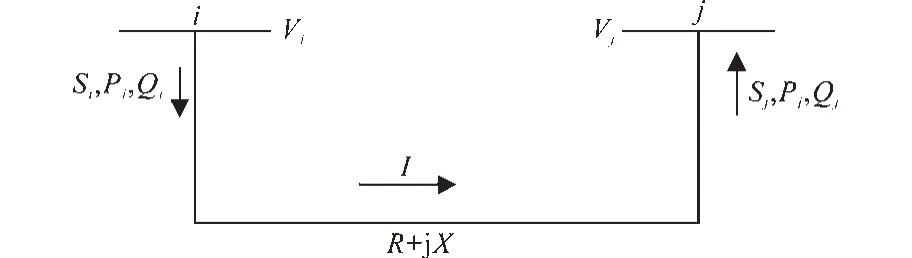
图5 电力线模型Fig.5 Power line model

图5 中，i表示发送总线s，j表示接收总线r。公式中使用的除此之外的一些符号描述如下：Z为线路阻抗；X为线路电抗；Qj为接收端的无功功率；Vi为发送端电压；θ为线路阻抗角；δ为电源之间的相角差；Pi为发送端的有功功率；Pr（max），Qr（max）为最大有功和无功功率；Ploss（max），Qloss（max）为最大有功和无功损耗；Vi，Vj为电压相量。

下面给出了一些使用指数的描述：

1）V/V0指数：这里V是从潮流获得的母线电压，V0是从潮流获得的新电压，同时保持所有负载为零。该比值将给出弱总线的有效检测。

2）线路稳定性指数Lmn：该指数可以从单条线路中使用的电力传输概念推导出来，其中电压二次方程的判别式大于零为实现稳定的运行条件，如果判别式的值小于零，则系统将不稳定。Lmn表达式如下式所示：

3）快速电压稳定性指数（fast voltage stabilization indicator，FVSI）和线路功率质量（line power quality，LQP）指标：这两个指数的概念与Lmn中使用的概念相同，但其公式有所不同，如下所示：

4）功率传输指数（power transmission indicator，PTI）：该指数表示通过线路传输的最大功率，如下所示：

2 实验结果

使用Matlab/R2015a 软件对如图6所示的标准IEEE14 测试总线系统进行仿真数据模拟。该系统有5 条发电机母线、20 条相互连接的支路和9条负载母线。

图6 IEEE14测试总线系统Fig.6 IEEE14 test bus system

使用牛顿-拉夫逊方法运行潮流程序，评估潮流的有功和无功功率以及电压及其角度，假设以下潮流的结果是准确的。

使用贪心算法[13-14]，过程不断重复，直到整个系统变得可观察为止。由实验结果可知，当PMU 被配置在4，6，2，9，7 总线上，可以实现IEEE14 总线系统的完全可观察性。这表明不需要将PMU配置在所有14条总线上，只配置在5条总线上即可。该方法的可靠性已经在IEEE5，30，57和118等不同的测试系统上进行了测试，证明它是一种有效的PMU布局方法，如表1所示。

表1 不同IEEE总线上PMUs的OPPTab.1 OPP of PMUs on different IEEE buses

在负载可变的情况下，绘制了有功功率和电压变化图，结果如图7所示。可以得出结论：随着负载在10 次实验中从70%增加到120%，在所有总线上，随着负载变化情况相对应的功率都会减小。实验结果出自于配置PMU的4号总线。

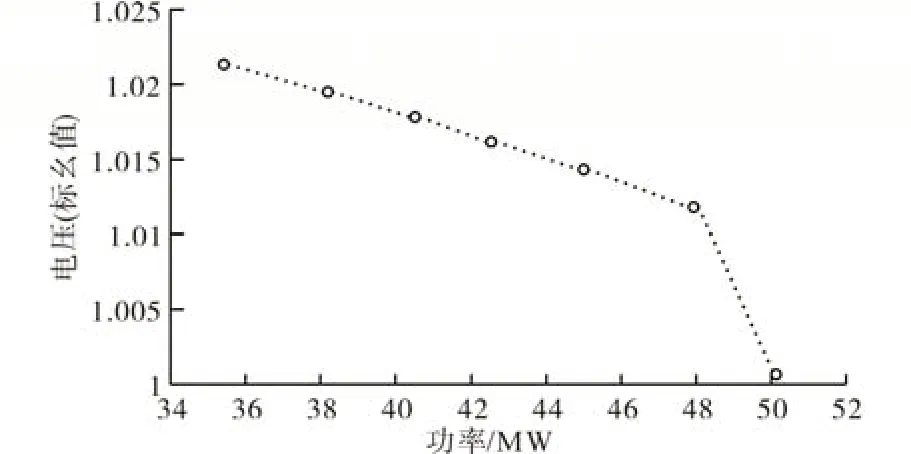
图7 P—V曲线Fig.7 P—V curve

图8所示为不同负载变化条件下所有母线的无功裕度变化图。从图8中可以推断出在系统经历电压崩溃之前母线的无功功率需求。通过观察配置PMU 的总线2，4，6，7和9分别接入负载率为0.750，0.900 和1.200 的不同负载条件下，可以发现，在所有这些可变负载中，母线7具有最低无功裕度，表明该母线是关键母线。在整个负载变化过程中，总线2 具有足够的无功裕量。除了7 号总线外，5 号、11 号和12 号总线也被认为是关键总线。

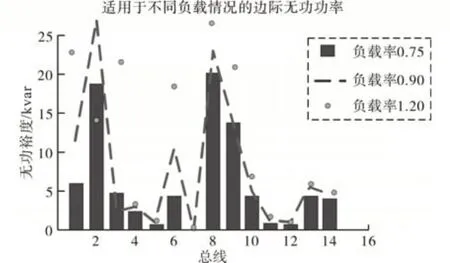
图8 无功功率裕度Fig.8 Reactive power margin

使用不同方法进行电压测量的比较结果显示在表2 中，其中电压测量结果均以标幺值的形式表示。根据电压V进行潮流计算的方法可降低不确定性水平，并具有良好的准确度水平和更少的计算时间。但是增加总线会导致迭代增加。迭代次数越多，需要的计算时间就越多。计算程序中没有考虑相位角偏差。

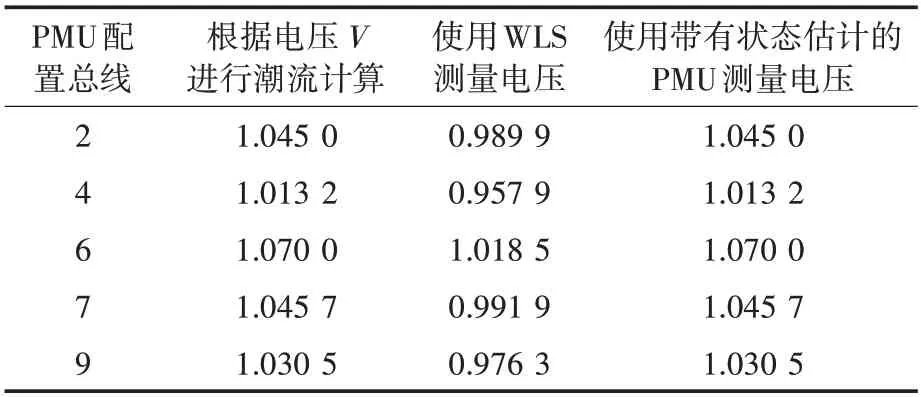
表2 使用不同方法进行电压比较Tab.2 Voltage comparison using different methods

通过对PMU 的直接测量，并利用线路电流的扩展来检测相邻母线电压具有显著的优点。矩阵M是一个转换矩阵，它测量电压和电流并提供线性估计。由于没有使用长迭代方法，所以它具有快速的计算速度。只要系统保持完好，条件就会得到满足。估计x具有与状态估计的传统方法相同的概念。

使用WLS 方法，可以看出从潮流中获得的基准电压值的差异。但是使用带有状态估计的PMU 直接测量提供了与潮流相同的结果，而无需任何迭代方法。由于潮流计算的电压值是精准的，这个估计提供的结果与潮流计算结果相同，表明它在IEEE14测试总线上的可行性。

下面对一些PMU 配置总线进行了各项指标的计算，并给出了指标结果，如图9、表3～表5所示。

表3 总线2上的指数比较Tab.3 Index comparison on bus 2

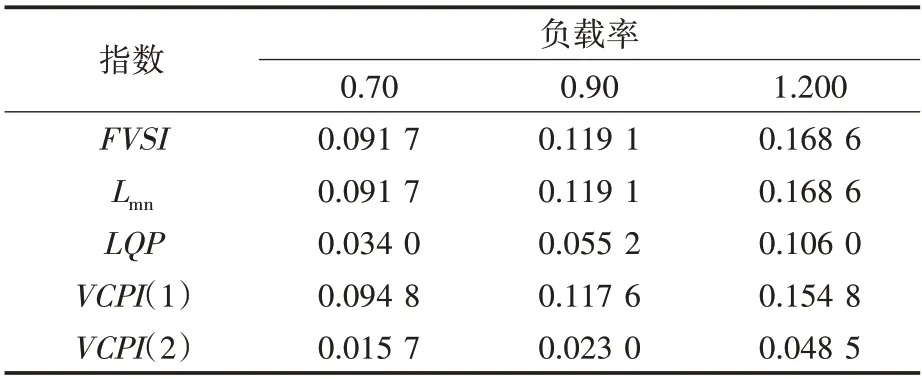
表4 总线4上的指数比较Tab.4 Index comparison on bus 4

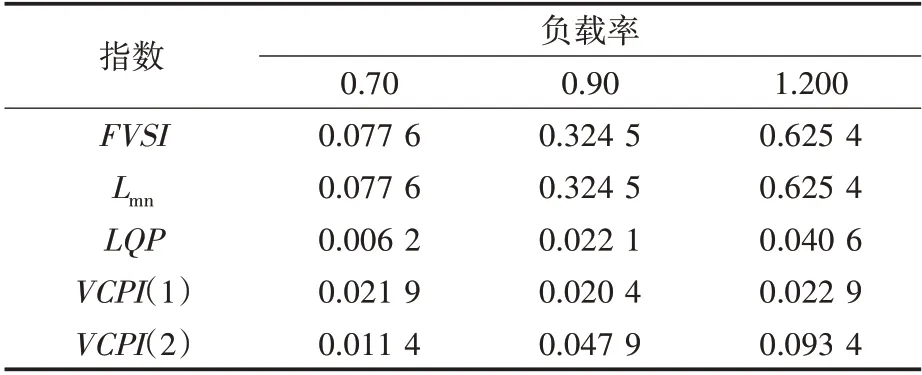
表5 总线6上的指数比较Tab.5 Index comparison on bus 6

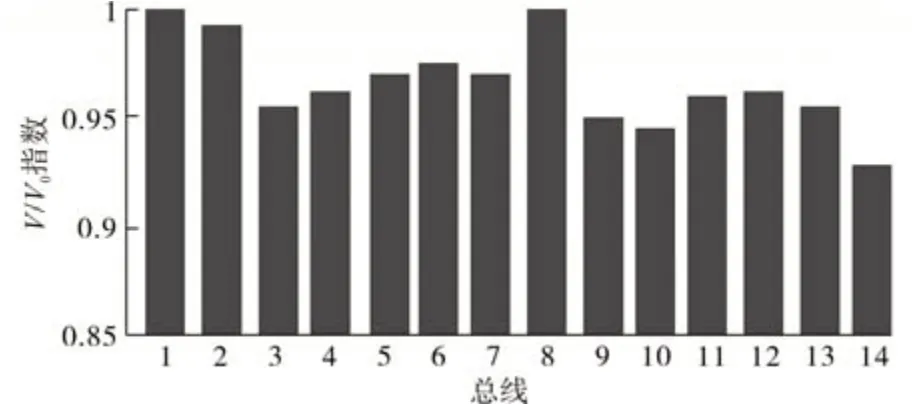
图9 V/V0指数Fig.9 V/V0 index

1）V/V0指数：从图9 中可以发现总线1，2 和8是关键总线，因为它们的指数在1以上。

2）FVSI和Lmn指数：从表3～表5分析，随着负载变化从0.70 增加到1.20，每条总线的指数值也增加，此外，这两个指数的值是相同的。这些变量的大小取决于无功功率。

3）LQP指数：同样的结论在这里也是有效的，负载增加时，每条总线的指数值也在增加。但是在极端负载条件下，母线2为关键母线。

4）VCPI指数：根据线路的最大功率传输能力来计算指数。分析表3～表5 的结果可知，随着负荷变化的增大，母线的变化使指数值增大。VCPI（Q）指数指的是最大无功功率，随着负载的增加，线路的临界值保持在0～1之间。

因此可以得出结论，在最大负载条件下，VSI各项指标值会更高，对应总线被称为临界线。

3 结论

本文提出了基于状态估计的相量测量单元测量电压稳定性的方法。通过利用Matlab/R2015a软件对IEEE14 测试总线进行仿真分析。在变化的负载条件下，绘制了P—V曲线和无功裕度与母线的曲线，表明随着负载的增加，功率减小，无功裕度最低的母线被认为是关键母线。电压稳定性指标在找出电压崩溃状况方面发挥了重要作用，指数V/V0，Lmn，VCI，FVSI和VCPI针对在不同负载条件下配置PMU的总线计算，可以用来评估系统电压稳定性，指数值介于0（正常情况）到1（电压崩溃）之间，显示了总线的临界状态。为了找出PMU 的配置位置，使用贪心算法满足PMU的最优配置位置，该算法找到具有最大连接性的总线以配置PMU。使用基于非线性迭代方法的WLS 方法进行状态估计，考虑到其为非线性估计，所提出的使用状态估计直接测量PMU的方法进行线性估计，不需要任何迭代方法。该方法形成一个矩阵，直接测量状态并计算其线性估计，它不仅提供了定位母线的电压，还有助于通过使用线路电流的方式间接计算相邻母线。