融合式翼梢小翼对飞机尾涡演化的影响
何昕,赵瑞,王琴,苑长江
(中国民用航空飞行学院空中交通管理学院,广汉 618307)
尾流是指飞机飞行过程中在翼尖产生的一对反向旋转的强烈湍流,是影响航空运行安全和效率的主要因素之一。飞机尾流特性、探测和演化趋势已经成为当前民航空中交通管制领域关注的前沿科学问题[1]。中国现行的飞机尾流间隔标准是20世纪70年代国际民用航空组织(International Civil Aviation Organization,ICAO)根据飞机最大起飞重量规定的相邻两架飞机运行的最小安全距离,但这个间隔值对于日渐增长的航空器运行量来说相对保守[2]。2013年,ICAO开展的航空系统组块升级(aviation system block upgrade,ASBU)中模块B0-WAKE计划修订ICAO现有的最低间隔标准[3]。同年,ICAO将尾流重新分类(recategorization of aircraft wake turbulence,RECAT)分为了3个阶段:航空器重新分类、细化静态尾流等级分类和构建动态尾流标准[4]。目前大部分国家已经完成前两个阶段,对于动态尾流标准国内外学者正在积极探索研究。2015年中国民航局拟定了航空器尾流再分类标准RECAT-CN[5]。2019年,RECAT-CN实验于广州和深圳试运行,参与实验的飞机占两场飞机总数的50%左右,实现尾流间隔平均缩减率约20%,运行效率大幅提升。2021年,RECAT-CN于北京、南京、成都等12个机场推广运行。RECAT-CN实验的核心思想是通过对不同机型重新进行精细化的分类,缩短前后机之间的尾流间隔,从而实现中国空域资源的高效利用。
决定尾流间隔的主要因素是尾涡强度,而尾涡主要产生在翼尖位置,在翼尖安装翼梢小翼可以阻挡下翼面气流经过翼尖位置向上翼面流动,减小机翼外段的尾涡脱落,从而实现减小尾涡强度的效果。目前民航客机安装的翼梢装置大多为融合式翼梢小翼[6]。融合式翼梢小翼可以实现机翼到小翼的光滑过度,减小机翼和小翼之间的气动干扰,增加翼尖抗弯和抗扭的强度。同时,飞机尾涡演化和消散受到气象环境参数(大气湍流耗散率、大气层结稳定度、风速等)的影响。中国现行的尾流间隔标准是在尾流不易消散的气象环境参数下制定的[7],缺乏一定的动态性。因此,研究不同气象环境参数下翼梢小翼对尾涡演化的影响能够为尾流间隔动态化、精细化发展提供一定的理论参考。
目前,尾涡演化的研究方法大致分为实验室风洞和水洞试验,现场雷达传感器观测和计算流体力学(computational fluid dynamics,CFD)3种方法[8]。其中CFD是最为简单高效的方法,中外学者利用CFD中的不同湍流模型对有无翼尖小翼的飞机进行了大量的研究。
Mahmood等[9]利用Spalart-Allmaras湍流模型对亚音速巡航飞行条件下有无翼梢小翼的直矩形机翼进行模拟,发现有小翼的机翼模型可以提供更高的升力系数、升阻比和更低的阻力系数;Seshaiah等[10]通过数值模拟得到融合小翼可以提高飞机的升阻比,提高飞气动性能;Ali等[11]通过SSTk-ω湍流模型计算对比分析了融合式翼梢小翼和螺旋式翼梢小翼的升力系数、阻力系数、俯仰和弯矩系数等气动参数,发现装有融合式翼梢小翼的飞机在飞行过程中飞行姿态更加稳定。
王丹等[12]利用雷诺平均 N-S方程(Navier-Stokes)计算了融合式、双叉弯刀式翼梢小翼的气动参数,分析了各参数对气动性能的影响;钱宇等[13]利用SST模型对未安装翼梢小翼和安装不同角度翼梢小翼的飞机进行了数值模拟研究,得到了安装合适角度的小翼可以减小尾涡危害,提升民航运行效率;张礼等[14]针对常规布局类客机,通过k-ω湍流模型数值模拟的结果,发现安装翼梢小翼后诱导阻力减小、客机巡航因子增大、巡航效能改善。
虽然中外学者在翼梢小翼方面进行了大量的研究,但这些研究的重点聚焦在翼梢小翼对飞机压力系数、升力系数、阻力系数和升阻比等气动参数上,关于翼梢小翼对尾涡演化的影响并未重点分析。翼梢小翼具有减少飞机油耗、提高运营经济性的优点,如今各航空公司选择对大部分飞机加装融合式翼梢小翼,因此研究融合式翼梢小翼对飞机尾涡演化的影响对空管领域实现尾流间隔精细化、动态化发展是十分重要的。
现根据雷诺平均 N-S方程(reynolds averaged navier stokes equations,RANS)数值模拟方法,采用SSTk-ω湍流模型对B737-800有无融合式翼梢小翼的机翼进行数值模拟计算,重点分析翼梢小翼在飞机尾涡演化过程中对尾涡速度、尾涡强度的影响。利用APA模型(AVOSS prediction algorithm)计算不同气象环境参数下小翼对尾涡消散的影响,以期为尾流间隔缩减提供更加精细化、动态化的理论支持。
1 尾涡数值模拟方法
1.1 几何模型和网格划分
通过Catia软件建立B737-800基本机翼和有融合式翼梢小翼机翼的模型,基本机翼翼展为34.31 m,如图1(a)所示,有小翼的翼展为35.79 m,如图1(b)所示。
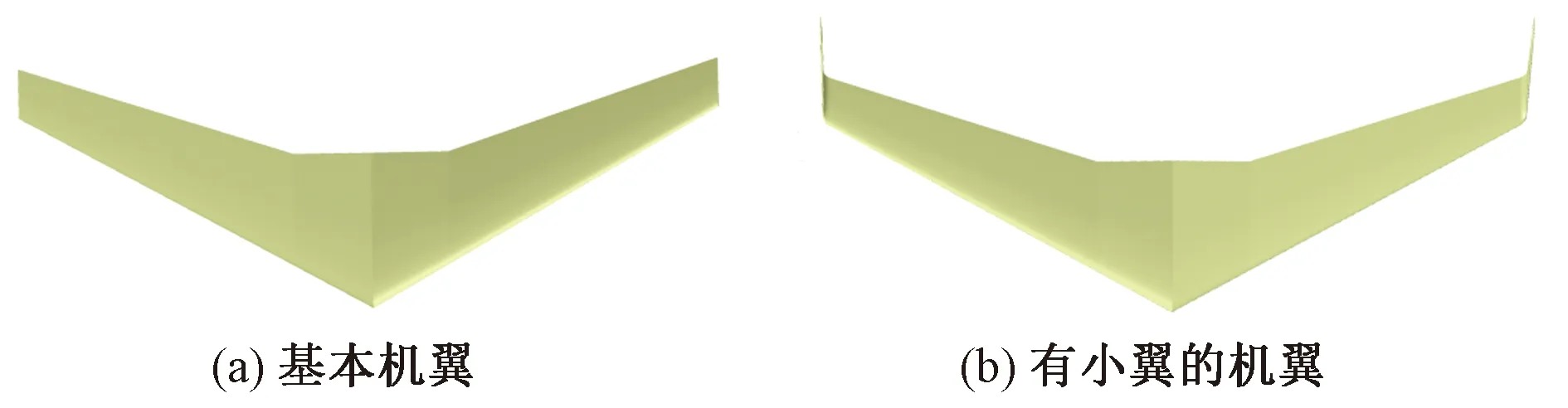
图1 机翼模型
建立2 500 m×600 m×200 m的六面体流场计算域,如图2所示,模型坐标原点为机翼最后缘点,x轴为翼展方向,y轴为翼弦方向,z轴的正方向为升力方向。
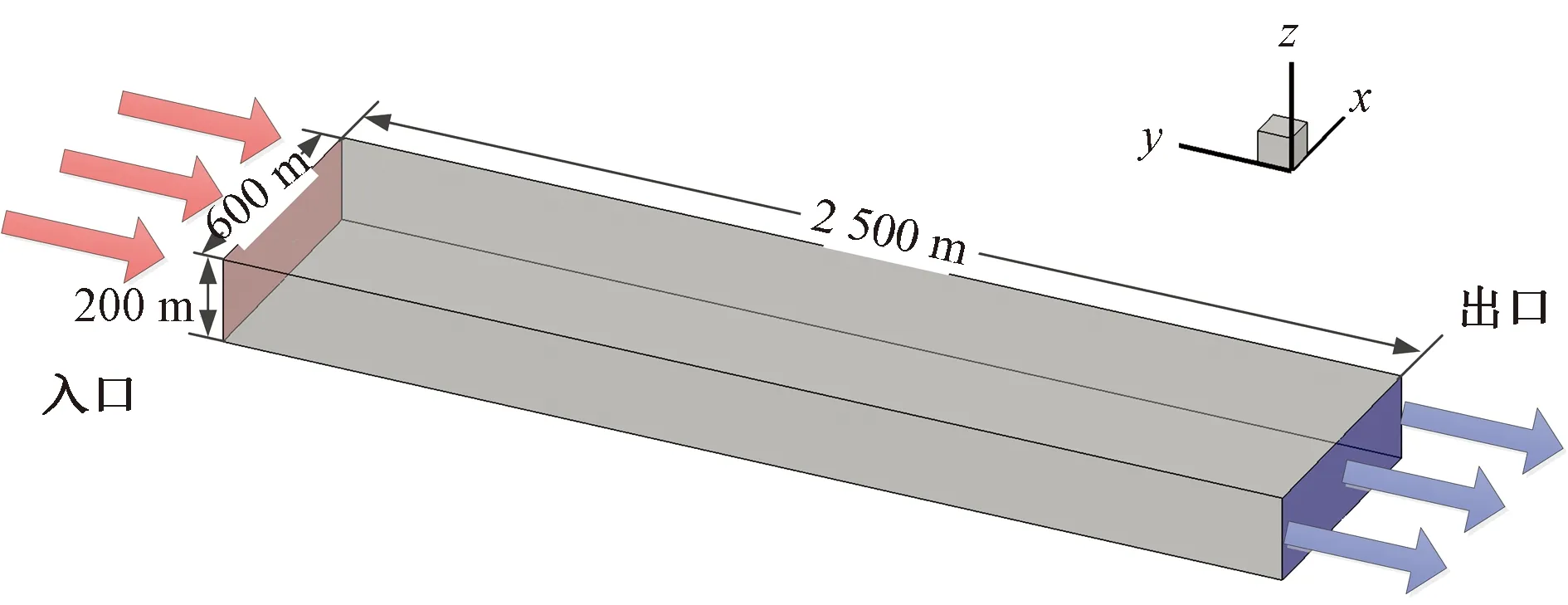
图2 流场计算域示意图
为提高计算效率增强计算稳定性,本文采用精度较高的结构化六面体网格。利用O-block加密了机翼周围的网格密度,增大机翼周围网格的正交性。最终流场区域和机翼的具体网格分布如图3所示。
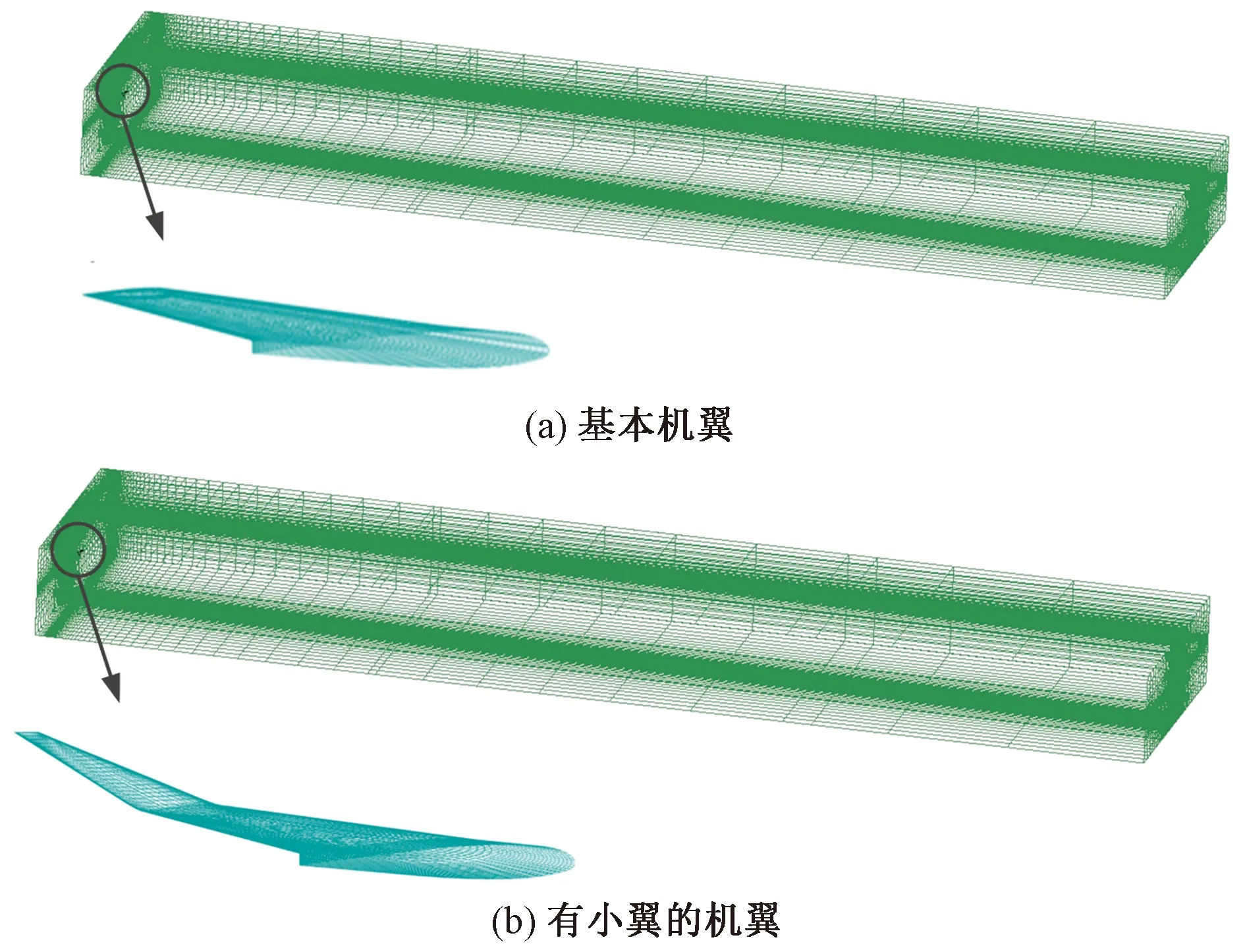
图3 网格分布图
1.2 数值模拟方法
1.2.1 控制方程
本文研究采用RANS方法,分析尾涡演化过程。RANS方法的基本思想是分解湍流流动,分解满足动力学瞬时N-S方程的变量为平均动量和脉动动量。将速度分量和压力分量、能量分量等代入瞬时连续方程和动量方程,获得笛卡尔坐标系下的N-S方程。
连续方程和动量方程的表达式为
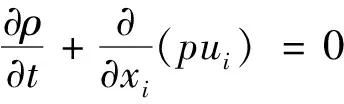
(1)
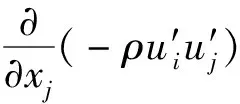
(2)
式中:ρ为大气湍流密度;ui为xi方向平均速度分量;uj为xj方向平均速度分量;p为大气压强;u′i、u′j为雷诺方程的应力项;σij为应力张量分量。
1.2.2 湍流模型
湍流模型选取SSTk-ω湍流模型,该模型的基本思想是:近壁处采用k-ω模型,边界层边缘和自由剪切层用k-ε模型,因此SSTk-ω具有k-ω模型和k-ε模型的优点[15-16]。SSTk-ω模型中的k和ω分别代表湍动动能和湍动耗散率,k和ω的运输方程为
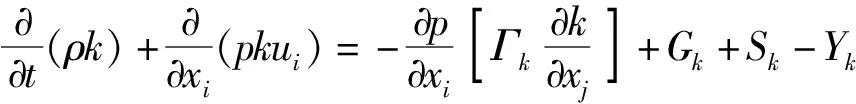
(3)
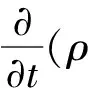
(4)
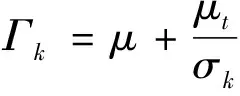
(5)
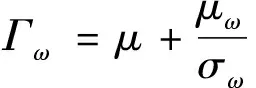
(6)
式中:μ为湍流黏性;Γk和Γω为扩散率;Gk和Gω为湍流动能;Sk、Sω为自定义内容;Yω、Yk为扩散产生的湍流;Dω为正交发散项;σk、σω为湍流能量特朗普系数。
1.2.3 边界条件
整个计算域为六面体的构型,流场入口设置为速度入口(velocity-inlet),出口设置为压力出口(pressure-outlet),壁面选择无滑移固壁面。根据B737-800的进场和离场情况,设置温度为288.15 K,大气压力为101 325 Pa,来流速度为68 m/s,马赫数为0.2。
2 数值模拟结果分析
2.1 翼梢小翼对尾涡速度的影响
从图4可以看出左右机翼末端的气流速度方向相反且呈漩涡状分布,机翼外侧的气流向上运动,机翼内侧的气流向下运动,并且尾涡速度流线有向下扩散的趋势。以上现象说明由于机翼左右尾涡之间存在诱导作用和尾涡本身的重力作用导致尾涡向下扩散并且减弱。
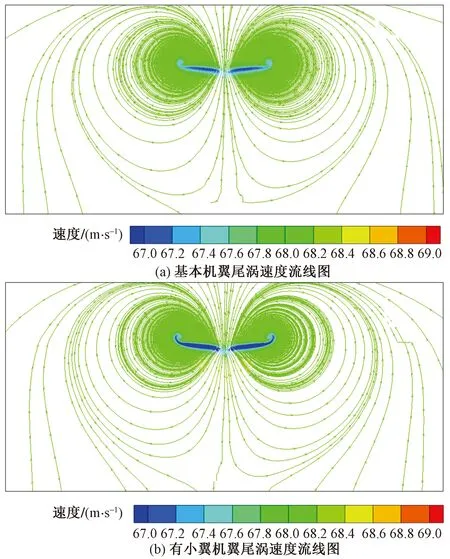
Y/b=i代表距机翼后i个翼展的距离
由图5(a)和图5(b)对比可知有翼梢小翼机翼的涡核速度比基本机翼的涡核速度更小,说明小翼导致涡核能量减小,涡核消散速度加快。有小翼机翼的速度等值线比基本机翼的速度等值线密集,说明小翼导致尾涡速度梯度增大,尤其是涡核周围的速度梯度。

图5 尾涡速度分布对比图
2.2 翼梢小翼对尾涡强度的影响
飞机尾涡速度环量是用来表示尾涡强度的一种特征参数,环量是指速度沿着一条封闭曲线的线积分[17]。在理想气体中,飞机的尾涡环量应该处处保持不变且相等,但在飞机实际飞行中由于空气黏性的存在,气流逐渐靠近涡核中心,速度梯度增加,气流黏性增大,尾涡环量减小,直到涡中心尾涡环量衰减到零。
由2.1节中得到两种机翼的速度梯度对比结果可知,有小翼的机翼整体尾涡速度梯度更大,导致尾涡周围空气黏性增大,尾涡环量更小,尾涡环量更快衰减到零。
从图6(a)可知,基本机翼左右翼尖涡量相反说明左右翼尖形成了一对方向相反的漩涡,从图6(b)可以看出有融合式翼梢小翼的机翼主翼涡被分割成两个方向相同的涡,分别产生在小翼末端和主翼末端。小翼涡和主翼涡强度相当并且方向相同,当两个涡靠的足够近时,受到外界因素的干扰,小翼涡和主翼涡逐渐融合成一个大的涡旋,从而降低能量集中程度、减小尾涡强度。当尾涡发展到机翼后缘6个翼展左右的位置时小翼涡和主翼涡已经完全融合,形成一个翼尖涡,如图7所示。融合后的翼尖涡量小于基本机翼翼尖涡涡量,如图8所示。
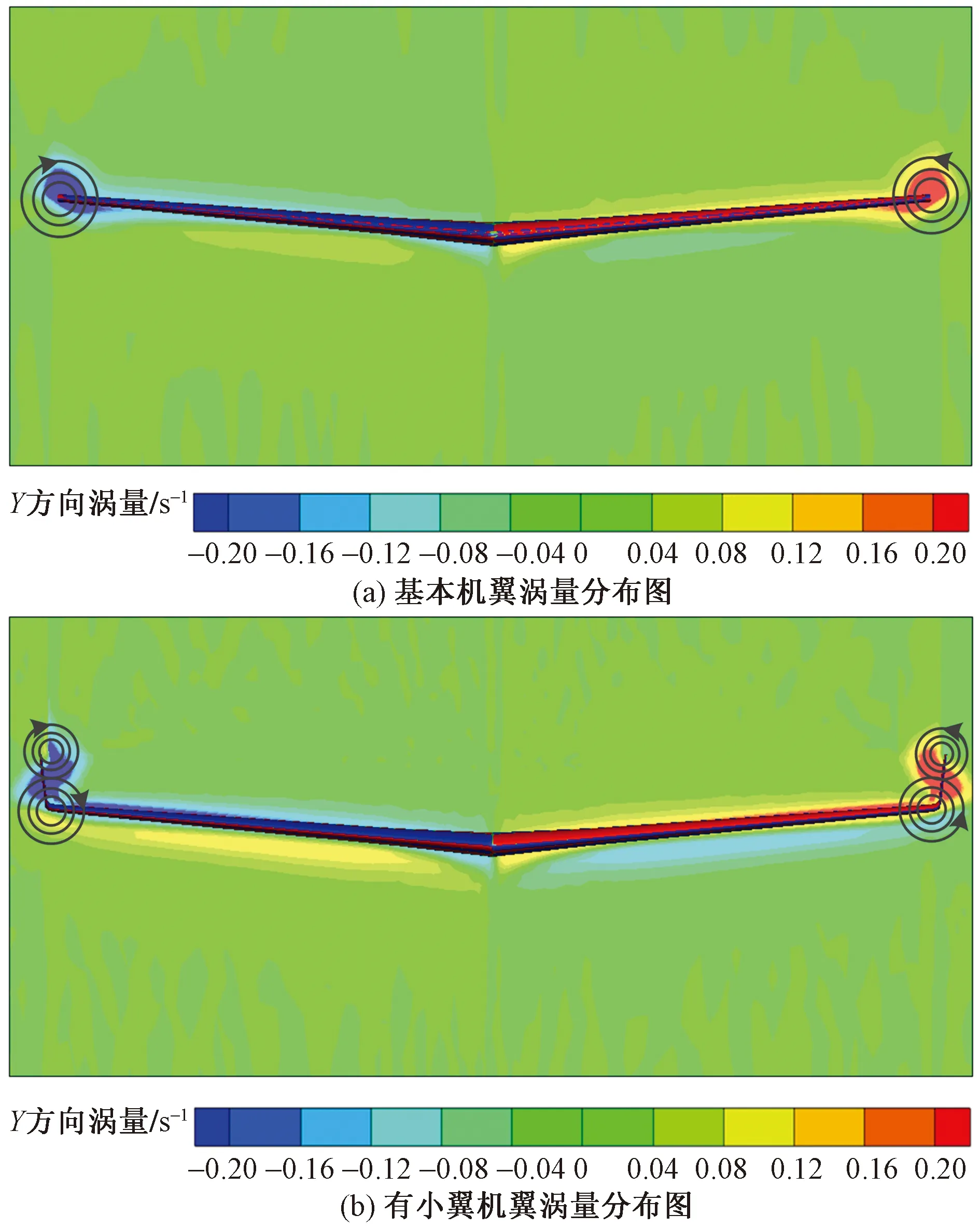
图6 Y/b=1处涡量分布对比图
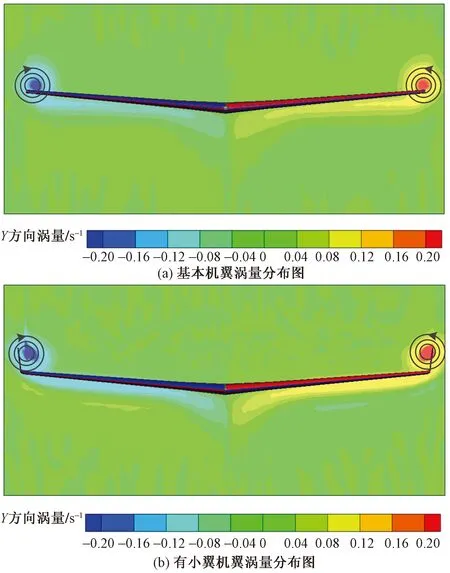
图7 Y/b=6处涡量分布对比图
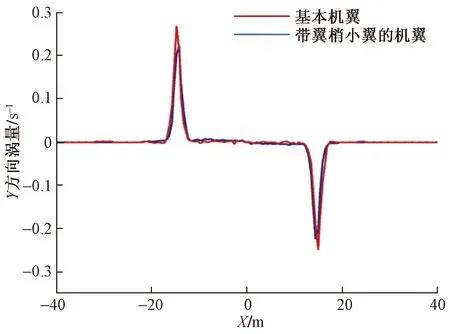
图8 Y/b=6处涡量对比图
3 APA尾涡消散模型分析
通过数值模拟获得有无小翼的尾涡速度和强度的变化,下文将通过尾涡消散模型APA模型对有无小翼机翼的尾涡消散进行进一步研究验证。
APA尾涡模型可以准确地预测尾涡消散行为,并且该模型已经成功应用在NASA的动态尾流间隔系统(aircraft vortex spacing system,AVOSS)中[18]。APA消散模型将尾涡消散过程分成两个阶段:近场阶段和远场阶段,近场阶段是从飞机后大约6个翼展的距离,尾涡环量基本不变[19],衰减模型如式(7)所示,远场阶段的尾涡环量衰减的速度会突然加快,衰减模型如式(8)[20]所示。
Γ(t)=Γ0{1.1-10[-5t0/(t+5t0)]}
(7)
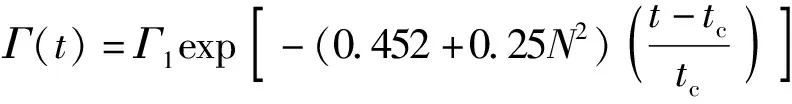
(8)
近场阶段发展到远场阶段的时间即尾涡开始消散时间的计算方法[21]为。
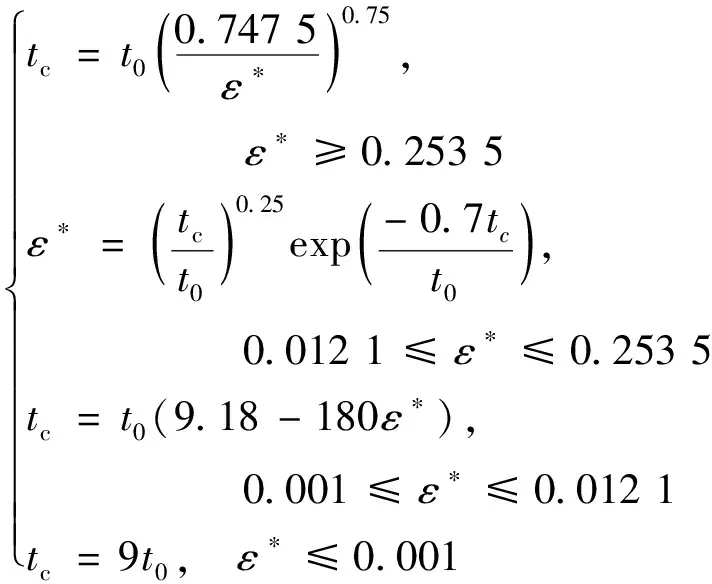
(9)
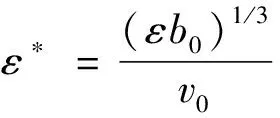
(10)
式中:Γ0为初始尾涡环量;Γ1为近场涡发展到远场涡时的尾涡环量;tc为无因次开始消散时间;t0为参考时间;b0为左右涡间距;ε为大气湍流耗散率(eddy dissipation rate,EDR);ε*为尾涡耗散率;N为浮力频率(Brunt-Vaisala frequency)。
EDR算法是世界公认的最先进的,颠簸算法之一,2018年ICAO附件3[22]中表明:颠簸情况必须根据EDR的立方根值(ε1/3)报告。同年,厦航已经掌握了EDR相关技术并积极建立EDR数据共享平台。基于此,根据式(9)和(10)选取ε*=0.001、0.01、0.15、0.26的情况,计算得到ε1/3=0.000 5、0.005 2、0.077 7、0.134 7,有小翼机翼的ε1/3=0.000 6、0.005 7、0.085 8、0.148 6,其中ε1/3=0.134 7和0.148 6对应轻度颠簸,其余值对应无颠簸。浮力频率N是指流体质点受到扰动后,在重力和浮力共同作用下使其恢复到原来位置时产生的振荡频率,表示大气分层效应即大气层结的稳定度[23]。
利用APA模型计算不同尾涡耗散率和不同浮力频率下基本机翼和有翼梢小翼机翼的尾涡消散情况,计算结果如图9所示。
从图9中可以看出尾涡消散过程分为两个阶段,近场阶段(Y=0b~6b)尾涡消散速度曲线较为平缓消散较慢,远场阶段曲线斜率较大,尾涡消散速度加快。
从图9中可以发现两种机翼尾涡消散的共同规律:随着大气湍流耗散率和大气层结稳定度的增大,远场尾涡消散速率加快。但两种机翼对尾涡消散又有不同的影响。近场阶段有翼梢小翼机翼的尾涡强度比基本机翼的尾涡强度有所减小,远场阶段小翼对尾涡强度的影响程度并不大,并且随着时间的增大影响程度逐渐减小。当N=0时,大气湍流耗散率越大,小翼对远场涡的影响随时间的增大而减小。当N≥0.5时小翼对远场涡的影响就变得微弱,尤其是N=1时即发生轻微颠簸时小翼对远场涡的影响十分微小。当大气耗散率一定时,大气层结越稳定即N值越大,小翼对远场涡的影响越小。
4 结论
应用RANS方法对基本机翼和带翼梢小翼的机翼进行了数值模拟分析,并利用APA消散模型对两种机翼的尾涡强度对进行了对比计算。
(1)对比分析两种机翼产生的尾涡速度后发现,B737-800有融合式翼梢小翼的机翼产生的尾涡速度减小、能量减小、尾涡速度梯度增大。
(2)根据速度梯度的变化可知有小翼机翼的尾涡环量减小。同时,小翼将翼尖涡分割成两个方向相同的涡,两个涡相互影响从而减小尾涡强度,降低了前机对后机的影响。
(3)根据APA尾涡消散模型计算发现小翼会减小近场尾涡的强度,但对远场尾涡强度的影响并不大。不同大气湍流耗散率和大气层结稳定度下,安装小翼对尾涡强度的减小量不同。

