基于验证集辅助的脑电信号包裹式降维

张杰,曲洪权*,柳长安,庞丽萍

(1.北方工业大学信息学院,北京 100144; 2.北京航空航天大学航空科学与工程学院,北京 100191)

随着当今社会科技发展,体力作业逐渐被劳动者交给工业机器完成,人机交互作业比重增长迅速,脑力劳动的重要性逐年递增,由此导致工作中劳动者脑力负荷越来越高[1]。脑力负荷并非单一概念,它涉及课业的需要、时间上带来的压力、执行者的能力、操作者临场的表现等多维因素,判断起来较为复杂,因而多数研究者将其看作为劳动者在单位时间内的脑活动量、心理压力或信息处理能力[2]。在人机交互作业中,大量需要处理的信息使得操作者脑力负荷呈较高状态,尤其在高空领域等环境复杂且待处理信息繁杂、操作精准度要求极高的情况下,随着操作者亟待处理的信息量的增加,操作者脑力负荷状态相比以往也不可同日而语,甚至会出现超负荷状态。有研究表明,脑力负荷过低会导致人力资源的浪费,使得工作效率不高,脑力负荷过高则会导致失误频出,在高空作业等领域甚至会引发严重事故[3]。因此,对脑力负荷进行实时、准确的评估,并依照评估调整操作者的工作顺序和工作量,在当下有着十分重大的意义。

现今脑力负荷评估方式主要有3种,分为主观评估量表、绩效指标和生理指标[4]。3种方法各有利弊,然而为实现对脑力负荷实时、客观的评估,经大量研究证明,生理指标显然要优于其余2种。在各类生物电指标中,脑电信号与脑力负荷的相关性更高,且近期有研究表明,功率谱密度这一特征提取方法十分适用于脑电信号,可以较为客观准确地量化生理信号[5],因而本次课题选取脑电信号进行脑力负荷分类研究。

此外,脑电信号通道过多导致特征维数较高,极易造成维数灾难[6],导致所需训练集十分庞大,且训练量曾几何倍数增长。现今应用最广泛的降维方式为主成分分析(principal components analysis,PCA)[7],但主成分分析本身是提取最佳描述特征的降维算法[8],针对本课题的分类问题,效果并不显著。

基于此,现提出一种基于PCA-SVM与逐阶枚举法的包裹式降维方式,在支持向量机(support vector machine,SVM)交叉验证的基础上,引入固定验证集概念,通过监督特征选择过程来弥补PCA非监督降维方法在分类上的劣势,通过逐阶枚举法来避免SVM算法本身对特征之间关系的敏感性所导致的特征选择偏差,以此找到针对分类更为有效的降维方式。

1 脑电数据采集及预处理

本次实验共选取8位被试者,均为身体状况良好的研究生,每天上、下午各测一次,每次获得高低负荷脑电信号数据各12 min,实验数据收集横跨9 d时间,获得各被试高低负荷不同情况下每种情况各216 min脑电信号。实验平台为MATB-Ⅱ,如图1所示。

图1 MATB-Ⅱ实验平台

由于获取脑电数据时使用的是32-channel Neuroscan Neuamps (Synamps2,Scan4.3,EI Paso,USA) system获取的脑电数据,而在使用蒙太奇进行电极通道传感器配置时使用的是10-20系统电极放置法(国际脑电图学会标准电极放置法)。因此选取32-channel Neuroscan Neuamps system和10-20系统电极放置法中能一一对应的26个电极脑电数据:FP1、FP2、F7、F3、FZ、F4、F8、FC3、FCZ、FC4、T7、C3、CZ、C4、T8、CP3、CPZ、CP4、P7、P3、PZ、P4、P8、O1、OZ、O2作为26个独立分量,用于后续特征提取工作。脑电提取与电极排布示意图如图2所示。

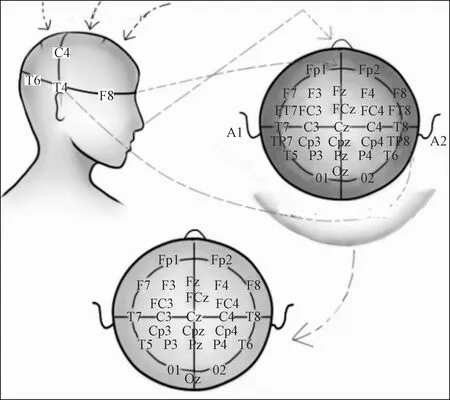
图2 脑电提取与电极排布示意图

在预处理过程中,如图3所示,首先将采集到的数据通过fir带通滤波器,进行1～30 Hz的滤波处理,按照单个任务时长0.5 min进行切割,用于后续特征提取。

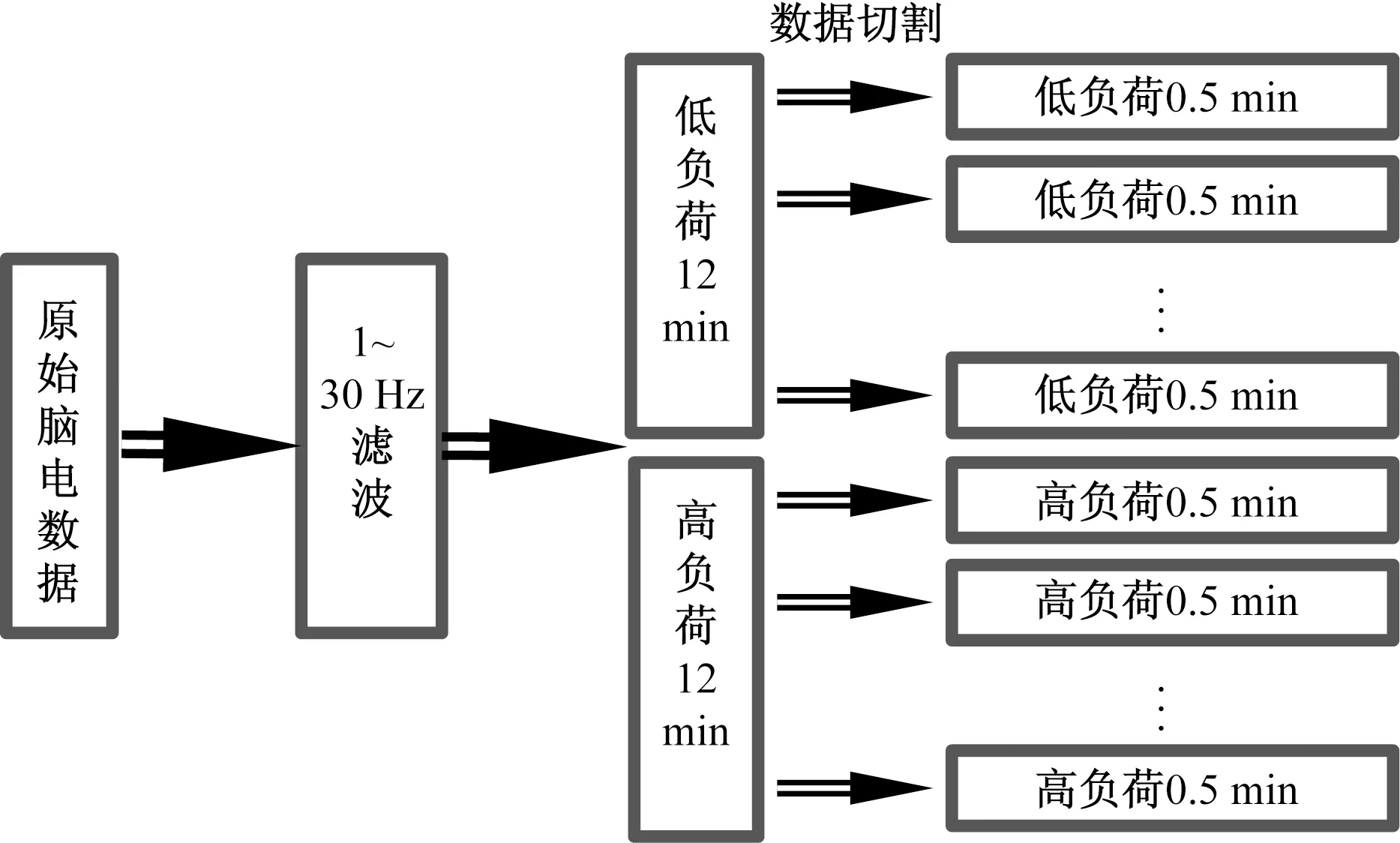
图3 数据预处理过程

2 脑电信号特征提取

针对经过预处理的脑电信号数据进行特征参数值的提取,目前常用方式有4种,即小波变换、共空间模式、AR模型,以及功率谱密度[9]。有研究表明,功率谱密度这一方式在脑力负荷分类任务上更为适用[5]。

通过大量研究表明,在脑电信号的研究过程中,已知有至少4个波段对研究结果影响较大,即delta、theta、alpha、beta 4种节律[10],具体波段划分如表1所示。

表1 具体波段划分

功率谱密度属于频域法,指利用密度概念来表示信号在每个频率点的功率分布的方法[11]。首先对脑电信号做傅里叶变换,具体步骤如下。

将每个通道作为一个独立分量(ICs),对于经过预处理的脑电信号,每2 s划分一个epoch。设每个ICs生成了M个epoch,进行多窗谱法处理(multitaper)时共有N个采样点,则电极通道ch第m个时长为2 s的epoch使用multitaper在第n个采样点处计算得到的PSD值记作PSDch,m,n。其中,ch=1,2,…,26,m=0,1,…M-1。

则通道ch中ICs平均一个epoch在第n个采样点处的PSD值,即

(1)

根据频率分辨率对各通道ch每个采样点处的绝对PSD值进行归一化,得到相对PSD值为

(2)

在不同节律频率区间下,对应着不同的采样点。

以alpha节律为例,将alpha节律下的采样点范围记作n_alpha～N_alpha,则alpha节律下各电极通道总的平均相对PSD值为

(3)

根据式(3)分别提取4种节律下26通道的平均功率谱密度,得到104个特征。

3 基于验证集辅助的脑电信号包裹式降维方法

为脑力负荷分类研究,提出了一种基于PCA-SVM与逐阶枚举法的降维方式,以测试集分类精度为指标,经数据预处理、特征工程、训练分类器三部分,大体流程如图4所示。

特征工程阶段主要包括3步,即脑电信号特征提取、特征降维、特征选择,依照以往大量研究,本文研究使用平均功率谱密度作为特征提取方式,主要研究特征降维、特征选择两方案的制定方式。

3.1 PCA-SVM包裹式特征降维

所使用脑电数据26通道,每通道4种节律,经过特征提取后,总和共104个特征维度,极其容易造成特征冗余,从而引发维度灾难,因而需要使用降维方法尽可能地降低维度。主成分分析是目前使用最为广泛的一种降维方式,其目的是在尽可能多保留信息的基础上,使用低维空间以表示高维数据。

具体来讲,PCA方法其实是将原始特征空间中的数据映射到另一空间中,使第一个新坐标轴方向为原始数据中方差最大的方向,第二个坐标轴方向为与第一个坐标轴方向正交且使其方差最大的方向,依次类推,重新构建特征空间[12]。

由此可知,主成分分析本身是一种非监督降维的方式,所保留的特征是基于其累计贡献率,因此这种方法对于分类而言并不完全适用。

如图5所示,以sub01为例,测试集精度并不完全与累计贡献率成正比,且随维度变化较反复,也就是说,按照主成分分析方法将原始数据映射到新特征空间后所保留的特征维度,只是数据的最佳描述特征,而并非着眼于数据可分性,且过度依赖于训练集。

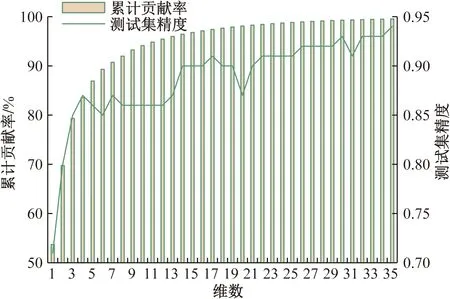
图5 sub01特征累计贡献率与测试集精度随PCA维度变化情况

为解决此类问题,本文研究采用包裹式的降维方式,将PCA与分类器结合,在尽可能保留更多信息量的同时增大数据可分性。与其余特征选择方式不同,传统意义上的包裹式降维方式就是直接把最终将要使用的学习器的性能作为特征子集的评价准则,也就是说,其目的就是为给定学习器选择最有利于其性能、量身定做的特征子集,直接针对给定学习器进行优化[13]。

本文所提出的方法则是将分类器与PCA结合,并非直接优化学习器,而是针对在特定学习器下的数据可分性,在训练集中分出固定验证集,根据验证集精度针对特征工程方案进行优化。由于包裹式在降维过程中将最终使用的学习器纳入考量,在一定程度上完善了PCA的分类性能。

基于支持向量机(SVM)的高效准确性,本文研究选用SVM作为分类算法,并根据上述所说,组成PCA-SVM包裹式特征选择算法进行特征工程阶段的处理。

实验分别使用各被试跨时间数据,总目的为将数据降至m维,本阶段目的则为将数据降至n维,具体流程图6所示。具体流程如下。

步骤1首先对通过预处理的数据进行平均功率谱密度计算,每个任务皆提取到26×4个特征维度。

步骤2将数据按8∶2分为训练集和测试集,再将训练集按8∶2分为特征训练集和特征验证集。

步骤3对特征训练集使用主成分分析(PCA)分别降至[m,40]维,生成40-m个子集。依靠SVM生成各子集相对应的模型,并输出该模型特征验证集精度,确定精度最高的维度n,保留当前子集,并输出降维矩阵。

3.2 逐阶枚举特征选择

支持向量机(SVM)是目前运用最广泛的机器学习分类器,中心思想为最小间隔最大化。该方法适用于二元分类的任务,且对于特征之间相应关系较为敏感,有时会出现特征之间相互不适配导致整体分类效果降低的情况[14]。

为进一步降低SVM训练分类器阶段上述情况发生的可能性,特征降维阶段过后,在PCA-SVM包裹式选择的基础上,提出了一种逐阶枚举法,并将其引入特征选择阶段,以此增强数据在SVM学习器下的可分性。此法大体来讲即为逐阶进行特征选择,每层选择特征总数-1个特征,相较于穷举法避免了大量运算,并有效聚焦于各特征间的适配性,在SVM学习器下更接近于特征最优选择。

实验分别使用各被试跨时间数据,目的为将数据降至m维,具体流程如图6所示。

步骤1对于上一步所确定的n个特征维度,固定前面5个信息量最大的维度确保其不被删除,对降至n维的数据使用逐阶枚举法进行特征选择,枚举其n～1个特征组合的n～5个子集,依靠SVM分别生成模型,输出该模型特征验证集精度,保留精度最高的子集,记录删除特征的位置。

步骤2重复步骤1,直到将特征维度降至m维,输出删除特征位置集合。

当m=20时,具体流程如图7所示。

图7 特征选择阶段具体流程

完成以上两步后,可得到脑电数据的降维参数。根据PCA-SVM法输出的降维矩阵与逐阶枚举法所输出的删除特征位置集合,对训练集与测试集进行处理,使用处理过后的训练集数据依靠SVM算法生成模型,并使用处理过后的测试集数据进行测试,可输出测试集精度。

在特征工程阶段引入了固定验证集概念辅助进行包裹式降维,以特征验证集精度作为特征工程方案的评价标准,并在特征选择中使用了逐阶枚举法,可以将数据降至任意维度。

4 脑力负荷分类实验结果与分析

每组实验分别使用各被试跨时间数据,每种负荷情况各216 min,经数据预处理后,每被试各有数据段864个。支持向量机核函数选择高斯核,为在保持训练速度的基础上尽量避免过拟合,使用3折交叉验证法,并使用网格寻优法确定参数。对每被试数据按照上述3种方式进行训练与测试,实验结果如图8所示。

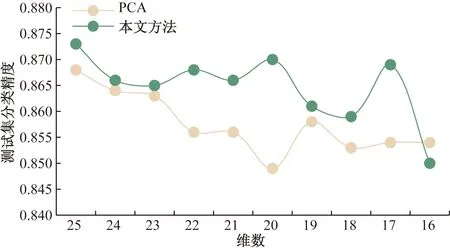
图8 两种方法测试集精度均值随维度变化折线图

以维度为自变量,分别按照3种方法训练SVM分类器,取8个被试的平均值绘制折线图,结果如折线图8所示。由图8可知,两种方法测试集精度均随维数降低有一定下降,然而本文所提出的方法在特征数高于16维时普遍好于PCA方法,其中降至20维时此方法效果更为显著。

由于降至20维时该方案效果较为显著,于是以20维为例,统计8个被试在分别使用两种方法降维时的测试集精度,结果如表2所示。

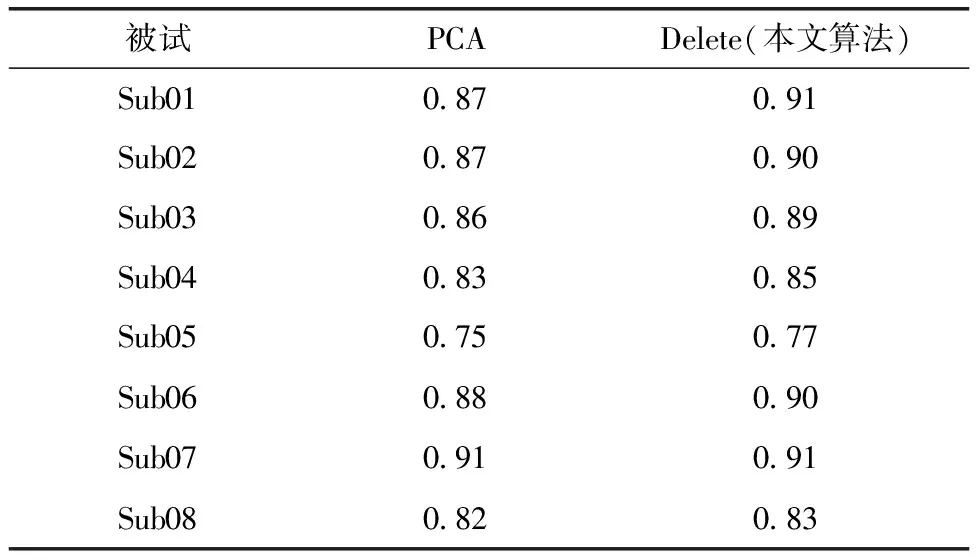
表2 各被试分别使用两种方法所得测试集精度

为更为直观地感受变化,将表2用直方图进行可视化,效果如图9所示。由此可知,当数据降至20维时,除sub07高精度持平外,各被试测试集精度相比单纯使用PCA均有不同程度升高。

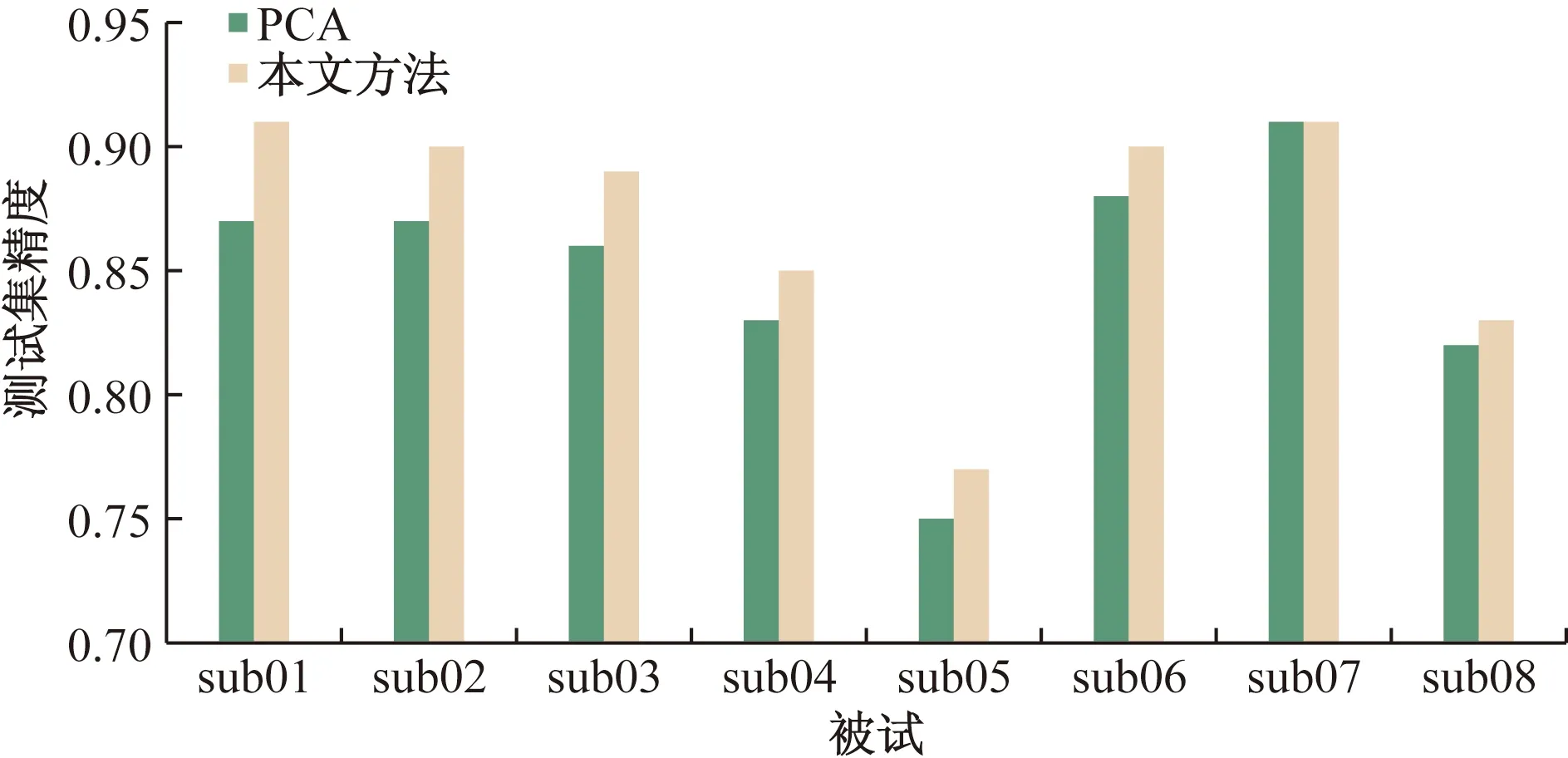
图9 各被试两种方法降至20维测试集精度对比柱状图

5 结论

对于脑电信号,针对非监督降维和SVM分类算法的特性,提出了一种基于PCA-SVM与逐阶枚举法的降维方式,通过实验结果可以看出,此方法在一定程度上缓解了PCA由于其非监督算法着重于信息最大化的性质所一并带来的对数据可分性的破坏,具体总结如下。

(1)引入了固定的验证集概念,在特征工程阶段代替全部训练集调整参数,避免了特征工程方案过度拟合训练集。

(2)在特征工程阶段加入支持向量机,进行包裹式降维,一定程度上弥补了非监督降维算法在数据可分性上的牺牲。

(3)对于全举法而言,逐阶枚举法也在接近于特征选择最优组合的前提下降低了训练量。

因而本文提出的逐阶枚举法对于较为注重特征之间关系的SVM分类器适配性更高,一定程度上解决了子空间分类效果高于整体分类效果的问题,也为生物电信号的特征工程算法提供了新思路。