四边折弯机基于GNS 的多组龙门轴插补控制
黎兴宝,丁 宇,周 祥,马正平
(江苏亚威机床股份有限公司,江苏 扬州 225000)
0 引言
随着制造业的突飞猛进,各类大型机床的开发和应用也快速发展。为实现更加有效、更加稳定的设备控制,其核心部件大多采用龙门式结构[1]。随着龙门轴广泛应用,设备不论在机械刚性还是动作响应方面都能够更高程度地满足需求。本文主要论述在四边折弯机中运用固高GNS 控制器控制折边梁X轴和Z 轴完成龙门插补动作的过程。
1 固高GNS 控制器
GNS 运动控制器是以X86 架构的CPU 和芯片组为系统处理器,提供强大的计算和数据处理能力,采用高性能DSP 和FPGA 作为运动控制协处理器。可以实现高性能多轴协调运动控制和高速点位运动控制的同时,支持多轴运动控制,可用于运动控制系统,如CNC 机床、机器人、自动化生产线等,基于codesys 编程环境,提供灵活的开发环境和丰富的软件库,方便用户进行系统开发和定制化编程。
2 四边折弯机介绍
四边折弯机是一种用于对金属板材进行折弯加工的机器设备。它能够将平坦的金属板材通过多个步骤和工具进行弯曲,以实现所需的形状和角度。
四边折弯机通常由以下几个主要组件构成:
(1)机架。提供机器的结构支撑,保证稳定性和刚性;
(2)床板。用于固定和支撑金属板材,通常是平坦的工作表面;
(3)上、下模具。用于进行弯曲操作的工具。上模具固定在上横梁上,下模具固定在下横梁上,两者可以闭合和打开,以夹持和释放金属板材;
(4)按钮、脚踏板或数控面板。用于控制机器的操作和参数设置。不同型号的四边折弯机可能采用不同的控制方式。
四边折弯机的工作原理是通过上、下模具的运动将金属板材夹持,然后施加压力使其发生弯曲。通常,金属板材在机器上的定位由后挡料和夹具来完成。运用适当的力量和工具调整,四边折弯机能够完成较复杂的几何形状和角度要求。
四边折弯机在金属加工和制造行业中被广泛应用,用于生产各种类型的零件和产品,如金属箱体、槽型结构、护栏等。它可以实现高效的生产和一致的工艺质量,提高工作效率和生产效益。
3 四边折弯机折边梁结构
折边梁前后水平运动的轴称为X 轴,由X1和X2两台电机组成龙门,靠近压紧模具的方向为负,远离压紧模具的方向为正;折边梁上下垂直运动的轴称为Z 轴,由Z1和Z2两台电机组成龙门,向上为正方向,向下为负方向(如图1 所示)。
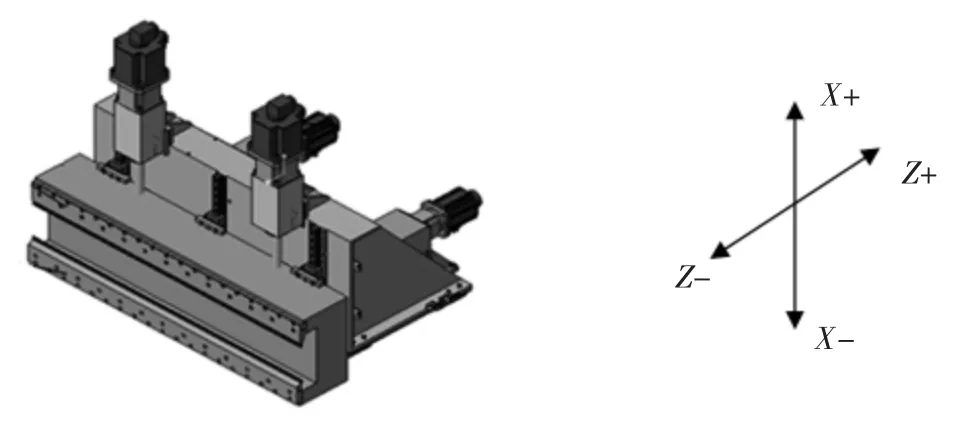
图1 折边梁运动轴
4 龙门轴介绍
龙门轴是一种常见的机床结构,通常用于数控加工和大型工件的加工。它由两根立柱(柱柄)和它们之间的横梁(称为横梁或龙门)组成。这种结构形似门框,因此得名为龙门轴。
龙门轴的主要特点包括:
(1)高刚性。龙门轴采用刚性框架结构,具有良好的稳定性和刚性,可以承受加工过程中的切削力和振动。
(2)大载荷能力。由于其框架结构的支持,龙门轴能够处理和加工大型工件,并能够承受较高的载荷。
(3)高精度。龙门轴的结构稳定,使其能够实现高精度的加工和定位,适用于精密加工要求。
(4)大型工作区域。龙门轴的设计使其具有较大的工作空间,可以容纳大型工件和进行复杂的加工操作。
(5)高效率。由于其刚性和稳定性,龙门轴可以实现高速加工,并提高生产效率。
(6)可扩展性。龙门轴可以根据需要进行定制和扩展,以适应不同尺寸和加工需求。
龙门轴常用于数控铣床、数控加工中心、龙门磨床等机床中,被广泛应用于航空航天、汽车制造、模具制造和重型机械制造等行业。
5 四边折弯机折边梁龙门轴设定
由上述机械结构可知,折边梁共两组龙门结构,系统通过对X 轴和Z 轴插补控制实现上下折边,龙门轴实现方式如下代码所示:
轴1 和轴2 组成X 轴,轴3 和轴4 组成Z 轴。
6 龙门轴插补
龙门轴插补是指在龙门轴系统中同时控制多个轴,实现复杂的运动轨迹插补。这种插补技术常用于数控机床中,用于控制丝杠、伺服电机或液压系统,使工具或工件沿着预定的曲线或路径进行精确的运动和加工。
龙门轴插补的实现通常基于控制系统中的数学模型和算法,将输入的加工参数转化为多轴控制指令,通过精确控制各轴的运动,实现期望的加工轨迹。
在龙门轴插补中,常用的插补方式包括:
(1)直线插补。控制龙门轴在直线路径上平滑地移动,用于直线加工和轮廓加工。
(2)圆弧插补。控制龙门轴在圆弧路径上运动,用于圆弧加工和弯曲轮廓的加工。
(3)螺旋插补。控制龙门轴在螺旋路径上旋转和移动,常用于螺纹加工和螺旋线加工。
在实际应用中,龙门轴插补常与数控系统和CAD/CAM软件相结合,通过将设计的零件轮廓或运动路径转化为插补指令,实现精确的加工过程。
龙门轴插补的实施需要结合具体的控制系统和机床参数,并根据加工需求进行调整和优化。专业的数控工程师和操作员通常负责选择适当的插补方法,并确保在加工过程中能够实现所需的精度和效率。
多组龙门轴可实现直线插补、圆弧插补、样条插补等多种不同类型插补动做,为了获得更好折边效果,本文研究中选取样条插补作为折边梁主要插补动作。
7 样条插补
为了确保折边粱动作更加平滑,需要确定各个轨迹点的位置、速度、各点间的运行时间,甚至还需要加速度。应对这种需求,控制器会设计样条插值(Cubic Spline Interpolation),相对于插值曲线函数规划,问题在于跟踪,因为规划的路径是理想的,但实际上电机运行受各种扰动的影响,如何很好地动态跟踪,达到设定目的才是关键。
B 样条多项式的一般形式可以表示为:P(X)=ΣNi(X)*Pi
其中,P(X)是B 样条曲线在参数X 处的值,Ni(X)是第i 个基函数,Pi是对应基函数的控制点。
常用的B 样条多项式包括:
(1)线性B 样条多项式(一次B 样条)用于插值和拟合直线段。
(2)二次B 样条多项式(二次B 样条)用于较光滑的曲线拟合。
(3)三次B 样条多项式(三次B 样条)用于更光滑的曲线和曲面建模。
经过三次多项式B 样条插补,原本直线段可拟合相对柔和圆弧,如图2 所示。
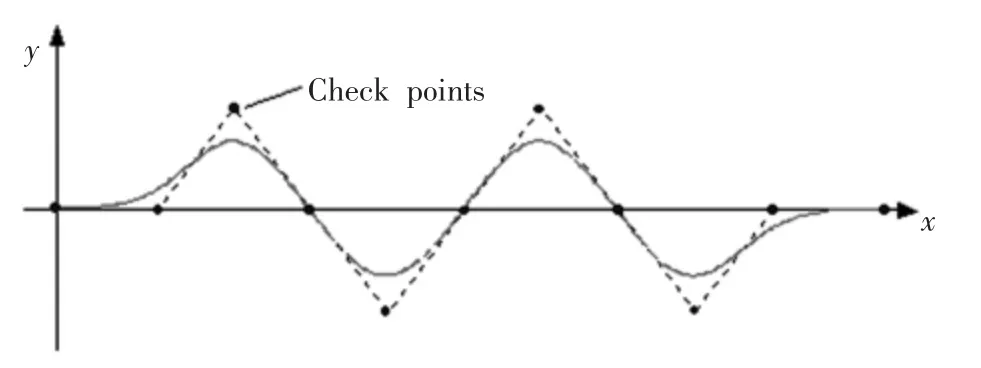
图2 插补拟合曲线
8 B 样条插补动作代码
这里我们假设多项式为:F(x)=ax3+bx2+cx+d,其中a、b、c、d 为实数。在OtoStudio 中代码实现如下所示。
在上述示例中,我们实现了一个名为FB_B_Spline 的函数,该函数使用三次B 样条多项式插值计算B 样条曲线上的点。函数接受参数值`X` 和一个包含控制点的数组。插值计算在区间(i,i+1)内进行,其中i 是整数。
通过调整a、b、c、d 四个参数值,通过Matlab 模拟仿真,拟合适合机械装置样条插补曲线,如图3所示。
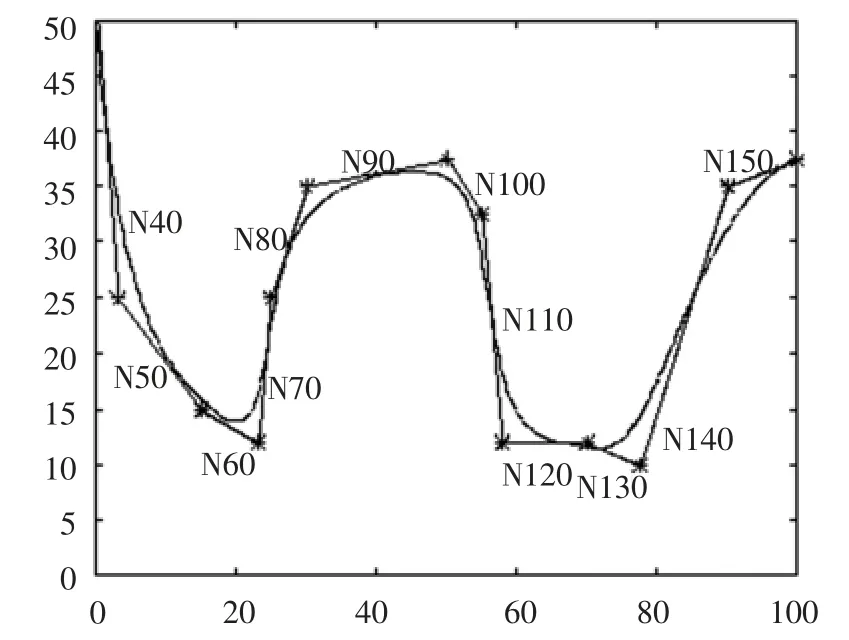
图3 仿真拟合曲线
9 结语
固高GNS 控制器,作为一款经济型嵌入式控制器,不仅在功能上可以同时满足多组龙门轴同时控制,同时也能利用PVT 算法拟合出最匹配机械装置的B 样条插补曲线,使得产品在性能最大化的同时,成本也得到了有效控制。

