基于并行计算的侧信道攻击加速方法*

苏 杨，季凡杰，许 森，王伟嘉，2，3

1.山东大学 网络空间安全学院，青岛266237

2.泉城省实验室，济南250103

3.山东大学 密码技术与信息安全教育部重点实验室，青岛266237

4.观源(上海) 科技有限公司，上海200241

1 引言

自1996 年Kocher 博士首次提出侧信道攻击以来[1]，侧信道攻击及其防御对策的研究已经逐渐成为密码学研究中的一个重要分支，受到了国际学术界与产业界的广泛关注.侧信道攻击不同于传统的密码安全，传统的密码安全通常假设攻击者最多能接触到密码算法的输入、输出和公开参数[2]，但是在现实中，攻击者往往可以观察到密码算法运行在具体软硬件上时泄漏的额外信息，如运行时间、功耗等，并利用这些信息对密码进行更有效的分析.这一类绕过密码算法本身繁琐的分析，而利用其运行过程泄漏信息的攻击方法称为侧信道攻击.

能量分析攻击是最重要、最有效的侧信道攻击形式之一[3]，这是一种非侵入式攻击，主要利用密码设备运行的物理特征而非密码算法的数学特性[4]进行攻击.能量分析攻击包括简单能量分析SPA (simple power analysis)、差分能量分析DPA(differential power analysis)[5]、相关性能量分析CPA(correlation power analysis) 等主流攻击方式.其中CPA 是一种利用功耗曲线执行侧信道分析的强大方法[6]，并且伴随着相关研究的进展，业界对CPA 的研究逐渐从攻击的准确性过渡到攻击时计算的有效性.

随着科学技术的飞速发展及计算机硬件水平的不断提升，计算机的性能也在不断提升，并行计算越来越成为科学计算的选择.而CUDA (compute unified device architecture) 是由NVIDIA 公司[7]推出的一个通用并行计算架构，该架构使GPU (graphics processing unit) 能够并行地解决复杂的计算问题.由于CUDA 在并行计算方面表现良好，如今的GPU 使用数百个并行处理器内核执行数以万计的并行线程，足以解决具有实质并行性的大型问题.它们是有史以来最普遍的大规模并行处理平台，也是最具有性价比的平台[8].因此，多个学科依托NVIDIA CUDA 平台来实现相关算法的优化[9].

近几年来优化侧信道攻击效率的相关方法主要分为两类: 第一类一般集中于对功耗曲线的处理.例如减少待处理数据的维度，从而降低攻击数据的计算复杂度，进而提高攻击效率等[10-14].第二类则主要考虑提升攻击的计算速度.2010 年，Lee[15]等人提出CPU 与GPU 组合使用的方式可以显著提升侧信道攻击的效果，但未考虑到更大密钥空间的需要，存在一定的局限性;2014 年，Gamaarachchi[16]等人提出将图形处理器(GPU) 应用于CPA 的方法.Gamaarachchi 认为，在通用的CPU 上进行CPA 的时间成本不可观，因此在GPU 上为每一个密钥字节、每一个密钥猜测和每一组功耗曲线分配了一个三维的(目前所能实现的最大维度) CUDA 线程，因此高维的线程实现了更高的数据并行性，但由于显存容量有限，无法处理较多的功耗数据和密钥猜测数量.2016 年，Schellenberg[17]提出了基于GPU 并行加速的一阶和高阶CPA 攻击框架.该框架的可扩展属性可以实现在任意大型服务器集群之间平均分配攻击的工作，从硬件资源角度提高了并行计算的效率.2019 年，王凌云[18]等人提出将CPA 攻击中计算密集的部分都转移至GPU 上实现，带来了较好的攻击效果.但未考虑功耗曲线较多时的传输效率.总的来说，目前相关的研究主要集中于理论上并行程度的提高，大部分未考虑到现实攻击的数据量问题.在现实攻击中由于功耗曲线按行分块存储，读取一个采样点的功耗数据需要多次访存，严重影响攻击的效率.

所以本文针对现实的攻击提出了一种基于并行计算加速CPA 的方法.该方法基于现实功耗曲线分块存储、载入内存时会产生大量时间成本的特点，提出将功耗曲线先转置再并行加速，由此读取曲线一次即可获得该采样点对应的所有功耗数据，再根据CUDA 适用于并行计算的特性，将CPA 部署至GPU，以此获得较高的攻击时间效益.实验数据表明，采用这种方法，可以将一次密钥攻击的范围由一个字节扩增至最大四个字节，能够高效地攻击更大范围的密钥空间.此方法通过数据预处理避免了重复访存所带来的时间成本，同传统的并行计算加速方法相比，密钥空间越大，该方法能够节省的时间越多.

本文第2 节主要介绍CPA 的基本原理，以及利用GPU 的CUDA 编程平台加速CPA 的可行性.同时也介绍计算相关系数时所采用的在线更新算法(Welford’s online algorithm).第3—4 节介绍基于并行计算的侧信道攻击算法的设计与具体实现.第5 节介绍该加速方法的具体实验及优化效果.第6 节总结全文.

2 背景技术

2.1 相关性能量分析(CPA)

相关性能量分析(CPA) 是目前最流行的能量分析手段之一，本文将其作为侧信道攻击的具体实例.攻击时主要有以下步骤:

(1) 采集足够多的功耗曲线并以矩阵形式存储，矩阵每行为每条功耗曲线，每列为采样点;

(2) 选择合适的中间值函数，例如在AES-128 算法中选取位置中间值函数为f(d，k)，d为已知数据，k为猜测子密钥;

(3) 根据中间值函数计算出中间值，假如子密钥有8 位，则对应256 种可能值，即密钥猜测值;

(4) 将计算得出的中间值映射为假设能量功耗值，常见映射模型有汉明重量模型和汉明距离模型等;

(5) 比较假设能量功耗值与实际功耗值，与实际功耗值相关性最高的假设值即为该子密钥的正确密钥猜测值.

在该攻击过程中，攻击者无需了解被攻击设备的详细知识，即使功耗曲线包含噪声难以区分，只要具备足够多的功耗曲线便可成功恢复密钥[3].

2.2 GPU 与CUDA

CUDA[19]是英伟达(NVIDIA) 公司推出的一个通用的并行编程平台.NVIDIA 显卡是支持大量线程并发执行的设备.与现代通用处理器CPU 相比，两者结构类似，都具有用于计算的核，但CPU 内核较少，内核集中用于快速处理单个任务，因此CPU 适合处理复杂的串行计算.GPU 核数较多，适合较简单的并行工作.CPA 数据独立性较高，GPU 的并行特点可以极大地提高其攻击性能.Block 和Grid 是CUDA 编程上的概念，Grid、Block 和Thread 都是线程的组织形式，Thread 是最小的逻辑单位，一定数量的Thread 组成一个Block，一定数量的Block 组成一个Grid，核函数在执行时应配置合适的Grid 和Block 大小.

Numba[20]开源软件包的提出使我们可以使用Python 编程语言[21]对CUDA 进行编程，并且Numba 提供了一系列函数实现了分配设备内存、在主机与设备间拷贝数据等功能.另外CUDA 支持高达三维的线程索引，多维线程层次结构使我们能够方便地将并行化算法的组件映射到GPU 线程上.例如，一维线程索引映射为向量操作，而二维线程索引映射为矩阵操作.在使用时，核函数会根据需要被分配给N个不同的线程(Thread)，N个线程并行执行，以达到并行计算加速的作用.对于一个特定的CUDA内核，线程块的大小是相等的.用户必须在调用CUDA 内核时指定线程块大小，一个线程块最多设置1024 个线程.线程块的大小是影响CUDA 并行性能的一个重要因素，需要谨慎选择合适的参数.

2.3 在线更新算法

在CPA 中，皮尔逊相关系数计算需要计算方差，但是经典方差公式涉及平方和，这极容易出现数值不稳定或算术溢出等问题.在线更新算法[22]使用逐次更新的加法计算方差，因此解决了前文提出的安全隐患.同时在处理侧信道数据时可以做到每读取一条曲线，对结果进行一次更新.计算相关系数需要预先计算协方差和方差，因此使用以下公式进行计算:

2.4 常用的侧信道攻击并行模式

常用的侧信道攻击并行模式: 目前常见的基于CUDA 并行计算加速CPA 的基本方法是将攻击过程中的几个要素并行化.例如将密钥猜测数量、采样点、密钥位数等映射为CUDA 核函数对应的维度，以此来实现合适的并行计算[16，18].

此处以AES-128[23]第一轮S-box 之后的泄漏为例，一个完整的二维GPU 加速CPA 攻击设计流程如下:

(1) 获取中间值矩阵D.将密码设备每次执行的数据值di通过穷举密钥猜测得到假设中间值矩阵D，再通过能量映射模型对中间值进行能量映射，本文采用汉明重量能量映射模型，最终得到假设能量消耗矩阵D和对齐的功耗曲线T.

(2) 设计核函数.其中图1 展示了CPA 攻击二维核函数结果矩阵的组织，图1 中网格代表了一次密钥猜测的相关性结果矩阵R，灰色格子代表了一个二维线程执行核函数的结果，即针对相关性结果矩阵R每个点对应的核函数分配二维的线程，所以灰色格子是密钥猜测以及功耗曲线泄漏位置的组合.攻击时，在GPU 中将每一个计算相关性系数的过程并行化，分配二维CUDA 线程，建立计算相关性的核函数.该核函数的功能是计算假设能量值矩阵每一列(d1，k，d2，k，···，dD，k)与功耗曲线的每一列(t1，j，t2，j，···，tD，j) 的相关系数，并存储到相关性矩阵R.其中与计算的结果为Rk，j.

图1 二维CUDA 核函数Figure 1 2-D kernel example

(3) 二维核函数的实施.该核函数的功能是计算假设能量功耗值D每列数据(即每种密钥猜测) 同功耗曲线T每列数据(即每个采样点) 的相关性系数.根据功耗曲线按行存储、按行读取的原则，相关性系数计算公式一般使用此公式:

(4) 直至所有假设能量功耗值数据和功耗曲线全部载入内存，即可根据最终的每列的方差和协方差计算相关系数.在这个过程中，每组数据之间的相关性系数互相独立可以并行计算.

(5) 将相关性系数矩阵为Rk，j拷贝至CPU.对相关性系数矩阵为Rk，j进行处理获取最大值及其对应的横纵索引，这个阶段需要并行的任务数量较少，调用CUDA 内核成本较高，因此本文选择在CPU 端进行该阶段的处理.由此，即可获得相关性系数的最大值对应的密钥猜测以及功耗曲线中的泄漏位置.

2.5 需要解决的问题

并行计算应用于侧信道攻击，给该领域带来了显著的计算性能提升，但并行计算通常需要同时调度多个计算单元.目前，计算机硬件的性能参数有上限，难以负载较大规模的功耗曲线.大多数情况下，使用将收集曲线存储在外部存储器中的方法来缓解硬件设备的不足，但这种方法增加了现实攻击的难度.因为数据的分块存储会导致读取传输时间的增加.特别是CPA 需要特定采样点的全部功耗数据，功耗曲线按照曲线条数进行存储，这意味着在进行CPA 攻击时，需要多次访问外部存储，以获得与特定采样点对应的所有功耗数据.这将产生相当大的时间成本.

所以要解决的问题为:

(1) 尽可能降低攻击数据在外部存储器与内存之间频繁传输带来的时间成本;

(2) 在有限的硬件资源条件下合理权衡并行计算性能与攻击所用数据规模的问题;

(3) 进一步扩大一次攻击密钥的范围，提高实际应用中密钥攻击的灵活度.

3 新的并行方法

因此本文提出另外一种并行方式.这种并行方式首先对功耗曲线进行快速转置预处理，具体为将每个采样点数据从分块存储的一列转化为集中存储的一行，实施正式攻击时只需访问一次存储设备便可获得该采样点的所有功耗数据.然后将穷举不同密钥猜测的过程并行化，一次攻击一个采样点.

3.1 总体流程

总的来说，如图2 所示，本文的并行方法主要分为两个阶段.

图2 攻击总体流程图Figure 2 Attacking overall flow of DPA

第一阶段: 对大规模分块存储的功耗曲线进行转置.该步骤可以得到按行存储的逐个采样点数据.这个阶段的难点是如何对大规模分块存储矩阵进行快速转置，这也是该部分介绍的重点.

第二阶段: 在并行计算模型上部署CPA.由于第一阶段得到了按行存储的逐个采样点数据，因此针对某个采样点进行攻击时，只需读取外部存储器一次便可得到所需全部数据，然后选择合适的并行策略，设计核心攻击函数，针对多个密钥猜测同时进行攻击.这个阶段将在第4 节详细介绍.

3.2 功耗曲线预处理

功耗曲线的预处理阶段目标是在现实攻击时，读取文件一次，便可获得某个采样点的全部功耗数据，同时这个转置操作应尽可能降低时间复杂度，减少访问外部存储器的开销.如算法1 和图3 所示，Ai为功耗曲线分块矩阵;功耗曲线块数为N;每块矩阵重新分组数为M;Ai转置过程中的中间矩阵为Ci;Bj为最终转置完成的功耗曲线.

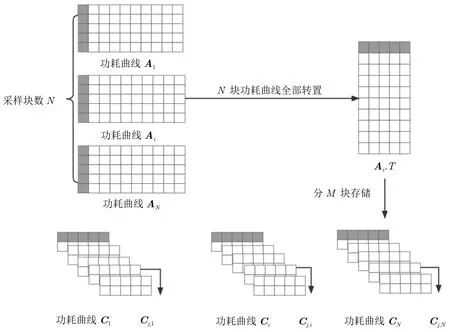
图3 矩阵转置后分块存储Figure 3 Transposition and storage of a matrix

3.2.1 矩阵转置后存储至外部存储器

在这个阶段，本文主要对分块存储的功耗曲线进行以下操作:

(1) 将每块功耗曲线读取至内存进行转置操作.由于每块功耗曲线的大小是根据硬件资源来进行设置，因此在该硬件资源环境下可以直接进行矩阵的转置操作.本文使用NumPy[24]提供的开源转置算法，其转置效率较高.Ai转置后矩阵为Ci.

(2) 将转置后功耗曲线进行分块存储.这个阶段首先根据被攻击设备的硬件内存计算出攻击时所能提供的运行内存上限MAX(Memory)，攻击时一块数据的大小命名为SIZEOF(Bj).再根据数据块的数量N，以Bj/M×N ＜MAX(Memory) 原则(即不超过硬件资源上限)，设置合适大小的每块重新分组数M.

(3) 重新分块后每块数据成为Cj，i，i对应原始数据Ai的块顺序i，j对应转置后数据Ci内部分块存储的块顺序j，即Cj，i代表第i块原始分块存储功耗曲线转置后分块存储的第j块.

3.2.2 重新组织为新矩阵

上一阶段获得了重新分块的数据Cj，i.接下来在硬件内存允许条件下，根据Bj/M×N ＜MAX(Memory) 的原则，如图4 所示，将i值不同j值相同的数据块按列顺序拼接，即将同一采样点的数据拼接，即可得转置后的包含原始功耗曲线整列的转置矩阵.处理完毕后，相关系数矩阵中的每一行数据对应原始功耗曲线中某个采样点所采集出的功耗数据.算法1 展示了功耗曲线预处理转置的全部流程.

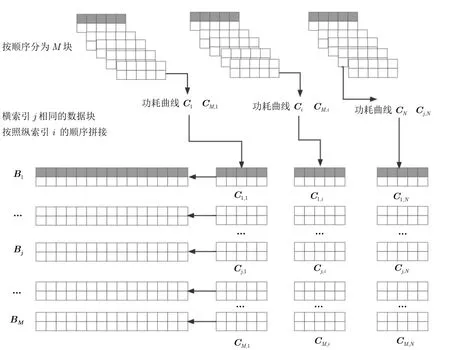
图4 Cj，i 拼接Figure 4 Combination of Cj，i

3.3 预处理转置算法性能分析

对于现实CPA 来说，攻击所需的功耗曲线是大量的、分块存储的矩阵.我们无法避免分块读入功耗曲线导致的频繁访存，但采取上文方法只需遍历所有功耗曲线两次便可实现整个数据文件的完全转置，这极大地提高了矩阵转置的效率，进一步保障了后续CPA 的攻击性能.

4 GPU 平台上的并行算法

4.1 CUDA 核函数实现

本文给出的核函数实现如算法2 所示，具体如下: 同时启动多个线程，每个线程处理一种密钥猜测.众所周知，数据传输一直是GPU 并行计算的瓶颈所在.为减少数据传输所用时间成本，本文将计算中间值矩阵的过程转移至GPU.因此，需要从CPU 传输给GPU 的只有两种数据: 明文以及转置后的功耗曲线.由于一次只传输一个采样点的全部数据，这种情况下，可以不考虑曲线的分块存储，所有需要的数据可以一次从CPU 拷贝至GPU.

如图5 所示，这里p描述了一组明文，其中i是明文序号.在该图中，明文的数量为n，因此对应的功耗曲线数量同样为n;k代表了一次攻击的密钥，j代表了不同的密钥猜测，图中一次攻击m个密钥猜测.每个明文与所有的密钥猜测通过中间值计算函数(具体的加密或解密算法以及功耗能量映射模型) 计算出中间值value，由此得到中间值矩阵.每个密钥猜测被分配给一个线程.例如线程1 被分配给密钥猜测为k1对应的中间值矩阵的一列，而线程2 被分配给密钥猜测为k2对应的中间值矩阵的一列，以此类推.

图5 CUDA 核函数设计Figure 5 Design of CUDA kernal

CUDA 内核函数规定了一个线程应该执行的所有工作: 该线程读取参与攻击的拷贝至GPU 的明文，计算出明文针对具体算法的汉明重量映射的假设能量功耗值，再将其同实际功耗曲线进行相关性系数的计算.因此当多个线程并行启动时，每个线程计算一种密钥猜测，所有线程都会调用相关性计算函数并计算出功耗数据与假设能量功耗值的相似度.最后调用原子函数获取相关性系数的最大值.

在配置CUDA 核函数时，Block 的设置应该遵循SM 占用率最大化原则，Warp 是SM 的基本执行单元.一个Warp 包含32 个并行Thread.即使最后一个Warp 中有效的线程数量不足32，也要使用相同的硬件资源，所以Block 的大小最好是32 的倍数.Warp 与Block 的关系为:

根据多次实验验证，Block 的大小取128 效果最优.

4.2 总体流程

总的来说，如图6 所示.

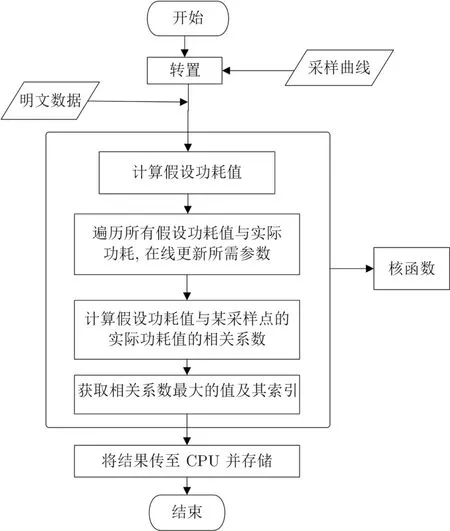
图6 使用GPU 平台部署攻击总体流程图Figure 6 Attack overall flow using GPU

(1) 实现矩阵快速转置: 该过程需遍历全部功耗曲线两轮.处理完毕后，相关系数矩阵中的每一行数据对应原始功耗曲线中某个采样点所采集出的功耗数据.

(2) 攻击: 对应数据矩阵，为减少数据从外部存储器拷贝到显卡内存的时间成本，将假设能量功耗值矩阵的计算转移至GPU 中，为每一个密钥猜测分配一个Thread.以AES-128 为例.核函数的组织如下: 根据明文和密钥猜测计算出AES-128 第一轮MixColumn 或S-box 之后的中间值，并将汉明重量作为能量映射模型，最终得到假设功耗值矩阵.若密钥猜测的比特数为N，则有2N种密钥猜测，每种密钥猜测对应一列假设能量功耗值.故对一组明文来说，有2N列中间值.因此分配2N个线程.

(3) 从外部存储器读取处理后的功耗曲线矩阵，将一行数据从CPU 拷贝至GPU，在GPU 上关于每种密钥猜测同该行数据计算相关系数.并将结果暂时存储在GPU 中.

(4) 运行核函数，得到关于所有密钥猜测假设能量功耗值与采样功耗值的2N个相关系数之后，通过调用原子函数atomic.max，在2N个相关性系数中取最大值max_value，并记录下对应的索引下标max_index，索引下标即为密钥猜测，最后将GPU 计算结果传至CPU 即可得到关于某采样点相关性最大的密钥猜测.

(5) 通过对功耗曲线的转置，本文的方法成功避免了功耗曲线分块读取带来的时间损耗.这种情况下，密钥猜测位数的范围极大地延伸，以AES 为例，以往攻击位置一般选择第一轮的S-box 之后或最后一轮S-box 之后，而密钥并行方式则可以将攻击位置向后推至MixColumn 之后，一次可攻击更多的密钥.这在CPU 上是计算上不可行的.

5 实验

5.1 实验设置

本文中实验使用了Python 3.8、CUDA 11.2 以及Numba 0.44 环境，搭载了Intel(R) Xeon(R) Gold 6330 CPU 处理器，NVIDIA RTX A5000 显卡、NVIDIA RTX 3090 显卡以及NVIDIA GTX 1050Ti显卡，其中三种显卡的算力为: 8.6、8.6、6.1.使用了AES_HD 公共数据集，该数据集分块存储，每块有25 000 条功耗曲线，每条功耗曲线有1250 个采样点.需要注意的是，由于实验目标是验证本文的并行加速方法能够带来比CPU 和以往的并行计算方式更好的效果，因此比较的指标是对相同数据进行攻击操作时消耗的时间.另外，为了尽可能攻击更多位数的密钥，本文一次只攻击一个采样点的数据.

5.2 CPU/GPU 计算时间开销对比

该实验选取了25 000 条功耗曲线.图7 显示同一数据集在CPU 和不同GPU 平台上的执行时间随密钥猜测位数的变化而变化，并且密钥位数相同的情况下CPU/GPU 计算时间成本差异较大.当密钥猜测位数在6—14 位之间时，CPU 上的执行时间几乎随密钥猜测位数的增长呈指数增长.而GPU 上的时间成本从图7 看似乎始终接近于0，这是因为与单线程的CPU 计算相比，并行计算的GPU 时间远远低于单线程CPU 的运算时间.

图7 不同密钥位数情况下CPU/GPU 计算时间对比Figure 7 Running time comparison on different key lengths

因此把两种GPU 单独拿出来放大展示.图8 为A5000 以及GTX 1050Ti 的时间成本对比.在起步阶段使用GPU 进行攻击运算不会提高性能.原因是密钥猜测位数较少的情况下并行运行启动的线程也比较少，这不足以隐藏GPU 中的内存延迟.因此当密钥猜测数量很少时，GPU 架构可能会比CPU 消耗更多的时间.但总的来说，随着密钥猜测位数的增长，并行计算可以带来较好的加速效果.

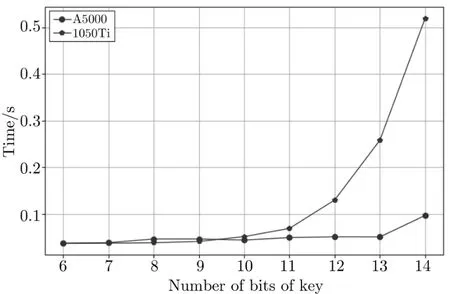
图8 6-14 位密钥猜测GPU 计算时间对比Figure 8 GPU running time comparison regarding 6–14 bits of guessing key

5.3 不同GPU 并行效果

A5000 有8192 个CUDA 核，3090 有10 496 个CUDA 核，而1050Ti 有768 个CUDA 核.因此在计算量较大、需要的并行线程数量较多时，理论上3090 显卡应优于A5000，A5000 应优于1050Ti.本实验使用25 000 条功耗曲线.

如图9 所示，当密钥猜测位数低于20 时，三种GPU 效果基本相同.这是因为，如果密钥猜测位数少，并行运行的线程启动的也比较少，这不足以在GPU 中隐藏内存延迟.如果密钥猜测位数超过20，GPU的执行时间将随着密钥猜测位数的增加而以指数方式增加近一倍.在这样的并行度下，内存延迟是隐藏的.但是，随着密钥猜测位数的增加，如果密钥猜测位数大于22，则在加速相同大小的数据集时，3090 GPU 的时间将明显少于A5000 和1050 Ti.

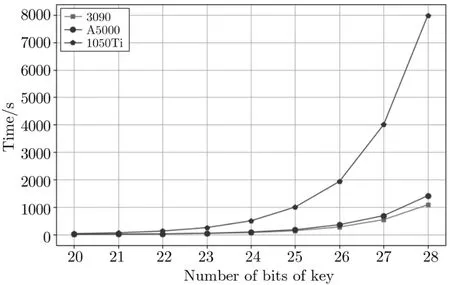
图9 三种GPU 时间对比Figure 9 Running time comparison on different GPUs

因此，如图10 所示，当攻击32 bit 密钥时，选择使用Nvidia RTX 3090 显卡，最终所用时间为17 646.4 s，约4.9 h.

图10 Nvidia RTX 3090 性能Figure 10 Nvidia RTX 3090’s performance

5.4 不同加速方式对比

5.4.1 不同加速方式详细对比首先对并行加速侧信道分析工作做分析对比，如表1 所示.由于Schellenberg[17]文中一阶CPA 的加速实现与Lee 等[15]基本一致，故表中仅列出Lee 的方法.

表1 不同并行加速方式对比Table 1 Comparison of different parallel method

5.4.2 不同并行加速方式性能对比

实验选取5000 条功耗曲线.使用NVIDIA RTX A5000 显卡，显卡内存为24 G.如图11 所示，该图体现了处理相同数据集时，随着攻击密钥猜测数量的增加，不同计算方式性能的变化.

图11 不同计算方法与本文方法对比Figure 11 Comparison of different algorithms

从图中得出，经典CPA[5]由于未考虑并行加速计算密集部分，加速效果始终低于其他加速方法;Lee[15]的方法使用CPU 与GPU 组合使用的方式相比于经典CPA 方法可以显著提升侧信道攻击的效果，但未考虑到更大密钥空间的需要，因此随着密钥空间的增大，其优化效果有限;而Gamaarachchi等[16]的方法由于建立了较高维度的计算模型可以实现较高的并行度，但这种高度并行策略会占用较多的硬件资源，不适用于密钥空间较大的情况.

当密钥猜测位数较少时，王凌云等人[18]的并行计算方法性能优于本文方法，这是因为密钥猜测位数较少的情况下并行运行的线程启动的也比较少，这不足以隐藏GPU 中内存延迟;但随着密钥猜测位数的增加，需要传输的数据越来越多，显卡的硬件资源面临的压力逐渐达到上限，必须通过减小数据规模、增多数据分块数的方式来以时间换空间，最终达到硬件上限，止步于密钥猜测位数27，此时本文方法计算时间仅为王凌云等人[18]并行方法的3.67%.而本文方法从密钥猜测位数为13 位时开始逐渐显出优势，最高密钥猜测位数可达32 位.随着密钥猜测位数的增加，本文方法的时间成本始终平稳增长.

6 总结

本文提出了一种基于并行计算的侧信道攻击加速方法.该方法首先提出了一种功耗曲线快速转置的策略，这种策略在密钥猜测数量极大时读取一次外部存储器即可获取整个采样点的功耗数据.基于这种快速转置策略将所有密钥猜测并行化，可以实现同时对更多密钥猜测的攻击.此方法通过数据预处理避免了重复访存所带来的时间损耗，因此当密钥空间越大，该方法能够节省的时间越多.并且，这种加速方法可以将被攻击密码算法的攻击位置向后推动，进一步扩大CPA 攻击算法的范围.另外，本方法只是对并行计算加速侧信道攻击的初步探索，下一步可以优化并行计算方案.例如优化并行计算模块内部的数据存取以及并行计算各模块之间的数据传输，进一步减少数据传输带来的时间成本，用以进一步探索并行计算平台对侧信道攻击领域带来的有益效果.值得一提的是，相关能量分析是功耗分析的基础，本文介绍的方法也适用于加速很多其他的功耗分析方法(如基于模板的差分功耗分析[25]、互信息分析[26]、通用侧信道分析[27，28] 等).