极限梯度提升声品质预测模型在车内噪声主动控制中的运用

欧 健，彭沸潭，张庆庭，覃 亮，杨鄂川

（1.重庆理工大学车辆工程学院，重庆 400054；2.重庆大江智防特种装备有限公司，重庆 401320）

引言

噪声不仅对人的生理，而且更重要的是对人的心理，尤其是对神经系统的影响更为严重［1］。在恶劣的噪声环境下，驾乘人员会出现精神紧张、心情烦躁、注意力分散等情况。长时间的噪声污染更是加大了心脑血管疾病的患病可能［2-3］。特种车辆的使用环境往往比乘用车或商用车更为恶劣，道路条件更加不理想，甚至是在没有道路的地形上使用，这样的条件下遇到的噪声振动激励种类变多，驾驶室内的噪声问题更加严重。由于特种车辆的用途特殊性，许多政府以及企业也开始严格要求控制特种车辆的噪声和振动方面的问题。因此针对特种车辆车内噪声的研究具有十分迫切的需求和重要的意义。

传统的噪声研究更多地关注声音信号本身的一些传统物理参数，但人是噪声的最后接收者，在研究声音本身时，也同样需要考虑人的主观感受。因此，许多专家学者提出了声品质的概念，旨在用更丰富的维度去描述声音的性质以及人的主观对声音的评价。

考虑到主观评价的耗时耗力，越来越多的学者开始找寻新的突破口，目前为止，已经有很多关于声品质主/客观量化模型和声品质预测的研究。高印寒等［4］提出了用GA-BP神经网络预测B级车车内噪声品质，实验表明该神经网络模型的输出结果与实际的主观评价分数之间的相关系数可达0.928，随后还分析了选取的7 个客观参数对结果的贡献度。夏小均等［5］提出了基于支持向量机的方法，利用因子分析、相关分析和聚类分析完成了车内稳态噪声样本的降维，提取了贡献量较大的参量，最后验证了模型的预测能力和精度，也证明了降维处理方法的有效性。

Oliveira 等［6］、Li 等［7］分别采用FxLMS 算法进行主动降噪，结果表明都取得了不错的降噪效果。汽车行驶过程中，车内噪声来源众多，信号具有非线性、非平稳性的特点。小波分解和EMD分解都可以用来降低噪声信号的非平稳度［8-9］，但小波分解在处理信号前需要提前确定小波基和分解尺度，受主观影响较大。而EMD 分解根据信号自身特点，具有良好的适应性［10］。

目前声品质评价领域主要采用BP 神经网络，但其梯度下降算法存在初始连接随机性强、收敛速度慢等缺点。同时神经网络还局限于客观参数对主观评价的影响［4］。本文以某特种车为主要研究对象，计算特种车车内噪声的客观参数，并对噪声进行了主观评价，利用机器学习方法XGBoost 建立声品质预测模型并验证模型的有效性，同时针对声品质客观参数的特点计算分析客观参数对主观分数的影响权重。针对车内噪声信号呈现非线性、非平稳性的特点，通过经验模态分解噪声：1.验证了影响主观评价分数的主要因素能得到有效控制；2.以验证影响主观评价分数的主要因素能否得到有效控制。

1 理论分析

1.1 XGBoost 声品质预测模型

XGBoost 是Chen 等［11］提出的一种基于提升树的机器学习系统。在有限次数的迭代过程中形成最终的接近实际值的模型。通过迭代残差树的集合，具有良好的防过拟合特性［12］。

XGBoost 训练模型就是要获取最优的损失函数Θ，使输入值xi和输出值yi的回归效果可以达到最优。模型支持交叉验证，以及可以在设定的迭代次数之前停止树的生长，从而避免无效计算拉低效率。同时还支持并行训练，训练时间短，在各个层面提高了模型的准确率以及预测精度。

在训练模型中定义一个目标函数，其中包括训练误差和正则项，用来表征模型与训练集的匹配程度和模型的复杂度：

式中K表示树的数量；F表示特征空间；f表示特征；yi为样本的真实值为样本的估计值；L(θ)为样本的均方根误差之和；Ω(θ)为正则项。

假设在第t步预测的值为，则有：

将式（7）代入到训练误差函数L(θ) 中，并对误差函数进行泰勒展开，目标函数改写为：

正则项Ω(f)中又包含两个部分：

式中T表示叶子结点的个数；ωj表示叶子权重；γ表示叶子总量对目标函数施加的惩罚系数；λ表示叶子权重的大小对目标函数施加的惩罚系数。

将正则项代入式（9）得：

式中ωq为叶子节点分数。

1.2 XGBoost 权重分析

在XGBoost 预测模型中通过对给定的数据集中的特征点进行分割，从而使整个预测树模型的平均增益最大，这意味着这个特征被分割的次数越多，这个特征越重要。在分割过程中，每个分割点的权重可以表示为w(gi，hi)，其中gi和hi分别为：

根据特征点的权值，考虑其增益Gain，则有：

式（13）说明其分割点增益等于分割后权重（左、右子树总权重之和）减去分割前权重。

1.3 主动降噪算法

研究表明，传统的汽车噪声控制方法，主要采用吸声材料以及机械结构的优化设计等措施达到降噪的目的，对波长短的高频噪声有较好的降噪效果，而且都需要特定的材料和机械结构，对工艺及成本的要求较高。目前，车内低频噪声仍未得到良好控制。近年来，声品质主动控制因其具有主动性、选择性、频率适用范围广、降噪性能可靠等优点逐渐被运用到车内噪声的控制中［13-15］。

FxLMS 算法目前已经成为有源控制算法的基准算法，因其具有实现简单、运算量小且稳定性强的特点，在车内噪声控制中被广泛运用。

FxLMS 算法框图如图1 所示。x（k）为噪声源信号；P（Z）为初级传递路径，指噪声源传递到误差传感器的路径；d（k）为期望信号；W（Z）为滤波控制器；y（k）为抵消噪声信号；S（Z）表示次级传递路径，为扬声器发出的次级声源传递到误差传感器的路径；S'（Z）是对次级传递路径S（Z）的无偏估计，理论上两者相等；F（k）为控制器的输入信号；s（k）表示抵消噪声；e（k）为误差信号。

图1 FxLMS 算法框图Fig.1 FxLMS algorithm block diagram

FxLMS 算法以误差信号e（k）最小均方为原则，通过最速下降法进行迭代。控制器输出信号y（k）为：

式中wT（k）为滤波器的系数向量的转置。

y（k）传到误差传感器处有：

式中s（n）是S（Z）的脉冲响应。

误差信号e（k）可表示为：

滤波信号F（k）为：

式中是S'（Z）的脉冲响应。

更新滤波器W（Z）的系数：

式中u为步长因子，其选择会影响算法的收敛速度和最小均方误差，收敛范围为：

式中λmax为滤波信号F（k）自相关矩阵的最大特征值。

通过对原始信号进行 EMD 分解，原始信号X（t）可表示为：

式中X（t）为原始信号；IMFi（t）为各固有模式函数分量；m为IMF分量数；r（t）为残差。

FxLMS 算法再对经过EMD 分解后的每一个分量进行控制。EMD-FxLMS 算法框图如图2 所示，其中Cj(k)为最大固有模式函数分量。

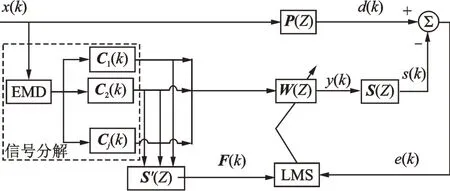
图2 EMD-FxLMS 算法框图Fig.2 EMD-FxLMS algorithm block diagram

2 车内噪声样本采集与处理

车内噪声采集试验条件参考相应国家标准［16-17］，主要试验设备有：待测车辆、LMS 数据采集前端、LMS Test.Lab 的测试系统、传声器及BNC 线缆若干等。特种车内测点位置包括：主驾驶右耳处、副驾驶左耳处、后排乘客处。

为了增加后续预测模型的准确性，防止过拟合，需拉大样本的差距，故在此加入样车2 匀速工况，实验最后得到68 个有效声音样本。测试工况与测点位置如表1 所示。

表1 测试工况与测点位置Tab.1 Test conditions and measuring point locations

将评分系统设置为10 个等级，分值从1 到10 分别对应主观感受的满意程度，如表2 所示。

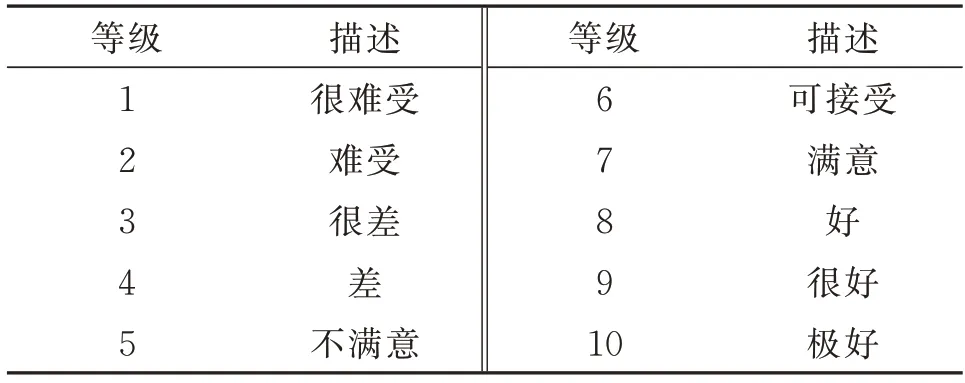
表2 烦躁度等级对照Tab.2 Comparison of irritability rating

选取25 名评价人员进行主观评价，评价人员身体健康且听力正常，其中男生20 名，女生5 名，均持有驾照，且有一定的驾驶经验和丰富的乘车经验。表3 为部分评价分数。

表3 部分评价分数Tab.3 Partial evaluation scores

主观评价结果的有效性采用Pearson 相关系数r进行判定。其计算公式为：

式中s为样本数量；xi为主观评价分数；yi为客观评价参数；“-”表示平均数。

计算各个评价人员与主观评价分数的算术平均值的Pearson 相关系数，最后得到如表4 所示的各评价人员的相关系数。

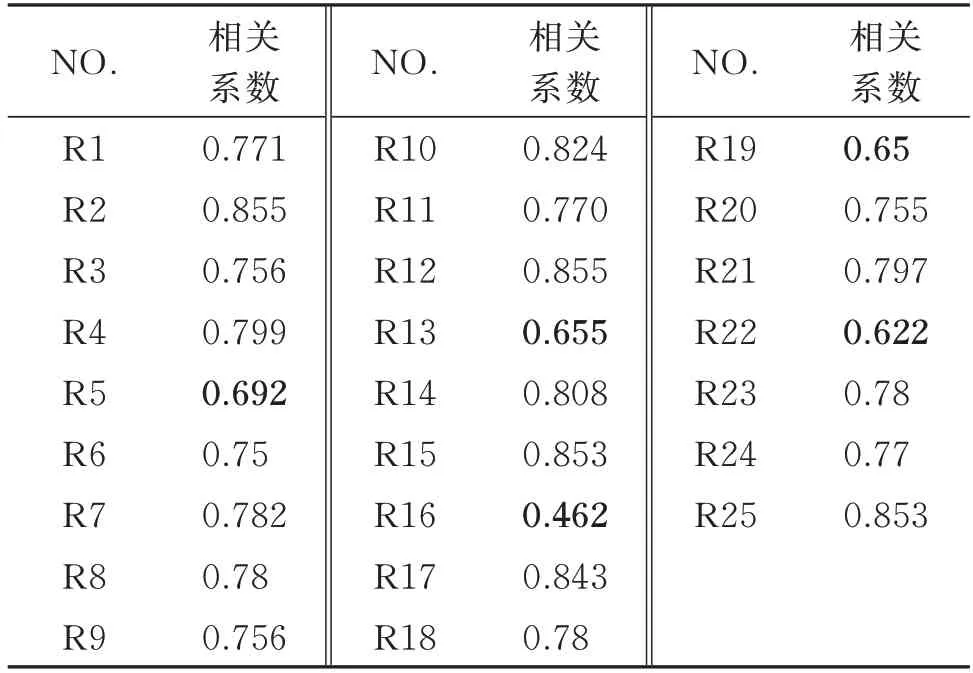
表4 各评价人员的相关系数Tab.4 Correlation coefficients of each evaluator

在统计学中，相关系数小于0.7 时视为变量之间相关性较差，因此删除编号为R5，R13，R16，R19，R22 的5 名评价人员的评价结果。

根据响度、尖锐度、粗糙度、以及AI 指数的计算公式，完成计算后对这些参数进行记录统计。表5所示为68 个声音样本部分客观参数以及主观评价分数。

表5 部分声音样本的主/客观评价结果Tab.5 Subjective and objective evaluation results of some sound samples

3 实验验证

3.1 XGBoost 模型训练与检验

从声音样本中抽取20%作为测试集，然后验证测试集中随机10 个样本的预测值与真实值之间的相对误差，结果如图3 所示。

图3 真实值与预测值的相对误差Fig.3 The relative error between the actual value and the predicted value

将测试样本真实值与预测值进行对比，结果如图4 所示。

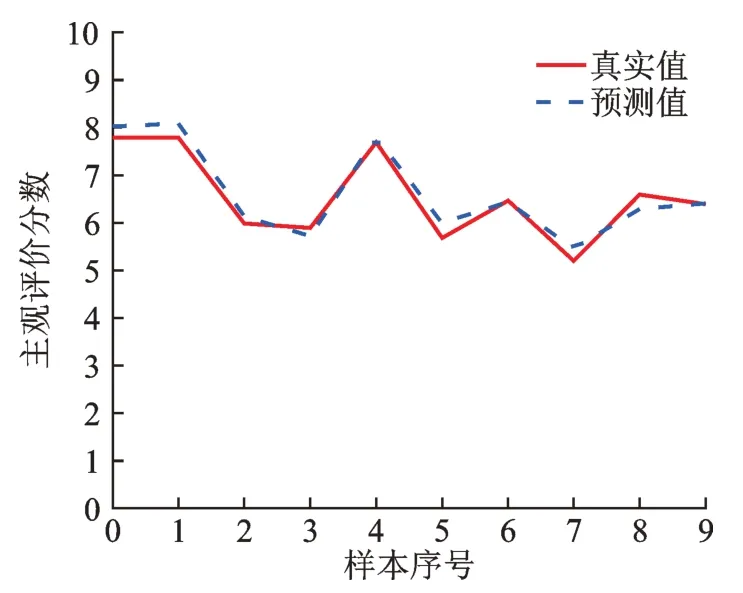
图4 预测结果对比Fig.4 Comparison of predicted results

XGBoost 预测模型的平均相对误差为2.43%，相关性系数为0.943。为了验证XGBoost 预测模型的精度，通过对比GA-BP 神经网络与随机森林模型的平均相对误差（MRE）和相关性系数（R2），如表6所示。结果表明，XGBoost 预测模型能更好地实现客观参数预测主观评价。

对声品质而言重要性分数就是客观参数对主观评价的影响程度。重要性分数越高，则影响程度越大；重要性分数越低，则影响程度越小。各参数的重要性分数如图5 所示。

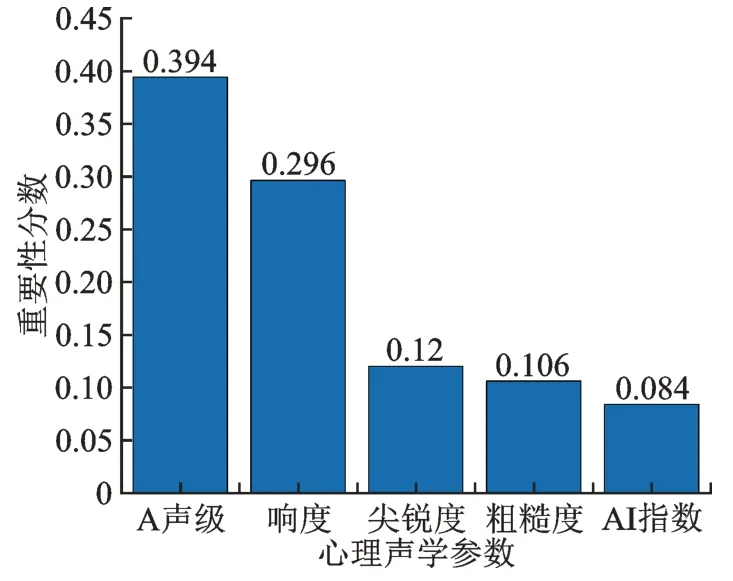
图5 各参数的重要性分数Fig.5 The importance scores of each parameter

由图5 可知，在选取的5 种客观参数中，A 声级、响度对预测主观评价分数的贡献度较大。这表明在对稳态工况下的特种车车内声品质进行评价分析和优化时，只需要考虑A 声级和响度，不需要考虑其他过多参数的影响就能得到比较满意的结果，减少了测试分析时间，提高了工作效率。

3.2 声品质主动控制

选取采集噪声中主观分数较低，且特种车以较低速度30 km/h 行驶，主驾驶右耳处的噪声进行分析。

对噪声信号进行EMD 分解，共得到10 个IMF分量，结果如图6 所示。

图6 EMD 分解波形图Fig.6 EMD decomposition waveform diagram

在MATLAB 环境下，根据本文建立的控制算法编写程序，然后分别以两种算法对噪声进行主动控制，控制结果如图7 所示。

图7 EMD-FxLMS 与FxLMS 算法控制结果对比Fig.7 Comparison of control results between EMD-FxLMS and FxLMS algorithms

从图7中可以看出，经过两种算法主动控制后，残余噪声波形均收敛为细窄的条状，但EMD-FxLMS的幅值更小，收敛速度更快。在11.5 s 时车内噪声出现较大波动，EMD-FxLMS 能更好地控制残余噪声的幅值。

表7 显示了控制前后声品质客观参数的变化。从表7 中可以看出，A 声级、响度与AI 指数有明显的优化，而尖锐度与声音中高频成分占比有关，一般高频占比越大，声音的尖锐度越大。主动控制一般针对噪声中低频成分，导致控制后尖锐度有所增加。

表7 控制前后声品质客观参数Tab.7 Objective parameters of sound quality before and after control

由主观评价的权重分析可以看出，降低A 声级、响度能有效提高主观评价分数。

为进一步验证控制后声品质的改善情况，将控制后的噪声导入XGBoost 预测模型，同时对噪声进行主观评价，结果如图8 所示。通过EMD-FxLMS算法控制后，主观分数由5.81 提升到7.92，提升幅度为26.6%，能有效改善车内声品质。

图8 控制前后烦躁度等级Fig.8 The irritability rating before and after control

4 结论

以某特种车车内声品质为研究对象，进行了车内噪声的采集试验并整理声音样本，利用极限梯度提升算法建立客观参数与主观评价的预测模型，其平均相对误差为2.43%，相关性系数为0.943。同时针对声品质客观参数的特点分析得到客观参数A声级、响度对预测主观分数的贡献度较大。

在残余噪声的收敛性与收敛速度上，EMDFxLMS 算法都优于FxLMS 算法；在声品质控制上，主观分数提升2.11，提升幅度为26.6%，能有效改善车内声品质。