改进小波阈值函数在手部姿态获取中的应用*

徐晗昕，俞斌杰，柳 丽，3，王 英，3，杜森浩

（1.宁波大学机械工程与力学学院，浙江 宁波 315211；2.浙江智马达智能科技有限公司，浙江 宁波 315336；3.浙江省零件轧制成型技术研究重点实验室，浙江 宁波 315211）

0 引 言

手在人们日常生活中起着重要的作用，手功能障碍患者及时进行有效的康复训练对加快恢复有着十分重要的影响［1］。然而康复训练周期长，多次往返医院的经济、时间成本高，因此，迫切需要对手部康复训练装置及系统进行设计与开发，让手部康复训练智能化、便捷化。

手部康复系统中，手部姿态获取方式主要有机器视觉和数据手套等。杨文璐等人［2］、Lapiana N 等人［3］、Xue Y等人［4］利用机器视觉于康复系统中，但该方式容易受到光线、遮挡等因素影响，且要求使用系统的患者手部须一直放置在摄像头能够拍摄到的范围内。龚文等人［5］、赵裕沛等人［6］、Wang D等人［7］设计了力反馈数据手套，利用传感器采集手部运动姿态信息，具有普适性。然而，由于微加工技术与集成工艺技术的限制和使用过程中外界环境多变等因素，使得传感器输出信号检测不准确。如何高效降噪，提高传感器输出信号的精度这一难题亟待解决。

广受青睐的小波变换法由于独特的多分辨率特性能够更好地分解非平稳信号，有效滤除噪声干扰［8］。小波变换常用的方法包括模数最大法、系数相关法和阈值降噪法，其中，小波阈值法降噪具有计算速度快、信号保留完整等特点，得到了广泛应用。

由Donoho教授于1995年提出的著名硬、软阈值函数，其优点主要表现为易于实现，运算简单，且变换后能够降低熵值，但实践应用中该方法仍然存在不足和缺陷［9］。硬阈值函数能较好地保留信号的局部边缘特征，但在阈值处不连续，会导致小波重构时出现较为明显的振荡。软阈值函数弥补了硬阈值函数在阈值处不连续问题，但其处理的小波估计系数与信号的小波系数之间存在固定偏差，使得部分信号丢失，影响了小波重构后原始信号的还原度。为此，研究人员采取了很多方法进行阈值函数的改进。Fong J等人［10］提出一种利用粒子群优化算法调整参数的改进小波阈值函数，并结合贝叶斯收缩阈值法重构小波系数；孙然然［11］提出CALE 阈值函数，通过在不同的分解层数设置不同的阈值使得阈值处具有连贯性；赵薇等人［12］提出一种双参数阈值函数，通过加入调节参数使得改进的阈值函数能在硬阈值与软阈值函数之间切换；甘若等人［13］提出将阈值函数与对数函数相结合解决传统阈值函数不连续、失真等问题；田江龙等人［14］基于改进硬阈值法和双变量小波阈值函数的方法使去噪后的信号在过分平滑与边缘振荡现象之间达到合理的平衡。以上改进策略中，或引入了多个暂定参数加大了计算量，或函数过于复杂加大了计算难度，降低了传感器数据输出的实时性。李朋等人［15］提出将阈值函数阈值内部分的小波系数从置零改为一定数值解决在阈值处间断的问题，但仍不可避免会保留一部分噪声。

针对手部康复系统对真实手与虚拟手运动同步性及精准性要求，本文基于极限的思想提出一种改进小波阈值函数，在不额外添加调节参数的前提下，解决传统阈值函数不连续、失真等问题，使去噪信号无限逼近与原始信号，同时保证传感器数据传输的稳定性、实时性。

1 小波阈值去噪原理

首先采用Mallat塔式算法逐层分解计算带噪的小波变换系数，如图1。分解后信号的小波系数（Cd）大于噪声的小波系数（Ca），然后通过设定的阈值分离两种系数，保留大于阈值的信号小波系数，置零小于阈值的噪声小波系数，从而达到去噪的目的。小波阈值去噪基本流程如下：首先，通过选择合适的层数和小波基对噪声信号进行分解，得到小波系数wj，k；其次，选择合适的阈值，利用阈值函数对各层系数进行量化，得到小波估计系数＾wi，j；最后，通过重构小波估计系数得到去噪后的信号。

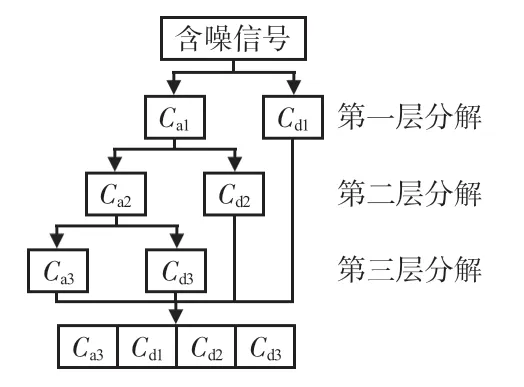
图1 小波变换示意

2 改进小波阈值函数

2.1 改进阈值函数推导

本文提出一种改进的小波阈值函数，表达式为

式中λ为阈值，wj，k为分解后得到j层第k个小波系数，为wj，k估计的小波系数。

该阈值函数具有以下特点：

1）连续性：

当wj，k→λ时

可知，改进阈值函数在wj，k→λ时是连续的。

同理，当wj，k→-λ时

可知，改进阈值函数在wj，k→-λ时是连续的。

因此，改进阈值函数在阈值处是连续的。

2）渐进性：

当wj，k→+∞时

同理，当wj，k→-∞时

因此，使用本文构造的改进阈值函数处理后的小波估计系数无限逼近于处理前的小波系数，减小了恒定偏差。

改进阈值函数与两种传统阈值函数图像对比如图2所示。

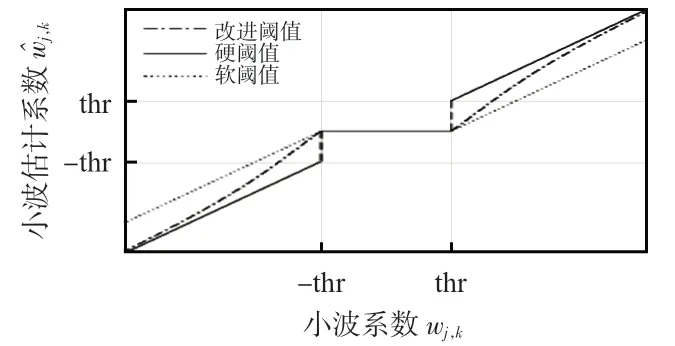
图2 改进阈值函数、软／硬阈值函数对比

2.2 改进阈值函数仿真与分析

本文通过仿真软件设计了一个原始信号并且添加高斯白噪声进行仿真。原始信号及含噪信号的表达式如下

式中 NoiseSignal（t）为含噪信号，Signal（t）为原始信号，GaussianNoise（t）为高斯白噪声，Coe为噪声的比例系数。

原始信号公式中，前面一段模拟了姿态传感器静止不动的情况，后面两段模拟姿态传感器运动时候的情况。原始信号和含噪信号如图3所示。

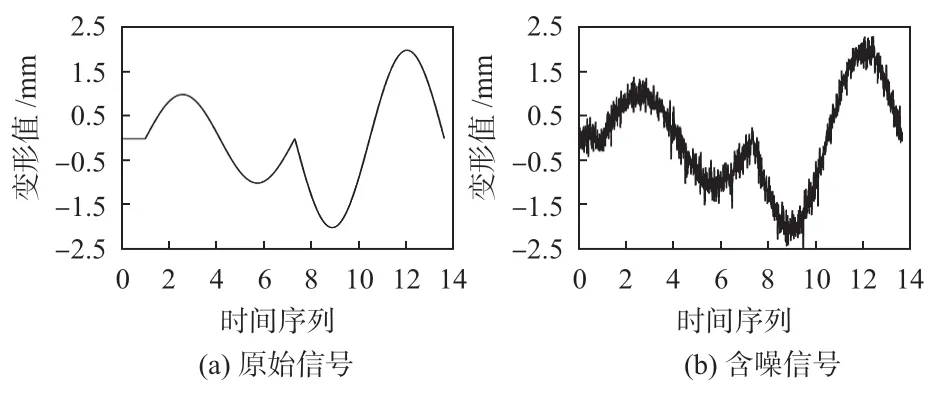
图3 仿真信号

对于含噪仿真信号分别用传统的软硬阈值函数和改进阈值函数进行去噪分析，其中小波基选取去噪效果较好且具有更好的正则性与对称性的SymN 函数，分解层数为5层，去噪阈值选择为固定阈值。处理后的数据如图4 所示。从图4 中可以看出，改进阈值函数去噪效果在信号整体平滑度和精度上都有明显提升。

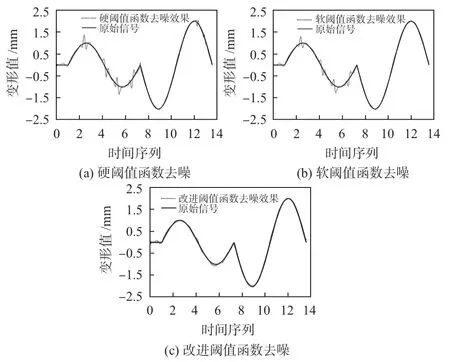
图4 去噪效果对比

信号去噪效果评估通常采用信噪比（SNR）与均方根误差（RMSE）来量化分析［16～18］。SNR和RMSE的定义为

式中Psig为不含噪声原始信号的功率，PN为噪声的功率，Nsig为含噪信号，sig为不含噪声的原始信号，N为信号的长度。

对3种阈值函数处理后的数据分别计算信噪比与均方根误差，结果如表1 所示。由表1 可以看出，3 种阈值函数处理后的信噪比，相比未处理前都有明显提高，其中改进阈值函数提升效果最好；均方根误差也是改进阈值函数处理后的数值更小。仿真结果表明，本文提出的改进阈值函数能够在保留原始信号特征的基础上，有效抑制重构信号振荡。

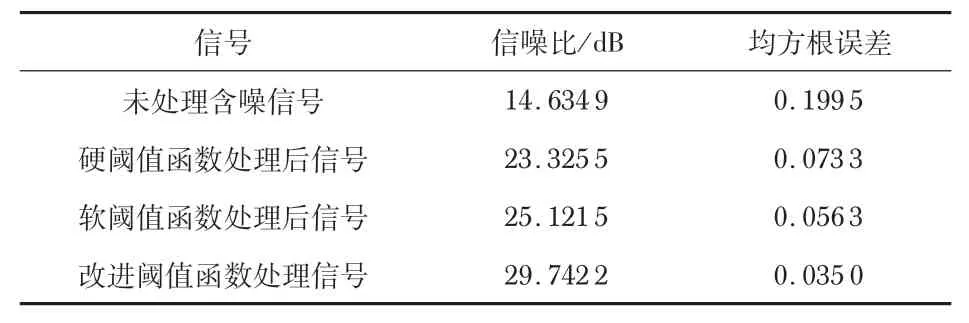
表1 降噪效果对比

3 实验验证

3.1 实验方案

由于仿真信号添加的噪声较为单一，而实际工作环境所含有的噪声较为复杂且无规律［19］，现通过将改进阈值函数应用于手部康复系统中以进一步验证其去噪能力。

如图5所示，所设计的手部康复系统主要由数据手套、数据采集模块、控制模块、上位机、交互软件等部分组成，针对处于康复中后期手指关节已经有了一定的力量与灵敏度的患者可协助进行灵敏度训练［20］。患手穿戴手套训练时，首先模拟抓取小球，然后手腕翻转一定角度将小球抛出来锻炼手指、手腕的关节活动度。传感器采集患者手部运动姿态、手指弯曲度等数据传输给控制模块，通过串口发送给上位机。上位机中交互软件解码传感器数据控制虚拟场景变化，实现真实手与交互软件中虚拟手的运动映射，进行小球抓／抛运动的可视化。同时，系统记录训练数据，为医生指导患者训练提供客观依据。

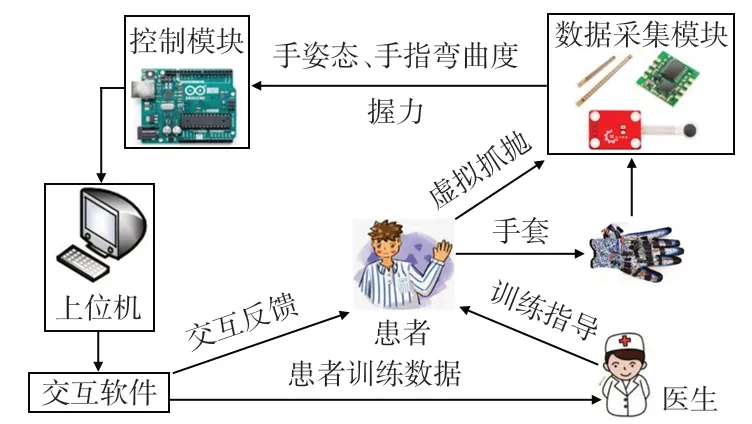
图5 实验方案设计

3.2 系统搭建与实现

本文手部康复系统所使用的数据手套如图6 所示。数据采集模块采用Jy61 姿态传感器和Flex2.2 弯曲度传感器，控制模块采用Arduino开发板。上位机系统硬件配置为Intel®CoreTMi7-8700处理器，CPU 主频为3.2 GHz，运行内存4 GB，显卡为NVIDIA GeForce GT730。交互软件系统采用Windows 10平台，利用Unity 3D搭建手部灵敏度康复训练场景，模型构建使用3Dmax。开发语言为C＃，主要用于算法编写，并实现系统与数据手套的串口通信。

图6 数据手套

为测试改进阈值函数去噪效果的有效性，在完成康复系统调试后，测试者穿戴数据手套，与场景中虚拟手进行交互，通过真实人手模拟抓抛球运动，带动虚拟手抓抛场景中的虚拟小球，如图7。

测试实验发现，虚拟手对真实手动作同步性良好，无明显延迟，并且动作平稳顺畅，基本避免了虚拟手因环境噪声产生的抖动。实验结果表明：本文构造的改进小波阈值函数可有效消除手部姿态获取过程中的噪声并与实际特征数据相契合。

4 结束语

本文提出了一种改进小波阈值函数，在不额外添加调节参数的前提下，解决传统阈值函数不连续、失真等问题。通过仿真软件对添加高斯白噪声的数据信号进行去噪，结果表明：改进阈值函数去噪效果更佳，其信噪比和均方根误差相比软硬阈值函数都有明显的优势，均方误差小，峰值信噪比大。

将改进阈值函数搭载在手部康复系统的数据手套上，对姿态传感器（Jy61模块）信号进行去噪实验，验证了方法的有效性。算法可有效提高手部姿态、手指弯曲度等信息获取精度，以及系统映射的实时性，具有良好的实际应用价值。