基于终端角度约束的鱼雷滑模制导律

马雪飞，王 智，宋清华，吴英姿，陶 鹏，师豪杰

（1.哈尔滨工程大学 信息与通信工程学院，哈尔滨 150001；2.中国电子科技集团公司第二十八研究所，南京 210007；3.武汉第二船舶设计研究所，武汉 430064；4.哈尔滨工程大学 水声工程学院，哈尔滨 150001；5.中国舰船研究设计中心，武汉 430064）

作为现代海洋战争中最重要的精确制导武器之一，鱼雷已经成为各国海洋军事力量发展的重要方向。鱼雷制导律将直接影响鱼雷命中目标精度和毁伤能力，是实现鱼雷精确打击的关键技术之一。随着海战环境的日益复杂和水声对抗技术的不断发展，现代海战中鱼雷的突防和攻击目标面临着越来越大的挑战。为了提升鱼雷对目标的打击能力和毁伤效果，需要鱼雷以一定的角度命中目标，针对水面舰艇的薄弱部件进行打击，以此提升鱼雷的毁伤力度，满足现代制导武器精确打击的要求。

自文献[1]在1973 年首次提出了一种基于落角约束的导引律，将角度约束控制引入制导律的设计之中[1]，具备终端角度约束的制导律经过研究已取得一定的研究成果[2-6]。文献[7]将最优控制理论引入飞行程序设计之中[7]。随着现代控制理论的发展，滑模控制因其非线性特性、快速收敛性和强鲁棒性等优点被常用于制导律的设计之中[8-15]。文献[8]基于滑模控制理论提出了一种切换制导策略满足撞击角度和撞击时间终端的约束[8]。文献[9]提出了一种基于时基发生器函数的时变滑模控制方法，该方法可以保证截获时刻视线角收敛到期望值的小邻域内[9]。文献[10]针对打击角度和打击时间约束制导问题，设计一种不需要估计剩余飞行时间的非奇异终端滑模寻的制导律[10]。文献[11]针对传统滑模趋近律在末端制导中存在收敛速度慢、消耗时间长及抖振现象严重等缺点，提出了一种使用双幂次趋近律的导弹终端滑模制导方法[11]。文献[12]和文献[13]将滑模控制理论与时间控制约束结合进行研究[12,13]。文献[14]针对机动目标拦截过程中加速度信息难以获取的实际问题，设计了一种基于RBF 神经网络的自适应滑模拦截制导律，有效提高了导弹制导系统的鲁棒性能[14]。文献[15]为实现对运动目标的精确打击，以脱靶量与终端落角为约束条件，提出了一种全局复合滑模制导律，运用饱和函数取代滑模制导中的符号函数削弱了系统抖振[15]。以上制导律的研究均包含落角约束或含时间和角度约束打击静止目标或运动目标，但未考虑制导律的抗干扰性和脱靶量的问题。

基于上述分析，本文提出一种偏置比例滑模制导律，满足终端角度约束的同时具备抗干扰性和较小脱靶量。首先建立鱼雷与目标的二维平面运动模型，将滑模控制与偏置比例导引结合，并基于Lyapunov 函数稳定性理论证明制导律的稳定性，最后根据不同的初始条件进行仿真对比分析，设计的制导律不仅能精确实现命中目标的同时还具备较小的角度误差和脱靶量最优的优点，验证该制导律的可行性和有效性。

1 鱼雷与目标相对运动模型

为了鱼雷能准确攻击到目标，一般在设计制导律时，只要控制鱼雷和目标的相对视线角变化率在末制导结束之前收敛到零或者零附近，鱼雷就能够成功击中目标。为简化研究做如下假设：

1) 鱼雷与目标均为质点，忽略鱼雷与目标的形状、质量和环境干扰。

2) 鱼雷与目标的运动速度大小保持不变。

3) 鱼雷的导引和控制系统为理想系统，没有响应延迟。

4) 只考虑鱼雷与目标的二维平面运动。

在二维平面内建立鱼雷与目标的相对运动关系如图1 所示。以二维平面作为参考，在该平面内以x轴为水平参考线，M表示鱼雷，T代表目标，R表示鱼雷-目标之间的相对距离，q为视线角是鱼雷-目标之间的相对视线与水平面之间的夹角，θM表示鱼雷的航向角（弹道倾角），θT表示目标的航向角，φM、φT分别表示鱼雷和目标的前置角，aM、aT分别表示鱼雷目标的法向加速度，VM、VT分别表示鱼雷和目标的速度。

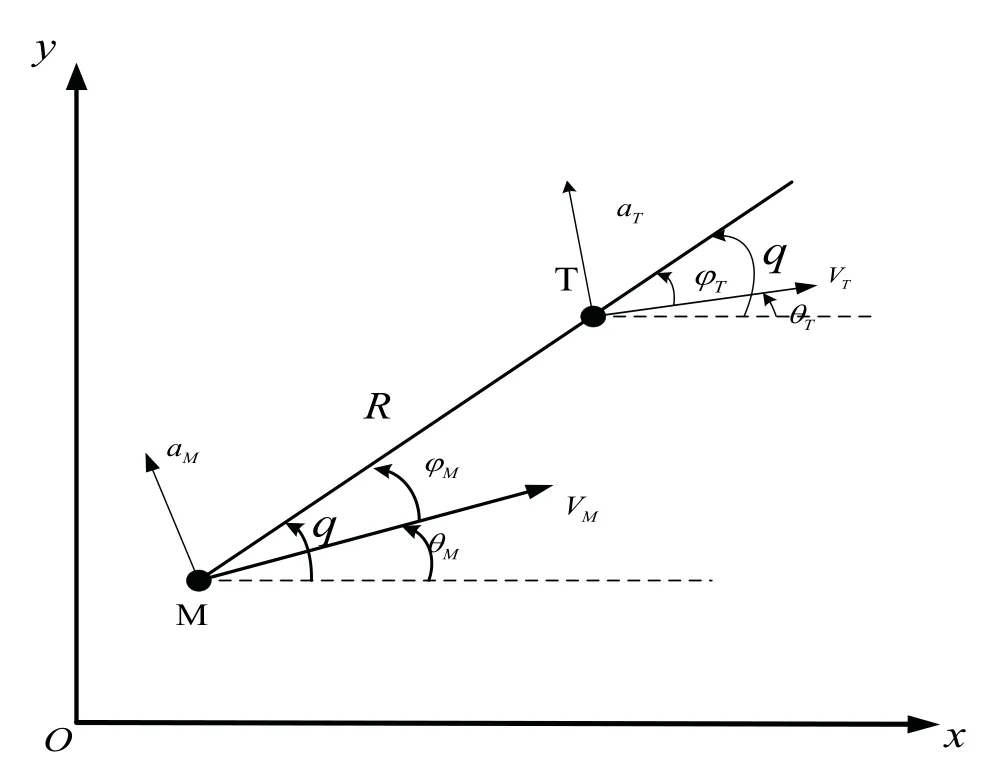
图1 鱼雷与目标相对运动模型Fig.1 Relative motion model between torpedo and target

由图1 可知，将鱼雷和目标的速度方向分别沿视线方向及法线方向进行分解，其中沿视线分量VMcos（q-θM）指向目标，可使相对距离减小；而分量VTsin（q-θM）背离鱼雷，可使相对距离增大。有：

沿视线法线的分量VTsin（q-θT）使视线绕原点逆时针旋转，可使视线角减小；沿视线法线的分量VMsin（q-θM）使视线绕原点逆时针旋转，可使视线角增大。根据图1 有式(2)成立：

由式(1)(2)可得，在二维平面内鱼雷与目标的相对运动方程为：

2 基于终端角度约束的鱼雷滑模制导律设计

2.1 制导律滑模面设计

以鱼雷法向加速度为制导指令，偏置比例导引律的形式为：

其中，第一项为比例导引的基本形式，满足在N≥ 2末端制导时刻保证鱼雷命中目标，第二项为偏置项，是为了控制鱼雷终端角度约束。

通过式(3)(4)可得：

对式(5)两边在区间[t1,t2］进行积分，可得：

式(6)(7)中，θM2和q2分别为t2时刻鱼雷的航向角和雷目视线角；θM1和q1分别为t1时刻鱼雷的航向角和雷目视线角。

将当前时刻t和终端时刻tf代入式(7)可得：

其中，θMf为命中目标时鱼雷的航向角，qf为终端雷目视线角。为了满足终端落角约束，希望鱼雷航向角满足θM-θMf→ 0，同时视线角满足q-qf→ 0。命中目标时，鱼雷前置角为零，即θMf＝qf，因此可得：

因此根据滑模变结构控制原理和终端条件，滑模面s选取为：

由式(10)可知，当s趋近于零时，鱼雷将以期望的攻击角度θMf击中目标。

2.2 幂次趋近律设计

为了保证鱼雷所设计的制导律在制导过程中具备良好的品质，需要考虑合适的趋近律来指定滑模控制切换的策略。考虑如下幂次趋近律：

其中，k为趋近律系数，α表示趋近律可调参数，通过改变α值可以改变系统的趋近速率，该幂次趋近律满足系统在趋近切换面时获取较大的趋近速率，但远离滑模面时趋近速率较慢，因此需要进行幂次趋近律改进[11]：

式(12)中，k1,k2为趋近速率系数，符号函数表达式为：

2.3 滑模制导律设计

根据所设计的切换面和趋近律函数可得滑模制导律的最终表达式。对式(10)进行微分可得：

结合式(3)(12)(14)可得基于终端角度约束的鱼雷滑模制导律的表达形式为：

式(15)中，α是趋近律可调参数，N为比例系数，k1,k2为趋近律系数。

2.4 稳定性分析

滑模动态存在的数学表达式为：

上式表明在切换面s领域内，系统将在有限时间内到达切换面。式(16)也可改写为全局到达条件形式：

由式(18)可知，当且仅当s≠ 0时，V＞ 0且V˙。由Lyapunov 函数稳定性可知，设计的制导系统是稳定的。

2.5 消除抖动方法

考虑到制导律表达式(15)中含有符号函数sgn(s)，而符号函数的不连续性会导致系统抖动，为了减小或削弱符号函数造成的系统抖动，可采用饱和函数或双曲正切函数代替符号函数，提高系统的抗干扰能力。双曲正切函数表达式：

将式(19)代入式(15)可得消除抖动后的鱼雷滑模制导律的表达形式为：

3 仿真结果及分析

为了验证本文所提出的鱼雷终端角度约束的滑模制导律的有效性和可行性，考虑三枚鱼雷在平面内攻击一个目标的情形，鱼雷剩余时间估计采用文献[16]的方法。

考虑不同场景进行验证分析，制导指令中的可调参数α取值对角度约束影响如图2 所示，随着α增加，导致鱼雷期望攻击角度约束命中目标的时间增加，并且鱼雷的航向角的最大值产生变化，但并未影响以期望角度命中目标。因此在后续的仿真中α取0.5，趋近律系数，则k1的取值为3，k2的取值为2。

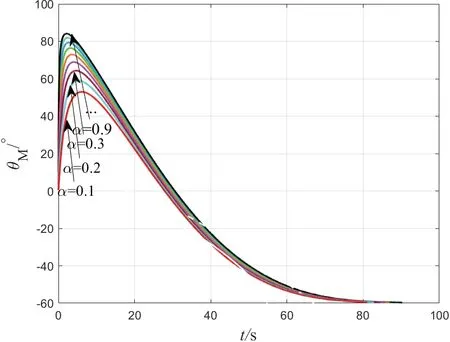
图2 可调参数α 取值对角度约束影响Fig.2 The influence of adjustable parameter α value on angle constraint

场景一：考虑鱼雷初始航向角相同，期望不同的落角约束攻击静止目标。仿真参数如表1 所示。

表1 场景一仿真参数Tab.1 Scene-1 simulation parameters

场景二：考虑鱼雷初始航向角不同，期望相同的落角约束攻击静止目标。仿真参数如表2 所示。

场景三：考虑鱼雷初始航向角相同，期望不同的落角约束攻击运动目标。仿真参数如表3 所示。

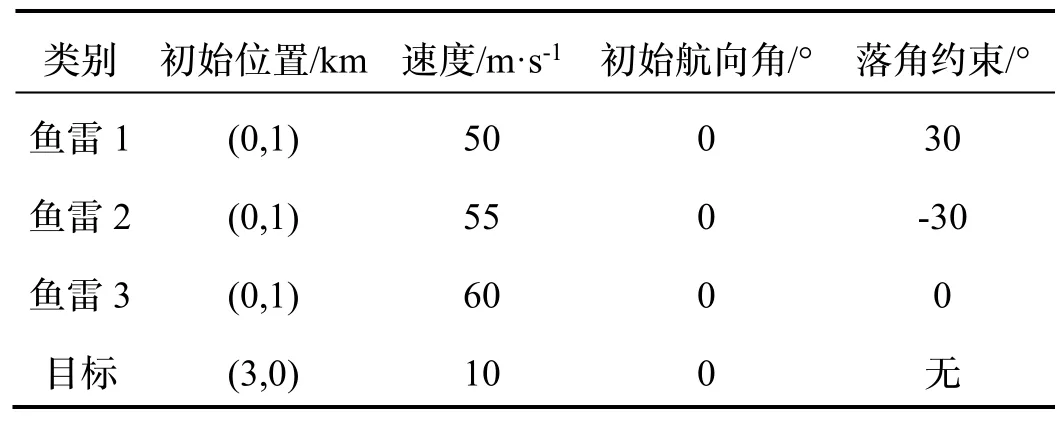
表3 场景三仿真参数Tab.3 Scene-3 simulation parameters

场景四：考虑鱼雷初始航向角不同，期望相同的落角约束攻击运动目标。仿真参数如表4 所示。

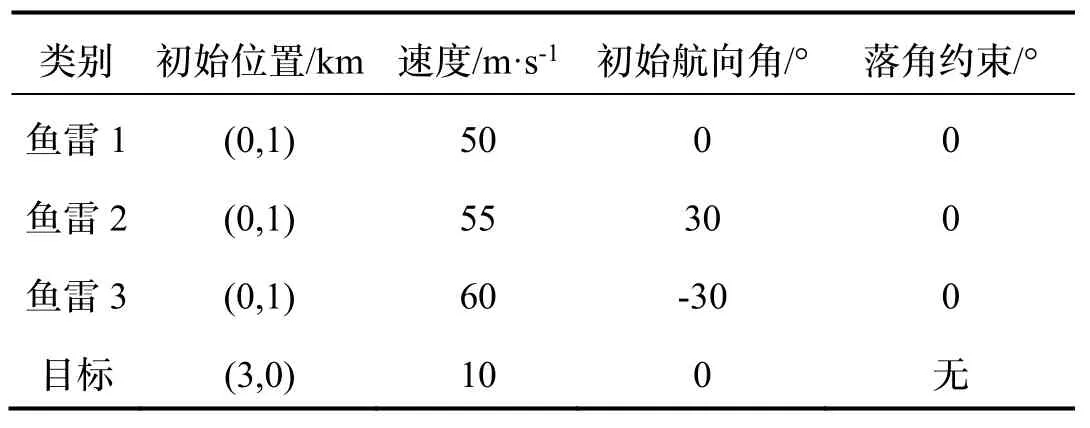
表4 场景四仿真参数Tab.4 Scene-4 simulation parameters

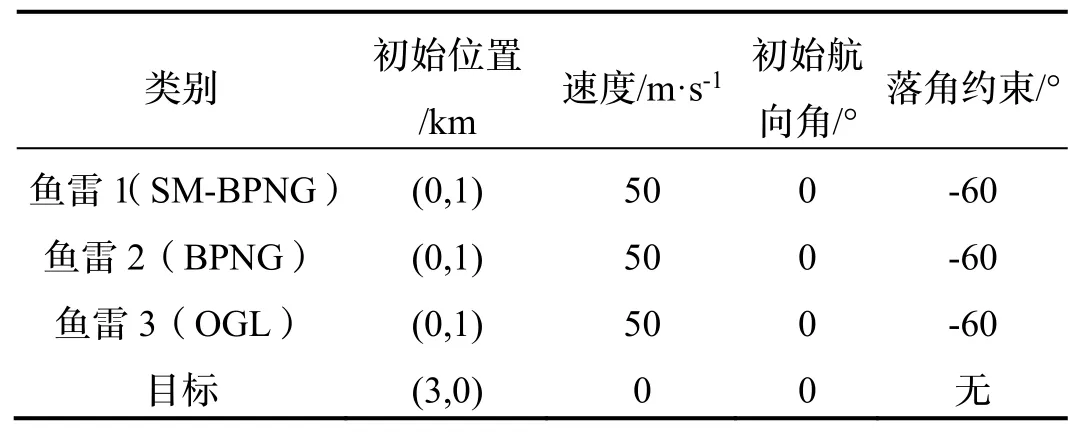
表5 场景五仿真参数Tab.5 Scene-5 simulation parameters

场景五：与文献[17]中偏置比例制导律（Biased Proportional Guidance Law,BPNG）和文献[18]中最优制导律（Optimal Guidance Law,OGL）在相同参数设置下，对比仿真分析。将本文设计的制导律（式(15)）称之为滑模偏置比例制导律（Sliding Mode-Biased Proportional Guidance Law,SM-BPNG），仿真参数如表 5 所示。

场景六：为了验证制导律的抗干扰性，考虑在式(15)制导律中加入模拟噪声干扰，仿真参数如表6 所示。

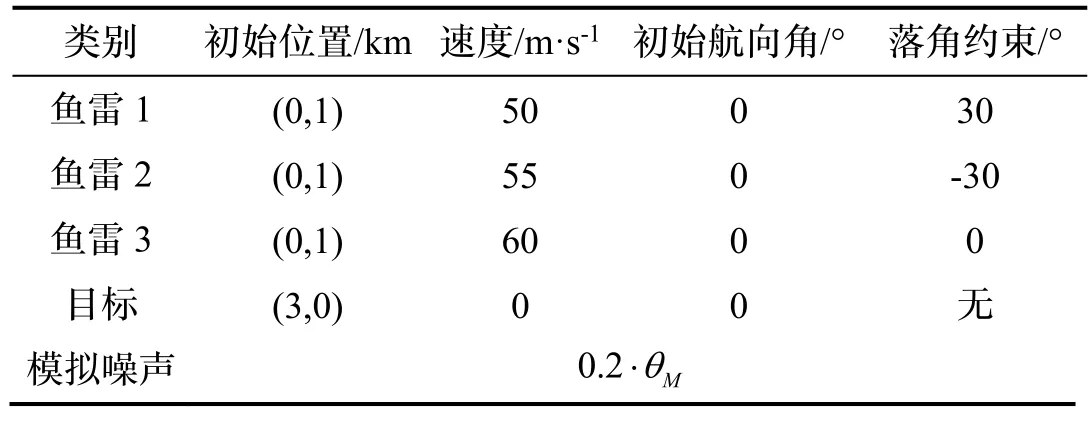
表6 场景六仿真参数Tab.6 Scene-6 simulation parameters

图3 表示场景一的仿真结果。由图3(a)和图3(b)可知，当目标处于静止状态下，三枚鱼雷在不同时刻下命中目标。由图3(c)可知，三枚鱼雷按照各自预定的攻击角度-60 °、-45 °和0 °完成击中目标的任务，该制导律可以实现期望落角约束，保证制导精度。由图3(d)可知，三枚鱼雷的需用法向过载指令曲线变化较为平稳，前半段能充分发挥鱼雷的机动能力，在4.9 s 就趋近于零，且过载也在可用范围之类。具体仿真结果如表7 所示。

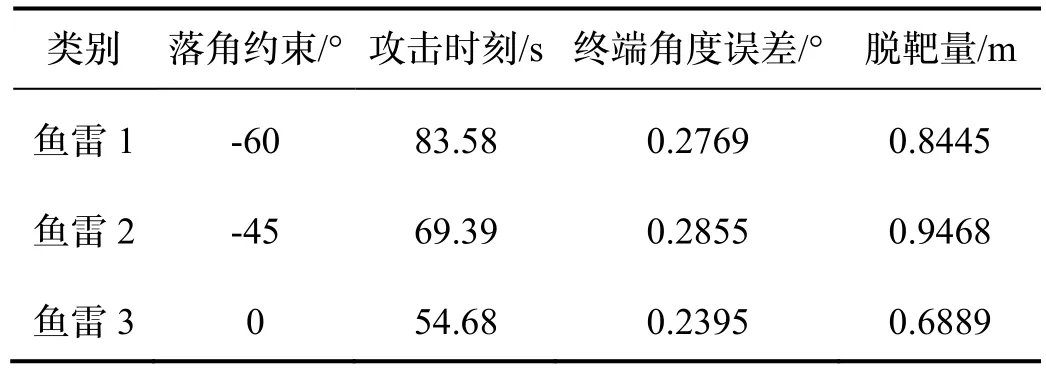
表7 仿真结果Tab.7 Simulated results

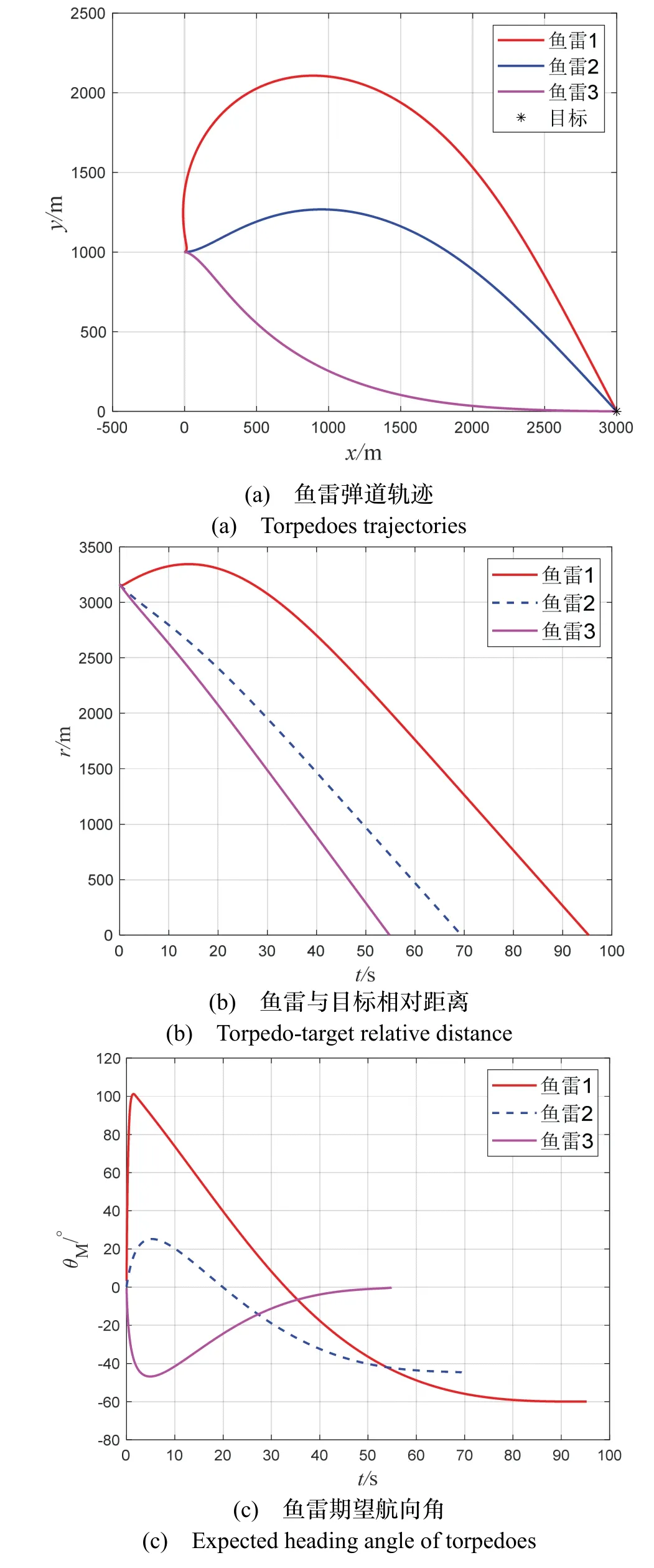
图3 场景一仿真结果Fig.3 Simulated results of scenario 1

图4 表示场景二的仿真结果。由图4(a)和图4(b)可知，当目标处于静止状态下，三枚鱼雷在不同时刻下命中目标。由图4(c)可知，三枚鱼雷按照各自预定的攻击角度-60 °完成击中目标的任务，该制导律可以实现在初始航向角不同的情况下实现期望落角约束，保证了制导精度。由图4(d)可知，三枚鱼雷的需用法向过载指令曲线变化较为平稳，前半段能充分发挥鱼雷的机动能力，在2.1 s 就趋近于零了，法向过载也在可用范围之类，保证了鱼雷能以期望的攻击角度击中目标。具体仿真结果如表8 所示。

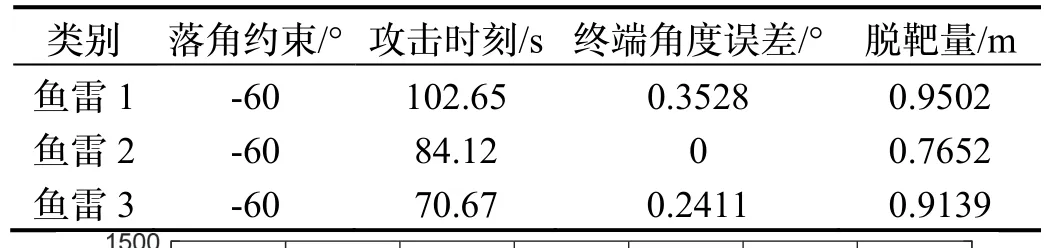
表8 仿真结果Tab.8 Simulated results

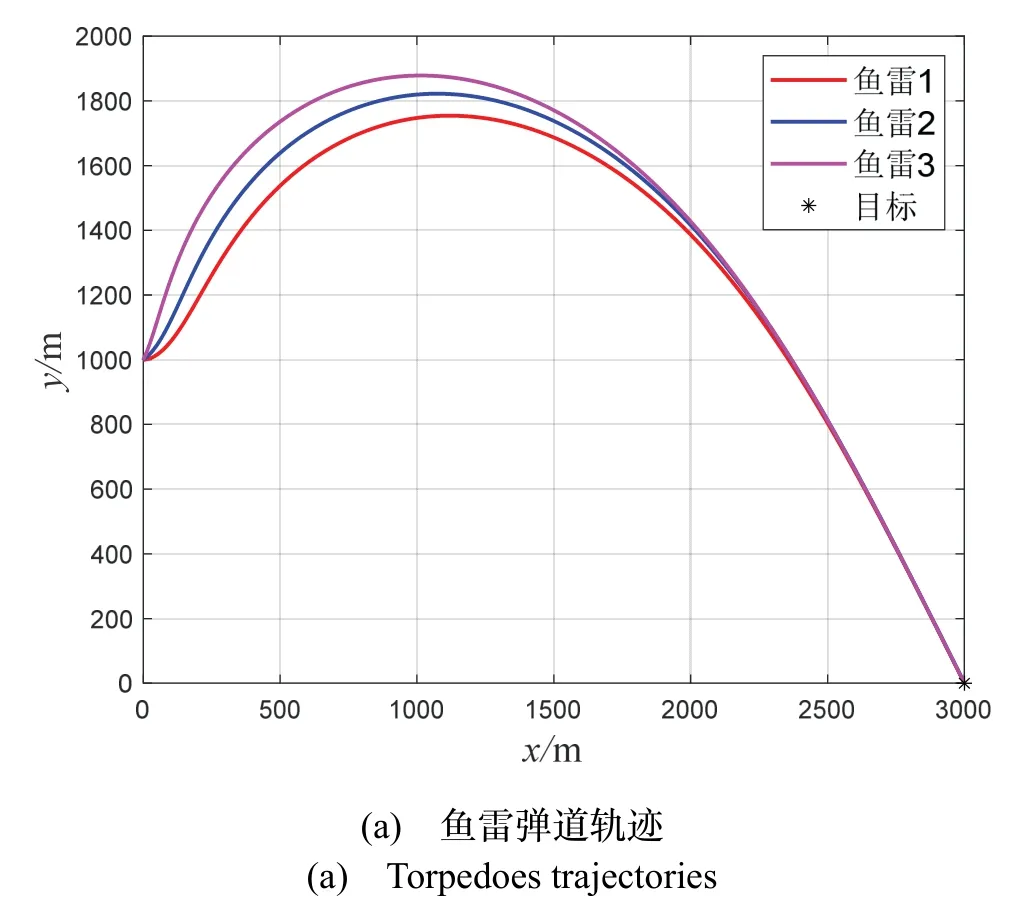
图4 场景二仿真结果Fig.4 Simulated results of scenario 2

图5 表示场景三的仿真结果。由图5(a)和图5(b)可知，当目标处于匀速直线运动状态下，三枚鱼雷在不同时刻下命中目标。由图5(c)可知，三枚鱼雷按照各自预定的攻击角度30 °、-35 °和0 °完成击中目标的任务，该制导律可以实现期望落角约束。由图5(d)可知，三枚鱼雷的需用法向过载指令曲线变化较为平稳，前半段能充分发挥鱼雷的机动能力，在7.01 s 就趋近于零了，且过载也在可用范围之类。具体仿真结果如表9 所示。

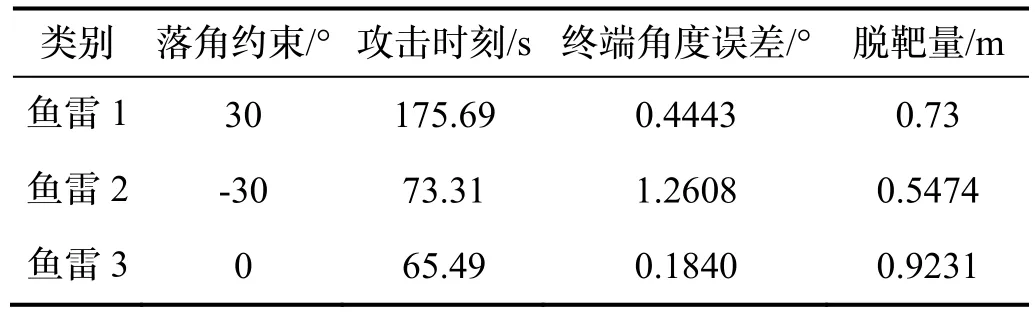
表9 仿真结果Tab.9 Simulated results

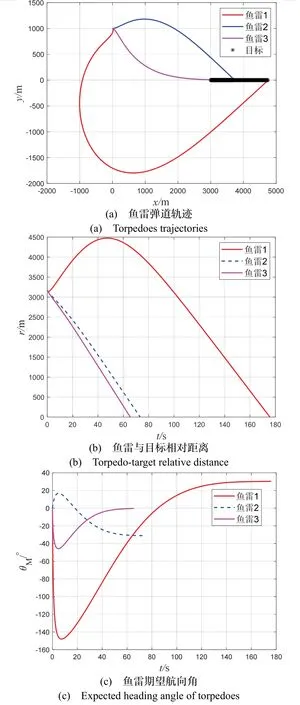
图5 场景三仿真结果Fig.5 Simulated results of scenario 3

图6 表示场景四的仿真结果。由图6(a)和图6(b)可知，当目标处于匀速直线运动状态下，三枚鱼雷在不同时刻下命中目标。由图6(c)可知，三枚鱼雷按照各自预定的攻击角度0 °完成击中目标的任务，该制导律可以实现期望落角约束。由图6(d)可知，三枚鱼雷的需用法向过载指令曲线变化较为平稳，在26.12s 就趋近于零了，且过载也在可用范围之类，该制导指令无抖动现象。具体仿真结果如表10 所示。

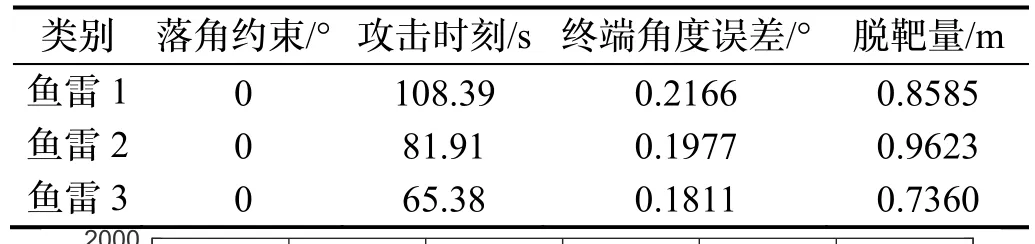
表10 仿真结果Tab.10 Simulated results

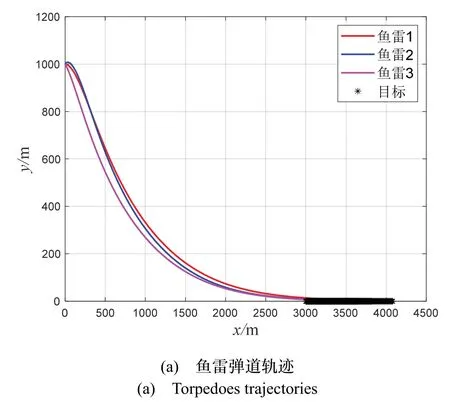
图6 场景四仿真结果Fig.6 Simulated results of scenario 4

图7 表示场景五的对比仿真结果。图7(a)表示三种制导律作用下鱼雷的弹道轨迹，其中红线表示SM-BPNG，蓝线表示BPNG，粉线代表OGL，由图 7(a)和图7(b)可知，当目标处于静止状态下，三种制导律作用下的鱼雷均能在不同时刻下命中目标。由图7(c)可知，三种制导律作用下的鱼雷按照各自预定的攻击角度-60 °完成击中目标的任务，三种制导律均可以实现期望落角约束。图7(d)表示三种制导律作用下的鱼雷制导指令曲线，只有SM-BPNG 可以前期充分发挥鱼雷机动能力，在6.5 s 左右趋近于零，该制导指令无抖动现象，充分发挥了SM-BPNG 的稳定性，提高了鱼雷的制导精度。综上所述，本文设计的制导律能满足落角约束，制导指令无抖动现象，具有良好的制导性能。三种制导律的具体仿真结果如表11 所示，在三种制导律作用下，本文设计的SM-BPNG 脱靶量相对较小，具备较小脱靶量的优点得到验证。

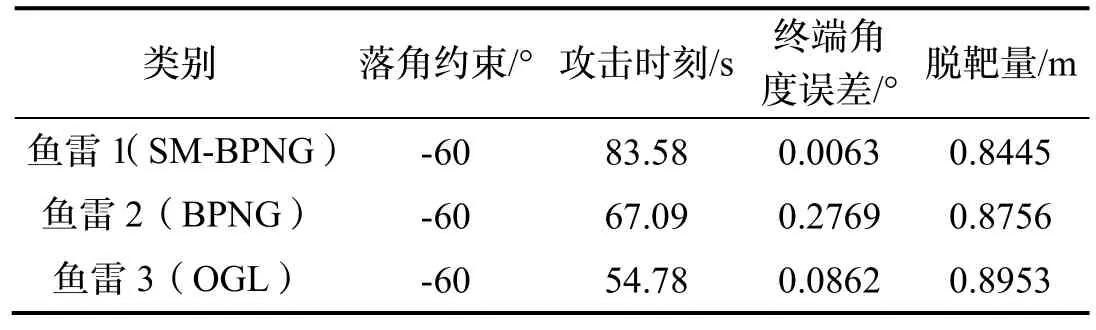
表11 仿真结果Tab.11 Simulated results

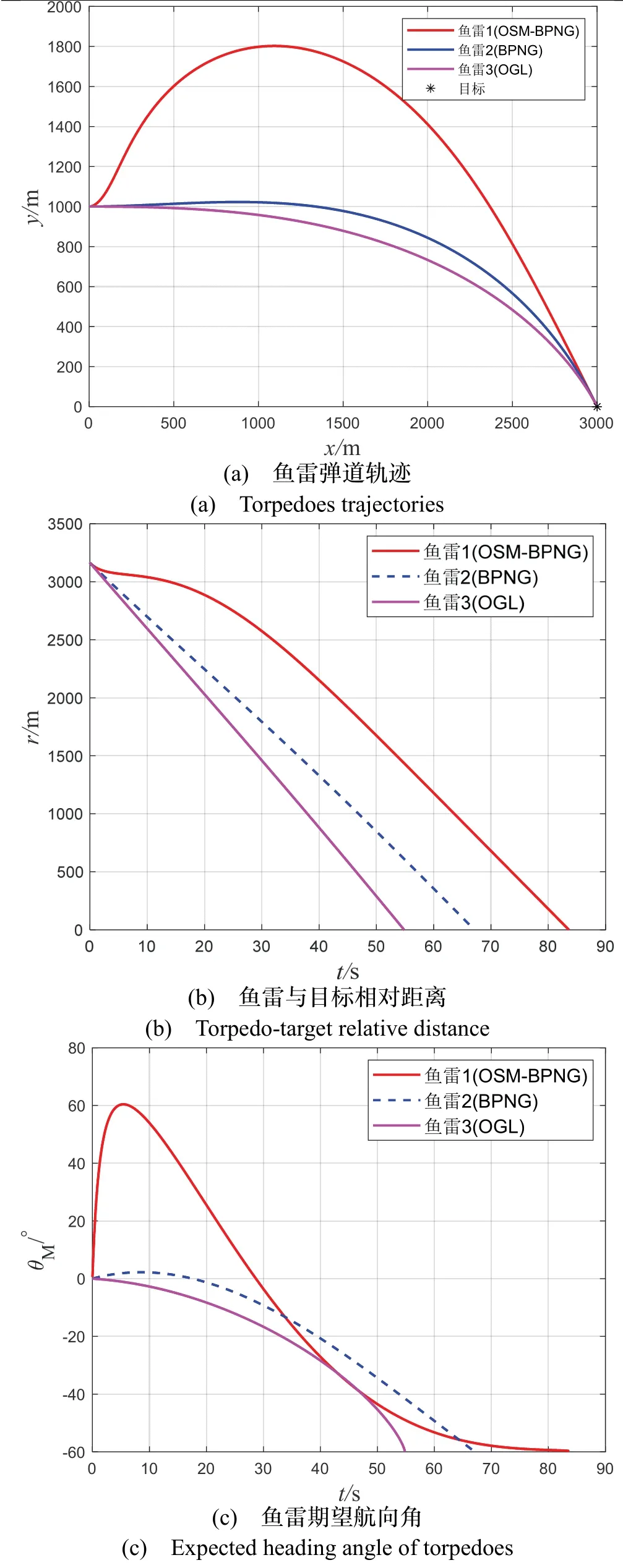
图7 场景五仿真结果Fig.7 Simulated results of scenario 5

图8 表示场景六在制导律式(15)中加入模拟噪声干扰的仿真结果。由图8(a)(b)可知，当目标处于静止状态下，加入噪声数值的制导律作用下的鱼雷均能在不同时刻下命中目标。由图8(c)可知，加入模拟噪声数值干扰情况下，鱼雷均能按照预期的角度约束30 °、-30 °和0 °完成约束要求命中目标。图8(d)为鱼雷制导指令曲线，所设计的滑模制导律在初始时刻能获取更高的法向加速度，在噪声干扰下的落角误差小于0.5 °，前期充分发挥鱼雷机动能力，在6.25 s 左右趋近于零，该制导指令并无抖动现象，充分发挥了SM-BPNG 的稳定性，提高了鱼雷的制导精度，制导指令曲线在末端时刻能快速收敛为零。具体仿真结果如表12 所示，在添加噪声的情况下该制导律的抗干扰性及稳定性得到了验证。

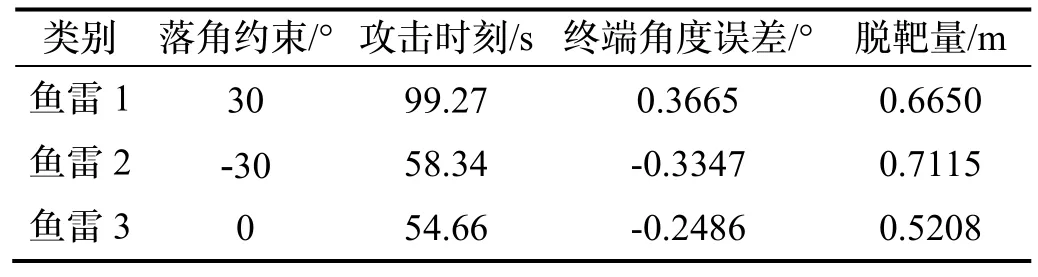
表12 仿真结果Tab.12 Simulated results

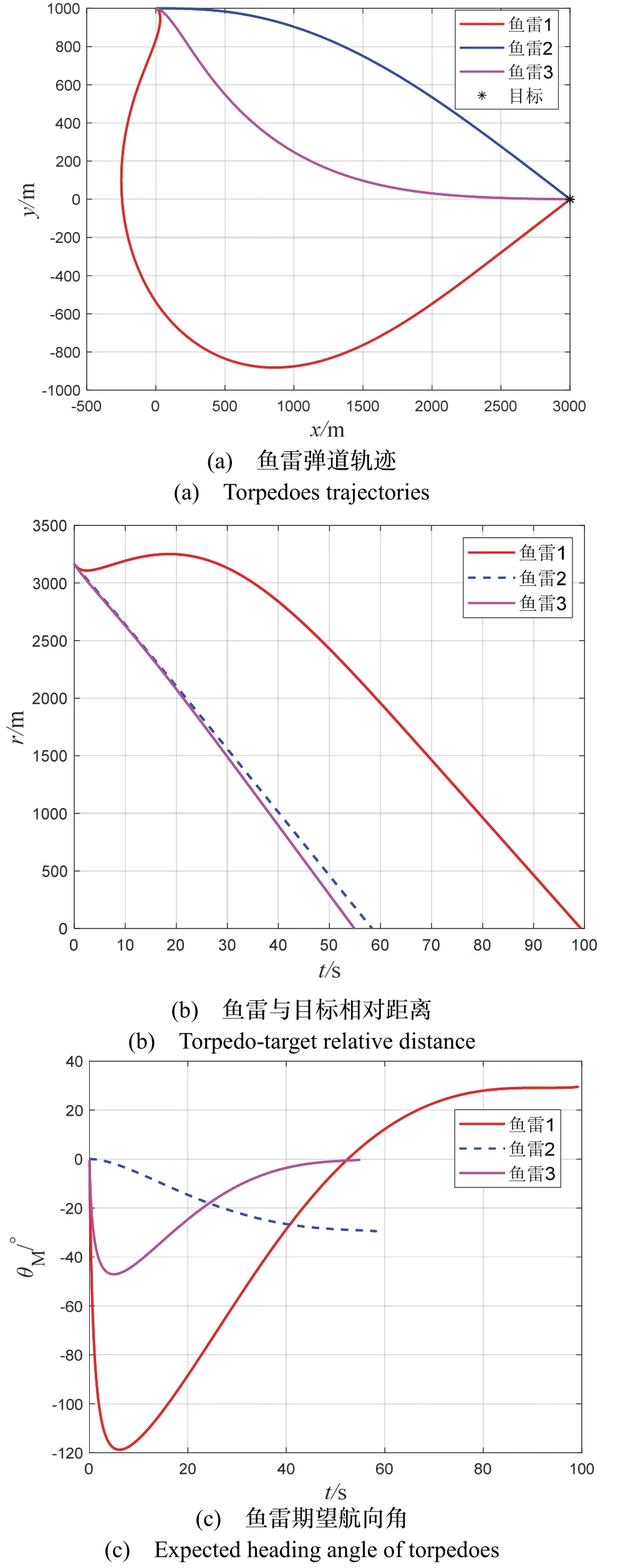
图8 场景六仿真结果Fig.8 Simulated results of scenario 6

4 结论

本文对终端角度约束的鱼雷打击目标问题进行了研究，首先建立鱼雷与目标的二维平面运动模型，推导了基于偏置比例导引的滑模制导律，并验证Lyapunov 函数的稳定性，最后根据不同的初始条件进行不同场景的仿真分析。仿真结果表明，在静止或运动状态下，设计的滑模制导律能以期望的终端角度约束精确命中目标的同时，保持弹道曲线比较平滑，脱靶量均小于1 m，在噪声干扰数值下落角约束误差小于0.4 °，制导指令在合理范围内快速收敛等优点，因此设计的滑模制导律具有良好的工程应用价值。

未来研究的重点是开展带角度约束的鱼雷时间协同制导律的研究，结合现代控制理论将鱼雷攻击时间和攻击角度约束结合完成双重约束协同制导。