复杂水下环境中自适应粒子群优化的SINS/DVL 组合导航方法

王 迪，王 冰，黄浩乾，王广才，刘锡祥，姚逸卿

（1.河海大学 能源与电气学院，南京 211100；2.湖南大学 机械与运载工程学院，长沙 410006；3.东南大学 仪器科学与工程学院，南京 210096）

海洋资源丰富，而水下机器人又是开发利用海洋资源的有效载体，同时，水下机器人高效作业离不开高精度的导航定位信息。因此，水下高精度定位是水下机器人开发的关键技术之一。目前常用的水下导航方式有捷联惯性导航系统（Strap-down Inertial Navigation System,SINS）、多普勒计程仪（Doppler Velocity Log,DVL）、水声定位系统、地球物理导航系统等[1,2]。其中，捷联惯性导航系统因其自主性高、导航信息全面，在水下导航系统中承担主要角色。由于SINS 基于积分原理，存在误差随时间累积的问题，因此，SINS 一般与其他定位方式结合使用。多普勒计程仪利用多普勒声学原理，能够实时测量载体相对于海底的速度信息，且误差不随时间累积。水声定位系统包括：长基线（Long Baseline,LBL）、短基线（Short Baseline,SBL）以及超短基线（Ultra-short Baseline,USBL）。以上水声定位系统具有精度高、误差不随时间累积的特点[3,4]。但是，水声定位系统均需要事先在水下铺设基阵，具有维护复杂，且在未知海域无法使用的问题。地球物理导航方法包括：地形匹配、地磁匹配等，此类方法需要事先建立庞大的地形、地磁数据库，需要定期更新数据库且操作复杂[5]。因此，以SINS 为主、DVL 为辅的自主式导航系统受到了水下机器人的青睐，同时也成为水下机器人组合导航系统的标配并得到广泛应用。

由于水下环境复杂，声学信号传播存在不确定性和干扰性，因此基于SINS/DVL 的鲁棒滤波算法研究迫在眉睫。文献[6]为提高复杂环境下SINS/DVL 导航精度，从组合模型角度出发，提出了基于波束信息的紧组合容错模型，同时设计了DVL 波束信息缺失处理机制，提高了复杂环境下的系统鲁棒性；文献[7][8]从信息融合算法角度出发，将Huber 鲁棒滤波算法引入到SINS/DVL 系统中，提高了对外界的抗干扰能力，并通过实验验证了该算法的优越性；文献[9]针对SINS/DVL 组合导航过程中野值干扰问题，提出了一种改进的双因子抗差自适应滤波算法，通过引入卡方检测辅助双因子自适应滤波算法，提高滤波的鲁棒性。上述方法从系统抗干扰角度入手解决了导航的鲁棒性问题，但对精度的提升存在局限性。文献[10][11]针对水下噪声复杂多变的问题，将变分贝叶斯自适应滤波算法引入到SINS/DVL 组合系统中，进一步提高了系统对外界复杂噪声的自适应性。然而，采用变分贝叶斯自适应算法，虽然在一定程度上提高了复杂环境下的导航精度，但该算法涉及较多可调节参数，在自适应方面存在一定的局限性；文献[12][13]将机器学习引入到SINS/DVL 组合导航中，解决复杂环境下导航信息失效的问题，然而，该方法在训练样本和实际使用中都存在一定局限性。

针对以上研究及存在的问题，本文以复杂环境下SINS/DVL 组合导航系统为研究对象，分别从模型和算法两个角度解决外界野值和复杂噪声干扰问题。一方面，从组合导航模型角度出发，针对组合滤波中方差估计不一致的问题，引入状态变换原理，建立了SINS/DVL 导航模型；另一方面，为提高算法的鲁棒性，在Huber 鲁棒滤波算法的基础上，分别改进噪声方差阵以及引入自适应粒子群优化算法，实现对外界复杂测量信息的鲁棒处理，进而提高SINS/DVL 导航精度。

1 水下SINS/DVL 自主导航原理

由于SINS 和DVL 都是靠自身获取载体信息，不与外界发生信息交互，因此，基于SINS/DVL 的组合导航系统具有较高的自主性，其中包括惯性测量单元（Inertial Measurement Unit,IMU）和DVL。IMU 包括三轴陀螺仪和三轴加速度计，分别用来测量载体的角运动和线运动；DVL 基于多普勒原理，能够测量载体相对于海底的三维速度信息。

图1 给出了基于SINS/DVL 的组合导航框图。在IMU 测量信息的基础上，通过捷联解算能够获取载体相对导航坐标系的姿态、速度和位置信息。将经过坐标系转换的DVL 速度与SINS 速度的差值作为卡尔曼滤波器的量测，进行更新处理，即可完成整个导航过程。

2 SINS/DVL 组合导航方法

本文针对复杂水下环境对SINS/DVL 导航系统的影响，提出一种自适应粒子群优化的SINS/DVL 导航方法，具体如图2 所示。首先，针对导航模型鲁棒性问题，使用不易受干扰的地球重力信息代替易受干扰的加速度测量信息，构建基于状态变换原理的导航模型，推导出状态方程和量测方程，提高模型的鲁棒性。其次，在Huber 鲁棒滤波算法的基础上，考虑系统噪声和量测噪声的强非线性问题，引入粒子群优化算法，实现系统噪声方差阵和量测噪声方差阵的自适应估计。设计适应度函数，提高算法对干扰噪声的处理能力。最后，在粒子群优化算法的基础上，针对权重对粒子群搜索速度和收敛性的影响，提出一种改进的惯性权重计算方法，提高粒子群算法的自适应性。

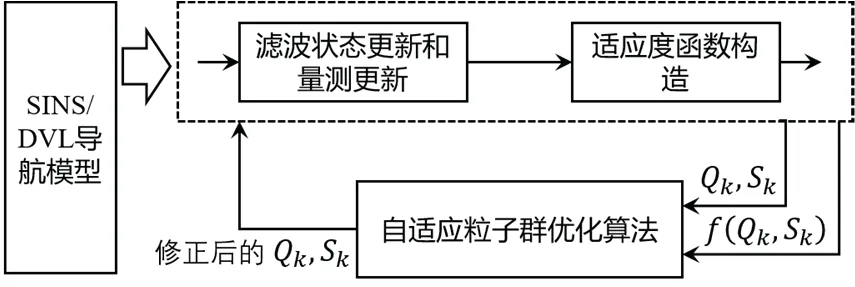
图2 自适应粒子群优化的SINS/DVL 导航方法Fig.2 Adaptive particle swarm optimization method for SINS/DVL navigation system

2.1 基于状态变换原理的导航模型

一般情况下，当地导航系下的速度微分方程为：

基于状态变换原理建立SINS/DVL 组合导航状态方程[14]：

其中，F为组合导航状态转移矩阵；W为组合导航系统噪声；X为15 维的组合导航状态向量：

组合导航状态转移矩阵由四部分组成：

其中，Mav、Maa、Map只是为了表述方便而定义的中间变量，不代表任何意义；ωie表示地球旋转角速率；L和h分别表示载体所在位置的地理纬度和高度；表示SINS 输出的速度向量；RM和RN表示载体所在位置的子午圈半径和卯酉圈半径。

从式(5)可以看出，新的速度误差微分方程对应的状态转移矩阵不再含有比力向量，而是由重力向量替代，避免了传统SINS/DVL 系统矩阵计算受动态环境下的比力fn影响，进而导致方差不一致性。

SINS/DVL 组合导航系统的量测方程[15,16]为：

其中，H表示量测转移矩阵；V表示量测噪声矩阵；Z表示量测矩阵：

SINS/DVL 组合导航系统通过DVL 速度信息修正并反馈给SINS，从而为载体提供高精度的位置信息。

2.2 滤波状态更新及噪声矩阵构造

在上述模型的基础上，进行滤波状态更新：

其中，Pk-1表示状态向量的均方误差阵；Qk-1表示k-1时刻的系统噪声方差阵。

基于Huber M估计原理，构造量测噪声方差阵Sk：

式(18)给出了量测噪声方差阵Sk的表达形式。为了能够更好地满足滤波算法对鲁棒性的需求，在上述两个噪声方差阵的基础上，引入自适应粒子滤波算法，对两个噪声方差阵进行修正，进而提高滤波的鲁棒性。此过程分为两步，粒子滤波适应度函数构造和自适应粒子群优化算法。

2.3 自适应粒子群优化处理

首先，构造适应度函数。

将系统噪声方差阵Qk和量测噪声方差阵Sk作为粒子，而SINS/DVL 组合导航系统性能主要取决于位置精度，所以将滤波器输出的位置误差均方差作为适应度函数。

其中，f（Qi,Si）是Qi,Si为参数时SINS/DVL 组合导航系统位置误差的均方差；ωˆ（Qi,Si）为估计的位置；M为估计长度；Lk为参考的实际位置值。

其次，优化自适应粒子群。

①初始化粒子群参数，在参数区间内初始化粒子群的位置和速度，随机产生若干粒子并初始化最优粒子；

② 根据上述适应度函数，对每一个粒子的适应度进行评价，比较其与最优粒子的适应度值，若适应度更好则取代最优粒子；

③粒子x＝（Qk,Si）迭代更新自己的速度和位置，每个粒子根据自身和群体经验调整轨迹向最优点靠拢，按式(20)(21)进行更新[17,18]：

为了更合理地改变惯性权重得到更优结果，对惯性权重进行改进：

其中，ustart和uend分别为惯性权重的初值和末值，取值范围为0.4≤uend≤ustart≤0 .9；IM为迭代次数的最大值；IG为当前迭代次数。

④ 重复②和③，更新最优粒子，直至满足迭代次数或精度要求，产生最优粒子。

2.4 滤波量测更新过程

在滤波状态更新和噪声矩阵修正的基础上，进行滤波量测更新：

其中，Ωk-1表示k-1时刻的状态估计权重；Ak是定义的中间变量，不代表任何意义，其具体形式为[19]：

其中，sgn(∙)表示符号函数；γ表示因子，γ＝0.8。

均方误差阵更新为：

其中，I15表示15 行15 列的单位矩阵；Kk表示k时刻的滤波增益。

3 实验分析与结果

为了验证本文方法的有效性，分别进行仿真实验和湖试实验。

3.1 仿真实验

基于MATLAB 软件开展仿真实验，其中传感器仿真参数设置为：陀螺仪零偏误差0.02 °/h，加速度计零偏误差100 μg，陀螺仪和加速度计数据输出频率为200 Hz。DVL 刻度因子误差0.003，DVL 输出频率为2 Hz。图3 给出了卡尔曼滤波方法、Huber 鲁棒滤波方法以及本文自适应粒子群优化方法的仿真运动轨迹。

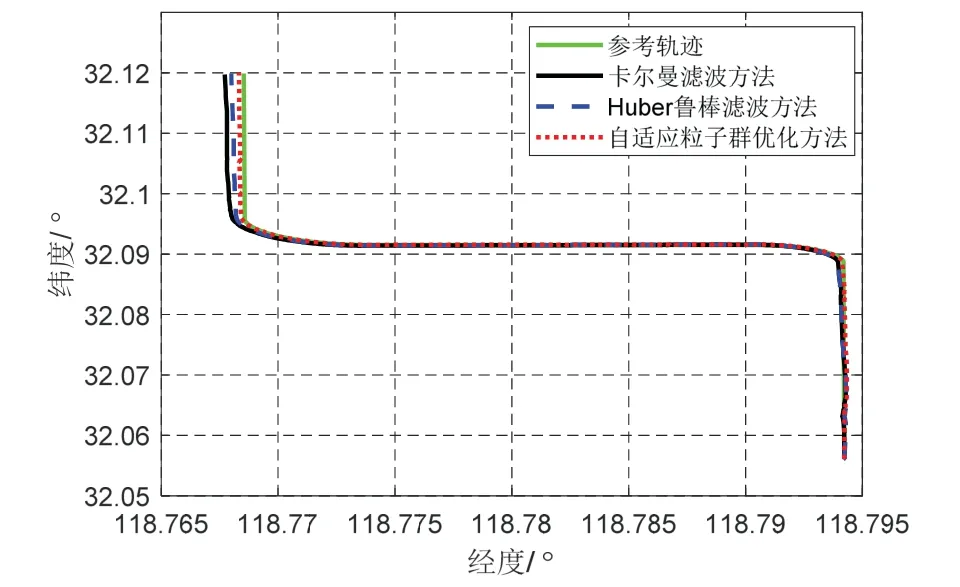
图3 仿真运动轨迹Fig.3 Simulation motion trajectories

为了能够模拟水下复杂环境对DVL 测量的干扰，在仿真参数的基础上增加噪声：

其中，RD表示设置的量测噪声方差阵表示DVL 输出的速度噪声；w.p.0.60 表示概率，即方差为原来100 倍的量测噪声以60%概率出现在原来的高斯分布中。

从图3 可以看出，三种方法的位置误差均越来越大，这是由于DVL 刻度因子误差及噪声的存在，使得SINS/DVL 导航系统误差会缓慢累积，而自适应粒子群优化方法的最终位置与参考轨迹最接近。为了更加准确地描述不同方法的定位误差，图4-5 给出了三种方法对应的SINS/DVL 组合导航系统的东向位置误差和北向位置误差。

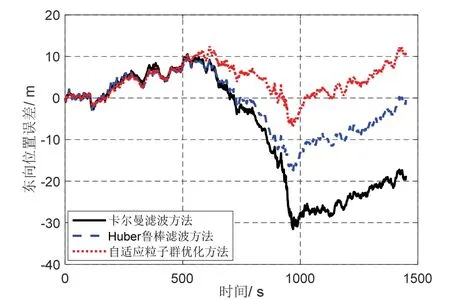
图4 东向位置误差仿真曲线Fig.4 Curves of east position error for simulation

从图4 可以看出，由于受到复杂环境干扰，卡尔曼滤波方法的东向位置误差发散最大，Huber 鲁棒滤波方法虽然一定程度上能够减少外界复杂噪声干扰，但其误差仍然比本文的自适应粒子群优化方法大。从图5 也可看出本文方法优于其他两种方法。

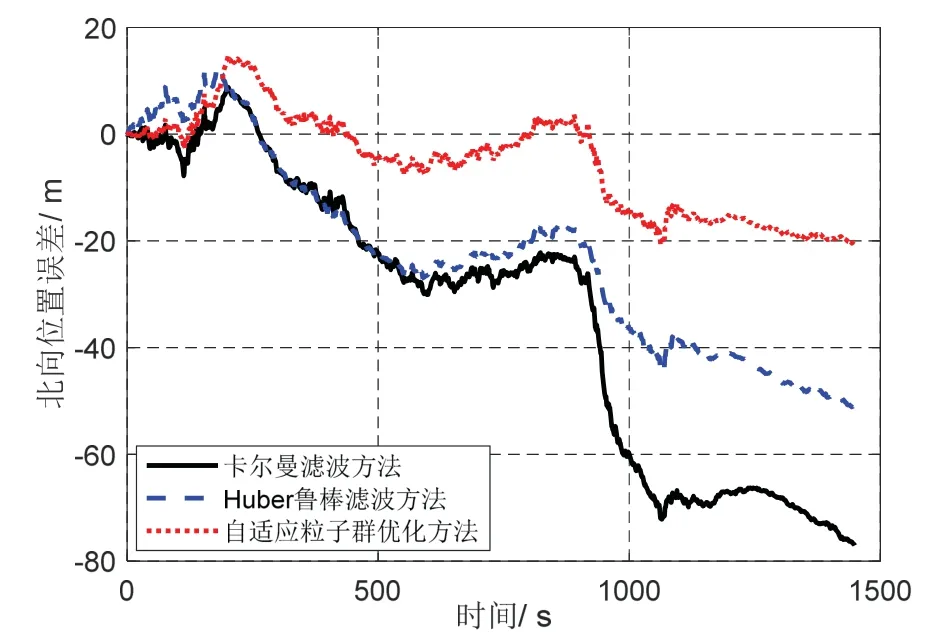
图5 北向位置误差仿真曲线Fig.5 Curves of north position error for simulation

表1 给出三种方法的位置误差绝对值的均值，表2给出三种方法的位置误差绝对值的最大值。

表2 三种方法的位置误差绝对值的最大值Tab.2 Max of position error for three methods

根据表1-2 可知，无论是位置误差均值还是位置误差最大值，本文的自适应粒子群优化方法均优于卡尔曼滤波方法和Huber 鲁棒滤波方法。

3.2 湖试实验

为验证本文方法的有效性，搭建了湖试平台。实验设备包括IMU、DVL、卫星导航系统、高精度光纤SINS、移动电源、数据采集设备、导航计算机等，如图6 所示。实验选择在江苏省盱眙县象山国家地质公园湖泊内进行，DVL 通过横跨船体的方型钢架及钢杆与船体固连，测速仪声头深入水下20 cm，在保证声头不被船底遮挡的同时还可以规避浅滩触底的风险。

图6 湖试现场图Fig.6 Lake test site photos

基准系统由RTK GPS 和高精度光纤SINS 组成，测得的高精度数据经过卡尔曼滤波算法融合后，作为参考的位姿信息。实验相关设备参数如表3 所示，其中IMU更新频率为200 Hz，DVL 更新频率为1 Hz。

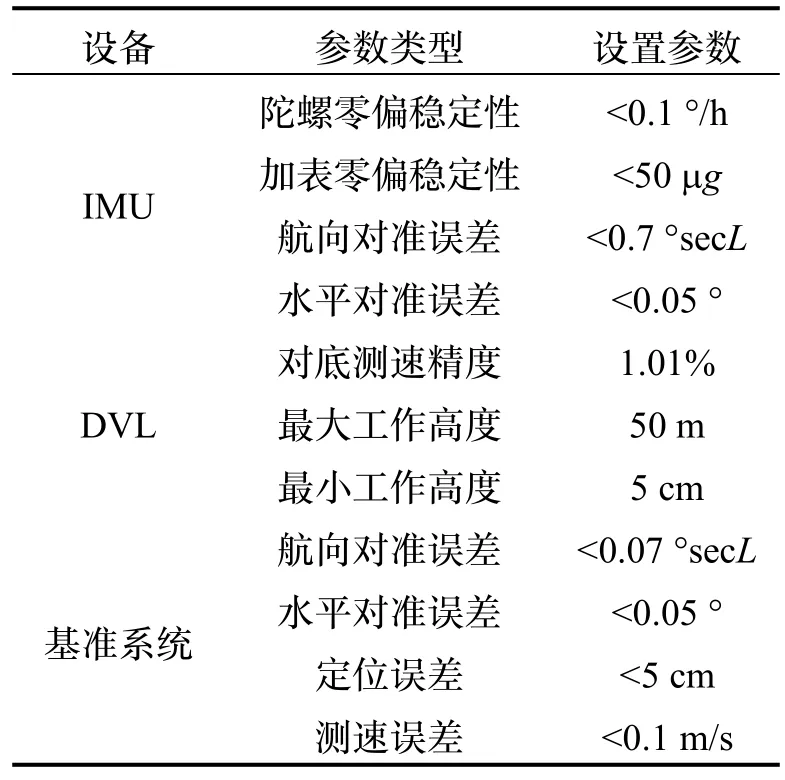
表3 实验相关设备参数Tab.3 Related equipment parameters

图7 为实验过程中载体的运动轨迹，整个运动过程持续了1050 s，包括加速、减速、转弯等各种运动。

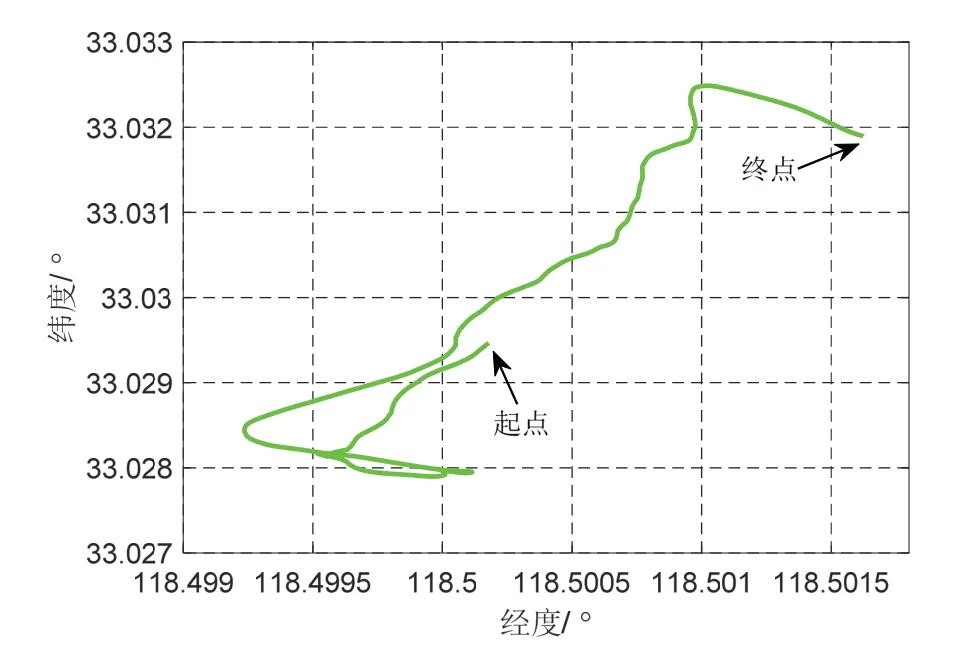
图7 湖试运动轨迹Fig.7 Motion trajectories for lake test

图8 给出了卡尔曼滤波方法、Huber 鲁棒滤波方法以及本文自适应粒子群优化方法的湖试运动轨迹。从图中可以看出，三种方法的轨迹均能紧跟参考轨迹。从局部放大图可以看出，自适应粒子群优化方法更接近参考轨迹，定位精度更高。

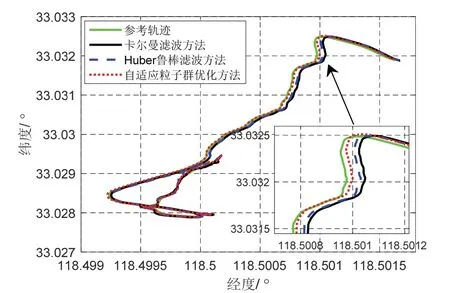
图8 三种方法的湖试运动轨迹Fig.8 Lake test motion trajectories for three methods

图9-11 给出了三种方法的东向位置误差、北向位置误差以及水平位置误差。由于高度方向一般有深度计修正，因此不再考虑高度误差。

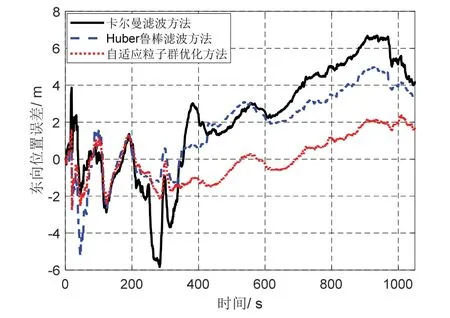
图9 湖试东向位置误差Fig.9 East position error for lake test

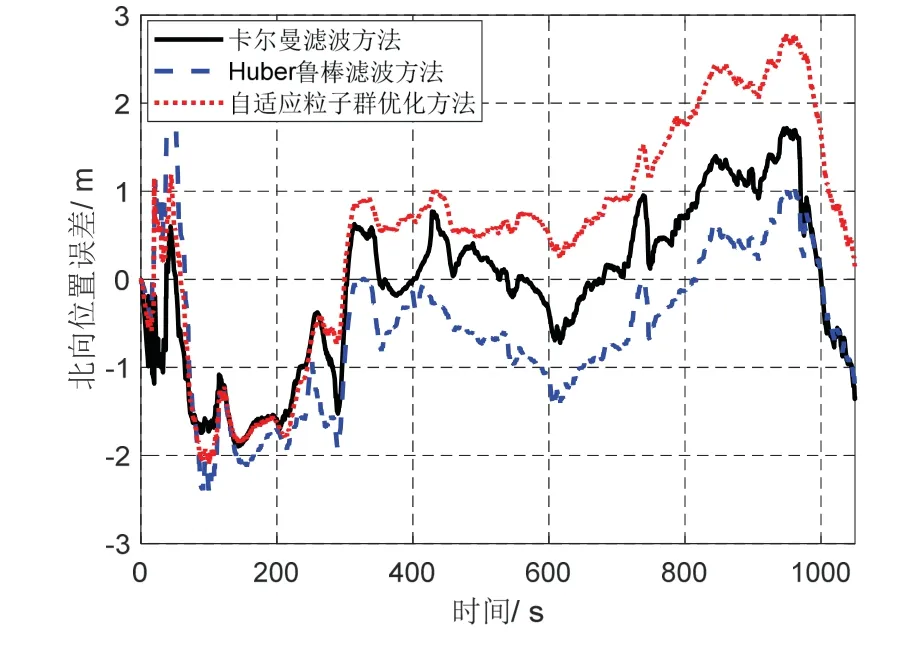
图10 湖试北向位置误差Fig.10 North position error for lake test

从图9-11 可以看出，本文方法的位置误差较小。值得注意的是在北向位置误差方面，本文方法的位置误差大于其他两种方法，这与运动轨迹方向和水下复杂噪声有关。上述因素会导致定位误差在较小范围内波动，进而产生上述的现象。但是，从水平位置误差来看，整体上本文方法的定位精度优于其他两种方法。

基于SINS/DVL 的组合导航系统考虑到IMU 和DVL 均有测量误差，因此，系统的定位误差会随着时间不断累积。图11 的水平定位误差出现了较大波动，导致首段和尾端出现了较高精度。同时，这种情况和载体的运动轨迹有关。当水平位置误差发散方向与载体运动方向相同时，会存在误差减少的情况。但是，这种现象只是局部的，从长期导航过程来看，定位误差仍然越来越大。

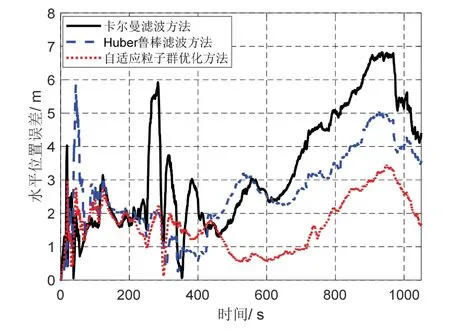
图11 湖试水平位置误差Fig.11 Horizontal position error for lake test

表4 给出三种方法的水平位置误差均值和最大值。从表中可以看出：三种方法的水平位置误差均值分别为3.30 m、2.65 m 和1.67 m，相比于其他两种方法，本文方法的水平位置误差均值分别减少了49.39%和36.98%；三种方法的水平位置误差最大值分别为6.82 m、5.85 m和3.44 m，相比于其他两种方法，本文方法的水平位置误差最大值分别减少了49.56%和41.20%。

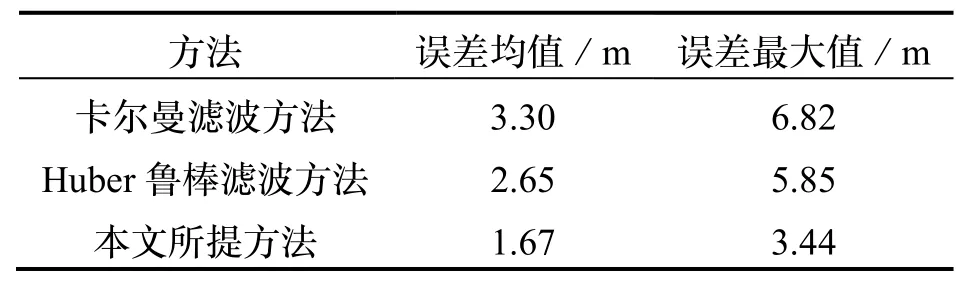
表4 三种方法的水平位置误差均值和最大值Tab.4 Mean and maximum horizontal position error for three methods

4 结论

本文针对复杂环境下SINS/DVL 自主导航系统易受干扰的问题，提出了一种自适应粒子群优化的SINS/DVL 组合导航方法。本文从模型和算法两个方面进行分析：在模型方面，针对系统矩阵计算容易产生方差估计不一致问题，基于状态变换原理，用重力矢量替代不稳定的比力向量，推导了相关导航模型；在算法方面，在Huber 鲁棒滤波算法的基础上，引入并改进了粒子群优化算法，实现了系统噪声方差阵和量测噪声方差阵的自适应估计。最后在实验验证方面，分别设计了仿真实验并搭建了湖试实验。实验结果表明，本文方法在复杂干扰环境下其定位性能优于卡尔曼滤波方法和Huber 鲁棒滤波方法，定位精度得到进一步提升。