基于模糊层次分析法的在役高桩码头安全性评估

李 琳，孙克俐

（天津大学建工学院港口工程系，天津 300350）

引言

作为领土东部临海的沿海国家，我国丰富的海岸线资源为港口码头建设提供了良好的条件。截止到2019 年底，我国沿海共拥有6 426 个泊位，其中万吨级泊位2 076 个[1]，高桩码头结构应用最广泛，如何对在役的高桩码头结构进行准确科学的安全性评估，国内外学者尚未给出统一的方法，一般采用模糊评价法和灰色理论等方法，本文充分考虑影响码头结构安全的因素，运用模糊层次分析法对高桩码头进行安全性评估。

1 模糊层次分析法理论

层次分析法即AHP 理论，于上世纪70 年代由美国学者Saaty 提出，该方法将目标分解为多个目标和准则，将定性问题定量化，其基本步骤如下：

1）建立层次结构模型。这一步骤主要通过分析具体问题，建立目标层、准则层、指标层；

2）构造两两判断矩阵。这一步骤主要对从属于上一层次的本层元素进行比较，建立判断矩阵；

3）进行一致性检验，计算权重。这一步骤主要通过计算判断矩阵的最大特征根及对应的特征向量，利用一致性指标检验判断矩阵是否合理，若合理，则对应的特征向量即为权向量，若不合理，则需要重新构造判断矩阵。

模糊综合评判法是综合利用模糊数学的基本方法，考虑对被评价对象有影响的各个因素对其做出综合评价，其基本模型大致如下：

1）确定评判对象的元素集U=(U1,U2,…,Un)；

2）确定评语集X=(X1,X2,…,Xm)；

3）单因素评判，即建立从U到X的模糊映射，然后求出模糊关系R，R即为单因素评判矩阵，它由所有对单因素评判的模糊集组成。

模糊层次分析法是将层次分析法与模糊综合评判法相结合，用层次分析法确定各指标的权重，再用模糊综合评估方法对各指标进行模糊评价的方法，其基本步骤如下：

1）建立层次结构模型；

2）构件判断矩阵，确定各因素权重；

3）建立评语集与评估因素集；

4）针对具体工程实际应用。

在确定权重的过程中，构造合适的判断矩阵是关键一步，本文将传统的需要进行一致性检验构造判断矩阵的方法与范春彦[2]提出的改进方法进行比较，为评估在役高桩码头的安全性提出建议。

2 建立层次结构模型

高桩码头结构主要由上部结构、桩基、接岸结构、码头设备等设施组成，《水运工程水工建筑物检测与评估技术规范》（JTS 304-2019）对在役水工建筑物的安全性、适用性和耐久性均提出了评估分级要求[3]，本文按照构件型式将高桩码头结构划分为梁、板、桩、桩帽、靠船构件和接岸结构六大部分，主要从外观质量、构件裂缝、钢筋锈蚀、承载能力、沉降、位移等方面对各构件进行评估，从而确定在役高桩码头结构的安全性。

3 评估指标的权重确定

确定指标权重主要是通过两两比较方法构造相应的判断矩阵，本文对比两种确定权重的方法，给出合理建议。传统的层次分析法采用1-9 标度法（表1），通过对所构造的判断矩阵进行一致性检验确定对应的权向量即为指标权重。改进的层次分析法也采用1-9 标度法，根据专家给出的任一行判断结果，得出各个指标所占权重的信息，据此信息得到各指标的对应权重。

表1 九标度判断尺度表

3.1 传统层次分析法确定权重

采用传统的层次分析法确定权重时，一般采用1-9 标度法[4]（见表1）构造对应的判断矩阵，通过相对性一致指标C.R.检验其一致性其中为判断矩阵的最大特征值，n为所构建判断矩阵的阶数，R.I.为平均随机一致性指标[4]（见表2），与矩阵阶数有关。一般认为当C.R.＜0.1时，判断矩阵的一致性是可以接受的。通过两两比较梁、板、桩、桩帽、靠船构件、接岸结构对结构安全的影响程度，邀请专家运用上述方法并结合在役高桩码头结构安全性评估指标体系对各构件进行重要性判断，比较结果如表3 所示。

表2 平均随机一致性指标

表3 比较结果

其对应的判断矩阵为：

使用Matlab 软件计算得到该矩阵最大特征值为λmax=6.1225，验证判断矩阵的一致性得到：

由于C.R.=0.0194 ＜0.1,则该判断矩阵的一致性符合要求，计算得到最大特征值对应的特征向量为(0.2504,0.1596,0.3825,0.1006,0.0641,0.0428)，则梁、板、桩、桩帽、靠船构件、接岸结构所对应的权重为：

W=(0.2504,0.1596,0.3825,0.1006,0.0641,0.0428)

用相同的方法计算指标层的权重，计算结果如表4 所示。

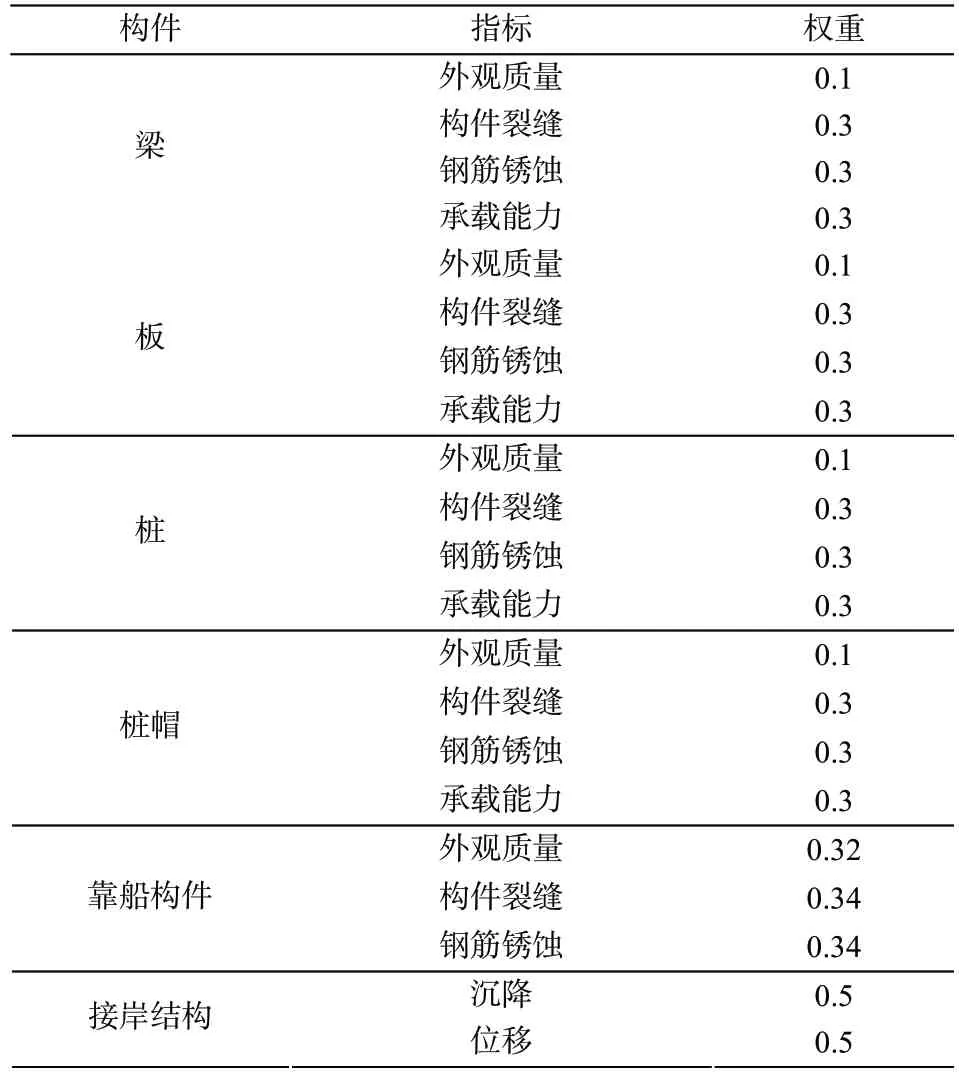
表4 指标层权重

3.2 改进的层次分析法确定权重

根据上述方法计算梁、板、桩、桩帽、靠船构件和接岸结构的权重信息。首先计算判断矩阵，再以判断矩阵每一行为基础构造新的矩阵。其中专家判断矩阵为：

以矩阵A 的每一行元素为基础，构造新的一致性矩阵并计算对应的特征向量，以第一行为例构造新矩阵计算其特征向量：

同理可计算以其余行为基础的特征向量：

其对应的特征向量为：

用相同方法确定准则层的权重发现与传统层次分析法确定的权重相同，如表4 所示。

4 建立评语集与评估因素集

4.1 建立评语集

根据《水运工程水工建筑物检测与评估技术规范》（JTS 304-2019）将高桩码头安全性分为4 个等级，其相应的评语集为（A，B，C，D），对应的码头结构安全状态为（完好，良好，差，危险），具体评估标准如表5 所示[3]。

表5 水运工程水工建筑物安全性评估分级标准

隶属函数最早是由美国学者泽德在1965 提出，作为模糊数学最显著，最重要的特征，它描述了事物存在的不确定性，是用来表征模糊集合的数学工具，本文选取更能反应高桩码头安全性。

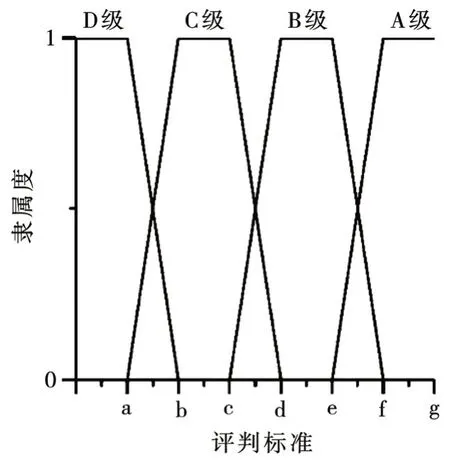
图2 梯形分布隶属函数图像

4.2 建立评估因素集

根据在役高桩码头结构安全性评估指标体系可知，在役高桩码头结构的安全性评估属于二级模糊综合评判，其一级因素集为：在役高桩码头安全性=（梁，板，桩，桩帽，靠船构件，接岸结构）；在役高桩码头结构安全性模糊评估的二级因素集为：

U1=（u11,u12,u13,u14），即：梁安全性=（外观质量，构件裂缝，钢筋锈蚀，承载能力）；

U2=（u21,u22,u23,u24），即：板安全性=（外观质量，构件裂缝，钢筋锈蚀，承载能力）；

U3=（u31,u32,u33,u34），即：桩安全性=（外观质量，构件裂缝，钢筋锈蚀，承载能力）；

U4=（u41,u42,u43,u44），即：桩帽安全性=（外观质量，构件裂缝，钢筋锈蚀，承载能力）；

U5=（u51,u52,u53），即：靠船构件安全性=（外观质量，构件裂缝，钢筋锈蚀）；U6=（u61,u62），即：接岸结构安全性=（沉降，位移）。

对在役高桩码头进行二级综合模糊评判根据下式进行计算：

其中，R为评判矩阵，W为权重矩阵，◦为模糊合成算子，本文采用Zadeh 算子(∧,∨)计算[5]，外观质量，构件裂缝，钢筋锈蚀，承载能力，沉降，位移的评级根据《水运工程水工建筑物检测与评估技术规范》（JTS 304-2019）中的相关规定进行评判，其隶属度函数采用梯形分布（图1），采用最大隶属度原则确定各构件及码头结构安全等级。

5 工程实例

浙江舟山某高桩梁板式码头长208.2 m，宽18.0 m，上部结构由纵横梁和预制迭合面板组成，基础为600 mm×600 mm 钢筋混凝土方桩，根据现场资料，结合相关规范，根据模糊数学的方法确定评价集的隶属度参数如表6 所示。

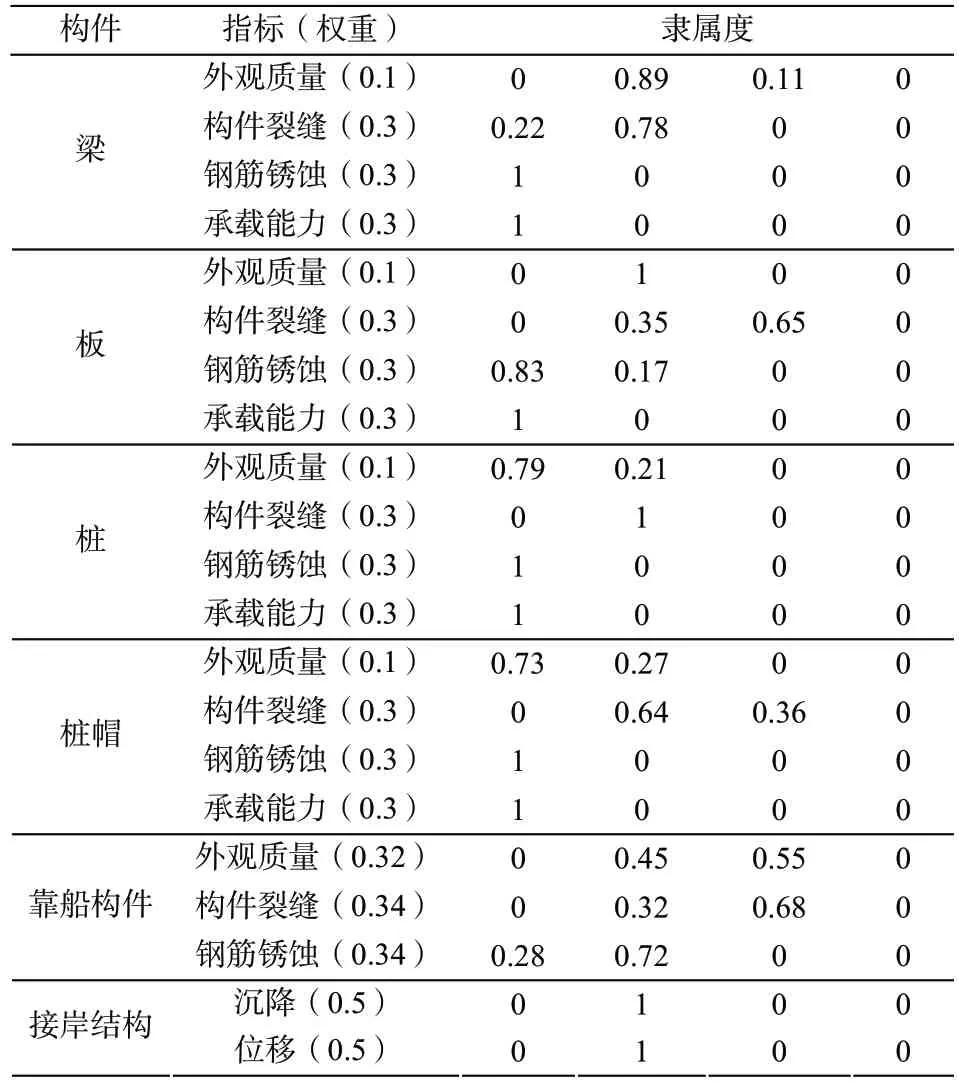
表6 评估指标隶属度

对该码头进行模糊综合评判，则对梁的安全性模糊综合评判如下：

归一化得：V11=（0.43,0.43,0.14,0），同理得在役高桩码头结构板、桩、桩帽、靠船构件和接岸结构的安全性模糊综合评判结果为：

使用传统层次分析法确定的码头各构件权重为：W=（0.2504,0.1596,0.3825,0.1006,0.0641,0.0428）则此时在役高桩码头安全性模糊综合评判结果为：

根据最大隶属度原则，该高桩码头结构属于完好状态为41 %，属于良好状态为41 %，属于差的状态为18 %。

据2.2 节知使用传统层次分析法和改进层次分析法确定的影响各构件安全性的各指标权重相同，则得到的模糊判断矩阵R相同，据2.3 节使用改进层次分析法确定的高桩码头各构件权重为W=(0.2374,0.1740,0.3564,0.1286,0.0626,0.0410)，则此时在役高桩码头安全性模糊综合评判结果为：

根据最大隶属度原则，该高桩码头结构属于完好状态为40 %，属于良好状态为40 %，属于差的状态为20 %。

6 结语

本文从影响高桩码头各构件安全性的因素出发，建立了在役高桩码头结构安全性评估指标体系。运用传统层次分析法与改进的层次分析法确定各指标权重，结果表明两种方法都具有较高的准确性。若专家把握较大可采用传统层次分析法计算指标权重，若专家对判断把握不大，则可以采用改进的层次分析法确定各指标权重。针对对具体工程实例，将层次分析法与模糊综合评判法相结合，将在役高桩码头安全性评估层次化，定量化，验证了模糊层次分析法在结构安全评估方面应用的可靠性和准确性，具有较高的实用价值。