高等数学视角下的弧微分公式推导及曲率公式适用条件

强 静, 邵 虎, 张双圣

(1.中国矿业大学 数学学院, 江苏 徐州 221116; 2.徐州工程学院 环境工程学院, 江苏 徐州 221018)

0 引 言

国内大多数《高等数学》(《微积分》)教材[1-3]在曲率一节中,首先引入弧微分,然后才给出曲率的定义,最后运用弧微分公式推导曲率公式.开篇引入弧微分,略显突兀,而且在证明弧微分公式时直接使用了“弧长和弦长的比值极限为1”这个假设,证明过程不严谨,学生对此常常感到疑惑.

目前,一些研究《高等数学》的学者试图运用微分理论证明弧微分公式,提出了一些有趣的方法[4-5],但这些方法有不足之处.比如,文献[4]构造了一个不等式,运用夹逼准则证明弧微分公式,虽然弦长确实小于弧长,但是弧长未必小于文献[4]中所给两条线段的和,证明过程出现了疏漏;文献[5]运用单调有界数列必有极限定理,仅证明了光滑曲线弧在一种分割方式下内接折线长度的极限存在,就认为光滑曲线弧是可求长的,据此又证明了弧微分公式,这种证明过程显然也有漏洞.另外,《数学分析》[6]中运用积分理论,证明了光滑曲线弧(曲线方程为参数方程)是可求长的,从而得到了弧微分公式,但该证明方法比较繁琐,其中涉及到一致连续的性质的使用,对于非数学专业学生来说难度较大,不易理解.

为了解决上述问题,本文首先引出曲率的定义,并给出一种新的曲率的定义形式;在高等数学知识体系内给出一种严谨证明弧微分公式的方法;针对上述四种不同形式的曲线方程,推导并总结了四种不同方程下的曲率公式及适用条件;给出二个典型例题说明四种曲率公式的情景应用;最后,给出了一个运用曲率公式求解实际工程问题的案例.以期为研究平面曲线的曲率问题提供借鉴,也为《高等数学》教材改革中曲率部分的编写提供参考.

1 曲率的定义

在生产实践和工程技术中,研究曲线的弯曲程度是经常遇到的一类问题,比如火车轨道缓和曲线设计问题,火车通过弯曲轨道时向心力大小的影响问题以及大桥在荷载作用下产生弯曲变形问题等.因此如何定量描述曲线的弯曲程度具有重要的现实和理论意义.曲率就是描述曲线的弯曲程度的量.

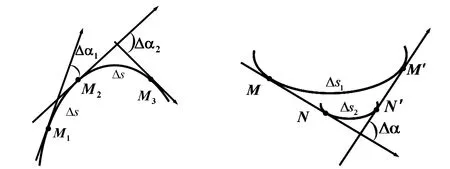
图1 弧长相同条件下的曲线 图2 转角相同条件下的曲线

图3 一般情况下的曲线C

2 弧微分公式推导

图4 曲线y=f(x)上弧及其内接折线

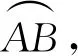
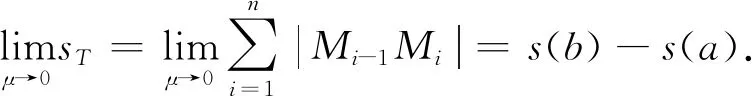
定理1假设曲线y=f(x)在区间[a,b]上可导且导函数f′(x)连续,则曲线是可求长的,且

证由微分中值定理得

Δyi=f(xi)-f(xi-1)=f′(ξi)Δxi,ξi∈[xi-1,xi].

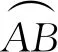
又因为

当μ→0时,对于∀i(1≤i≤n),均有

根据极限运算的换元法则得

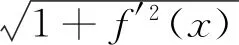
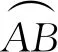
3 曲率公式推导

曲线方程(i):y=f(x),且f(x)具有二阶导数.

在图3中,因为tanα=y′,所以

(1)

曲率公式(1)的适用条件是y=f(x)二阶可导.

曲线方程(ii):x=h(y),且h(y)具有二阶导数.

在图3中,因为tanβ=x′,所以

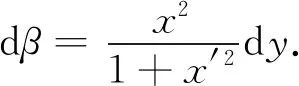
(2)

曲率公式(2)的适用条件是x=h(y)二阶可导.

由于φ′2(t)+ψ′2(t)≠0,不妨设φ′(t)≠0,根据参数方程求导公式可得

代入公式(1)得到曲率公式如下:

(3)

如果φ′(t)=0,则ψ′(t)≠0,根据参数方程求导公式可得

代入公式(2)可得曲率公式:

与公式(3)相同.

曲率公式(3)的适用条件是x=φ(t)及y=ψ(t)均二阶可导,且φ′2(t)+ψ′2(t)≠0.

曲线方程(iv):由极坐标方程ρ=ρ(θ)给出,ρ(θ)二阶可导,且ρ2(θ)+ρ′2(θ)≠0.

x′(θ)=ρ′(θ)cosθ-ρ(θ)sinθ,x″(θ)=ρ″(θ)cosθ-2ρ′(θ)sinθ-ρ(θ)cosθ,

y′(θ)=ρ′(θ)sinθ+ρ(θ)cosθ,y″(θ)=ρ″(θ)sinθ+2ρ′(θ)cosθ-ρ(θ)sinθ.

将上述4式代入到曲率公式(3)可得极坐标系下曲率公式,如下:

(4)

曲率公式(4)的适用条件是ρ=ρ(θ)二阶可导,且ρ2(θ)+ρ′2(θ)≠0.

4 例 题

为了进一步说明各曲率公式的适用条件,给出两个典型例题.其中,例1用来说明曲率公式(1)-(3)适用条件,例2用来说明曲率公式(4)的适用条件.

例1求椭圆4x2+y2=4在点(1,0)及点(0,2)处的曲率.

解① 点(1,0)处的曲率

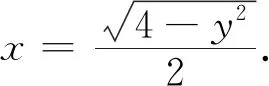
x′(t)=-sint,x″(t)=-cost,y′(t)=2cost,y″(t)=-2sint.

② 点(0,2)处的曲率

根据公式(1)可知点(0,2)处的曲率K=2.

满足曲率公式(3)适用条件,根据公式(3)可得点(0,2)处曲率K=2.

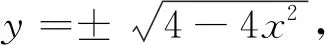
例2试求阿基米德螺线ρ=aθ(a>0)上任一点处曲率,并讨论哪一点处曲率最大.

5 实际应用

这虽然是一个经典实际问题,在文献[6,14]中都有阐述,但是文献[6]中没有详细解答过程,文献[14]中缓和曲线推导过程比较复杂.本文给出一种更合理的方法设计缓和曲线.

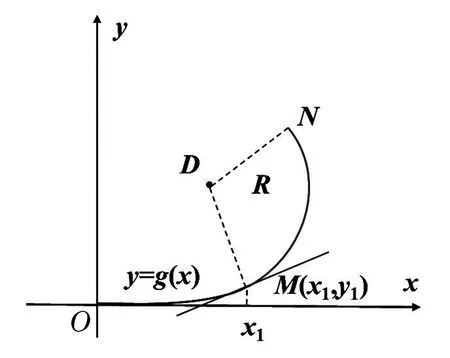
图5 铁轨缓和曲线示意图

g(0)=0,g′(0)=0,g″(0)=0,

(5)

6 结 论

在高等数学知识体系内,利用曲线直角坐标方程得到了弧长与有向弧段的值之间的关系,证明了弧微分公式.证明过程中不需要使用一致连续的性质,相对简洁,且避免了弧微分公式推导过程中“弧长和弦长的比值极限为1”这个假设,使弧微分公式及曲率公式的推导过程更加严谨.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.