定积分的一个渐近展开

韩淑霞, 韩志斌, 黄永忠

(华中科技大学 数学与统计学院,武汉 430074)

0 引 言

熟知,若函数f(x)在闭区间[a,b]上可导,且导函数f′(x)在[a,b]上可积,则成立[1]

特别地,若区间[a,b]是[0,1],则

(1)

这是定积分中一个有用的结论,用该结论容易得到2014年第六届全国大学生数学竞赛预赛(非数学类)第六题,以及2017年第九届预赛(数学类)第五题的解答. 在减弱条件的情况下,文献[2]对该结论的否命题形式给出反例,文献[3]在单侧导数条件下推广了相关的结论.

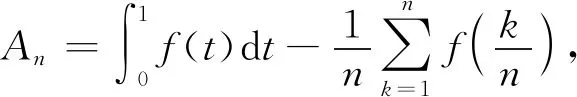
(上式中的f′(0)应为f′+(0).为简便计,区间端点处的单侧导数还是用导数表示,高阶时也如此.)

也就是说,若函数f(x)∈C2[0,1],则当n→∞时,

于是,可以猜测,若f(x)∈Cm[0,1](m为正整数),则当n→∞时有

(2)

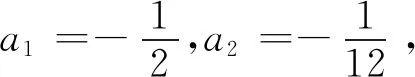
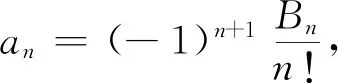
文献[1]习题4.1.8是Riemann和中的介点取分割小区间的中点,成立

类似地,本文得到f(x)∈Cm[0,1]条件下的式子(见命题2):

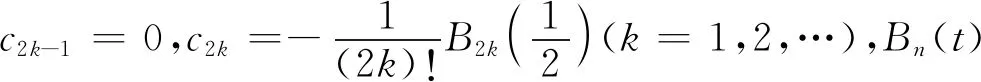
1 预备知识

积分型余项的Taylor公式[4]设函数f在区间 (a,b)上有n+1阶的连续导数,则对任意的x,x0∈(a,b) 都成立

(3)

Bernoulli数Bn和Bernoulli多项式Bn(t) 满足下列两个等式[5-6]

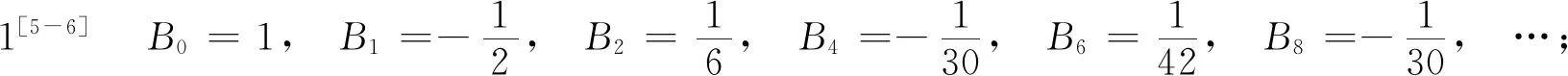
(4)

Cauchy乘积[7]

(5)

2 主要命题

命题1若函数f(x)∈Cm[0,1](m为正整数),则当n→∞时,成立

(6)

其中系数ai(i=1,2,…,m)满足

(7)

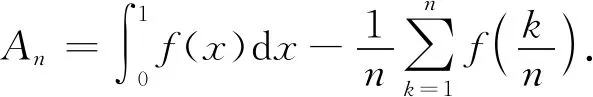
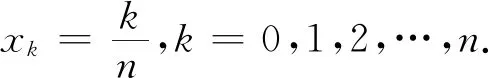
因为对j∈{1,2,…,m-1},有

且存在ξk∈[xk-1,xk] ,用二次积分换序得

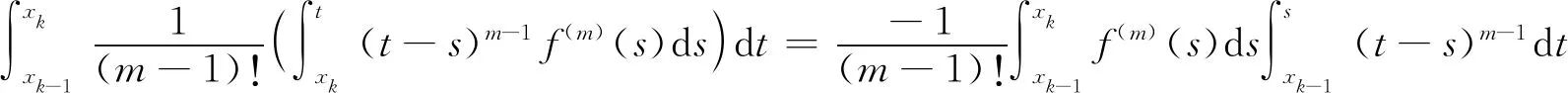
所以

于是

故

对j∈{1,2,…,m},有

由积分型余项的Taylor公式(3),有

从而存在ηj,k∈[xk-1,xk]使得

因此,对j∈{1,2,…,m-2}得到

又,对j=m-1有

故

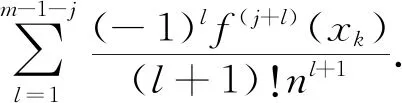
因为

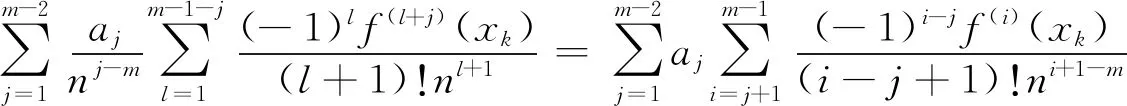
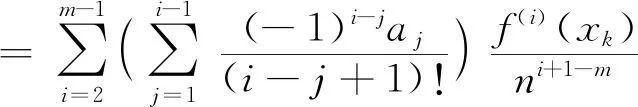
所以

注意到

得到

于是,若系数ai满足

则

下面利用Bernoulli数Bi刻画系数ai,得到有趣的结论. 对此,将式(7)统一为

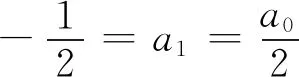
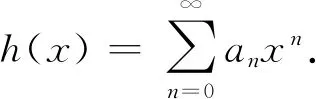
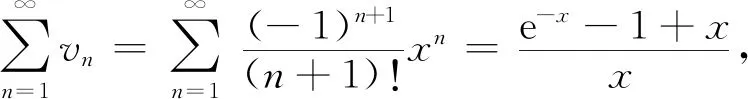
h(x)(e-x-1+x)=x(h(x)-a0)=x(h(x)+1),

解得

由幂级数展开式的唯一性,命题1中的系数可以用Bernoulli 数表示为

(8)

由此,重写命题1为

命题1′若函数f(x)∈Cm[0,1](m为正整数),则当n→∞时,成立

(9)

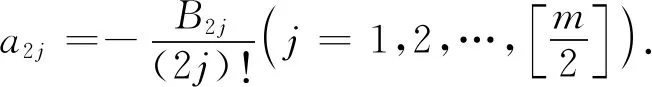
注2 根据注1的式(4)以及式(8),命题1’式(9)的系数满足

注3 若将区间[0,1]改为[a,b],令x=a+t(b-a),则命题1’的式(10)为

命题2若函数f(x)∈Cm[0,1](m为正整数),则当n→∞时,成立

(10)

其中,若m<4则无求和的∑项,系数cn满足

(11)

证分别处理式(10)的项Tn和Ω,其中

计算得到

(12)

其中ξk,1∈[xk-1,yk],ξk,2∈[yk,xk].于是由积分型余项的Taylor公式(3),有

其中,当j为偶数时,δj=1;当j为奇数时,δj=0.

另一方面,计算

由积分型余项的Taylor公式(3),有

由式(12),以及

其中ηj,k1∈[xk-1,yk],ηj,k2∈[yk,xk],得到

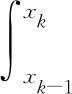
因此,对j∈{1,2,…,m-2}得到

又,对j=m-1,存在ζm-1,k1∈[xk-1,yk],ζm-1,k2∈[yk,xk]使得

故

于是,注意到

得到

因此,若系数cj满足

(13)

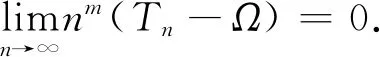
为进一步分析系数cj,重写式(13)为

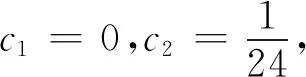
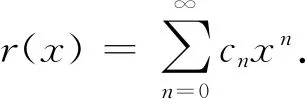
即

解得

由幂级数展开式的唯一性,得到

即式(11)成立.

3 结 论

对于具有m阶连续可微的被积函数,给出了其定积分的渐近展开式(类似于Taylor公式形式). 命题1中给出了介点取右端点的渐近展开式,命题2中给出了介点取两分点中间值的渐近展开式.

致谢作者非常感谢参考文献对本文的启发以及审稿专家提出的宝贵意见.