一种高效的联邦学习隐私保护方案

宋 成,程道晨,彭维平

(河南理工大学 计算机科学与技术学院,河南 焦作 454003)

1 引 言

随着处理器性能的不断提升,机器学习在自动驾驶、虚拟现实、医疗诊断等众多智能应用中发挥着重要作用。然而,传统的机器学习方法将数据集中在一台机器或中央服务器上,无法为用户的个人隐私提供足够的保护。虽然通过收集大量的用户数据进行训练能够提升机器学习的性能,但是收集数据的同时不可避免的会导致用户信息的隐私泄露,如患者病历、行人轨迹、和社交网络等。随着公众隐私保护意识的增强,越来越多的用户不愿意向企业提供个人信息。因此,在充分发挥机器学习的潜力基础上,如何确保用户个人的数据隐私是一项意义深远而又亟待解决的问题。为了解决这一问题,谷歌提出了联邦学习(Federated Learning,FL)[1]的思想,即多个参与方在不共享原始数据的情况下协作训练模型,进而避免个人数据隐私泄露,并有效解决数据孤岛问题。

尽管联邦学习避免将数据直接暴露给第三方,对于数据起着一定保护作用,但是联邦学习场景下依然存在隐私泄露风险[2]。不可信服务器有权获取每个参与者局部训练模型的大量辅助知识[3](如模型结构、初始化参数等),WANG等[4]利用对抗生成网络(Generative Adversarial Networks,GAN)通过在服务器部署多任务生成对抗网络mGAN-AI,对数据的真伪、类别和归属用户进行判别,利用更新值重构参与者的典型数据。ZHU等[5]发现恶意攻击者根据部分更新的梯度信息能够窃取原始训练数据。因此,采用基于差分隐私(Differential Privacy,DP)[6]、安全多方计算(Secure Multi-party Computation,SMC)[7]和同态加密(Homomorphic Encryption,HE)[8]等技术保护梯度机密性的相关方案被提出。

差分隐私通过在本地模型训练过程中对相关参数添加扰动,从而令攻击者无法从用户发布的信息中推导出用户的隐私。但差分隐私添加的噪声影响模型的精度,如何平衡模型精确度与保护隐私度是巨大的挑战[9]。安全多方计算使联邦学习可以在无可信第三方的情况下,互不信任的各方在不泄露其原始数据的情况下安全合作。但参与者之间需要进行多轮交互才能实现安全聚合,且不支持用户退出,对于资源受限参与者无法承担巨大的计算及通信压力。同态加密在为数据的传输提供强有力的隐私保护的同时,还可确保模型与集中训练的准确性一致。PHONG等[10]提出一种基于加法同态加密机制的联邦学习隐私保护方案PPDL,方案由任意一个终端生成密钥对并分享给其他终端,终端用公钥对本地的梯度加密上传,中心服务器对密文加法同态计算后下发,终端利用私钥解密获得更新的全局梯度。该方案是联邦学习通用的同态加密方案[11],适用于Paillier等多种非对称同态加密机制。

联邦学习在分布式参与者交互过程中,每个参与者需在本地周期上传完整的梯度更新。由于机器学习通常基于复杂的深度神经网络,梯度更新可能产生巨量参数,使得联邦学习通信开销大幅提高。尤其在隐私保护相关的实际应用中,资源受限的设备难以承受加密运算带来的额外计算开销[12]。为了解决同态加密运算所带来的通信效率问题,ZHANG等[13]利用中国剩余定理(Chinese Remainder Theorem,CRT)首先对模型梯度进行压缩,然后采用Paillier同态加密算法加密后上传服务器;尽管方案通信效率有所提升,但压缩操作会为参与者带来额外的计算开销,且模型收敛速度下降。ASAD等[14]为了实现通信成本最小化,将CMFL[15]中的梯度选择机制和基于非交互式零知识证明的同态加密系统相结合,提出一种通信高效的同态加密联邦学习方案CEEP-FL;尽管方案通信次数明显减少,但选定的客户端仍会上传完整的模型更新参数,通信量并未降低。

综上所述,当前在联邦学习环境中应用隐私保护方法存在以下几个问题:

(1) 联邦学习中应用差分隐私等方法的模型准确率容易受到影响。

(2) 简单地将隐私保护技术,例如安全多方计算、同态加密等,应用到联邦学习中可能产生大量额外的通信开销。

(3) 资源受限的本地设备使得联邦学习的隐私保护方法有待于进一步降低计算成本。

针对以上问题,笔者提出了一种基于同态加密的高效安全联邦学习隐私保护方案,通过优化Paillier同态加密方案,将大指数模运算和指数乘法运算化为简单的基本操作,减少加密阶段的运算时间。同时设计一种梯度过滤压缩算法,过滤掉收敛趋势不相关的本地更新,并采用计算可忽略的压缩操作符量化更新参数以减少通信开销。主要贡献如下:

(1) 通过优化Paillier同态加密算法,在不降低安全性的前提下将加密阶段的大指数模乘法运算简化为基本运算,提高算法效率,进而提高资源受限环境下联邦学习隐私保护方案的性能。

(2) 通过将梯度选择与自然压缩算子相结合,设计一种梯度过滤压缩算法,过滤掉收敛趋势不相关的本地更新,并采用计算可忽略的压缩操作符量化更新参数以减少通信开销,在减少通信次数的同时降低通信开销。

(3) 对方案的正确性及安全性提供了形式化的证明和分析,在常用数据集上进行的图像分类实验结果表明,与近期最新的相关算法[14]和同态加密基线算法[10]相比,文中的算法实现了通信效率、隐私保护及模型准确率三者的有效平衡。

2 预备知识

2.1 联邦学习

联邦学习的思想是首先通过中央服务器将用于训练本地数据集的全局模型发送到分布式客户端,客户端利用本地数据对模型进行训练,然后将训练后的模型参数返回到中央服务器;中央服务器接收到来自分布式客户端的本地训练的模型参数后更新全局模型参数,再将更新的全局模型参数发送到客户端。重复以上训练过程,直到模型完成收敛。

联邦学习通过将训练阶段分布到多个参与者中,从而实现去中心化的机器学习服务。本地化的模型训练避免了用户将自己的数据暴露给企业或者其他参与方,使联邦学习在客户端数据隐私保护方面具有明显优势。联邦学习架构如图1所示,在一次完整的训练过程中,中心服务器首先将初始全局模型传输给多个客户端;客户端收到全局模型后,使用本地训练数据集来训练局部模型;然后客户端将他们的本地更新参数上传到中央服务器;最后中央服务器进一步聚合和平均,以获得新的全局模型。

图1 联邦学习架构

2.2 Paillier同态加密

文中通过优化Paillier同态加密,在确保整个联邦学习过程的机密性和安全聚合的基础上,减少运算量,提高算法效率。Paillier密码系统描述如下。

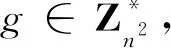
ENC:对任意明文m∈Zn,随机生成一个数字r,满足gcd(r,n)=1,计算密文c=gm·rnmodn2。

DEC:给定聚合密文c对应的聚合明文为m=μ·L(cλmodn2)modn。

2.3 自然压缩

自然压缩[16]是一个基于随机对数舍入的函数Cnat:RR,Cnat(0)=0。当x≠0时,假设α满足2≤|x|=2α≤2,则

(1)

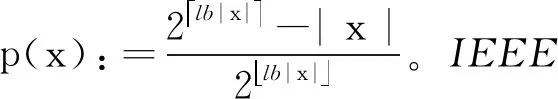
3 方案概述

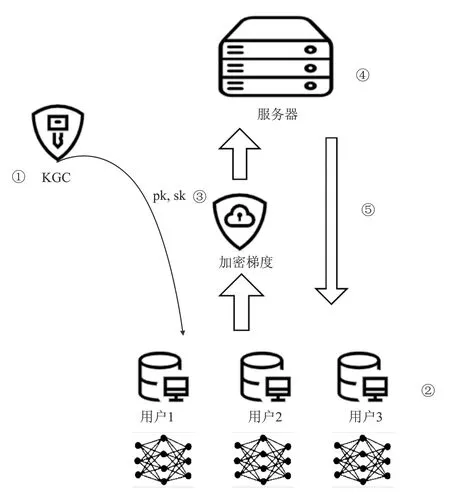
图2 文中方案系统模型

3.1 系统模型

方案包括初始化、模型训练、加密、聚合、全局模型更新5个阶段,由密钥生成中心(Key Generation Center,KGC)、服务器和客户端3个实体组成,如图2所示。实体功能如下。

密钥生成中心:独立可信的机构,负责分发和管理所有的公钥和私钥。

服务器:负责接收用户提交的所有梯度,并对其进行聚合,从而获得优化的全局模型。

客户端:在服务器的协调下协作训练统一的模型。每个客户端首先在设备上的私有数据上训练本地模型,然后将加密的梯度上传到服务器。

3.2 威胁模型

文中方案的安全模型假设中心服务器是不受信任(诚实且好奇)的对手,而所有的参与者都被视为受信任的实体。诚实且好奇的服务器意味着它将忠实地遵循设计的联邦学习协议,但试图从每个用户的本地更新推断私人信息。由于不受信任的服务器可推断出每个参与者的本地梯度中的敏感信息,因此针对不受信任的服务器需提供强大的隐私保障。

4 方案设计

4.1 Paillier同态加密算法优化

gm=(1+n)∂mβmnmodn2=(1+∂mn)modn2。

(2)

显然,计算量大的大指数幂模运算可转化为计算量小的多项式模运算。根据式(2)和卡迈克尔定理,Paillier加密的密文c=(1+n)∂mβmnrnmodn2=(1+∂mn)rnmodn2可改写为

c=(1+n)∂mβmnrnmodn2=(1+∂mn)rnmodn2,

(3)

其中,rnmodn2可以在密钥分配阶段提前计算。同理可得,μ=L(gλmodn2))-1modn=L(1+∂λnmodn2)-1modn=(∂λ)-1modn。由于加密阶段的∂可在解密阶段消去,因此Paillier同态加密算法可优化如下。

ENC:对任意明文m∈Zn,随机选择一个v,计算c=(1+mn)·v。

DEC:给定聚合的密文c,对应的聚合明文为m=L(cλmodn2)bmodn。

4.2 梯度过滤压缩算法设计

本节设计一种梯度过滤压缩算法,首先计算全局更新与局部更新参数的相关性。梯度相关性公式为

(4)

相关性越高,局部更新就越遵循全局优化方向;相关性越低,局部更新就越不会对全局优化造成影响。通过设置阈值,阻止客户端上传不相关的本地更新,减少不必要的通信开销,同时降低对模型准确性的影响。为了进一步降低通信成本,使用自然压缩算子对过滤后的梯度执行压缩。 梯度过滤压缩算法实现如下:

梯度过滤压缩算法

输入:客户端索引i,更新梯度gt+1,原始梯度gt,相关性阈值H

① 根据式(4)计算e(gt+1,gt)

② ife(gt+1,gt)≤H

③ return null

④ else

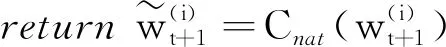
文献[16]证明自然压缩算子Cnat的方差只有1/8,因此几乎不会影响模型收敛速度。梯度过滤压缩算法仅选择强相关的梯度更新,提高了模型收敛速度,每次梯度更新再通过自然压缩算子量化,从而减少了通信开销。

4.3 基于同态加密的隐私保护方案

4.3.1 系统初始化阶段

步骤1 KGC负责分发和管理所有的公钥和私钥(pk,sk)。KGC通过运行优化后的Paillier同态加密的KeyGen算法,生成公钥/私钥对(pk,sk)={(n),(λ,b)}。

步骤2 KGC广播公钥pk,并将私钥sk和系统参数v通过安全通道发布给客户端。

步骤3 服务器将系统参数params={B,E,H,η,w}发布给客户端。

4.3.2 模型训练阶段

客户端i基于本地数据集,通过运行随机梯度下降(Stochastic Gradient Descent,SGD)算法训练本地模型,并运行梯度过滤压缩算法。具体步骤如下:

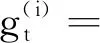
步骤2 客户端i执行梯度过滤压缩算法,计算下一轮通信局部模型更新相关性e(gt+1,gt),如果e(gt+1,gt)≤H,返回步骤1;否则,执行步骤3。

4.3.3 加密阶段

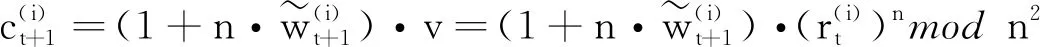
4.3.4 聚合阶段

设mt+1为第t+1轮通信的抽样参与者总数。服务器收到mt+1加密更新后,首先计算聚合结果:

4.3.5 全局模型更新阶段

5 方案分析

5.1 正确性分析

定理1优化后的Paillier密码算法满足解密正确性。

证明:将加密公式代入,可得

Dec(c)=L(cλmodn2)bmodn=
L(((1+mn)rnmodn2)λmodn2)bmodn=
L((1+mn)λrλnmodn2)bmodn。

根据卡迈克尔定理[18]有rλn=1 modn2,可得Dec(c)=L((1+mn)λmodn2)bmodn,高阶多项式按二项式定理展开并代入L(u),b,得Dec(c)=L((1+λmn) modn2)bmodn=(λm)λ-1modn=m。因此,优化后的Paillier密码算法满足解密正确性。

定理2改进的Paillier密码系统满足加法同态性。

那么,Enc(x)⊗Enc(y)=Enc(x+y)成立。解密过程可以通过相同的方法获得,即Dec(Enc(x)⊗Enc(y))=x+y。

5.2 安全性分析

5.2.1 不可区分性

选择明文攻击(Chosen Plaintext Attack,CPA):对于Paillier同态加密方案,考虑挑战者C与攻击者A之间的如下博弈。

初始阶段:首先挑战者C运行系统初始化获取系统公共参数,并运行秘钥生成算法生成公私钥对(pk,sk);然后将系统公共参数和公钥发送给攻击者A。

挑战阶段:首先攻击者A选择两个长度相同的明文m0,m1,并将它们提交给挑战者C;然后挑战者C随机选取b∈{0,1},计算C*=ENC(pk,mb),将密文C*发送给攻击者A。b对攻击者A保密,攻击者A输出b′∈{0,1}作为对b的猜测;如果b′=b,则攻击者A赢得该博弈。

定理3如果攻击者A在多项式时间内以可忽略的概率赢得该博弈,即优势

(5)

则在λ中可以忽略。方案满足选择明文攻击下的不可区分性。

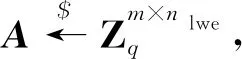
(6)

5.2.2 数据隐私性

恶意攻击者可通过窃取用户之间交换的数据分析推断用户的隐私信息。由于Paillier算法能够实现用户的隐私保护,因此,需证明优化后的Paillier算法与原Paillier算法安全性等价。

定理4优化后的Paillier密码算法与原Paillier算法的语义安全性是等价的。

证明:对任意明文m∈Zn,根据二项式定理得到优化后的密文c1=(1+n)mrnmodn2=(1+mn)rn·modn2,原Paillier算法的密文为c2=gmrnmodn2。由2.1节可知,g可分解为1+n,由于二者均为判断模n2的剩余问题,因此,将上面两密文恢复明文具有相同的难度,即优化后的Paillier算法和原本的Paillier算法具有相同的安全性。

5.2.3 模型安全性

6 实验结果

实验环境为:Ubuntu18.04系统,Intel(R)Core(TM) i7-7700HQ CPU @ 2.80 GHz,GTX 1050Ti GPU,16 GB RAM,使用Pytorch 1.10.0框架训练联邦学习模型,并使用gmpy2 python扩展模块实现Paillier加密。网络结构采用由3个3×3的卷积层、2个全连接层组成的卷积神经网络(Conventional Neural Network,CNN)。实验数据集采用一个包含60 000个训练样本和10 000个测试样本的手写数据集MNIST,每个样本是一个28×28的灰度数字图像。联邦学习中的超参数设置如表1所示。

表1 联邦学习超参数设置

6.1 准确率

模型准确率是衡量模型性能的重要指标之一。为了检验文中方案对计算结果准确性影响的优势,在表1所示的相同超参数下,将文中方案与相关方案的准确率相比较。

如图3所示,在MNIST数据集上,FedAvg算法[1]作为原始联邦学习算法的准确率约为97.6%,DP-FL算法[20]由于在训练时向参数添加高斯噪声,导致模型准确率降低至约92.9%,PPDL算法[10]使用Paillier同态加密保护模型参数,算法的准确率达到约97.3%,与FedAvg算法的准确率接近。CEEP-FL算法[14]使用非交互式零知识证明同态加密机制NIZKP-HC和梯度更新过滤机制,阻止上传与协作收敛趋势不相关的本地更新,因此模型收敛效率进一步提高,最终模型准确率达到约98.1%。本方案使用改进的Paillier同态加密保护更新参数,设计一种梯度过滤压缩算法,剔除每次更新过程中优化方向与全局优化方向不相关的梯度,模型准确率达到约97.9%。尽管略逊于文献[14],但本方案通过梯度过滤压缩算法,模型收敛速度得到明显提升。

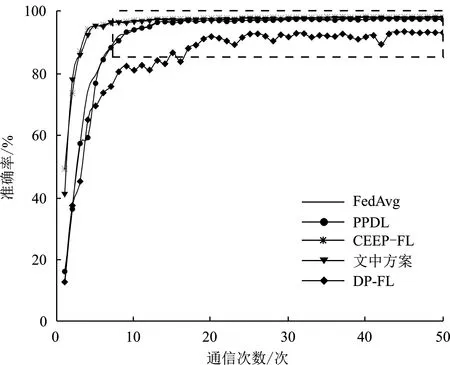
(a) 准确率对比

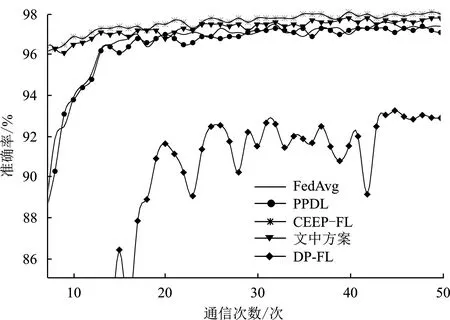
(b) 图(a)局部细节放大图

6.2 通信开销

通信开销是联邦学习的瓶颈之一。为了检验文中方案通信开销的优势,实验比较不同算法在相同数量的客户端环境下的通信开销。文中实验将基于加密的联邦学习方案PPDL算法[10]和CEEP-FL算法[14]作为对比方案,其中模型更新参数由双精度浮点数格式表示。如图4所示,在一轮全局更新中,随着模型权重的增加,由于PPDL算法和CEEP-FL算法首先对所有明文参数同态加密,然后上传服务器,因此二者有着较高的通信开销。该方案通过自然压缩算子将密文进行量化在上传服务器,相比PPDL算法减少约70%的通信量。

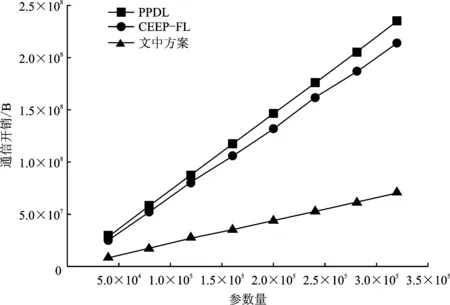
图4 不同方案的通信开销对比

表2给出了在给定模型精度下不同方案的具体通信开销。当模型精度在MNIST数据集中达到约95%时,PPDL算法每个客户端通信开销约276.48 MB,而CEEP-FL算法由于减少了通信次数,将通信开销减少到约224.64 MB。文中方案不仅过滤不相关的梯度更新减少通信次数,而且使用自然压缩算子量化密文,通信开销仅约有172.84 MB。

表2 每个客户端达到目标精度所需的通信开销 MB

6.3 计算开销

如图5所示,将文中方案与原始Paillier同态加密算法PPDL[10]和基于非交互式零知识证明的同态加密算法CEEP-FL[14]在不同长度密钥下的运行时间进行比较。由于PPDL算法和CEEP-FL算法的加密操作都需要两次大素数指数模乘法运算和一次模乘法运算,而文中方案只需要两次基本运算,因此本方案的加密时间相对较小,且随着密钥长度的增加,文中方案的优势更加明显。对比解密时间,PPDL算法和CEEP-FL算法的解密操作都需要两次较大的大素数指数模乘法运算和3次模乘法运算,而文中方案只需要一次较大的大素数指数模乘法运算和两次模乘法运算,略显优势。

(a) 加密时间

(b) 解密时间

7 结束语

针对联邦学习中的数据隐私保护的安全与效率问题,通过改进Paillier同态加密算法,并设计一种梯度过滤压缩算法,提出了一种安全高效基于同态加密的联邦学习隐私保护方案。由于将加密阶段的大指数模乘法运算简化为基本运算,减少了本地加密运算所需的计算成本;同时,通过梯度过滤压缩算法对更新参数进行过滤压缩,有效地降低了通信开销。安全性分析表明,方案具有不可区分性、数据隐私性和模型安全性等特性。实验结果显示,文中方案在模型准确率、通信开销和计算开销方面具有明显优势。