面向医疗数据的隐私保护联邦学习架构
王 波,李洪涛,王 洁,郭一娜
(1.太原科技大学 电子与信息工程学院,山西 太原 030024;2.山西师范大学 数学与计算机科学学院,山西 太原 030039)
1 引 言
随着人工智能、大数据、物联网等前沿技术应用于医疗行业,大量医疗数据随之生成[1]。对医疗数据进行分析、挖掘可以促进医疗行业的发展和革新。例如,借助机器学习算法对医疗数据进行挖掘、分析,可以提高模式的分析能力、非结构化数据的分析、预测能力和可追溯性,辅助医疗决策[2]。然而,这些数据通常包括患者的身份信息、患病信息、社会关系等敏感数据,一旦被恶意攻击者窃取或操控,将会严重危害患者的安全。近年来,医疗数据的隐私泄露问题引起了广泛的伦理以及法律关注。因此,探索医疗数据的隐私保护策略具有重要的现实意义[3-4]。
出于数据安全和隐私的考虑,不同医疗机构之间存在数据屏障,无法实现数据的安全共享[5]。此外,各机构独立的训练模型无法达到全局优化。针对以上问题,谷歌提出了一种去中心化的分布式机器学习框架——联邦学习(Federated Learning,FL)[6],将原始数据保留在节点上进行本地训练,训练好的模型上传给中央服务器,服务器聚合模型后再下发给各节点,从而将数据共享问题转化为模型共享问题,这使得一些敏感数据能够在“不出域”的情况参与训练,很大程度解决了隐私泄露问题。通过联邦学习,将各个医疗机构的“数据孤岛”联合起来协同训练的全局模型精度更高、泛化性更强[7]。然而,联邦学习过程中仍存在隐私泄露的风险:半诚实或恶意的参与方加入训练极易导致隐私泄露[8];恶意攻击者可以从共享模型参数中反推出参与者的部分敏感信息[9];服务器端返回的全局模型中会携带一些规律信息,攻击者可以推测出训练集参与方或训练集原始样本,且全局模型也可能是一个已经被投毒者“篡改”的模型,其学习模型不仅准确率低且会泄露用户的隐私[10]。
针对以上问题,文中旨在解决医疗数据在联邦学习中的以下3个挑战:首先,根据医疗数据的分布特征,选择合适的机器学习模型提高训练模型精度;其次,如何在保证数据高可用性的前提下增强数据的隐私保护力度;最后,如何在隐私保护技术产生的额外通信开销和联邦通信效率中取得平衡。
因此,文中基于同态加密技术提出了一种面向医疗数据的联邦学习隐私保护架构(Homomorphic Encryption Federated Learning for Privacy-preserving and Security,HEFLPS)。在模型性能、隐私保护和通信效率之间取得平衡,更适用于医疗数据场景。主要贡献如下:
(1) 提高了模型的训练精度。文中搭建了卷积神经网络(Convolutional Neural Network,CNN)模型,在新型冠状病毒(Corona Virus Disease 2019,COVID-19)数据集和MNIST手写数字数据集上均表现出较好的性能。
(2) 增强了联邦学习的安全性和隐私性。在模型共享阶段,采用同态加密技术对用户共享的训练模型进行加密,可以在不损失模型训练精度的情况下确保共享模型的安全性和隐私性。
(3) 降低了恶意客户端加入训练的可能性。结合Schnorr零知识证明(Zero-Knowledge Proof,ZKP)身份认证构建了身份认证模块,确保了参与训练的客户端身份的真实可信性。
(4) 弥补了同态加密带来的时间开销大的弱点。采用消息确认(ACKnowledgement,ACK)机制将离线或无响应用户暂时剔除,解决了用户在训练过程中退出的问题,提高了通信效率,缩短了等待同步聚合的等待时间。
2 相关工作
医疗数据共享是各个医疗机构间合作的基础,但其涉及到的隐私问题也是阻碍机构间数据共享的主要因素之一[11]。因此,解决联邦学习中信息泄露问题十分必要。相关的研究方法主要分为两类:一种是加密技术,包括安全多方计算[12](Homomorphic Encryption,HE)[13]和同态加密(Secure Mul-tiparty Computation,MPC);另一种是在模型参数中加入噪声,如差分隐私(Differential Privacy,DP)[14]。
FANG等[15]采用安全多方计算提出了一种在云计算中具有强大隐私保护作用的高效联邦学习架构,通过设计有效的优化策略提高学习效率,并表明该方案对于“诚实且好奇”以及“相互勾结”的服务器是安全的。但安全多方计算存在“信任问题”和“通信量问题”,同态加密则可以较好地解决上述问题。于是,KU等[16]将同态加密应用在由物联网设备收集的医疗数据隐私泄漏问题中。数据加密上传到雾节点,雾节点与云服务器协作完成模型的训练,提高了方案的鲁棒性,并解决了加密数据计算成本和存储成本高的问题。此外,JIANG等[17]提出了一种基于混合差分隐私和自适应梯度压缩的联邦学习框架,更适应于工业环境中的边缘计算,有效防止隐私数据受到推理攻击的威胁。
然而,差分隐私技术需要在数据或模型参数中添加随机噪声来实现隐私保护,将会导致训练的模型不够准确,最终导致训练精度不高[18]。相比之下,加密机制借助多方安全计算、同态加密等技术能够在提供隐私保护的同时保持模型的准确性,适用于参与方少、对准确性要求较高的场景。然而,密码学技术会造成协同训练效率低、存储和时间开销大等问题,且对参与方是否在线要求较高[19]。
由此可见,联邦学习系统所采用的隐私保护技术各有优劣,需要根据具体的应用场景选择适当的技术设计高效、实用的隐私保护方案。文中针对医疗数据的特殊性,设计了一种新的联邦学习架构,实现了隐私保护、模型性能和通信效率之间的平衡。
3 背景知识
3.1 联邦学习

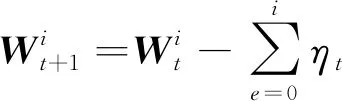
(1)

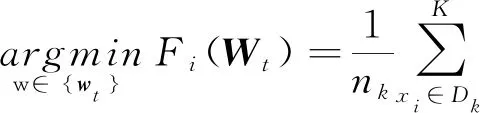
(2)
其中,nk表示客户端数量。
3.2 Paillier同态加密
同态加密是指对明文进行环上的加法和乘法运算再加密,与加密后对密文进行相应的运算,结果是等价的[21]。Pallier同态加密是一种满足加法同态的部分同态加密方法[22],由密钥生成、加密和解密3个阶段组成。
(1) 生成密钥。 令公钥为(n,g),对应的私钥为(λ,μ),有
λ=lcm(p-1,q-1) ,
(3)
μ=(L(gλmodn2))-1modn,
(4)
其中,n为公钥长度;g的阶是n的倍数;p和q为两个素数,满足gcd(pq,(p-1)(q-1))=1;lcm代表最小公倍数;L(x)=(x-1)/n。
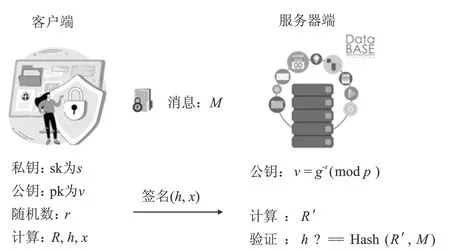
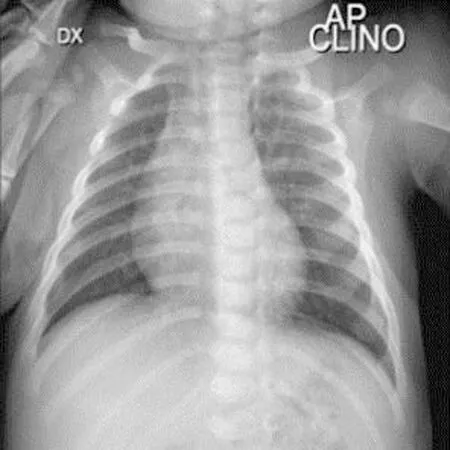
(2) 加密。 令密文和明文分别为c c=(gmrn)modn2。 (5) (3) 解密。 私钥的解密过程为 m=L(cλmodn2)μmodn。 (6) 文中基于Pallier同态加密技术提出了一种高效的联邦学习隐私保护方案,系统架构如图1所示。采用同态加密技术对中间参数进行加密处理,提高了模型的安全性和隐私性;利用Schnorr零知识身份认证技术对客户端进行身份认证,确保了用户身份的真实性;使用消息确认(ACK)机制使服务器端对参与用户进行离线监测,并及时删除离线用户,减少了通信等待时延。总体算法伪代码如算法1所示。 图1 HEFLPS系统结构图 HEFLPS主要执行步骤如下: (1) 客户端选择。 中央服务器将通过身份认证的用户Ck设定为参与本轮训练的客户端。 (2) 广播。 服务器端通过消息确认机制剔除离线用户并筛选下一轮参与训练的用户Cnew。 重复以上步骤,直到迭代t轮停止。 算法1HEFLPS算法描述。 输入:客户端集合C={c1,c2,…,ck},本地数据集D={di} 服务器端: 初始化 从通过身份认证的用户kclients⊂C中随机选择一些参与训练 ① 循环 ④ if用户cm返回ACK,则加入C中组成一个新的用户集合Cnew={cm1,cm2,…,cmk} ⑤ else认为用户离线,不参与本次训练 ⑥ 循环结束 客户端: ⑦ pk,sk← 生成Paillier密钥对(一次一密) ⑧ 循环 ⑨ 更新本地模型Wi+1←Wi-η∇fi 4.2.1 模型参数加密 联邦学习在模型传输过程中,模型参数会暴露给中心服务器,中心服务器下发的全局模型参数也会被每个客户端获取。攻击者可以发起重建攻击(Reconstruction Attacks)[23],通过共享的参数反向推断出原始数据,获取用户的隐私信息。针对该问题,文中基于Pallier同态加密技术提出了保护隐私的联邦学习架构,对中间过程交互的模型参数进行加密,从而实现模型参数的隐私保护。但Paillier同态加密只能实现密态加法运算,若出现乘法运算,文中则通过泰勒展开[24]将乘法运算以多项式相加的形式替换后,再进行同态加运算。 设有xi个数据,传输的加密模型参数为[W],对数损失函数可以表示为 (7) 对于任意的函数f(θ),在θ=0处的泰勒展开式为 (8) 当f(θ)为对数损失函数,即f(θ)=log(1+exp(-θ)),在θ=0处的泰勒展开表达式为 (9) 文中使用二阶多项式来近似对数损失函数,将θ=[W]Tx代入上式,并代入式(9),得到: (10) 对上式求导,得到损失函数关于参数[W]的加密梯度值为 (11) 4.2.2 Schnorr零知识身份认证 如果恶意攻击者获得用户的公钥,并对数据进行解密后添加随机扰动噪声,将导致计算无意义或使服务器无法分辨接收到的结果正确与否。因此,验证客户端身份的真实性也十分必要。 传统的认证机制包括两个实体,即用户和服务器。服务器拥有所有用户的身份信息,因此很容易获得用户的信息。同时,用户发送给服务器用来身份验证的签名信息也可能被攻击者截获,从而计算出用户的身份信息,造成用户的信息泄露。文中提出的基于Schnorr零知识的身份认证机制则可以较好地解决以上问题。其中零知识证明[25]是指证明者能够在不向验证者提供任何有用信息的情况下,使验证者相信某个论断是正确的。Schnorr机制[26]是一种基于离散对数难题的零知识证明机制。文中的认证模块中,客户端C需向服务器端S证明自己拥有对身份信息的数字签名(h,x),而不泄漏有关h和x的任何有用信息以证明身份的真实性。公共参数:p为任意素数,生成元为g,公钥为v=g-s(modp)C,拥有的私钥为s。其认证过程如图2 所示,具体描述如下。 图2 Schnorr零知识身份认证过程 (2) 服务器端S验证。 计算R′=gxvh(modp),并验证h=Hash(R′,M),如果相等,则身份验证通过;否则,不通过。 验证过程为证明h=Hash(R′,M)。首先,证明R′=R。将v代入R′中,得 R′=gxg-sh(modp)=gx-sh(modp) , (12) 又因为x=r+hs,得r=x-hs,代入式(1),得R′=gr(modp),故R′=R。 在客户端,同态加密的加密和解密时间以及模型的训练时间是一次迭代时长的主要组成,其中,20%的时间用于数据传输和等待模型参数聚合返回[27]。在得到来自中央服务器返回的全局模型之前,任何客户端均无法进行下一次迭代。 在服务器端,由于同步障碍,参与训练的客户端之间的资源和数据异质性可能会导致客户端不同的响应延迟,这通常被称为掉队者问题(Straggler Problem)[28]。设客户端Ci的响应延迟为Rt,则服务器的等待延迟为 Rt=max(R1,R2,…,R|C|) 。 (13) 从式(13)可知,在每一轮训练中,服务器的等待时延为客户端中最大的响应时延,即由最慢的客户端决定,需等待其完成训练后才能进行聚合更新,这是造成通信效率低的主要原因之一。 为了解决服务器端无效的通信等待时延问题,文中对响应时间过长和离线的用户分别进行处理,如算法2所示。 挑选客户端的规则:设第t轮更新中所挑选的活跃客户端集合为C={c1,c2,…,ck},每个客户被选中的概率设为1/τ。 中央服务器S对集合C中每个用户发送确认消息,如果接收到用户的ACK,则将该用户添加到Cnew中;否则,认为该用户离线不参与本轮更新(离线用户仍可参加下一轮迭代)。在Cnew中,将响应时间最长的用户被选中的概率降为其原来概率的1/k,Pτ可表示为 (14) 算法2服务器端异步聚合。 输入:客户集C={c1,c2,…,ck} 输出:更新客户集C′new 初始化 随机选择用户kclients⊂C ① 循环 ② 通信轮数t ③ 广播 ④ ifcm用户返回ACK ⑤ 更新的用户集Cnew={cm1,cm2,…,cmk} ⑥ 标记返回ACK最长时间的用户T_Max(Cnew) ⑦ 减少该用户下一次参与训练的概率为(1/k)T_Max(Cnew) ⑧ else if ⑩ end if 对HEFLPS的安全性分析如下: (1) 同态加密隐私保护机制。首先,联邦学习通过将数据保留在本地的形式进行训练学习,避免了数据暴露给第三方,保证了数据的安全性和隐私性;其次,客户端向服务器端发送的是加密后的模型参数,由于Paillier同态加密方案满足CPA安全性,即使攻击者截获了加密后的模型参数,也无法获取到明文数据,实现了“原始数据不出域,数据可用不可见”。 (2) 客户端身份认证。不诚实或恶意的客户端可能会共享无效数据或有害数据,文中通过Schnorr零知识身份认证技术确保只有合法的客户端才能参与训练。假设C没有私钥sk,那么C很难构造一个签名(h,x)以通过S的验证。由于哈希函数和离散对数的困难性,S也很难根据(h,x)反推出C的私钥。 (3) 诚实且好奇的服务器。由于客户端上传的是加密后的模型参数,因此在服务器聚合过程中,数据对服务器是“不可见”的。而且每次迭代都会更改密钥对,即使攻击者破解了几轮训练结果,也无法获得最终结果。 综上所述,文中所提的HEFLPS框架能够满足数据的隐私性和安全性要求。 本节以备受关注的新冠肺炎检测为例,使用COVID-19 Radiography(https://www.kaggle.com/datasets/preetviradiya/covid19-radiography-dataset)数据集以及对照数据集MINIST(http://yann.lecun.com/exdb/mnist/)在分类准确率、平均加解密时长、客户端数量对准确率的影响、通信时延、隐私保护5个方面对HEFLPS架构性能进行实验分析,验证该架构性能的优越性。 5.1.1 实验环境 仿真环境硬件平台基于3080ti GPU和64 GB内存,软件平台基于python3.7上运行Pythorch(v1.11.0)、操作系统为64-b Ubuntu 18.04。 每一轮实验从模拟的客户端设备中任意挑选5台参与训练,学习率为0.005,每一次本地训练迭代次数为3次,全局迭代次数为100次,其他实验参数的设置如表1所示。 表1 实验参数设置 5.1.2 实验数据集 文中采用kangle数据集网址中胸部X射线图像数据集(COVID-19 Radiography Dataset),其中包括3 616 例新冠肺炎阳性病例以及10 192例正常肺部图像,每张大小为299×299像素,如图3所示。文中实验选取3 432张图片(80%)作为训练集,858张图片(20%)作为测试集,其中正常图像(标记为0)和新冠肺炎阳性病例图像(标记为1)以1.00∶1.15进行混合,构成文中的COVID-19数据集。 (a) 新冠肺炎阳性肺部图像 (b) 正常肺部图像 此外,文中采用机器学习中被广泛用于图像分类任务的手写体数字图片数据集MNIST作为对照数据集。如图4所示,该数据集包含60 000张训练图片和10 000张测试图片,每张大小为28×28像素。 (a) MNIST手写体整体图 (b) MNIST手写体部分放大图 实验使用卷积神经网络作为训练模型,由2个卷积层(卷积核分别为8×8和4×4,步长为2)、2个最大池化层、1个全连接层和1个输出层组成,使用的激活函数为ReLU。分别在两个数据集中的测试准确率如表2所示。实验结果显示,文中CNN模型在两个数据集上均能达到较高的准确率。 表2 不用数据集的模型分类准确率 文中采用联邦平均FedAvg模型聚合方法进行模型聚合,分别在COVID-19和MNIST数据集上与传统的集中学习进行对比,如图5所示。集中学习的参数设置:客户端数量和每一轮挑选的参与训练的客户端数k均设为1,即只有1个客户端设备参与的联邦训练等价于集中式学习。其余参数配置与FedAvg一致。实验结果表明,FedAvg的准确率能达到与集中学习近似的准确率。 图5 FedAvg与集中式学习分类准确率的比较 在Paillier同态加密中,随着密钥长度的增加,安全级别会提高,但随之而来的时间开销也会增加。因此,文中需选择适当的密钥长度,来权衡安全级别和时间开销。此外,为了提升安全级别,在每一轮训练过程中都会重新生成密钥对。这样,即使某一轮密钥被破解,也不会影响整个训练过程的安全性,实现更高级别的数据安全。不同密钥长度对应的时间开销如图6所示。 如图6所示,实验分别计算了密钥长度为256、512、1 024、2 048 bit的平均加解密时长。可以看出,随着密钥长度的增加,时间呈现聚增现象。考虑到同态加密的安全性越高,相应的时间开销也越高的特性,文中采用密钥长度为512 bit对模型参数进行加密。 (a) COVID-19 (b) MNIST 文中选择不同数量的客户端k∈{5,10,15,20},进行分类准确率和通信时长的对比实验,如图7、8所示。由图7可知,当客户端数量较少时会产生较高的平均分类精度,同样也能在较多的客户端上实现较高的平均分类精度,相差约为1.9%,说明用户数量对文中所提架构的分类精度影响不大,同时也说明用户的离线对整体的模型精度影响不大。显然也能从实验结果看出,客户端数量越少,收敛速度越快。并且由图8可知,随着客户端数量的增加,联邦通信时长也在明显增加,当k=5时,每个用户的时间消耗最少。因此,文中选取客户端数量k=5作为实验基准。 (a) COVID-19 (b) MNIST 图8 不同客户端数量通信时长比较 通信总时间主要来自模型加、解密的时间和等待客户端返回结果的时间。而联邦学习产生的等待时延主要由最慢的客户端参与训练的时长决定,因此。客户端的选择对通信时延的影响很大。文中所提方案的通信时长随客户端数量的变化如表3所示。 表3 优化前后通信开销比较 s 结合表3和图8得出,当客户端数量增加时,时间开销近似线性增加。在COVID-19数据集中,当C=5时,时间缩短了300 s,而当C=10时,时间缩短了445 s。同样在MNIST数据集中,随着客户端数量的增加,缩短的时间也越多,即文中方案对于客户端较多的情况体现出的优势更加明显。因为随着客户端数量的增加,客户端出现故障的可能性也在增加,更大地缩短了服务器端的无效等待时间。 文中将Paillier同态加密和差分隐私技术分别在两个数据集上对模型准确率进行对比实验,如图9所示。 (a) COVID-19 (b) MNIST 实验结果表明,差分隐私因其对数据加入了噪声会使数据可用性降低导致分类准确率降低;而同态加密则能保持和无隐私保护的联邦学习一致的准确率,说明同态加密可以在提供数据高安全性的情况下,依然能保证其较高的准确率以及数据可用性。 以上实验结果证明了文中所提的HEFLPS架构在准确率和时间开销方面的优越性,且能够在高准确率、低时延的情况下实现较强的隐私保护性能。 文中基于同态加密提出了一种高效的医疗数据隐私保护联邦学习架构-HEFLPS。分别对联邦学习参与方进行安全身份认证以及对模型参数进行隐私保护,并结合消息确认机制降低了联邦通信开销。在COVID-19数据集以及MNIST数据集上的实验结果表明,文中所提架构能在保持较高分类准确率的同时实现隐私保护。但由于同态加密存在密文爆炸、密钥过大和运行效率低等问题,在未来工作中,将进一步设计效率更高的隐私保护联邦学习架构,更好地应用于医疗大数据的实际应用场景中。4 系统模型
4.1 总体架构

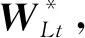

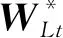
4.2 模型构建
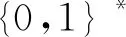
4.3 通信开销
4.4 安全性分析
5 实验与分析
5.1 实验设置



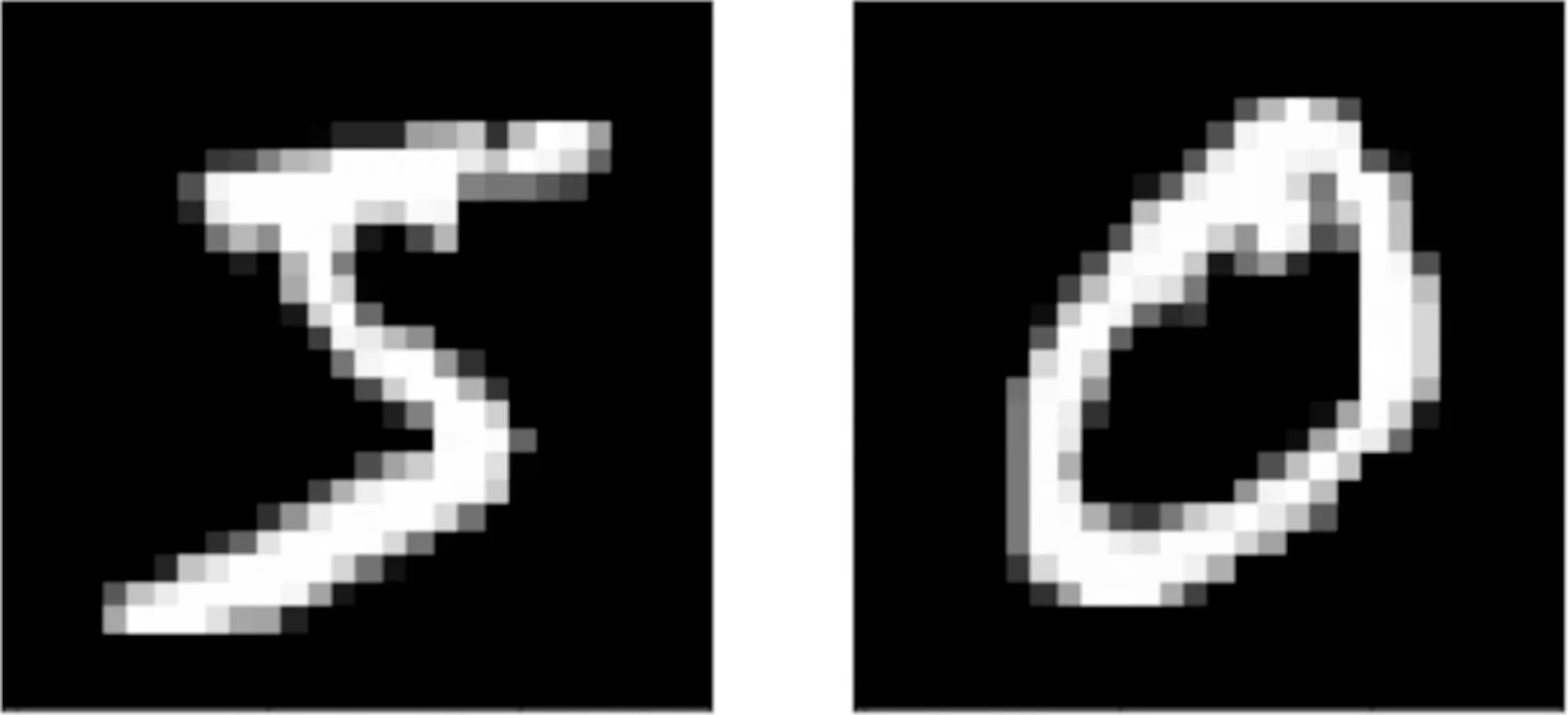
5.2 模型准确率分析
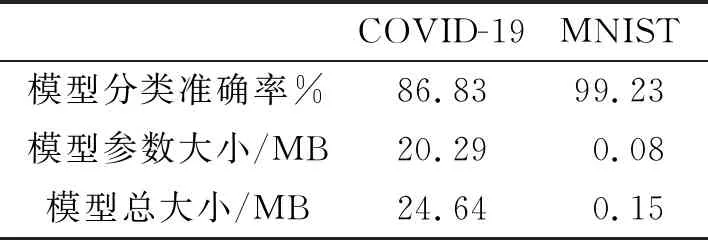

5.3 平均加解密时间

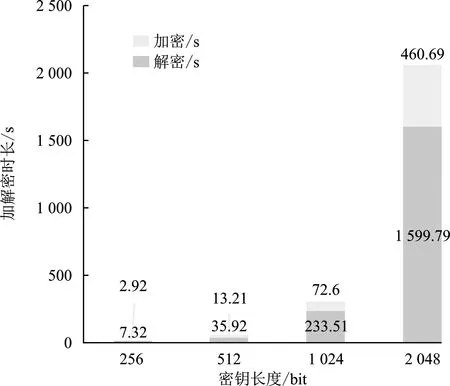
5.4 客户端数量对实验性能的影响

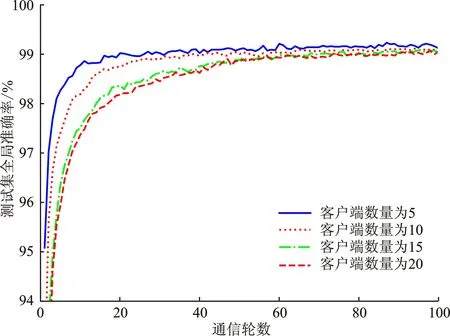

5.5 通信时延
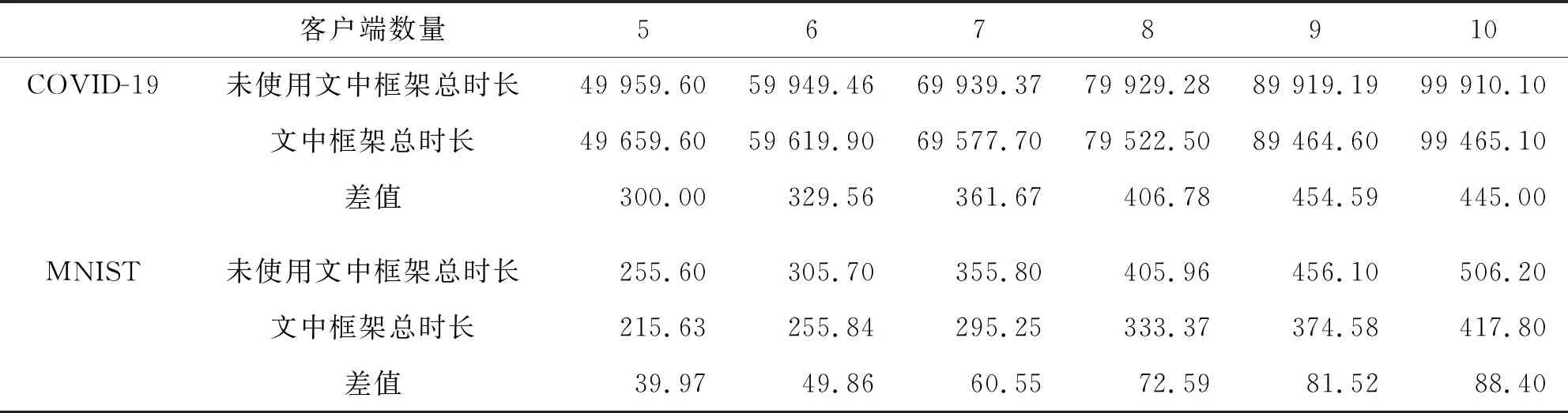
5.6 隐私保护
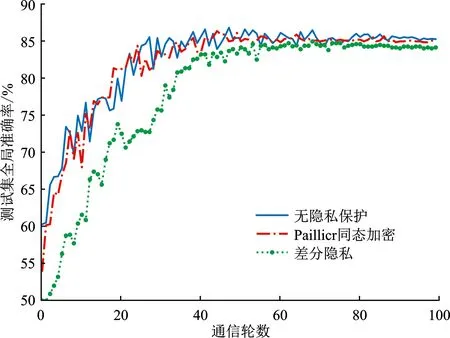
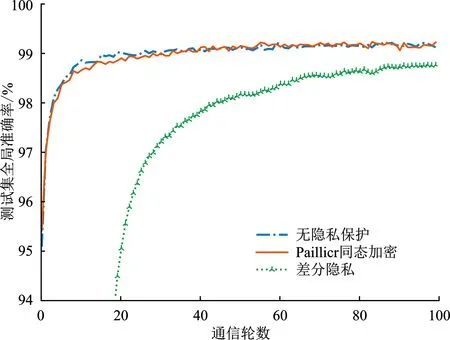
6 结束语

