融合空间聚类与结构特征的点集配准优化算法

胡 欣,向迪源,秦 皓,肖 剑

(1.长安大学 能源与电气工程学院,陕西 西安 710064;2.长安大学 电子与控制工程学院,陕西 西安 710064)

1 引 言

点集配准是计算机视觉和模式识别领域的关键问题和瓶颈技术,将多源、多时段、多视场的图像点集配准就是寻找空间变换能够最优对准两幅图像[1-3]。为寻找准确的点与点的对应关系,点集配准根据变换方式的不同可分为刚性配准和非刚性配准[4]。刚性点集配准的变换方式包括缩放、平移和旋转,属于全局变换且涉及参数少。而非刚性点集配准的变换方式往往是未知的、复杂的,且难以建模,通常包含较多的变换参数,无法以简单的参数化方式建模[5-6]。

近年来,将密度估计算法生成的模型引入到非刚性匹配中的方法被广泛研究。TSIN等[7]和GLAUNES等[8]首先提出用函数对点集进行建模,函数中拥有平滑机制,使得算法在处理噪音和异常值时具有优势,但模型函数的选择依旧有待优化。在此基础上,JIAN等[9]引入了高斯混合模型(Gaussian Mixed Model,GMM)搭建模型框架,但仍存在初始值敏感的问题。为此,CAMPBELL等[10]提出了使用支持向量参数拟合GMM模型数据,但算法性能在复杂变换函数中受限。由MYRONENKO等[11]首先提出的相干点漂移(Coherent Point Drift,CPD)算法是基于GMM和期望最大化(Expectation-Maximization,EM)算法,在点集配准中被越来越多的使用,其实质是将匹配问题转换为最大似然估计问题,由于存在初始值敏感和局部极值问题,研究者基于CPD算法提出了许多改进算法[12-15]。JIAN等[16]将匹配的思想从拟合高斯混合模型扩展到对齐两个高斯混合模型。MA等[17]提出了基于高斯混合模型的矢量场一致性(Vector Field Consensus,VFC)算法。以上算法在高斯混合模型解决点集对应问题中仅考虑了全局运动一致性约束条件,没有考虑局部特征。随后,YANG等[18]提出了混合特征的全局和局部混合距离-薄板样条方法(Global and Local Mixture Distance-Thin Plate Spline,GLMDTPS)。MA等[19]提出了保持全局和局部结构特征的点集对齐算法(Point set Registration both Global and Local Structures,PR-GLS)。JIANG等[20]提出了基于离群点空间聚类的鲁棒特征匹配算法(Robust Feature Matching using Spatial Clustering of Applications with Noise,RFM-SCAN)。彭磊等[21]提出了考虑邻域信息和考虑全局与局部相似度测度的非刚性点集配准算法,算法利用点集局部特征的一致性作为先验约束,将寻找正确匹配点过程转化为概率密度来解决点集对齐问题。近年来,HIROSE[22]改进了CPD算法,并提出相干点漂移的贝叶斯公式(Bayesian formulation of Coherent Point Drift,BCPD),在贝叶斯公式中加入相干点漂移,增强了对目标旋转的鲁棒性。ZHU等[23]从期望最大化的角度提出了多视图配准问题的新解决方案。WANG等[24]提出空间相干匹配(Spatially Coherent Matching,SCM)算法,保持局部邻域结构的同时学习非刚性变换。以上算法中,样本点的局部特征选择和局部特征聚类是算法需要解决的关键性问题,当局部特征变化不稳定和变形严重导致大量异常值出现时,算法的性能和特征会产生差异。在混合模型的框架下,自适应地完成局部聚类和局部特征描述是基于GMM和EM算法完成点集配准的一种思路,也是笔者提出采用局部空间聚类和邻域结构特征的点集配准优化算法(Point set Registration using Spatial Distance Clustering and Local Structural features,PR-SDCLS)的出发点。

文中提出了一种新颖的融合全局与局部特征的高斯混合点集配准算法。主要贡献如下:

(1) 通过空间距离矩阵将预匹配聚类为多个运动一致性聚类和一个离群值聚类,并将离群值聚类中的匹配点删除,减小了算法的复杂度。

(2) 对一致性聚类子集分别使用高斯混合模型拟合和EM算法参数估计,避免了复杂的建模,提高了匹配精度和效率。

(3) 模型拟合的过程中,将描述子与空间距离相结合自适应对混合系数赋值,避免了考虑全局特征时局部特征信息丢失的问题。

2 高斯混合模型

2.1 点集配准与高斯混合模型

采用高斯混合模型GMM求解,实质是转换为概率密度估计问题。 令X={x1,…,xn}∈RD×N为模板点集,Y={y1,…,ym}∈RD×M为目标点集,将目标点集x作为高斯模型的质心,模板点集y为由GMM产生的数据点。高斯混合模型的概率密度函数为

(1)

其中,当模板点集xi与目标点集yj是D维时,μ为期望,Σ为协方差,则有

(2)

其中,当模板点集xi与目标点集yj是二维时,μ为期望,σ为方差,则有

(3)

由于以上的概率密度函数无法体现目标点集与模板点集中点的对应关系和变换关系,因此在高斯混合模型中引入隐变量Z对模板点集xi与目标点集yj的对应关系进行描述。具体如下:

Z={zm∈NN+1:m∈NN} ,

(4)

其中,

假设离群点的分布为均匀分布1/b。

引入变换函数f:RN→RN,作为模板点集中的点映射到目标点集中的点的函数,将每个高斯模型的质心由模板点xi替代为模板点映射到目标点集平面的点f(xi)。

综上,由于模板点集xi与目标点集yj均为二维,因此点集对应关系和变换关系的混合模型的概率密度函数表示为

(5)

其中,θ={f,σ2,γ},为未知参数集;γ∈[0,1]代表隐变量的边缘分布,即P(zm=N+1)=γ。混合系数πmn通常采用等概率赋值,即πmn=1/N。采用贝叶斯准则估计θ的一个最大后验解,等价于最小化如下的负对数后验:

(6)

对式(6)求取最大后验解,变换函数f将从最优解θ*中直接获取。

2.2 参数估计的EM算法

EM算法是通过迭代求L(θ)=log (Y|θ)的极大似然估计。每次迭代包含两个步骤:①E步为求期望 ;②M步为求极大值。省略掉负对数后验函数L(θ|Y)独立于参数θ的项,得到完全数据对数后验函数Q,具体表示为

(7)

(1) E步:采用θold求出隐变量的后验概率。令PM×N为一个M×N的后验概率矩阵,pmn指ym与xn在当前估计出的变换函数f下的吻合程度:

(8)

在Q函数中考虑与变换函数f相关的项,得到如下一个正则化风险泛函:

(9)

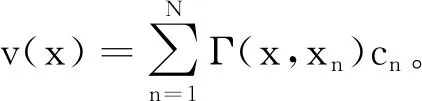
C(Γdiag(1TP)+λσ2I)=YP-xσ2diag(1TP) ,

(10)

其中,1表示一个全1的1×m列向量。将P,λ,σ2等参数带入式(10),求出系数矩阵C后,即可求出位移函数v(x)和变换函数f(x)。

3 改进方法

非刚性配准中,针对数据退化程度增加导致算法性能下降严重的问题,文中提出在考虑全局和局部结构特征的高斯混合模型框架内,引入点集的空间距离聚类和邻域结构特征,更好地解决点集配准问题。具体来说,就是通过距离进行分类,对每个子集估计混合密度来求解点集配准问题:任取一个点为中心点,并将这个点邻域内的所有点合并为一个新的子集。分别对每个子集拟合一个高斯混合模型,使其高斯密度的中心与另一个对应子集保持一致。同时,采用点集描述子的局部特征结合特征点与中心点的距离对混合模型每个组成部分的混合系数进行赋值,从而使得在配准时既做到了全局结构特征的匹配,又保持了局部结构特征。

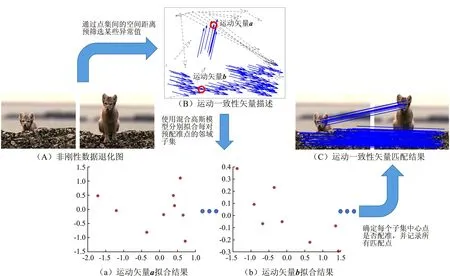
图1 算法的配准过程

文中算法的匹配过程如图1所示,对于两幅存在非刚性数据退化的图1(A)中,使用运动一致性矢量对其进行描述,如图1(B)所示,其中实线的运动一致性矢量代表了至少有一个运动矢量与其一致的运动矢量集合,虚线的运动矢量代表了离群的不具备运动一致性的一类。在具有运动一致性的矢量集合中,通过空间距离求出每个运动矢量的邻域,对每个邻域分别拟合高斯混合模型,图1(B)中运动矢量a拟合高斯混合模型的结果如图1(a)所示,运动矢量b拟合高斯混合模型的结果如图1(b)所示,剔除不具备运动一致性的运动矢量后的匹配结果如图1(C)所示。

在图1中,通过空间距离先剔除不具备运动一致性的运动矢量,同时求出每个运动矢量的邻域,接着让每个邻域分别拟合高斯混合模型,在此基础上,为了充分挖掘局部结构特征,引入形状上下文特征,并将匈牙利算法、χ2度量及空间距离相结合修正了高斯混合模型的比例系数。该方案适用于对精度要求较高的点集对齐问题。此外,与现有的相关方案相比,该方案具有更好的鲁棒性和效果。综合性能分析和仿真结果验证了该方案的有效性和鲁棒性。

3.1 点集空间距离聚类

A={ai=(xi,yi,mi)T,i=1,…,H} 。

(11)

为了增强运动一致性,设计一个加权距离,表示如下:

d(ai,aj)=φ(xi,xj)+φ(yi,yj)+ωijφ(mi,mj) ,

(12)

其中,ωij为权重参数,定义为ωij=1+γexp(-min{φ(xi,xj),φ(yi,yj)}),γ为正数,用于增强相邻点间的运动一致性,文中由经验取γ=10。φ(x,y)为距离函数,文中采用欧式距离。

因此,可以计算出H×H的距离矩阵D:

Dij=d(ai,aj) 。

(13)

首先,令μ为每个中心点邻域内的采样点与图片上总采样点的比率。然后,对距离矩阵按列进行归一化处理,把第i列中元素小于μ的元素所对应的行数的数据当作第i类分类,即第i个子集,共得到H个子集。

3.2 混合模型

令第i个子集内有Ni对点,其中模板点集为X′={x′1,…,x′Ni}∈RD×Ni,目标点集为Y′={y′1,…,y′Ni}∈RD×Ni,第i个子集配准的高斯混合模型的概率密度函数为

(14)

在式(5)中混合系数πmn表示目标点ym归属于高斯密度中心f(xn)的概率,通常采用等概率赋值,即πmn=1/N。但是,在非刚性点集配准问题中,挖掘局部结构特征并将局部结构特征融入混合模型也是至关重要的。因此文中采用形状上下文(shape context)作为子集的特征描述子,将匈牙利算法结合χ2度量与子集内观测点到中心点的距离相结合来初始化混合系数π′mn,目标点y′m有对应的模板点,具体表示为

(15)

其中,τ∈[0,1]为特征匹配可信度,I为y′m对应的模板点集,|I|为点集I的大小。

如果目标点y′m没有对应的模板点,那么对混合系数π′mn等概率赋初值为π′mn=1/(NiDmn)。混合系数π′mn能在配准时同时保持点集的全局与局部结构特征。结合式(8),可获得第i个子集的后验概率矩阵Pi:

(16)

得到协方差和离群点的比率为

(17)

一旦EM算法收敛,就能得到最优的变换函数f,此外也能得到内点的一个估计。首先在此处设置一个阈值TH,然后找到每一个模板子集的中心点和其对应目标子集的所有点的后验概率的最大值pimax。因此,一致集F表示为

F={i:pimax>TH,i∈NN} 。

(18)

由于改进的非刚性点集配准算法同时挖掘全局与局部结构特征,因此将其命名为基于空间距离聚类与局部特征的鲁棒点集配准算法(PR-SDCLS)。算法的具体流程见算法1。

算法1基于距离分类与高斯混合模型点集配准算法。

输入:两个点集X和Y,参数γ,λ,β,μ,TH

输出:一致集F

② 计算距离矩阵D

③ 根据比率μ求得H个子集

④ loopi=i+1

⑤ repeat

⑥ E步

⑦ 找到变形后模板点集f(X′)的特征描述子

⑧ 建立f(X′)与Y′之间的关系

⑨ 基于特征匹配和距离初始化混合系数π′mn

⑩ 更新后验概率p′mn

3.3 基于空间聚类的加速算法

在PR-SDCLS中,需要对每一个点及其邻域的子集拟合高斯混合模型,对于点集配准问题,尤其是三维点云来说,数据中点的数量极多,会造成计算复杂度过高导致计算上的不可行,为了解决这个问题,在算法2步骤②计算距离矩阵D之后,利用空间距离矩阵D,将假定的匹配自适应地聚类为多个运动一致性聚类和一个离群值聚类。在后续过程中,只需删除离群值聚类,并对多个运动一致性聚类中的点所对应的子集拟合高斯混合模型,此时得到H′个子集(算法2步骤③,删除了离群值聚类后,导致预匹配对减少,即H′≥H)。加速后算法具体流程见算法2。

算法2基于距离分类与高斯混合模型加速点集配准算法。

输入:两个点集X和Y,参数γ,λ,β,μ,TH,ε

输出:一致集F。

② 计算距离矩阵D

③ 根据距离ε和距离矩阵D,将假定的匹配聚类为多个运动一致性聚类和一个离群值聚类,删除离群值聚类

④ 根据比率μ求得H′个子集

⑤ loopi=i+1

⑥ repeat

⑦ E步

⑧ 找到变形后模板点集f(X′)的特征描述子

⑨ 建立f(X′)与Y′之间的关系

⑩ 基于特征匹配和距离初始化混合系数π′mn

4 实 验

为了估计PR-SDCLS算法的性能,采用3个不同的实验条件:非刚性点集、调整加权距离和调整混合系数。使用MATLAB代码实现了改进的算法,实验配置为2.50 GHz Intel(R) Core(TM) i5-7200U CPU,内存为4.00 GB的笔记本。

公共数据集采用两个不同结构模型[25-26]:鱼和汉字“福”。图2所示为数据集在旋转、变形、噪声,遮挡和异常值5方面的数据退化结果。其中,旋转退化是完成非线性变形,并使用地真校正,分为6级旋转,即0°、30°、60°、90°、120°和180°;变形退化,分为5级变形,即0.02、0.035、0.05、0.065、0.08;噪声退化,即为加入噪声,分为6级噪声级别,即0、0.01、0.02、0.03、0.04、0.05;遮挡退化,是完成适度非线性变形后随机删除一定量数据,分为6级遮挡级别,即0%、10%、20%、30%、40%和50%;异常值退化,是进行适度非线性形变后加入服从均匀分布的不同比例的异常值,分为5级异常值比例级别,即0、0.5、1、1.5、2。实验每种退化类型对应生成100个样本作为点集配准的目标数据。

图2 不同结构模型数据集的数据退化结果

4.1 非刚性配准的结果

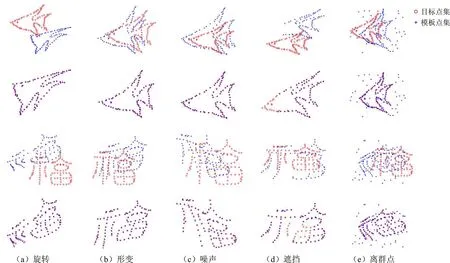
图3 PR-SDCLS算法在不同退化类型下的配准结果

将文中PR-SDCLS算法与4类性能良好的PR-GLS、RFM-SCAN、VFC、CPD算法比较,图4给出了在不同退化类型下算法配准结果的平均误差,图中每种退化类型使用退化参数作为横坐标,平均误差作为纵坐标。旋转退化中PR-GLS、RFM-SCAN、CPD、PR-SDCLS算法在旋转角度小于30°时可以取得相似的效果,但在旋转角度大于30°时,PR-GLS、RFM-SCAN、VFC、CPD配准效果迅速退化,文中提出的PR-SDCLS算法却并不受这类数据退化的影响。变形退化中,VFC的配准效果远差于其他4类算法,RFM-SCAN在变形程度大于0.05时,配准效果迅速退化,PR-GLS、RFM-SCAN、PR-SDCLS在任意变形程度下,都能取得相似的结果,所提PR-SDCLS仍然能取得最优的结果。噪声退化中,VFC并不受这类数据退化的影响,但它的配准效果明显差于其他算法,RFM-SCAN在噪声水平大于0.02时,配准效果迅速退化,PR-GLS、RFM-SCAN、PR-SDCLS在任意噪声水平下,都能取得相似的结果,所提PR-SDCLS算法仍然能取得最优结果。遮挡退化中,PR-GLS、RFM-SCAN、VFC、CPD随着遮挡比率的增大配准效果衰减明显,所提PR-SDCLS表现出了很强的鲁棒性。离群点退化中,VFC并不受这类数据退化的影响,但它的配准效果明显差于其他算法,PR-GLS、RFM-SCAN、PR-SDCLS在任意离群点和样本数量的比率下,取得的结果都相似,PR-SDCLS在任意比率下配准效果都明显优于其他算法。因此,PR-SDCLS算法通过有效保持点集的全局与局部结构特征,其对各类非刚性点集配准问题——无论是形变、噪声、离群点、旋转,还是遮挡,均能很好地解决。表1给出了在不同退化类型下算法配准结果平均误差的均值,文中PR-SDCLS算法至少降低了约1.477 1%的平均误差,最多降低了约72.454 8%的平均误差,验证了算法在非刚性配准中具备良好的性能和鲁棒性。

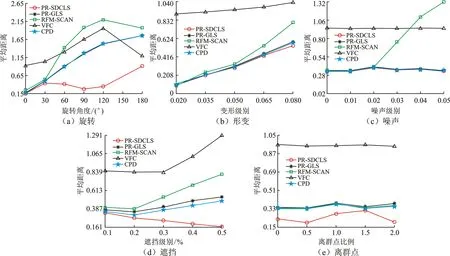
图4 算法在不同退化类型配准结果误差的平均统计性能

表1 算法在不同退化类型配准结果平均误差的均值

4.2 调整加权距离

调整加权距离测试PR-SDCLS算法性能,算法中引入运动矢量增强了运动一致性,但带来了冗余。为了测试加权距离的性能,调整4种不同的噪声观测数据集A和加权距离,分别为

(19)

图5给出了对应的平均距离曲线(分别用D12,D13,D23,D123表示ai=(xi,yi)T,ai=(xi,mi)T,ai=(yi,mi)T,ai=(xi,yi,mi)T时的平均距离),在不同变形中的平均误差的均值在表2中给出,文中PR-SDCLS算法不同A值时至少降低了约0.199 2%的平均误差,最多降低了约51.640 2%的平均误差,验证了算法在非刚性配准中具备良好的性能和鲁棒性。

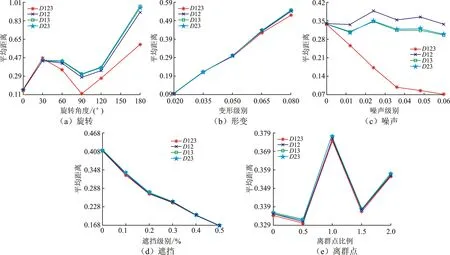
图5 PR-SDCLS算法在不同A值时在不同退化类型下配准结果误差的平均统计性能

表2 PR-SDCLS算法中不同P值在不同退化类型下平均误差的均值

显然,在任意变换情况下使用Pi=(xi,yi,mi)T的性能最好。噪声退化中Pi=(xi,mi)T和Pi=(yi,mi)T的性能相似,Pi=(xi,yi)T的性能最差,这和文中的预测一致,mi的引入增强了运动一致性。在其他退化中,Pi=(xi,mi)T和Pi=(yi,mi)T的性能相似,Pi=(xi,yi,mi)T的性能最好,但Pi=(xi,yi)T的性能并不是最差的。

可以得出结论:①特征点的空间位置xi和yi通常具有高度相关性。 使用运动矢量mi可以消除这种相关性,因此可以增加数据的可分性。 ②在同等维度1/2空间,mi的引入虽然可以增强运动一致性,但也造成了数据的冗余。 ③使用Pi=(xi,mi)T和Pi=(yi,mi)T能实现相似的性能,因为它们在数据空间中呈现相似的结构。 ④通过使用Pi=(xi,yi,mi)T,输入数据被放入更高的维度空间,通常可以进一步增加数据的可分性。因此,它能实现最佳的性能。

4.3 调整模型混合系数

测试PR-SDCLS算法中混合系数的性能,大多数初始化混合系数πmn采用等概率赋值设定为系数1;HORAUD等[12]提出的保持全局和局部结构特征的点集对齐算法中,通过形状上下文结合匈牙利算法对混合系数进行赋值,设定为系数2;文中采用π′mn,设定为系数3:图6给出了3个系数在不同退化类型的配准结果的误差统计。在不同变形中的平均误差的均值在表3中给出。对图6的结果分析,在数据形变程度不大时,3种系数可以取得相似的效果,但在数据形变程度较大时,使用系数3的性能最优,系数2的性能次之,系数1的性能最差。从表3可以看到,系数3在所有数据退化的情况下均明显优于其它两种系数,文中PR-SDCLS算法在不同混合系数的情况下至少降低了约0.138 9%的平均误差,最多降低了约14.453 6%的平均误差,验证了算法在非刚性配准中具备良好的性能和鲁棒性。

图6 PR-SDCLS算法中不同混合系数在不同数据退化类型下配准结果误差的平均统计性能

表3 PR-SDCLS算法中不同混合系数在不同退化类型下平均误差的均值

可以得出:①系数2和系数3作为高斯混合模型的混合系数并不是以一个先验进行赋值,而是依赖于具体数据进行赋值。因此系数2和系数3可以在配准时同时保持点集的全局与局部结构特征,从而达到更好的性能。但是系数1进行等概率赋初,没有考虑到数据的局部结构特征,仅依靠PR-SDCLS算法中的基于距离进行局部分类,显然不能取得最好的效果。②系数3跟系数2相比,系数3在保持局部结构特征时不仅引入了形状上下文作为特征描述子和匈牙利算法χ2度量,还引入了观测点到中心点的局部空间距离。因此系数3的性能优于系数1。

5 结束语

实验中,通过调整两类参数,在不同数据退化类型下算法至少降低了约1.477 1%的平均误差,最多降低了约72.454 8%的平均误差,且平均降低了约42.053 8%验证了算法在非刚性配准中具备良好的性能和鲁棒性。文中所提出的这种新颖的基于高斯混合模型的点集配准算法,融合了两个对应点集间稳定的局部和全局约束。由于引入空间距离分类,所提算法可忽略点集的复杂程度,将复杂和难以建模的点集有效分解为多个简单的点集拟合;同时采用了点集中特征描述符来提高模型拟合度。非刚性点集下配准的实验结果表明,文中算法在面对不同数据退化的点集配准结果良好,算法性能鲁棒性强、精度高。