新型电力系统动态负荷电能测量算法

胡涛,杜梦如,马建,王学伟,邓高峰

(1.国网江西省电力有限公司供电服务管理中心,南昌 330032; 2.北京化工大学 信息科学与技术学院,北京 100029)

0 引 言

随着我国构建新型电力系统,风能与太阳能等新能源大规模接入电网,新能源占比逐渐提高;工业领域中钢铁行业碳达峰行动、交通运输行业绿色低碳行动、电弧炉与高铁机车等大功率动态负荷快速增加;电网逐渐演变,负荷呈现随机性、波动性[1-3],以及负荷电流呈现大范围快速波动特征,这些特性可导致电能表电能计量失准[4-5],有时甚至会导致电能表严重超差[6]。

电能表作为电能交易的计量器具,计量准确度关系到供电方、用电方的经济利益;电能测量算法误差是影响电能表准确度的重要因素。多年来,国内外学者的研究工作集中在时域功率电能测量算法构建与算法误差分析,文献[7-8]设计了一种低通滤波器算法,测量动态场景下的有功功率与电能,误差在10-2量级内;文献[9]分析给出了稳态条件下复化矩形、复化梯形、复化辛普森电能数值积分算法电能测量误差;文献[10]分析了复化Cotes积分电能测量算法误差,文献[11]提出了复化Newton-Cotes积分电能测量算法,提高电能表的准确度,文献[12]提出了改进复化辛普森积分电能测量算法,减小电能测量算法非同步采样的误差。

近年来,国内外学者的研究集中在频域功率与电能测量算法构建与算法误差分析,并取得了大量研究成果,如:提出了基于离散傅里叶级数的谐波功率测量算法[13];提出了Hanning窗插值FFT电能测量算法[14]、Nuttall窗插值FFT电能测量算法[15]、Blackman-Nuttall窗插值FFT电能测量算法[16]、卷积窗插值FFT电能测量算法[17]、自乘窗插值FFT电能测量算法[18]、自乘-卷积窗插值FFT电能测量算法[19]。上述算法能够实现稳态条件下,基波与各次谐波功率与电能的准确测量。

目前,已提出的时域和频域功率电能测量算法,测量稳态功率信号准确度可达10-6量级,然而,近年来国内外研究结果表明,在复杂动态场景下,目前已提出的时域和频域功率电能测量算法误差显著增大[20-22],不能满足动态场景下电能准确测量的要求。近年来,本团队分析了动态场景条件下的电能测量算法误差,发现在稳态场景条件下,即使传统电能测量算法误差能够达到10-6量级,但是,在动态负荷电流大范围快速波动条件下(动态条件下),传统电能测量算法误差可以增大到10-2量级[23],传统电能测量算法出现了失准问题。到目前为止,在动态场景条件下,导致电能测量算法失准的重要影响因素尚不清楚,如何构建动态负荷电能测量算法,解决动态场景下传统有功电能测量算法失准的问题,是本领域亟待解决的难题。

文中针对传统电能测量算法失准的问题,以电能计量芯片中常采用的低通滤波器卷积和有功电能测量算法为对象,重点分析了导致有功电能测量算法失准的重要影响因素;据此,构建了动态场景下有功电能测量的两种新算法,旨在解决稳态电能测量算法失准的问题。

1 有功电能卷积和测量算法

1.1 有功功率卷积和测量算法

智能电能表电能计量系统,通过其内部有功功率与电能测量算法实现有功电能测量。设电能表电压通道输出的离散电压信号为u(n),电流通道输出的离散电流信号为i(n),电能表电压信号与电流信号相乘可得瞬时功率信号p(n):

p(n)=u(n)i(n)

(1)

电能表中采用瞬时功率信号p(n)通过低通滤波器滤波得到瞬时有功功率信号po(n),设低通滤波器的抽样响应为h(n)。低通滤波器的抽样响应h(n)与瞬时功率信号p(n)卷积得到瞬时有功功率信号po(n),则有功功率测量算法表示为:

po(n)=p(n)*h(n)=[u(n)i(n)]*h(n),n=0,1,2,…

(2)

将低通滤波器输入长度为N的电压、电流、瞬时功率信号分别映射为N维欧式空间向量U、I、P:

U=[u(0),u(1),…,u(N-1)]T

(3)

I=[i(0),i(1),…,i(N-1)]T

(4)

P=[p(0),p(1),…,p(N-1)]T=U⊙I

(5)

式中⊙表示矩阵的Hadamard积运算。

在电能表电能计量芯片中,通常采用矩形窗低通滤波器测量有功电能,矩形窗低通滤波器的抽样响应h(n)表示为:

h(n)=1/Lh

(6)

式中Lh为矩形窗低通滤波器的长度。在式(2)中,将低通滤波输出的瞬时有功功率信号po(n)表示为N+Lh-1维向量Po,代入式(3)可得有功功率卷积和测量算法。

(7)

式中H定义为低通滤波器卷积和测量矩阵,矩阵元素由低通滤波器抽样响应系数构成。

1.2 传统有功电能测量算法

根据有功电能的定义,电能测量算法累计的电能理论值为有功功率卷积和测量算法输出的瞬时有功功率信号po(n)与采样间隔Ts乘积的累加值。为了采用矩阵简洁的表示电能测量算法,文中定义了功率信号向量:

P′=[p′(0),p′(1),p′(s),…,p′(m),…,p′(n)]T

(8)

式中元素p′(s)可以表示瞬时功率信号p(s)或输出有功功率信号po(s)。定义列向量P′自元素p′(s)至p′(m)的累加和运算为:

(9)

到目前为止,在传统电能表计量芯片中,根据低通滤波器输入瞬时功率信号p(n)的有功功率P(k)判断是否满足阈值条件;P(k)大于启动功率阈值PTV时,则启动有功电能eo(n)的累加运算,否则停止电能累加运算,据此,构建传统有功电能卷积和测量算法和电能累加功率阈值约束条件:

(10)

式中k为周期序数;s.t.为功率阈值约束条件;P(k)为p(n)第k个周期的有功功率:

(11)

式中Lc为电压与电流信号每周期采样点数,其他参数同前。

1.3 改进约束条件的有功电能测量算法

针对在动态条件下传统有功电能测量算法失准问题,文中构造一种改进约束条件的有功电能测量算法,基于传统有功电能测量算法,改进了传统有功电能测量算法中有功电能累加的启动功率阈值判别方法,将启动功率阈值由滤波器输入端判别,改进为滤波器输出端判别,即根据低通滤波器输出有功功率信号po(n)判断是否满足阈值条件;当输出有功功率信号po(n)大于或等于启动功率阈值PTV时,开始电能累加运算,po(n)若小于启动功率阈值PTV,则停止电能累加运算。改进约束条件的有功电能测量算法表示如下:

(12)

式中,电能累加的时间范围N′+Lh-2,大于式(10)的时间范围,可以解决传统有功电能测量算法在电能累加过程中丢失部分电能值问题。

2 有功电能测量算法动态误差分析

2.1 OOK动态测试信号

为分析传统有功电能测量算法与改进约束条件的有功电能测量算法的动态测量误差,文中采用了正弦波形OOK动态测试信号,可反映动态负荷波动特性,其包括稳态正弦电压信号us(t)、OOK动态电流信号iOOK(t)与OOK动态功率信号pOOK(t)[24]:

(13)

(14)

(15)

其中,U、I分别为电压、电流信号有效值;f与T分别为电压、电流信号频率与周期;φm为电压与电流信号第m个周期的相位差;am取值为1或0,am取值为1表示第m个周期的电流信号状态为“导通”,am取值为0表示第m个周期的电流信号状态为“关断”;g(t-mT)为窗函数:

(16)

OOK动态测试信号的通断比为电流信号连续导通周期数与电流信号连续关断周期数之比。

2.2 传统与改进约束条件的有功电能测量算法误差

瞬时功率信号p(n)在N′点时间内的理想电能值er(n)为瞬时功率信号p(n)与采样间隔Ts乘积的累加值:

(17)

定义传统与改进约束条件的有功电能测量算法的绝对误差为算法测量得到的有功电能值eo(N′)与理想电能值er(N′)差值的绝对值:

Δe=|eo(N′)-er(N′)|

(18)

相对误差δe为:

(19)

文中算法误差仿真实验中产生的OOK动态测试信号参数均为:电压信号有效值U取归一化值1 V,电流导通信号有效值取归一化值1 A,电流关断信号有效值取0 A;电压与电流信号相位差φm为0。

仿真实验中,采用了IEC 62053-21标准中稳态测试信号与OOK动态测试信号。其中,稳态的电压与电流信号频率f取50 Hz、49.8 Hz、50.2 Hz三种情况,电压、电流信号有效值分别取归一化值1 V与1A,电压、电流信号的初始相位取0;OOK动态测试信号通断比为8∶8,OOK电压与电流信号的频率f取50 Hz、49.8 Hz、50.2 Hz。稳态测试信号与OOK动态测试信号持续时间长度为10 s,启动功率阈值设置为0.4%。文中传统有功电能测量算法,以及改进约束条件的有功电能测量算法分别采用三种长度的低通滤波器,算法相对误差如表1所示。

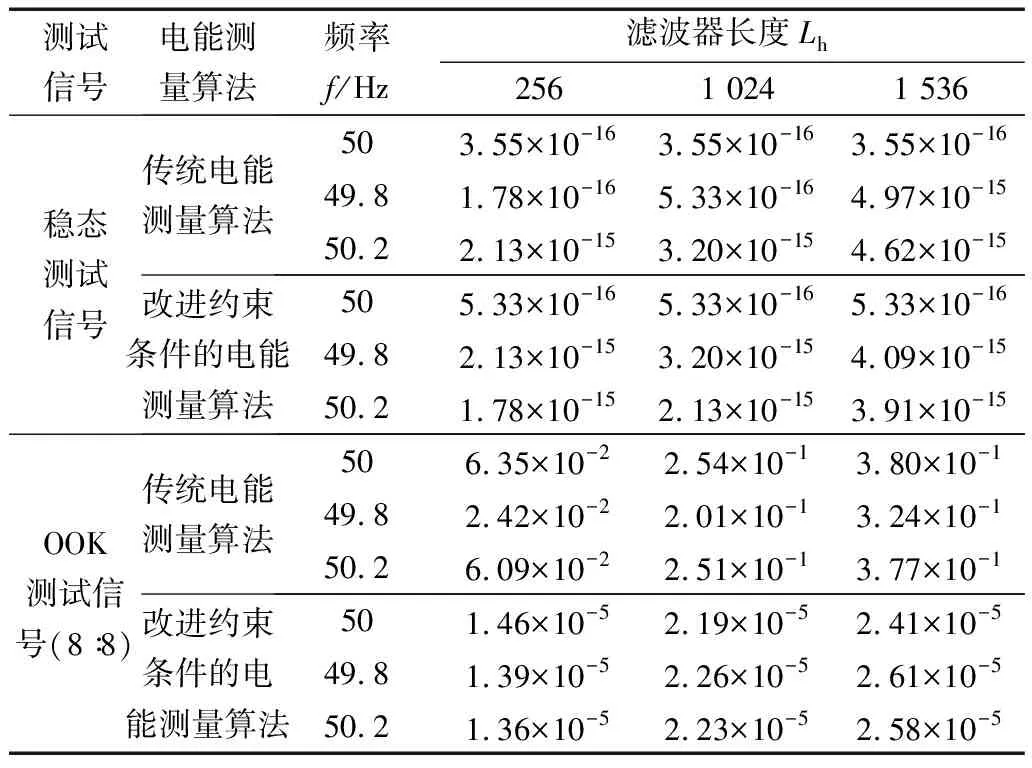
表1 传统与改进的电能测量算法误差

表1结果表明:1)传统的有功电能测量算法误差随滤波器长度Lh增加而增加。Lh为1 536时,误差达3.80×10-1,滤波器长度是影响有功电能测量算法误差的重要因素之一; 2)在动态测试信号时,改进约束条件的有功电能测量算法最大误差为2.61×10-5,优于传统有功电能测量算法误差3.80×10-1约四个数量级,解决了动态条件下,传统有功电能测量算法由于启动功率阈值导致算法失准的问题。

3 非交叠抽取动态有功电能测量算法

为进一步减小电能测量算法动态误差,文中构建了非交叠抽取动态有功电能测量算法,构建过程如下。

1)构建非交叠矩阵:取滤波器长度Lh为离散电压与电流信号一个周期采样点数Lc,每隔Lc行抽取式(7)矩阵H的子矩阵,得到矩阵H的子矩阵Hk,Hk是H的第kLc行,包含全部滤波器抽样响应系数,HR=[h(Lc-1),h(Lc-2),…,h(0)],设Nc=N/Lc,Hk的表达式为:

(20)

将子矩阵Hk按抽取顺序排列构建非交叠矩阵Hs:

(21)

(22)

对输入被测瞬时功率信号p(n)分段,分段长度取电压与电流信号每周期采样点数Lc,共分为Nc段。按照上述方式分段后,将第k段瞬时功率信号p(n)表示为Lc维向量Pk:

(23)

(24)

则瞬时功率信号p(n)第k个周期的有功功率测量值为:

(25)

3)有功电能算法:式(25)给出了被测瞬时功率信号的分段与段内点积算法,可求得每周期段的有功功率。求Lc时间点内(p(n)第k个周期)累计的有功电能为:

(26)

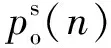
(27)

式(25)～式(27)给出了非交叠抽取动态有功电能测量算法,式(25)中滤波器系数选取了矩形窗滤波器系数。

4 非交叠抽取动态有功电能测量算法误差

仿真实验中取矩形窗低通滤波器长度为1 536,启动功率阈值为0.4%;采用持续时间长度为10 s,通断比为8∶8、9∶6、12∶7的三种OOK动态测试信号,分析比较传统有功电能测量算法、改进约束条件的有功电能测量算法与非交叠抽取有功电能测量算法的相对误差。基于以上实验条件,三种OOK电压与电流测试信号频率f条件下电能测量算法误差的仿真结果如表2所示。

表2 电能测量算法误差

表2结果表明:1)传统有功电能测量算法与改进约束条件的有功电能测量算法误差受频率变化影响较小;2)非交叠抽取有功电能测量算法误差为1.94×10-4,优于传统有功电能测量算法误差3.80×10-1约三个数量级,文中提出的两种算法误差显著优于传统有功电能测量算法;3)动态负荷8:8通断比波动速度下,传统有功电能测量算法误差由稳态测试信号10-15量级增大至10-1量级,动态负荷波动速度是导致算法失准的重要因素之二。

5 结束语

文中针对传统低通滤波器卷积和有功电能测量算法,在动态场景下电能测量失准的问题,构建了低通滤波器卷积和测量矩阵,表示滤波器输入瞬时功率与输出有功功率的关系,提出了两种有功电能测量新算法,采用滤波器长度变化、信号频率变化、电流波动速度变化多种仿真算例,分析了传统算法与新算法的误差性能,给出如下结论:

1)构建了传统有功电能测量算法矩阵形式与电能累加功率阈值约束条件,通过多种条件下的仿真实验,发现了滤波器长度与动态负荷波动速度是导致算法失准的两个重要因素;

2)提出了一种改进约束条件的有功电能测量新算法,在滤波器输出端实现启动功率阈值的判别,新算法的误差2.61×10-5比传统有功电能测量算法的误差3.80×10-1提高了约四个数量级;

3)提出了一种非交叠抽取动态有功电能测量新算法,采用非交叠抽取测量矩阵的方式,构建了非交叠矩阵,在滤波器输出端实现启动功率阈值的判别,在动态负荷快速波动下,新算法误差为1.94×10-4,比传统有功电能测量误差3.80×10-1提高了约三个数量级。

在目前新型电力系统中电网负荷复杂动态变化的场景下,本文提出的两种电能测量新算法可为改进电能表的动态误差性能提供有效的技术手段,较好解决了动态场景下传统有功电能测量算法失准的问题。