考虑市场交易的新型电力系统调度辅助决策方法研究

吴任博,刘淑琴

(山东大学 电气工程学院,济南 250000)

0 引 言

随着当今电力控制和通信能力的提高,以及多样化的需求侧技术出现,用更灵活的新型电力系统取代现有的电力系统成为可能[1]。提高系统控制准确性的一个挑战是在电力市场出清机制中整合负荷管理计划和主动配电网技术,以反映市场结果对新兴技术的影响和依赖[2]。在目前方法中,实体电网及其组件(例如,储能设备)的实际动态在很大程度上被忽略。这种简化在极大系统的情况下是可接受的,以达到较优的解决方案,但对于其他情况可能会产生不可行结果[3]。事实上,每个智能电网的决策过程都是一个复杂的优化问题,既有连续决策,也有离散决策。当独立的智能电网融入电力市场运行并与之互动时,如何解析地确定独立智能电网的运行策略,基本上是个未知数[4]。因此,考虑到这些关键因素和相互作用,必然需要一种有效的能源管理方法来支持电力市场中智能电网的最优调度和运行计划。

为了应对现代电力市场中智能电网的运行挑战,学者开发了许多辅助决策模型和求解方法。在文献[5]中,提出了一个的两层模型来确定电力市场中负荷削减和灵活负荷(即需求响应组合)的最优调度。在文献[6]中提出了Stackelberg博弈模型来研究电网运营商和配备了需求响应用户之间的交互作用。文献[7]建立了电力供给方和终端用户之间的Stackelberg博弈,其中供给方充当追逐利润的领导者,而终端用户充当福利最大化的追随者。文献[8]提出了智能电网零售商作为能源市场和终端用户之间的中介机构的能源定价和调度的双层优化模型。文献[9]中引入了一个随机双层模型,在该模型中,上层的电网运营商最小化总的运营成本,而下层的需求响应聚合体最大化利润。上述文献将智能电网建模为受控或价格接受者,在电力市场内由电网运营商作为综合负荷或电源运营管理。这些假设在很大程度上是不切实际的,因为考虑如储能、光伏等分布式能源,基本上是私有的,几乎没有可能让电网运营商全权管理或运营。

在最近的一些工作中,考虑了部分电网的决策独立性。在文献[10]中讨论了一组主动配电网和输电系统之间的能量管理问题。文献[11]提出了一个框架和迭代算法来协调输电网和多个微电网,以找到这些独立系统的最佳运行点。文献[12]考虑了由引导者和跟随者组成的多子网系统的分散结构,并通过双层优化来解决能量管理问题。单个子网在最坏情况下进行多阶段稳健优化以最小化运行成本,而在系统层面(即上层),通过最小化日常运行成本来进行能量管理。然而这些工作忽略了电力市场及其与多子网组成的新型电力系统的相互作用。

文献调研显示,与丰富的智能电网运行和优化研究文献相比,考虑智能电网自主性和市场运行的模型研究较少。事实上,主动配电网是一个关键组件,它将该地区的各种可再生资源、储能设备和响应负载互联在一起,以满足用户的电力需求。因此,应该采用一种考虑所有这些因素和相互作用的分析方法来确定电网的实际运行策略。因此,文中开发了一个基于市场的框架来研究电力市场和包含多个主动配电网的新型电力系统的相互作用,并进行辅助决策。在所提出的方法中,子电网预测市场价格,并可以相应地影响市场数量。也就是说,其参与市场博弈,这种互动通过双层优化来建模。顶层的市场运营商对日前市场进行出清,而较低层的多个独立子电网按顺序行动,以确定其最优调度。在这里,每个子电网都是一个自组织系统,其运行和管理自己的网络,以利用该地区各种相互连接的可再生资源、储能设备和响应能力较强的负载。在市场方面,假设运营商收集报价,并使用机组组合问题结算日前市场。使用二阶圆锥交流潮流方法来求解运营商优化问题,以考虑输电系统的电压和无功约束。

将子电网的物理特性建模为这种类型的双层优化产生的最大困难是下层问题决策的离散特征。这是一个巨大的计算挑战,目前大多数可用的求解技术主要依赖于缺乏计算效率并可能导致次最优的启发式、近似或简化建模方法。与现有方法不同,本文扩展了文献[13]中的重构和分解方案,以求解双层优化问题。

1 优化建模

在这一部分中,给出了考虑独立子电网最优运行的双层优化方案,考虑了混合整数规划、二次规划和线性规划。

1.1 模型符号

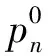
1.2 建模假设

图1描述了所提出的双层优化模型的结构。上层优化给出常规发电机组的启动、关闭和调度决策,最小化系统总成本。下层优化对应着每个子电网内部能耗优化,给出负荷管理、储能充放电等具体决策。假设发电机组向市场运营商提交报价,这些报价体现了其实际运营成本和约束[14]。文中,运营成本包括可变(运行)成本、启动成本、关闭成本和空载成本。运行约束包括爬坡率、最小正常运行时间和停机时间以及最小和最大发电量。一旦收集到报价,就决定机组的启动和关闭。

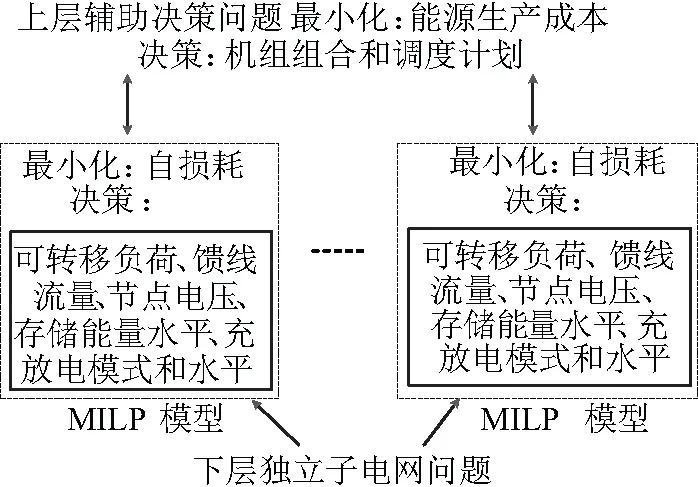
图1 辅助决策模型架构

1.3 双层优化模型

如前所述,市场运营商收到来自发电部门的报价,其中包括运营成本数据和运营限制。然后执行多阶段优化,以出清日前市场。这是上层优化,其解决方案得出了常规发电机组的启动、关闭和调度决策。将与输电系统相连的子电网的需求视为因变量,由下层优化迭代确定。

利用二阶二次交流潮流模型,上层优化问题可写成:

(1)

s.t.

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

vit-vit-1=uit-sit,uit,sit∈{0,1} ∀i∈Δ,t∈T

(14)

(15)

(16)

(17)

Cijt=Cjit,Sij=-Sjj,Cijt≥0 ∀ij∈Ω,t∈T

(18)

(19)

(20)

(21)

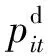
假设系统内存在一些独立的子电网,它们通过变电站连接到输电系统,并与主电网交换电力。

每个子电网的运营商预测市场价格(在连接节点),并通过使用混合整数线性规划最小化其实际和无功消耗来计算最优运行决策。在子电网优化问题中,考虑了配网的技术约束以及各种需求侧技术(储能、需求响应等)。因此,对每个输电节点i处的子电网都求解以下最优潮流问题:

(22)

∀n∈Φi,t∈T

(23)

∀n∈Φi,t∈T

(24)

Unt=Umt-2(rmnpmnt+xmnqmnt) ∀n∈Φi,m∈Φi(n),nm∈Ni,t∈T

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

(35)

znt∈{0,1} ∀n∈Φi,t∈T

(36)

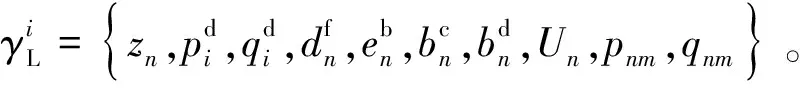
由此可见,下层优化问题本质上是一个混合整数线性规划。各子电网运营商通过求解该模型来计算最优自耗量及其调度决策。采用KKT条件或强对偶性的传统重述方法,以等价的对应问题取代下层优化问题,在此背景下并不适用。在下文中,提出了一种重构和分解方法来计算该问题。

2 求解方法

优化模型式(1)、式(22)由一个混合整数二阶锥规划的上层优化和多个混合整数线性规划(Mixed Integer Linear Programming,MILP)下层优化问题组成。为了计算这个双层问题,使用并扩展了文献[13]中提出的重构-分解算法,该算法将原始模型划分为一个主问题和多个子问题。

为了使本节中的论述更易理解,首先给出双层优化问题式(1)、(22)基于矩阵的表示法,如下所示:

minax+by

(37)

s.t.

By+Cri=d

(38)

Ax+Dy≥l,x∈{0,1}

(39)

‖Hy‖≤hy

(40)

其中:

ri∈argmin{ei(ri+yi):

(41)

s.t.

Giwi+Eiri+Oiyi=fi

(42)

Fiwi+Kiri≤ki

(43)

ri≥0,wi∈{0,1}}∀i∈Δ

(44)

其中x和y表示上层优化二进制和连续变量,ri和wi表示与输电节点i处的子电网相关联的下层优化的连续和二进制变量。使用适当维度的系数矩阵或向量(A,a,B,b,Ei,ei,l,D,d,Fi,fi,Gi,H,h,Ki,ki,Oi)使这些变量相关联。在约束式(40)中,使用符号‖·‖表示向量(矩阵)的l2范数。方程式(41)表示目标函数,式(42)～式(44)表示与输电节点i处的每个子电网相关联的下层优化问题的原始约束。

为了给算法提供可分解的结构,遵循文献[13]中通过复制上层问题中的下层变量和约束并增加一个额外的约束式(49)来重新制定双层优化问题式(37),如下所示:

minax+by

(45)

s.t.

式(38)～式(40)

(46)

(47)

(48)

(49)

s.t.

Giwi+Eiri+Oiyi=fi,Fiwi+Kiri≤ki

(50)

ri≥0,wi∈{0,1}}∀i∈Δ

(51)

(52)

s.t.

(53)

(54)

(55)

2.1 子问题

对于给定的上层决策(x*,y*),以及连接到输电节点i∈Δ的每个子电网,计算以下子问题SP1i:

(56)

s.t.

(57)

Fiwi+Kiri≤ki:μi

(58)

ri≥0,wi∈W

(59)

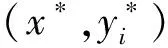
SP2:Ψ(x*,y*)=minax+by

(60)

s.t.

式(57)～式(59)

(61)

(62)

SP2是一个容易计算的MILP问题。

2.2 主问题

1)步骤1:设置LB=0、UB=∞、τ=0。

2)步骤2:求解以下主问题:

MP:Γ=minax+by

(63)

s.t.

式(38)～式(40),式(47)～式(48)

(64)

(65)

(66)

(67)

(68)

报告最优解(x*,y*)并更新LB=Γ。

5)步骤5:如果UB-LB≤,则停止求解UB。否则,τ=τ+1并返回步骤2。

该算法动态地提供上界(从子问题)和下界(从主问题),并在每次迭代中向主问题添加新的变量和约束,直到界之间的差异不大于最优性容差。

虽然主问题在每次迭代中都会随着维度的增加而变得繁琐,但该算法的关键优势在于它可以在很少的迭代次数和算法操作中产生最优解。在案例研究中,在大多数情况下,算法在3次迭代后可得出最优解,最多只需要4次迭代。

3 仿真分析

3.1 示例系统

考虑一个六节点输电网络,有四台发电机组和两个子电网,标记为SG1和SG2,其余测试参数见文献[15]。子电网分别连接到节点2和节点4,如图2所示。每个子电网有一个光伏发电和一个储能设备连接到同一节点。在24小时的时间范围内,考虑了以下案例条件:

图2 示例系统单线图

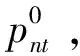
2)改变光伏-储能的位置,并且重置条件与案例1相同;

3)假定储能的充放电次数不受限制,其余条件与案例1相同;

4)每个节点处的可转移需求增加到15%,其余条件与案例1相同;

5)与案例4类似,不同之处在于50%的子电网节点具有可转移的需求,其余节点的需求是固定的。随机选择具有可转移需求的节点;

6)子电网的拓扑结构发生了变化。在子电网1中,线路2、3和5上的开关断开,线路6、7和8上的开关闭合。此外,在子电网2中,线路4、5和8上的开关断开,线路10、11和12上的开关闭合;

7)没有建模子电网,负荷产生条件类似于案例3。这种情况基本上代表了一个聚合的智能电网模型。

表1 优化示例系统辅助决策结果

图3 案例1和案例3的测试结果:SOE、节点边际电价和输电网的电压曲线

为了探讨可转移需求对子电网和主电网的影响,对于案例1和案例4,在图4中描绘了这些网络的损耗和机组组合成本。在案例4中,通过将需求响应(可转移)增加5%,在大多数时间内降低了网络损耗和成本。图5给出了输入到子电网2的有功和无功功率以及案例4和5的输电网络的平均节点边际电价。如前所述,在案例5中,只有50%的子电网节点具有可转移需求,因此,在大多数时间内,子电网的功率输入增加,这提高了输电网络的边际电价。这个实验清楚地说明了主动配电网中响应性需求的位置如何对市场结果产生显著影响。在案例6中,假设每个子电网的运营商可以更改电网配置。在此观察了这些行为对市场结果的影响。例如,与案例1相比,案例6的平均边际电价增加了7%。在案例7中,不对子电网进行建模,因此使用聚合负荷生成模型。从表1可以看出,在这种情况下,输电损耗增加,子电网的高峰需求减少。因此,与子电网建模的案例3和5相比,发电的机组组合成本却降低了。为了更好地说明,图6中描绘了在案例3和7中的输电系统的平均节点边际电价和损耗。观察到案例3出现平均边际电价的急剧增加和某些小时的损失,在案例7由于过于简化而基本上消除了这些情况。

图4 案例1和案例4的测试结果:损失和单位生产成本

图6 案例3和案例7的测试结果:平均边际电价和输电网络损耗

最后,图7显示了在本节研究的情况下,发电机的每小时投入状态(标记为Gi,i=1,...,4)和储能设备的充电/放电模式(标记为SGi,i=1,2),白色方块表示投入或充电状态,黑色方块表示退出或放电状态。它简单地展示了下层优化问题(即子电网)的负荷生成条件或建模细节的变化如何影响上层问题中的机组组合时间表。

图7 系统设备的每小时开/关状态和储能设备的充放电运行模式

3.2 30节点系统测试

将输电系统改为30节点系统[16]。并使用4节点、18节点、22节点和33节点四种子电网。它们分别连接到20、18、30和15输电节点。测试参数取自文献[15]。这些子电网分别有2、3、4、5个光伏-储能系统。在24小时内,研究了以下案例:

1)假设10%的节点需求是可转移的。对子电网中的所有储能设备施加有限数量的充电/放电次数。

2)与案例1一样,改变了原有的网络拓扑,保留了光伏-储能位置。与原有的网络拓扑相比,在子电网1中,线路2和3上的开关是断开的。在子电网2中,线路8、12、13和17上的开关断开。在子电网3中,线路3、8、11和15上的开关断开。在子电网4中,线路7、9、14、32和37上的开关断开。

3)随机改变光伏-储能的位置,并且重置条件与案例1相同。

优化结果如表2所示。观察到由于光伏-储能位置或子电网配置的变化而导致市场结果和子电网调度决策的变化。例如,与案例2相比,案例1和案例3对子电网的目标更高。此外,案例2的拓扑变化降低了子电网损耗和上层问题的社会成本。因此,从表2中的输电系统指标可以看出,输电层面的子电网简化聚合模型将低估市场运行成本,并得出不准确的结果。

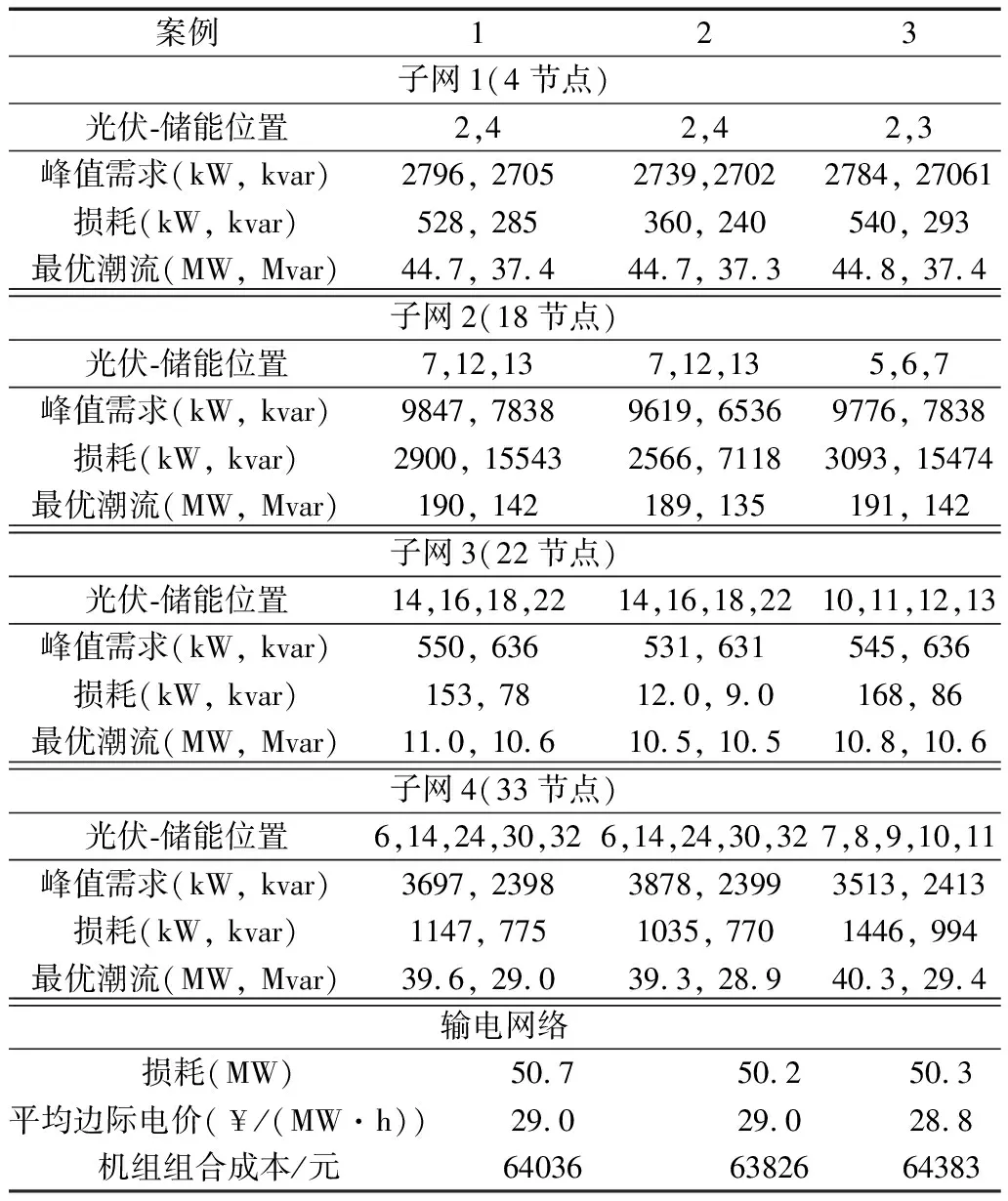
表2 优化后30节点系统辅助决策结果

3.3 57节点系统测试

将该方法应用于57节点系统[17]。该系统由7台发电机和80条线路组成。文中假设有四个子电网连接到该系统。子电网包括节点3处的13节点系统、节点9处的18节点系统、节点52处的22节点系统以及节点42处的33节点系统。

表3给出了三种情况下的优化结果。这些情况与上述30节点系统中的情况类似。在案例1中,假设10%的节点需求是可移动的,并且储能设备的充放电次数有限。在案例2中,光伏-储能位置改变,其余条件与案例1相同。在案例3中,修改子电网拓扑,其余条件类似于案例1。

表3 优化后57节点系统辅助决策结果

从表3可以看出,子电网的最优决策的变化反映在市场结果中。例如,当子电网中的光伏-储能位置与案例2相同时,输电损耗和社会成本达到最低值。这表明实际市场结果取决于子电网的反应和运行决策,以及在对这些系统建模时考虑的物理细节水平。

4 结束语

本文提出了一种在日前市场运行中集成自治子电网辅助决策问题的建模框架。制定了一个双层优化方法来分析市场运营商与包含分布式能源以及需求侧技术的独立子电网之间的相互作用。上层优化问题使用二阶二次交流潮流模型来描述日前市场的出清过程。下层问题优化了自治子电网的能耗管理,其中考虑了与储能设备和可转移需求有关的决策的混合整数性质。考虑到上层问题和下层问题的混合整数结构,提出了一种重构分解方法,使用一个主问题和多个子问题迭代地求解优化模型。在三个测试系统上对所提出的方法进行了评估,观察到子电网的聚合建模方法使用了配电系统的简化模型并忽略了储能设备的实际特性,将导致产生不准确的结果。所提出的方法通过捕获物理输配电系统、下层决策过程的离散性以及电力市场和子电网之间的相互作用来提高求解精度。

未来研究的可能方向包括纳入需求侧技术的更多特征,如需求响应的反应时间、电动汽车等,并评估它们对市场运行的影响。