含高比例分布式光伏的配电网多目标概率规划方法

惠慧,李蕊,朱逸镝,张育炜,李天翔,陆文标,肖迁

(1.中国电力科学研究院有限公司,北京 100192; 2.天津大学 未来技术学院,天津 300072;3.天津大学 电气自动化与信息工程学院,天津 300072)

0 引 言

在全球气候变化和环境污染问题加剧的背景下,推动可再生能源的发展已变得至关重要[1]。分布式光伏具有配置灵活、用地面积小等优点,且邻近负荷中心利于消纳[2],近年来,其在新型配电网中的接入比例迅速增长[3]。然而,分布式光伏出力受天气、季节等因素影响,具有不确定性,使配电网的规划运行面临严峻挑战。传统配电网规划(如多场景规划等)通常将不确定性规划模型转化为等价的确定性规划模型[4],模型的精度难以保证,且对于不确定性因素的考虑不够全面。因此,亟需开展考虑分布式光伏不确定性的配电网概率规划研究。现有配电网分布式光伏规划方面研究主要体现在两个方面:一为考虑配电网运营投资成本的经济性规划[5],二为考虑高比例分布式光伏接入造成运行指标劣化的可靠性规划[6]。

在经济性规划方面[7-11],分布式光伏的大规模接入使得配电网的规划成本大幅上升,为提升配电网规划运行经济效益,有诸多研究提出规划成本优化方法。文献[7]从不同主体的利益角度出发,针对配电网扩展规划问题,建立基于主从博弈的双层优化模型。文献[8]通过主成分-高斯混合聚类算法对数据进行场景降维,以总成本最小为目标构建规划模型,为配电网规划提供典型场景生成方法。文献[9]提出一种考虑综合能源系统设备和配电网变电站容量协同规划的多场景规划方法,实现了投资成本与运行成本的协同优化。文献[10]基于全寿命周期成本管理对配电网发展规划方案进行优化。文献[11]提出一种考虑源网荷协同的配电网分布式光伏储能多目标优化配置方法,提高了优化配置方案的经济性,实现了源网荷协同规划。然而,上述文献大多并未考虑光伏渗透率的提升和运行指标的优化。

在可靠性规划方面,随着分布式光伏接入比例的提升,其无序接入造成了配电网电压的剧烈波动与网损的急剧攀升,为使高比例分布式光伏接入后的配电网能够安全稳定运行,需对分布式光伏进行合理配置[12-17]。文献[12]提出一种风-光-储两阶段规划配置方法,考虑有功网损灵敏度和系统电压稳定指标最大等建立多目标规划模型,实现了配电网运行情况的改善。文献[13]引入遗传算法对PSO算法进行改进,兼顾电压越限风险的降低与光伏渗透率的提升。文献[14]考虑经济性、环保性、安全性等指标,对分布式能源进行优化配置,为多指标评价的配电网规划奠定基础。文献[15]基于信息熵的场景提取方法,建立多场景光伏及储能选址定容规划模型,实现配电网运行的经济性与可靠性提升。文献[16]利用聚类分析确定规划场景,基于多种群牵引差分进化算法,实现全年网损与电压偏差最小的优化规划。文献[17]基于节点脆弱性评估对配电网分布式光伏进行优化配置,改善了配电网的节点电压与网损情况。上述文献考虑了高比例分布式光伏接入后造成的可靠性问题,但仍基于确定性出力场景进行规划,对分布式光伏不确定性的考虑不够全面,所得结果与实际运行情况不匹配。

为提升分布式光伏不确定性场景下的配电网运行稳定性,降低配电网经济成本,文章提出一种含高比例分布式光伏的配电网多目标概率规划方法。首先,基于光伏出力数据,采用K-means聚类与概率潮流生成光伏不确定性场景,模拟分布式光伏实际运行情况;在此基础上,计及建设成本、光伏渗透率、概率潮流下的电压偏差指数等指标建立双层概率规划模型,引入概率潮流表征光伏出力对系统的影响,从而提升配电网对不确定性光伏出力的适应能力;最后,采用安徽某地光伏出力作为典型数据,以IEEE 33节点系统为算例开展了多场景算例分析。

1 含高比例分布式光伏的配电网不确定性场景构建

为实现考虑光伏不确定性的配电网概率规划,需对分布式光伏实际运行情况进行模拟,文章基于K-means聚类、概率潮流等方法,提出含高比例分布式光伏的配电网不确定性场景构建方法。

1.1 光伏出力概率模型

光伏发电系统输出功率受到天气、季节等因素的影响,具有不确定性。研究表明,Beta分布对光照强度的拟合效果较好[18],其概率密度函数的表达式可以通过光照强度的平均值和标准差近似计算得到,表达式如下:

(1)

(2)

式中r和rmax分别为实际光照强度和最大光照强度;α和β为形状参数;μr和σr分别为光照强度的平均值和标准差。

光伏出力与光照强度之间满足线性关系,因此光伏出力同样服从Beta分布,其概率密度函数为[19]:

(3)

式中PPVG为分布式光伏机组的输出功率,PPVG=rAη,其中r为光照强度,A为电池等效面积,η为光电转换效率;PPVG,max为分布式光伏机组的最大输出功率。

1.2 不确定性光伏出力场景生成

1.2.1 数据预处理

由于实际的光伏数据中存在超出正常日照时间范围、量级有明显差异等不符合实际的错误数据,因此有必要对光伏数据进行预处理,以提高数据的可用性和准确性。

文章数据预处理包括异常值处理和数据转换两个步骤。具体如下:

1)异常值处理:首先通过经验判断结合统计方法辨识数据中的异常值,对不同季节日出、日落时段前后的数据进行辨识;其次,通过数据对比筛选出数据库中不符合实际的数据;最后,采用删除异常值方法移除数据集中的异常值,并对缺失的数据根据辨识结果采取插值处理,将日落时间段缺失数据置零,日出时间段缺失数据替换为邻近值;

2)数据转换:首先,将采集数据输入数据库并统一数值格式;其次,将不同时间尺度的连续出力数据转换为1 h时间尺度的出力数据集;最后,判断数据集规模并转换为相应的日出力数据集。

1.2.2K-means聚类方法

由于实际的光伏出力场景数据量较为庞大,基于全部场景数据进行概率模型建模计算效率较低,需要对其进行场景削减。文章采用K-means聚类方法进行场景削减,该算法基于相似性原则,旨在确保同一类的光伏出力数据点高度相似,而与其他类的光伏出力数据点有明显差异[20]。具体步骤如下:

1)随机选取样本中的k个点作为质心;

2)分别计算其他样本到初始质心的距离,将样本分类到与之距离最近的质心类别,样本距离表达式为:

(4)

式中xi和yi分别为每个样本在空间中的坐标;

3)对每个类别求平均值,求解出新的聚类质心;

4)与前一次计算得到的k个聚类质心比较,若聚类质心发生变化,转步骤2),否则转步骤5);

5)当质心不再变化时,停止并输出聚类结果。

1.2.3 最佳聚类数目确定

在K-means算法中,簇的个数(即聚类数目)k是影响聚类结果的重要因素,需要人为输入进行确定。若k的取值过大则聚类失去意义,若取值过小则聚类特征不够显著。肘部法是确定k值的一种常见方法[20],具有直观、高效的特点,同时无需复杂的数学计算或算法,所需计算资源少,适合处理光伏出力数据等大规模数值型数据,故文章采用此方法确定最佳聚类数目。

肘部法利用不同k值及其对应的误差平方和(sum square error,SSE)评价聚类效果。SSE值越小表示每一类数据相似程度越高,聚类效果越好,计算公式为:

(5)

式中Ci代表第i个簇;p为簇Ci里的样本点;mi为簇的质心。

通常SSE值随着k值增大而减小,其对应图像存在下降拐点,在拐点处增加k值所带来的聚类效果提升相对较小。由于k值不宜过大,所以SSE下降拐点对应的k值为最佳聚类数[20]。

1.3 概率潮流计算

概率潮流计算是一种计及光伏出力等不确定性因素,并表征其对系统影响的潮流计算方法[21]。相比传统的潮流计算方法,概率潮流计算考虑到光伏出力的概率特性,所得结果更符合含分布式光伏配电网实际运行情况[22],为所提概率规划模型提供了数据基础。

概率潮流算法包含模拟法、近似法和解析法,其中,蒙特卡洛模拟法因具有高计算精度的优势[22],文章采用蒙特卡洛模拟法求解概率潮流问题。

蒙特卡洛模拟法是一种基于随机抽样的数值计算方法[23],通过在随机变量的可能分布中进行随机抽样,模拟出大量可能的系统运行状态,其步骤如下:

在包含m个单元的系统中,Xi=(X1,X2,…Xm)代表每个子单元的状态变量向量,xi=(x1,x2,…xm)为该向量的数学表达式。当这些单元相互独立时,其联合概率分布P(X)为:

(6)

理论上,对所有样本抽样后可以根据其联合概率分布计算期望值和方差,然而,由于实际采集样本数量的限制,期望值和方差通常为估计值:

(7)

(8)

式中E(F)为实验函数的期望;V(F)为实验函数的方差;Ns为样本数量;Fi(X)为第i次采样中获得的实验函数。

蒙特卡洛概率潮流计算包括确定计算参数、进行蒙特卡洛模拟、进行潮流计算和统计概率分布等步骤,具体如下:

1)确定计算参数。包括发电机出力上下限、节点负荷、分布式光伏概率分布等参数;

2)进行蒙特卡洛模拟,生成概率样本。通过随机抽取分布式光伏出力的概率样本,得到不同概率场景;

3)对于每个概率样本,进行潮流计算。根据样本中的负荷消耗和分布式光伏出力,计算电力系统中各节点的电压和功率;

4)统计各节点的电压和功率的概率分布。根据蒙特卡洛模拟的结果,得到配电网中各节点电压和网损的概率密度函数(probability density function,PDF)及累积分布函数(cumulative distribution function,CDF)。PDF与CDF将满足以下关系:

(9)

式中X为状态变量,文章中指节点电压及网损;FX(x)为状态变量X的CDF;fX(x)为状态变量X的PDF。

2 含高比例分布式光伏配电网双层概率规划模型

在分布式光伏的出力波动影响下,配电网的规划成本攀升,运行稳定性降低。为实现含高比例分布式光伏配电网的经济可靠规划,文章基于前述不确定性场景,建立含高比例分布式光伏配电网双层概率规划模型。

含高比例分布式光伏配电网双层概率规划关系如图1所示。

图1 双层概率规划关系图

其中,模型上层为规划层,以投资建设成本最小和光伏渗透率最大为目标,确定光伏、储能的选址与容量配置方案;下层为运行层,考虑分布式光伏出力的不确定性,量化光伏出力、系统网损和电压产生的随机波动,以概率潮流下的运维成本、网损成本、购电成本和电压偏差指数最小为目标,优化分布式光伏出力以及储能各时段充放电功率。运行过程中,上层将分布式光伏与储能配置方案传递给下层,作为下层的初始条件,下层基于上层的结果对分布式光伏与储能进行运行优化,并将运行优化结果传递给上层。

2.1 规划层模型

2.1.1 目标函数

由于投资成本和光伏渗透率量纲不同,需要进行归一化后建立目标函数。

y=(x-xmin)/(xmax-xmin)

(10)

式中x为目标函数值;xmax和xmin分别为目标函数的最大值和最小值;y为归一化后的目标函数值。

F1=min{C′T-η′}

(11)

式中C′T为归一化的投资成本;η′为归一化的光伏渗透率。

1)投资成本。

(12)

式中r为贴现率;n为分布式光伏和储能设备的使用年限;cPV为单位容量分布式光伏投资成本;cESS为单位容量储能投资成本;PPV为分布式光伏总装机容量;PESS为储能总装机容量。

2)光伏渗透率。

(13)

2.1.2 约束条件

1)分布式光伏接入节点数量限制。

(14)

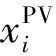
2)储能接入节点数量限制。

(15)

3)潮流约束。

(16)

式中Pi为节点i的有功功率;Qi为节点i的无功功率;Ui和Uj分别为节点i,j处的电压;Gij和Bij分别为支路ij的电导和电纳;θij为节点i,j的相角差;N为节点总数。

4)节点电压约束。

(17)

5)支路功率约束。

(18)

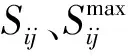
2.2 运行层模型

2.2.1 目标函数

与规划层类似,由于目标函数量纲不同,因此同样需要对其进行归一化处理。

F2=min{C′y+C′loss+C′buy+VDI′}

(19)

式中C′y为归一化的运维成本;C′loss为归一化的网损成本;C′buy为归一化的购电成本;VDI′为归一化的电压偏移指数。

1)运维成本。

(20)

2)网损成本。

网损成本表征电能传输过程中产生的有功损耗费用,用于衡量配电网的能源利用效率与经济性。

(21)

式中closs为单位网损成本;Nl为线路总数;Il,t为概率潮流所得第l条线路第t时刻的电流;Rl为第l条线路电阻。

3)购电成本。

(22)

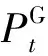
4)电压偏移指数。

电压偏移指数表征某一时间断面下,配电网中节点电压的实际值偏离额定值的程度,用于衡量配电网的电压稳定性。电压偏移指数越大,电压稳定性越差。

(23)

式中Ui,t为概率潮流所得t时刻节点i电压实际值;Ui,N为t时刻节点i电压额定值。

2.2.2 约束条件

1)潮流约束。

(24)

式中Pi为节点i的有功功率;Qi为节点i的无功功率;Ui和Uj分别为节点i,j处的电压;Gij和Bij分别为支路ij的电导和电纳;θij为节点i,j的相角差;N为节点总数。

2)节点电压约束。

(25)

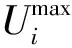
3)支路功率约束。

(26)

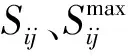
4)分布式光伏出力约束。

(27)

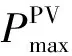
5)储能充放电功率约束。

(28)

(29)

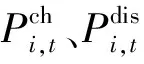
6)储能SOC上下限约束。

SOCmin≤SOCi,t≤SOCmax

(30)

式中SOCi,t为第i台储能第t时段的荷电状态(state of charge,SOC);SOCmax和SOCmin分别为储能SOC上下限。

3 模型求解

3.1 求解算法

上文所提概率规划模型为混合整数非线性规划问题,采用传统解析方法求解难度较大,因此文章采用改进的PSO算法求解所提模型。

PSO算法将优化问题的解视为粒子在空间中的位置[24],通过粒子个体之间的协作和竞争,在复杂的搜索空间中找到最优解,具体步骤如下:

1)初始化粒子群,根据设定参数生成初始化的粒子并随机生成每个粒子的位置和速度;

2)迭代更新粒子群,每个粒子根据当前速度、位置、个体最优解和群体最优解,更新速度和位置,在这个过程中,粒子不断在空间中搜索适应度更优的位置,并得到当前最优解;

3)判断是否达到终止条件,若满足终止条件,则输出粒子群中最佳的粒子位置和对应的最佳适应度作为优化问题的解和目标函数的最小值;否则转步骤2)。

在PSO算法中,惯性权重ω对算法的寻优性能有较大影响。较大的ω有利于增强全局搜索能力;较小的ω则有利于增强局部搜索能力[25]。为提升PSO算法收敛能力,本文采用线性下降惯性权重的改进方法:

(31)

式中tmax为最大迭代次数;ωmax和ωmin分别为ω的上下限,文章设为0.9和0.4。

计算过程中,ω将随着迭代次数的增加而逐渐减小。计算初期算法具有较强的全局搜索能力,避免较早的收敛于局部最优;计算后期算法具有较强的局部搜索能力,从而提高算法的寻优性能。

3.2 求解步骤

文章所述双层概率规划模型求解流程如图2所示,具体步骤如下:

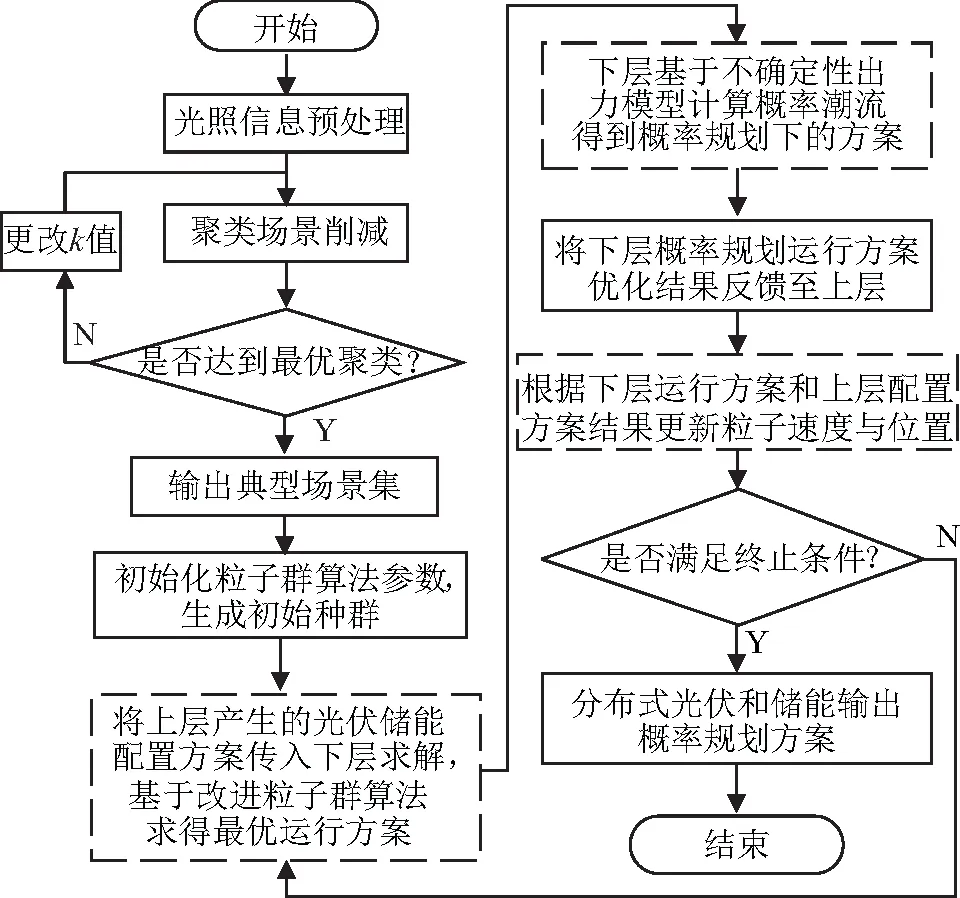
图2 概率规划求解流程图

1)对光照信息进行预处理,根据肘部法确定最优聚类数目,并基于K-means聚类方法对光伏出力数据进行场景削减,生成有代表性的光伏出力概率场景集;

2)初始化粒子群算法参数,生成初始种群;

3)将上层产生的光伏、储能配置方案传递给下层,作为下层的初始条件,下层模型计算多次概率潮流量化光伏出力、系统网损和电压产生的随机波动,从而确定每个时段系统运行的最优策略;

4)将下层产生的最优运行方案传递给上层,上层模型基于下层优化过后的运行方案指标值更新全局粒子速度与位置;

5)判断是否满足终止条件。若满足,则全局最优粒子的位置即为分布式光伏和储能最优配置方案;若不满足,则更新粒子的位置和速度,转至步骤3)。

4 算例分析

4.1 算例说明

为验证文章所提方法的有效性,选取IEEE 33节点算例进行仿真分析。其中,IEEE 33配电网拓扑如图3所示。

图3 IEEE 33节点配电网拓扑图

配电网日内负荷分布情况如图4所示,由图4的节点负荷功率分布可见,负荷功率于节点24～33之间达到高峰,其次是节点7～14之间,而其他节点负荷功率相对较低,由此可得,负荷主要集中于以上两个节点区间;分布式光伏和储能的使用年限设置为10年,光伏渗透率最高不超过70%;基于安徽某地实际光伏数据生成光伏不确定性场景,并利用肘部法确定k=4时聚类效果最佳,所得典型场景出力如图5所示。

图4 日内负荷分布情况

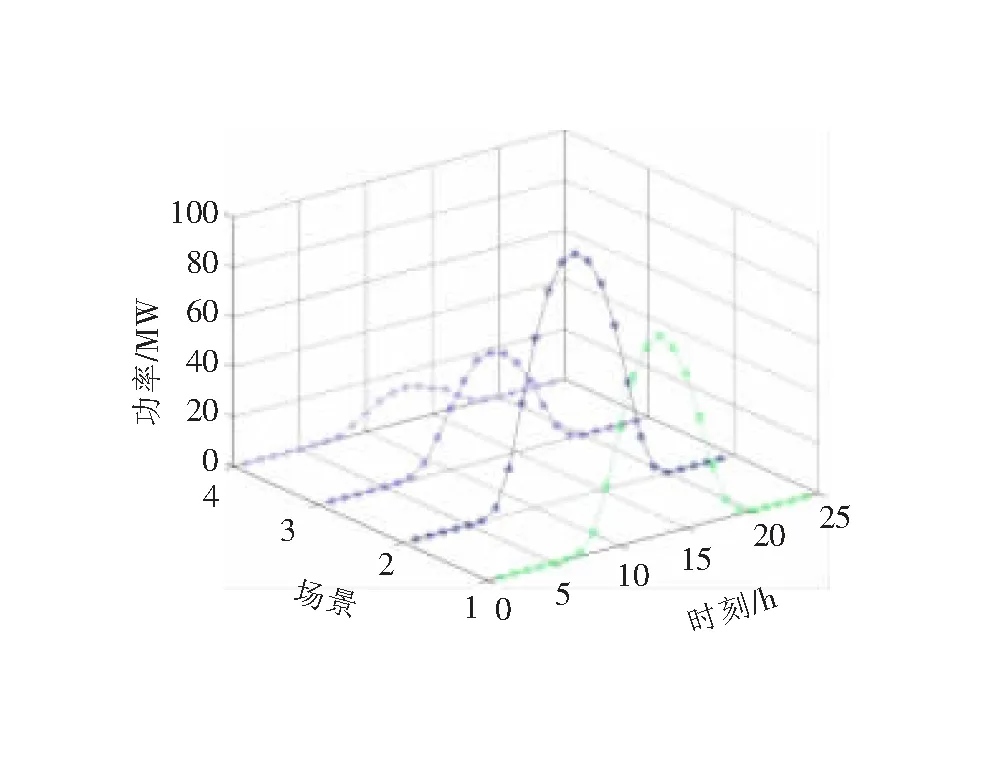
图5 分布式光伏典型场景出力图

设备参数如表1所示,单位容量光伏投资成本、单位容量储能投资成本以及其余参数如表2所示。

表1 设备参数

表2 系统规划的相关参数

4.2 算例结果

4.2.1 规划结果分析

基于文章提出的双层概率规划模型进行优化配置,所得日内运行结果如图6所示,优化配置结果如图7所示。

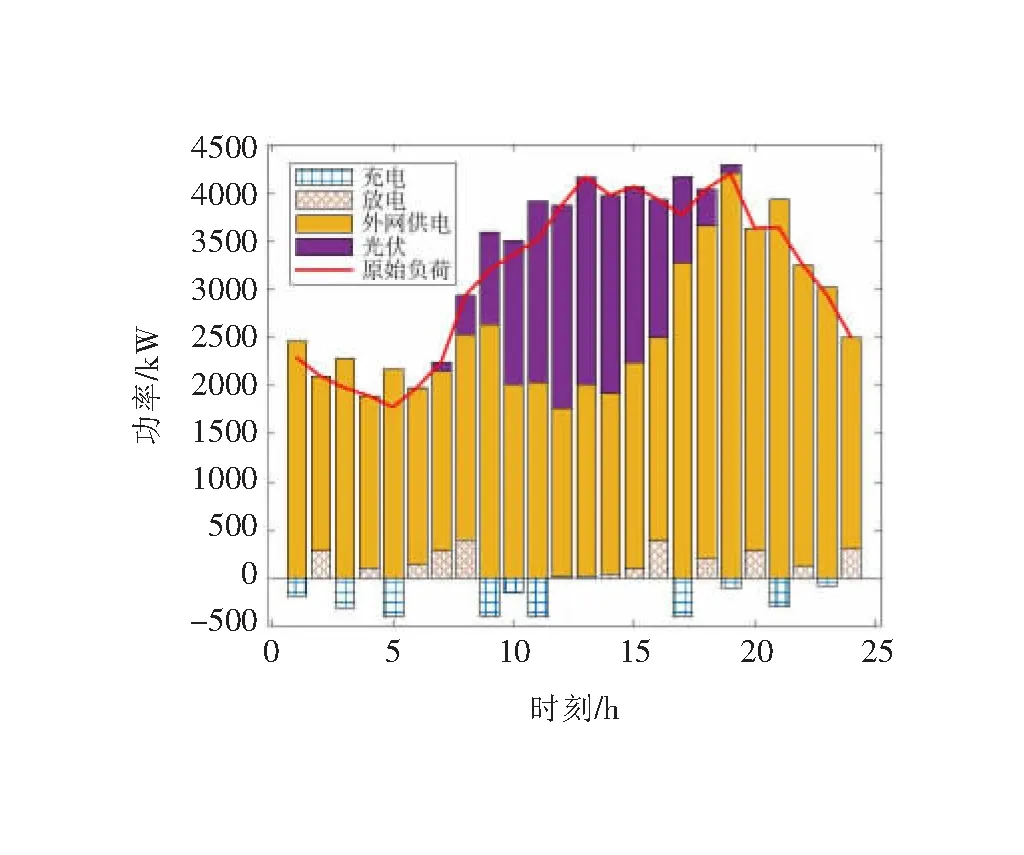
图6 优化后配电网日内功率图

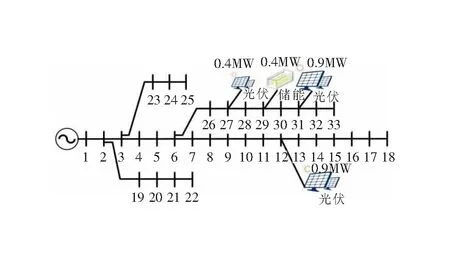
图7 优化配置结果

综合图6、图7得:考虑光伏不确定性时,分布式光伏主要安装于负荷较为集中的支路,符合分布式光伏的就近消纳原则,同时,12时前后的光伏出力高峰与负荷高峰叠加,减少了外部购电需求,有效提高了光伏利用效率;对于储能而言,考虑光伏不确定性后,储能设备将配置于分布式光伏较为集中的区域,并在9—11时、18—20时等时段通过充放电实现削峰填谷,从而有效平衡光伏出力波动,提高光伏消纳率,有利于提升配电网稳定性。

4.2.2 指标对比分析

为验证文章所提方法的有效性和优越性,设置了以下场景进行仿真对比:

1)场景1:不考虑光伏渗透率的配电网确定性规划;

2)场景2:考虑光伏渗透率的配电网确定性规划;

3)场景3(文章所提方法):考虑光伏渗透率的配电网概率规划。

仿真所得各场景分布式光伏配置容量对比结果如图8所示。

图8 分布式光伏配置容量对比结果

由图8得:场景3分布式光伏配置容量最高,相比场景1光伏配置容量增加700 kW,光伏渗透率提高47.50%;相比场景2光伏配置容量增加300 kW,光伏渗透率提高15.69%。表明通过考虑分布式光伏的不确定性进行分布式光伏优化配置有利于提高分布式光伏接入容量,挖掘分布式光伏并网潜力。

各场景优化配置指标对比结果如图9所示。

图9 优化配置指标对比结果

由图9得,相比场景1、场景2,场景3的购电成本分别降低107.64万元、75.78万元,网损成本分别降低4.30万元、3.63万元,电压偏差指数分别降低了16.67%和9.09%。这是因为传统方法基于确定性光伏出力进行规划,应对光伏出力波动的能力较弱,难以有效消纳剩余光伏出力,导致配电网在光伏发电低谷时段频繁向外部购电,传输损耗增大;而所提方法基于不确定性光伏出力进行光伏、储能规划,在提高光伏渗透率的同时,将分布式光伏配置在系统内负荷较为集中的支路,并对分布式光伏并网出力进行优化,提供电压与功率支撑,能够有效提升源荷匹配程度,降低外部购电量和网损,提高规划的经济性、可靠性。

4.2.3 网损对比分析

不同场景下的网损分布对比结果如图10所示。由图10得,相比场景1、场景2,场景3网损分别降低了8.47%、7.25%。这是因为传统方法根据确定性场景进行规划,获得的光伏、储能运行方案较为单一,难以适应多变的实际光伏运行情况。场景1缺乏对光伏渗透率的考虑,光伏接入量较小,令系统在重负荷时段难以形成有效的功率支撑,外部购电量较高,增加了传输损耗;场景2中难以良好消纳分布式光伏出力,引起系统内功率倒送,导致网损升高。由场景3结果可见,所提方法能够模拟光伏实际运行情况,在提升光伏接入量的同时优化光伏、储能运行方案,降低外部购电量并减少功率倒送现象,从而降低网损。

图10 网损对比结果

5 结束语

针对分布式光伏出力不确定性对配电网规划运行造成的经济性、稳定性挑战,文章提出了一种含高比例分布式光伏的配电网多目标概率规划方法,多场景算例对比表明,所提方法具有如下优势:

1)相较于传统规划方法,所提方法通过模拟光伏实际运行情况,有效挖掘分布式光伏并网潜力,提高光伏渗透率47.50%;

2)相较于传统规划方法,所提方法通过灵活优化光伏、储能运行方案,能够有效消纳光伏出力,在提升光伏接入量的同时减少了功率倒送现象,从而降低网损;

3)所提方法综合考虑光伏渗透率、经济性与稳定性目标,电压稳定性提高16.67%,综合成本降低37.65万元,兼顾了规划的经济性与稳定性。

在未来的研究中,将进一步研究不同种类分布式发电单元间的相关性对规划结果的影响,实现分布式能源和储能设备的相关性优化配置,以促进分布式能源消纳。