增量网络法矩阵形式的灵敏度分析方法研究

齐超,陈希有,杨旭强,杨春玲,于为雄

(1.哈尔滨工业大学,哈尔滨 150001; 2.大连理工大学,辽宁 大连 116024)

0 引 言

通常决策过程中所预测的自然状态概率及计算出的损益值,不一定十分精确,因此,往往需要对这些变动是否影响最优方案的选择进行深入研究,这就是灵敏度分析[1-4]。它是研究与分析一个系统(或模型)的状态或输出对系统参数(或周围条件)变化的敏感程度的方法,是电路容差分析、最坏情况分析和最优设计的重要基础,是电网络分析与综合的桥梁,在确定产品合格率、寿命及对工作环境的适应性方面起着关键的作用[5-9]。尤其在最优化方法中,经常利用灵敏度分析来研究原始数据不准确或发生变化时最优解的稳定性[10-11]。通过灵敏度分析可以确定哪些网络参数对系统(或模型)有较大的影响,这些参数的变化是否会导致网络函数或网络响应的变化,严重时影响网络正常工作[12-15]。对电测与仪表来说,灵敏度是衡量电气仪表输出对所测量参数变化敏感程度的一个重要标志,通过灵敏度的研究可加深对仪表的构造和原理的理解[16-18]。

传统增量网络法是指在原电路结构的基础上,添加额外的增量网络,在实际分析电路灵敏度的过程中需要先对原网络求解之后,才能分析出相应增量与各元件参数增量之间的关系,最终根据增量网络解得电路灵敏度,过程相对繁琐,且容易出错。与传统的增量网络法相比,矩阵形式的增量网络法仅需要确定原电路的各参数矩阵,直接求解电路灵敏度,无需额外增加网络即可求解[19]。可见增量网络法的矩阵形式具有分析简单、计算量小、可靠性高等优点。

1 绝对灵敏度

灵敏度一般包括绝对灵敏度、相对灵敏度和半相对灵敏度。网络函数H或网络响应R(统一可用T来表示) 对某元件相关参数p的变化率称为网络函数对该参数的绝对灵敏度,记作:

S=∂T/∂p

(1)

所以绝对灵敏度也称微分灵敏度。若将T表示为输出响应R(s)与不变输入激励E(s)的比值,有:

T(s)=R(s)/E(s)

(2)

代入式(1)整理得:

(3)

即:

(4)

所以网络输出响应R(s)对相关参数p的绝对灵敏度等于相应网络函数T对该参数的绝对灵敏度与输入激励乘积。

由上可见,只有简单电路才能求出网络函数或输出响应关于电路参数的显函数表达式,从而借助数学上求偏导数的方法得到绝对灵敏度。为了对较大规模电路网络进行灵敏度分析,并且便于编写灵敏度分析通用程序,须建立系统的灵敏度分析方法,如增量网络法、伴随网络法、符号网络法等。下面讨论增量网络法中,矩阵形式灵敏度分析含有受控源电路时,需要特别关注的一个问题。

2 问题提出与分析

增量网络法适用于当网络拓扑结构和激励固定不变,而元件参数发生微小变化时,网络响应对元件参数的绝对灵敏度分析。根据参考文献[20],节点电压方程矩阵形式为:

(5)

(6)

(7)

图1 电路网络1

依据图1得出网络线图如图2所示。

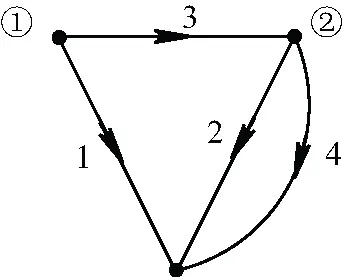
图2 网络线图

写出关联矩阵为:

支路导纳矩阵为:

(8)

支路独立源电压列矢量为:

支路独立源电流列矢量为:

进而得节点导纳矩阵为:

(9)

节点源电流列矢量为:

(10)

由式(9)、(10)得节点电方程为:

(11)

方程(11)的解为:

支路电压列矢量为:

进而得:

将上述结果代入增量网络法矩阵形式,分别得;

(12)

(13)

(14)

(15)

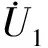
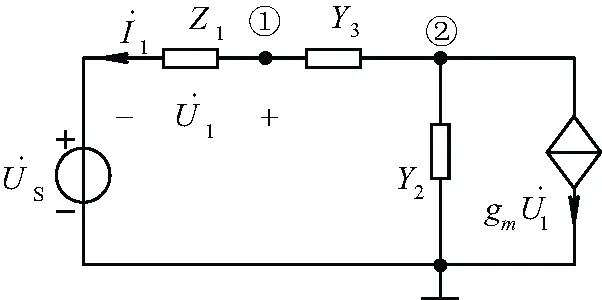
图3 电路网络2

通过广义支路学习可知,对于含有受控源的支路导纳矩阵Y的列写规则:当支路i是电压控制电流源(VCCS)时,它受支路j导纳上的电压控制,控制系数为gij,则支路导纳矩阵Y的i行j列元素将产生±gij的增量。当控制电压、被控电流分别与支路j和支路i方向一致时,gij前面取“+”号;否则,每改变一个方向,gij的前面变号一次。按照这一规则便可直接写出含有VCCS的支路导纳矩阵。如果暂且认为式(8)为图1的支路导纳矩阵,根据广义支路图4所示的支路方程矩阵形式要满足式(16)。

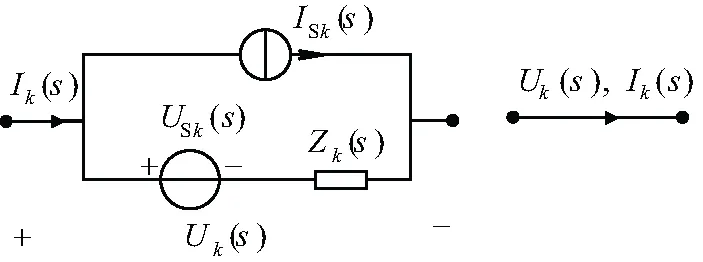
图4 广义支路及其线图

(16)

式中I为支路电流列矢量,U为支路电压列矢量。

那么由式(8)对图1电路就要满足如下的支路方程关系式:

(17)

(18)

对每一条支路列写电压电流关系有:

(19)

可见,基于广义支路约束,无法直接写出对应图的支路导纳矩阵。

3 问题讨论

那么对于受控源控制量包含独立电源参量的电路灵敏度分析问题,如何解决呢,笔者认为针对本例可以有以下三种方式。

1)解决方案一。

将图1中的支路1戴维南电路转化为诺顿电路,如图5所示。

图5 戴维南电路转化为诺顿电路

这样控制量就变成了阻抗元件上的电压,不再包含独立电压源参量。该等效电路支路方程的矩阵形式按照广义支路列写如下:

此时支路导纳矩阵即为式(8)。需要注意的是,这样等效变换后的图5中,独立电压源大小与阻抗参数Z1有关。

2)解决方案二。

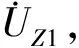
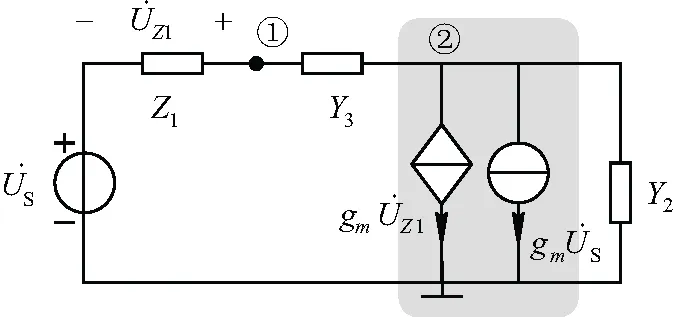
图6 VCCS等效变换电路

3)解决方案三。

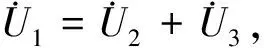
这样就解决了4支路方程列写问题,支路导纳矩阵满足了广义支路VCR方程式(16)。需要注意的是,如果其它支路还有纯电压源时就得另行考虑。

利用上述三种方法之一,等效后再列写支路VCR方程,就可得到标准的支路方程矩阵形式式(16),节点电压方程矩阵形式也和无受控源时候的式(5)一致。

4 灵敏度的求解

(20)

(21)

依据节点电压方程矩阵形式,代入具体数值求解节点电压如下:

解得:

(22)

进而得支路电压为:

(23)

整理得:

(24)

整理得:

(25)

整理得:

(26)

(27)

代入数值得:

可见此等式与式(24)相同。

代入数值得:

可见此式与式(25)相同。

代入数值得:

可见与式(26) 相同。

5 结束语

文章通过问题的提出与分析、问题讨论和解答过程可见,用增量网络法的矩阵形式分析电路绝对灵敏度时,需要掌握电路原理的本质、求解方法的适用范围和分析方法的多样性,具体总结如下:

2)控制量是否包括独立电压源虽然不影响节点导纳矩阵,但影响节点方程等式右侧的流入电流;

3)当控制量包含独立电压源时,不能套用标准的支路方程和节点电压方程的矩阵形式,因为这些形式都是基于阻抗或导纳上的电压为控制量而推导得出的;

4)可以通过等效变换的方法将受控源的控制量等效到阻抗或导纳元件上。

可见,只要透彻理解节点电压方程的实质是KCL方程,对电路参数求导不要有遗漏,就能找到问题所在。