交叉口大客车车辆换算系数研究
薄 雾,龚 栩,张 翔,梁舒同,雷艳红
(西藏大学工学院,西藏 拉萨 850000)
0 引言
车辆换算系数在研究道路通行能力、车头时距分布模型等方面具有重要的意义。该文立足于实际,为得出更加精准且适用于拉萨市交通状况的车辆换算系数,运用两种不同的算法并结合VISSIM 仿真,对拉萨市交叉口进行大客车车辆换算系数探究。车辆换算系数算法可分为以下几种,见图1。
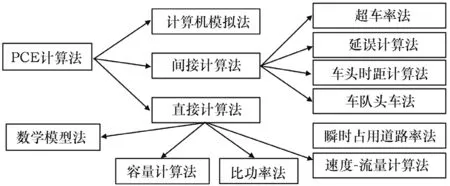
图1 车辆换算系数算法[1]
如图1 所示,车辆换算系数算法主要可分为三个大方向:直接计算法、间接计算法、计算机模拟法。该文采用将VISSIM 仿真结合车头时距法作为间接计算,将VISSIM 仿真与容量计算法结合作为直接计算,最终可得到适用于拉萨市的车辆换算系数值。
1 VISSIM 路网构建与数据设定
选取拉萨市江苏路与藏大西路交叉口作为仿真对象,利用VISSIM 仿真软件进行路网构建,静态车辆路径决策,数据输入(车流占比,路径决策期望,各方向流量,车流构成,期望速度分布,信号控制机),设置数据采集点。为消除行人对车辆造成的影响,不设置行人相关数据,减少误差。
为方便后文计算,在原实地调查的信号灯相位基础上,将该交叉口各进口道的直行和左转车道信号灯统一。统一后的直行车道和左转车道信号灯相位配时图见图2。
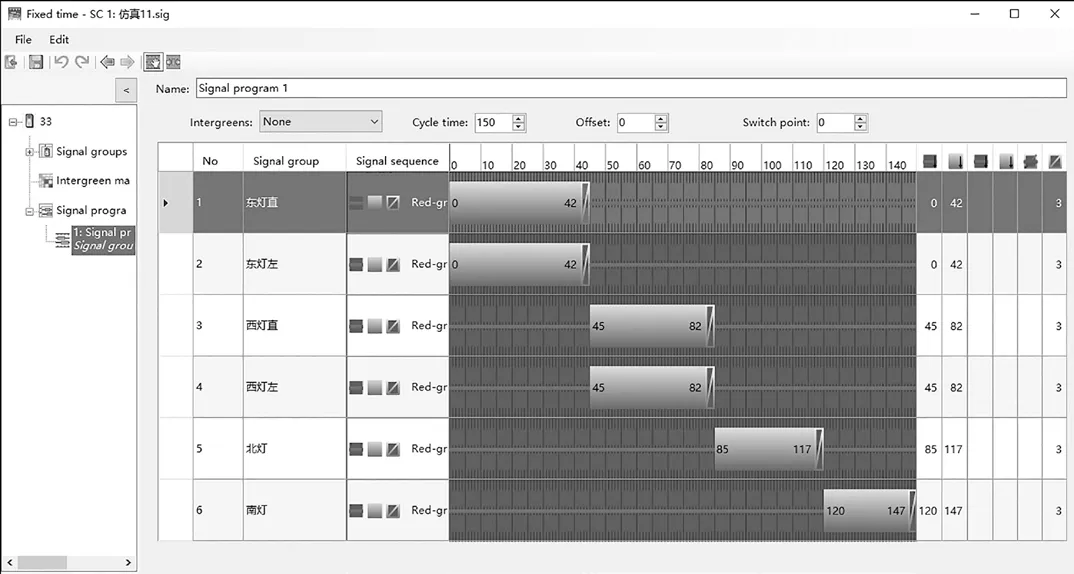
图2 统一后的各信号相位配时图
2 VISSIM 仿真结合车头时距法
2.1 VISSIM 仿真并计算大型客车饱和车头时距
设置车辆组成全是大型客车,大型客车期望速度分布为15 km/h,输入流量尽可能大,以达到仿真时该交叉口处于饱和状态的目的。仿真结果见图3。

图3 纯大客车流且期望速度分布为15 km/h 流量数据图
由图3 可得,仿真速度略低于设置的期望速度分布为15 km/h 的数值,说明在仿真时因为各种因素产生了一定的延误,使得车辆速度达不到设置的期望速度值,该情况符合实际。
为节约篇幅,纯大客车流在期望速度分布为不同值的流量数据图省略,具体流量数据结果见表1。
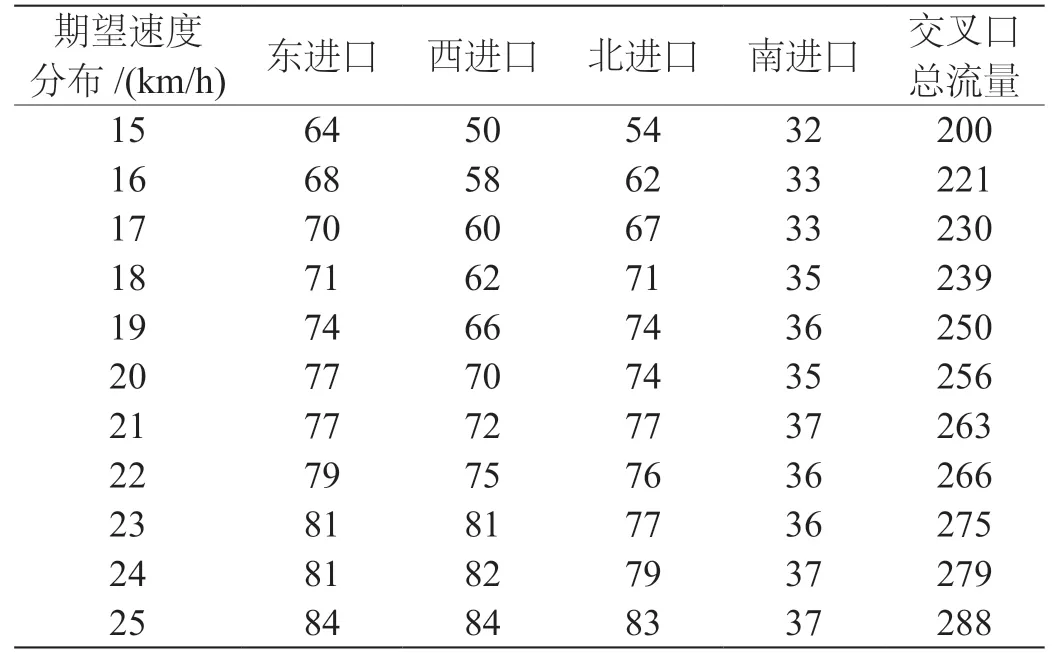
表1 不同期望速度分布下纯大客车流流量数据表
根据表1 的流量数据计算不同期望速度分布下的纯大客车流饱和车头时距,具体计算过程如下:
式中,C——通行能力(veh/h);h——饱和车头时距(s)。
由于在仿真模拟时,输入流量很大,该交叉口一直处于饱和状态,所以仿真流量q≈C。
流量q单位为每小时的车流量,且为连续车流,而仿真得出的表1 的数据qb是间断车流,且时间间隔为450 s,为了让单位统一并得到连续车流数据,需要将图表中的数据qb进行转化。
式中,q——VISSIM 仿真统一单位和车流情况后的进口道流量(veh/h);qb——仿真得出的表1 的进口道流量数据;N——某进口道车道数;t——仿真时间间隔(为450 s);T——信号周期(为150 s);Ge——绿灯时长(s);——该交叉口平均饱和车头时距(s)。
经过式(1)至式(5)的计算,纯大客车流饱和车头时距见表2。
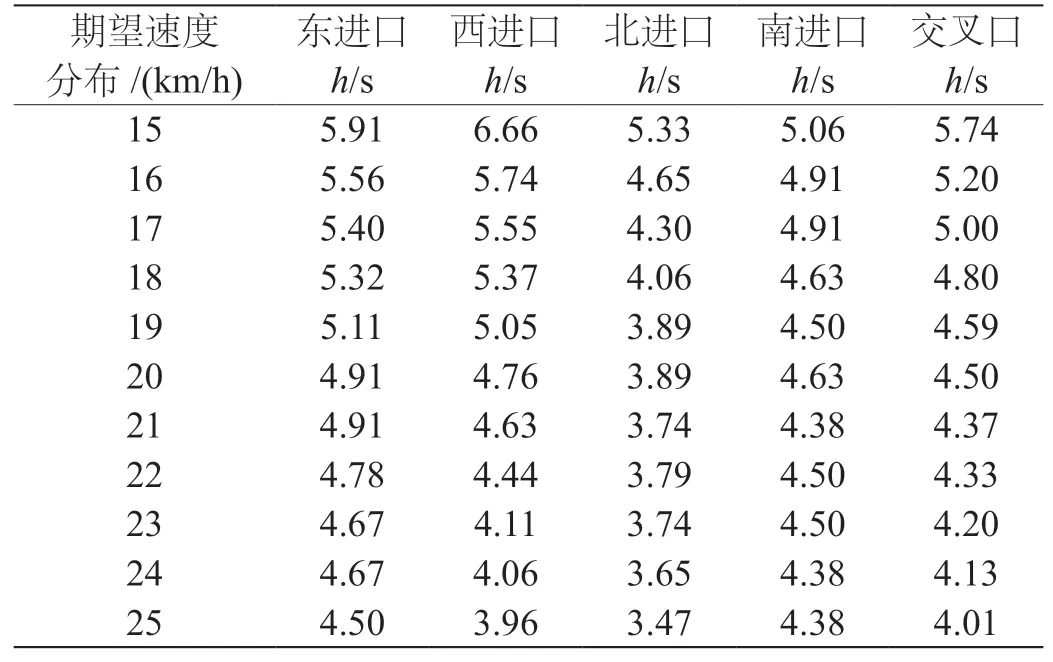
表2 不同期望速度分布下纯大客车流饱和车头时距
2.2 车头时距法计算大客车车辆换算系数
车头时距作为评估行车安全的重要指标,其与交通组成以及驾驶员的驾驶行为有着紧密的相关性。不仅如此,车头时距作为一项重要依据还可以直观反映道路通行能力和服务水平,同时在改进道路设计、改善服务水平以及优化交通管理等方面占据重要地位。利用车头时距计算车辆换算系数的算法如下:
式中,PCEi——i种类型车辆的车辆换算系数;hi——i种类型车辆的车头时距(s);hc——标准车的车头时距(s)。
标准车的车头时距在拉萨市江苏路与藏大西路交叉口实地观测得出,观测时需要注意以下事项:①观测车头时距应该观测整个车队的平均车头时距,而不是单独车辆的车头时距;②观测的起始车辆一定要从车队的第3至第5 辆车开始计时,这样做的作用是为了消除由于启动延误带来的时间和统计车辆数的误差;③当观测的车队混有其他非标准车时,应该放弃观测,因为非标准车会对跟驶车辆造成一定的影响。
根据实地观测数据,得出拉萨市江苏路与藏大西路交叉口的标准车车头时距,见表3。

表3 实地观测标准车车头时距
利用式(6),可得出不同期望速度分布下的大客车车辆换算系数,计算结果见表4。令期望速度分布为20 km/h 的大客车车辆换算系数为拉萨市交叉口大客车车辆换算系数推荐值,见表5。
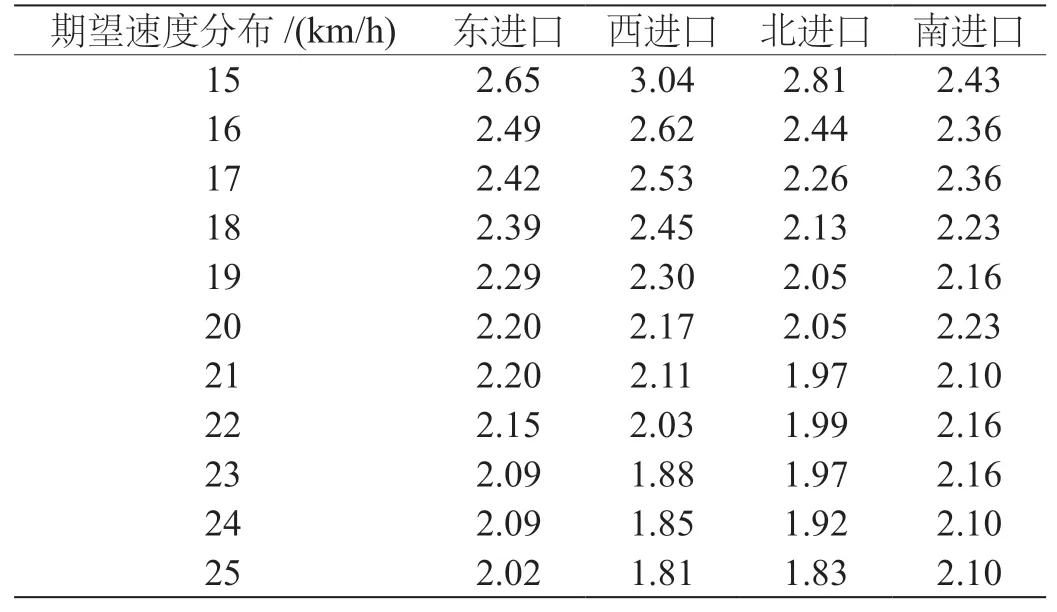
表4 不同期望速度分布下的大客车车辆换算系数

表5 拉萨市交叉口大客车车辆换算系数推荐值
3 VISSIM 仿真结合容量计算法
3.1 VISSIM 仿真纯标准车流的流量数据
由于我国十字交叉口限速为30 km/h,设置车辆组成全为小汽车,期望速度分布为30 km/h,仿真结果见图4。
其他数据不变,在车流中添加大客车,设置占比为10%,大客车期望速度分布取20 km/h,仿真结果见图5。

图5 车流大客车占比10%,大客车期望速度分布为20 km/h 的流量数据图
3.2 容量计算法计算大客车车辆换算系数
容量计算法模型是认为在同一服务水平下,混合车流的车流量应该与纯小汽车车流量具有等价性,基于该理论,得出容量计算法模型,即:
式中,qb——某服务水平下对应的纯小汽车流量(veh/h);qm——某服务水平下对应的混合车流量(veh/h);p——混合车流中的大客车比例。
根据式(7),图4 的流量数据为qb,图5 的流量数据为qm,大客车比例p为10%,将数据代入,可得到各进口道的大客车车辆换算系数,结果见表6。

表6 基于容量计算法模型得出的大客车车辆换算系数表
4 结语
该文利用VISSIM 仿真分别结合车头时距法和容量计算法探究交叉口大客车车辆换算系数,在大客车期望速度分布为20 km/h 时,得到的结果见表5、表6,即利用VISSIM 结合车头时距法得到的东、西、北、南进口车辆换算系数分别为2.2、2.17、2.05、2.23;利用VISSIM结合容量计算法得到的东、西、北、南进口车辆换算系数分别为1.94、1.9、2.4、1.69。
两种方法得到的结果具有一定的差异性,究其原因,是因为两种算法的出发点不同。车头时距法属于间接计算,从车头时距的角度出发考虑车辆换算系数;而容量计算法属于直接计算,从交通流量的角度出发考虑车辆换算系数。所以研究车头时距和其分布模型时,车辆换算系数应该用VISSIM 结合车头时距法得出的结果;研究交通流量时,车辆换算系数应该用VISSIM 结合容量计算法得出的结果。

