小学数学教学中渗透数学思想方法的策略
文/欧阳燕平
数学思想方法是数学思想和数学方法在数学学科的有机整合,如分类思想方法、数形结合思想方法、符号化思想方法等[1]。数学思想方法蕴含在数学知识中,是对数学知识的理性认知,具有概括性、内隐性、实用性、层次性等特点,有极强的教育价值。
在数学教学中渗透数学思想方法,可以使学生知道“从什么角度出发思考问题”和“用什么样的数学方法解决问题”,由此掌握数学知识,同时获取相应的思想方法,增强数学学习效果。鉴于此,教师要把握时机,在小学数学教学过程中积极地渗透数学思想方法。
一、在分析知识的过程中挖掘数学思想方法
挖掘数学思想方法是渗透数学思想方法的基础。数学思想方法隐藏在数学知识背后。要想有效渗透数学思想方法,教师要分析数学知识,透过数学知识,挖掘其中的数学思想方法。
以“数一数”为例,教材在准备课的开篇呈现了以下情境图(如图1)。

图1 教材插图
该情境图中蕴含着数学知识——数数。在数数的过程中,学生要做到不遗漏、不重复,这体现了数学思想方法中的对应思想。数数的过程正是学生进行统计的过程,其中蕴含了统计思想。此外,在数数的过程中,学生要将同一种事物看作整体,这就蕴含着集合思想。由此可见,“数数”这一知识点蕴含着对应思想、统计思想和集合思想。在课堂教学中,教师可以情境图为立足点,引导学生利用不同的方式数数,以学生数数的过程为入手点,渗透不同的数学思想方法,促使学生建构相关认知。
二、在知识的发生过程中体悟数学思想方法
知识的发生过程正是数学思想方法的发生过程。数学知识的发生过程,包括数学概念的形成过程、数学规律的揭示过程等,极具层次性,蕴含着数学思想方法[2]。在此过程中渗透数学思想方法,可以使学生经历从个别到一般、从具体到抽象、从感性到理性的认知过程,由此扎实掌握数学知识,同时获取数学思想方法,增强数学学习效果。所以,在数学教学中,教师应把握时机渗透数学思想,引导学生体悟数学方法。
以“乘法的初步认识”为例,“几个几”是本节课的重点内容,也是学生理解乘法的关键。同时,此内容中蕴含着转化思想和乘法意识。
基于此,在课堂上,教师先利用交互式电子白板呈现小动物活动图片,向学生提出问题:“数一数图片上的小动物,兔子有多少只?鸡有多少只?”在此问题的驱动下,学生用不同的方法数数,最终正确数出了兔子和鸡的个数。同时,学生体验了统计思想、集合思想。然后,教师鼓励学生畅所欲言,介绍自己数数的方法。有的学生说道:“我两个两个地数,数出三次,数出6 只兔子;三个三个地数,数了四次,数出12 只鸡。”按照学生的说法,教师在黑板上写出算式“2+2+2=6”和“3+3+3+3=12”,让学生感受转化思想。立足算式内容,教师发问:“这两个算式有什么共同特点?”学生细心对比,发现算式中都是2 的相加,3的相加。教师对此进行赞赏,并提出任务:“请大家拿出材料包中的圆片,将每2 个摆成一堆,摆出4 堆。请用加法算式进行表示,试着写出结果。”
受到此任务的驱动,学生边摆放边观察边思考,列出算式“2+2+2+2=8”。之后,教师提出其他任务:“8个圆片,每堆摆4 个,能摆几堆?”学生们继续操作,列出算式“4+4=8”。于是,教师在黑板上写下两个算式,引导学生对比。在对比的过程中,学生认真思考,发现“2+2+2+2=4+4”。教师鼓励学生用自己的语言进行描述。有学生描述道:“4 个2 相加的结果,和2 个4 相加的结果相同。”教师趁机引出乘法内容:“我们还可以用乘法计算4 个2 和2 个4 相加的结果。”与此同时,教师板书:2×4=8,4×2=8。基于此,教师鼓励学生进行描述。在课堂已有认知的支撑下,学生纷纷进行描述:“2×4 表示4 个2 相加。4×2 表示2 个4相加。”“2×4 表示2 个4 相加。4×2 表示4 个2 相加。”通过这样转化数学文字语言和数学符号,学生知道了乘法的含义,加深了对所学的理解。
由此可见,引导学生经历知识的发生过程,可以使学生一步步地掌握数学知识,同时顺其自然地体悟集合思想、统计思想、转化思想等。
三、在问题的解决过程中凸显数学思想方法
问题解决过程是学生探究数学知识,获取数学思想方法的过程[3]。在解决问题的过程中,学生会自觉应用数学思想方法,由此增强认知,强化问题解决能力。所以,问题解决的过程正是渗透数学思想方法的良好时机。在数学教学中,教师要依据教学内容,呈现相关问题,尤其要以问题的解决过程为时机,渗透数学思想方法。
以“鸡兔同笼”为例,在课堂上,教师在交互式电子白板上出示《孙子算经》中的“雉兔同笼”问题,引导学生阅读、思考,将其翻译为白话文。之后,有学生复述:“笼子里有鸡和兔子。从上数,鸡和兔子一共有35 个头;从下数,鸡和兔子一共有94 只脚。鸡和兔子各有多少只?”教师对此进行赞赏,并鼓励学生进行解答。但此时,部分学生脸上露出疑惑的神色。教师把握时机,引出“化繁为简”这一审题策略,同时呈现简化后的问题:“笼子里有鸡和兔子。鸡和兔子一共有8 个头、26 只脚。鸡和兔子各有多少只?”在提出问题后,教师给予学生充足的时间,让学生选用不同的方式解决问题。
在规定的时间结束后,教师组织展示活动。在活动中,有学生提到列表法:“假设有1 只鸡、7 只兔子,此时会有30 只脚,不符合题意,继续列表,直到有3 只鸡、5 只兔子脚数符合题意。”教师在赞赏的同时,提出问题:“如果数字变大,我们是否还能用这种方法?”大部分学生表示否定。于是,教师鼓励其他人介绍其他方法。此时,有学生提到画图法:“先画出8 个头,在每个头下画出2 只脚,全部表示鸡。此时,一共有16只脚。与原题相比,少了10 只脚,需要添加10 只脚。”在该学生介绍到此时,教师鼓励该学生上台画图。其他学生认真观看,提出问题:“为什么不是一只一只地添加脚,而是两只两只地添加脚?”台上的学生作答:“因为一只兔子比一只鸡多两只脚,所以两只两只地添加。添加五次脚数就足够了,这五次就是将5 只鸡换成5 只兔子,也就是说有3 只鸡,5 只兔子。”其他学生表示理解。于是,教师趁机总结解题方法,并揭露其中蕴含的数学思想方法——数形结合法。之后,教师按照此方式,引导其他学生继续展现其他解题方法。
实践证明,学生通过体验问题解决活动,积极思维,解决了问题,建构了数学认知,尤其掌握了不同的解题方法。同时,学生也感受到了不同方法中蕴含的数学思想和方法,有利于提高问题解决水平。
四、在知识的总结过程中归纳数学思想方法
知识总结过程既是学生总结数学知识点的过程,又是学生归纳数学思想方法的过程[4]。在数学课堂上,学生通过体验多样活动,不但掌握了数学知识点,还习得了数学思想方法。在课堂总结环节,教师要立足学生的学习情况,提出总结任务,促使学生回顾课堂学习过程、归纳知识点和数学思想方法,达到查缺补漏、建构完善认知、增强课堂学习效果的目的。
以“三角形的分类”为例,本课涉及分类思想。立足于此,在课堂上,教师组织分类活动,引导学生与小组成员合作,从不同的角度对三角形进行分类。在此过程中,大部分小组从边和角入手,对三角形进行分类,了解了直角三角形、等腰三角形和等边三角形,同时获取了分类思想。于是,在课堂总结环节,教师提出如下任务:“请大家回顾课堂学习内容,利用韦恩图,对三角形进行分类,展现三角形的分类结果。”在此任务的驱动下,学生积极进行头脑风暴,在脑海中呈现出三角形分类的全过程,由此了解不同的三角形及关系。之后,学生发散思维,依照边和角对三角形进行分类,呈现出不同的图像。实际上,学生绘图的过程,正是学生转化分类思想的过程。在此过程中,学生会增强对分类思想的认知。
在学生做出图像后,教师随机选择一幅作品(如图2),并鼓励学生代表依据图像内容,介绍三角形的分类依据和结果。
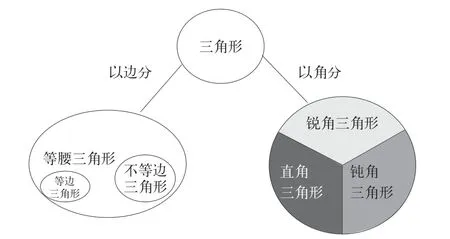
图2 学生作品
学生代表介绍之后,其他学生提出问题,如“等腰三角形和不等边三角形之间是否存在关系?存在怎样的关系?”“等边三角形是特殊的等腰三角形吗?”等。学生代表面对一个个问题认真作答,同时借此完善自己的图像内容,以增强认知能力。
如此做法,不但使学生应用了数学思想方法,梳理了数学知识点,加深了对数学知识的理解,还使学生顺其自然地归纳了数学思想方法,增强了对数学思想方法的认知。
五、在知识的运用过程中使用数学思想方法
学生运用数学思想方法是渗透数学思想的重要目的,知识的应用过程是学生使用数学思想方法的过程[5],而课堂练习、课后作业是学生应用数学知识的主阵地。在数学教学中,教师应以知识的应用为抓手,联系学生的学习所得设计相关习题,由此组织课堂练习活动和课后作业活动,促使学生迁移已有认知,用数学思想方法解答习题。
以“集合”为例,学生在课堂上体验情境活动,感知了集合圈的形成过程,感受了集合思想。但是,学生受到学习差异影响,学习水平不尽相同。于是,教师立足教学内容和学生学习差异,分层设计习题,使每个学生都有运用数学思想方法的机会。教师具体设计了如下习题:

图3
学生依据自身学情,自选相应难度的题目。在解决习题时,学生迁移集合思想方法,解决相关问题,由此强化集合思想,锻炼问题解决能力。
六、结束语
综上所述,有效渗透数学思想方法于数学教学,可以使学生掌握数学知识,获取数学思想方法,提高数学学习水平。所以,教师在小学数学教学中可以依据数学教学内容,把握教学时机,运用多样策略,渗透数学思想方法,引导学生经历数学原理推导过程、数学问题解决过程、数学知识总结过程和数学知识应用过程,进而扎实掌握数学知识,获取数学思想方法,提升数学学习质量。

