2024铝合金切削过程微观力学强化机理研究

宋 徽 张国智

（1.建筑学院，新乡职业技术学院，新乡 453000；2.机电工程学院，新乡学院，新乡 453000）

1 引言

切削过程是机械制造中最为常见的过程，长期以来人们试图在实际加工之前对这一过程进行计算机模拟和理论模型的建立[1]，以及相关刀具性能模拟[2]，提出了很多理论模型，最早提出了剪切角的理论切削模型，此外，国内外学者还提出了很多的切削过程的模拟模型，但还没有一个准确的模拟模型。但切削过程中切削力的计算已较为成熟，提出了很多切削力的理论和经验的计算模型[3，4]，并且与实际实验结果吻合较好。但切削过程是较为复杂的过程，也是一个高度非线性热结构场耦合分析[5]，因而，要想准确地对这一过程进行计算机模拟，需要在机理上研究材料在切削加工过程的力学性能的变化。在模拟切削过程中，最难解决的是两个问题：一是切屑形成与断裂准则；二是加工完成后工件表层力学性能的变化。但这对于预测工件加工变形及残余应力至关重要。此外，对于机械表面失效分析也很关键[6]。2024铝合金广泛应用于航空航天、建筑装潢中，目前，关于此材料切削强化的机理性研究还不是很深入系统。本文以有限元数值计算为仿真手段，在对切削过程进行模拟的基础上，从微观塑性力学的角度揭示切削过程中表层材料力学性能的变化机理。

2 基于仿真技术的切削过程机理分析方案

基于有限元仿真手段，首先建立切削过程的耦合场分析的有限元模型，在对切削过程的应力场及温度场分析结果的基础上，对局部切削点的组织结构在切削过程中的变化进行分析，然后，在有限元仿真分析的基础上，基于微观塑性力学理论，对材料在切削过程中的力学性能变化进行机理上的分析与研究。具体的分析流程如图1所示。

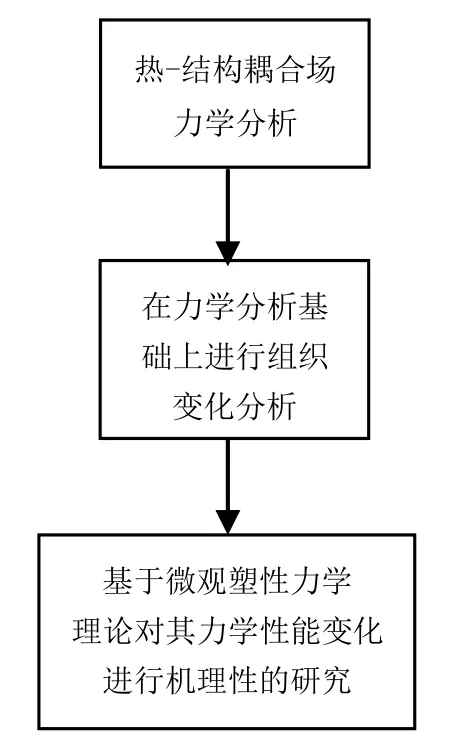
图1 切削过程力学机理仿真分析流程

3 切削过程的有限元分析

3.1 应力及温度分析

建立了切削过程的热结构场耦合分析的有限元模型，有限元模型图如图2所示，材料选用的是2024铝合金，初始加工温度为20℃，选用的刀具为TNMA332，刀具参数示意图如图3所示，各参数分别为：IC=9.53，T=4.76mm，R=0.8mm，B=13.494mm，H=3.81mm。切削时，切削参数为：切削速度为250mm/s，进给速度为0.35mm/r，切削深度为 0.3mm。热传导系数为45N·s-1·mm-1·℃-1，切削长度为3.5mm，剪切摩擦系数取为0.5，计算的迭代步数为10000，在计算的过程中，使用网格重划分技术。

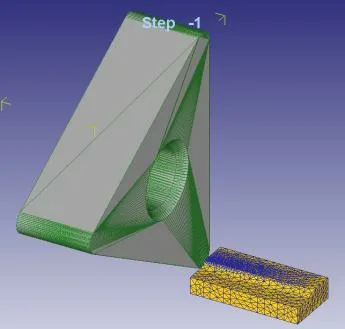
图2 切削过程的有限元模型图

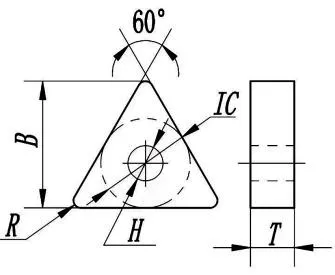
图3 刀具参数示意简图

切削过程完成时的结构场的有限元分析结果如图4所示，从图4a 中可见，在局部切削处的等效应力很大，应力分布极不均匀，从图4b 中可见，切削区域处的某点在切削过程中随着切削的进行应力逐渐增大。

切削过程完成时的温度场的有限元分析结果如图5所示，从图5a 中可见，在局部切削处的温度有很大的升高，在局部最高温度为327℃，温度场分布极不均匀，图4b 中的节点在切削过程中的温度变化如图5b所示，从图5b 中可见，该点在切削过程中随着切削的进行温度逐渐升高，主要是由摩擦热及塑性功转化成热能造成的。

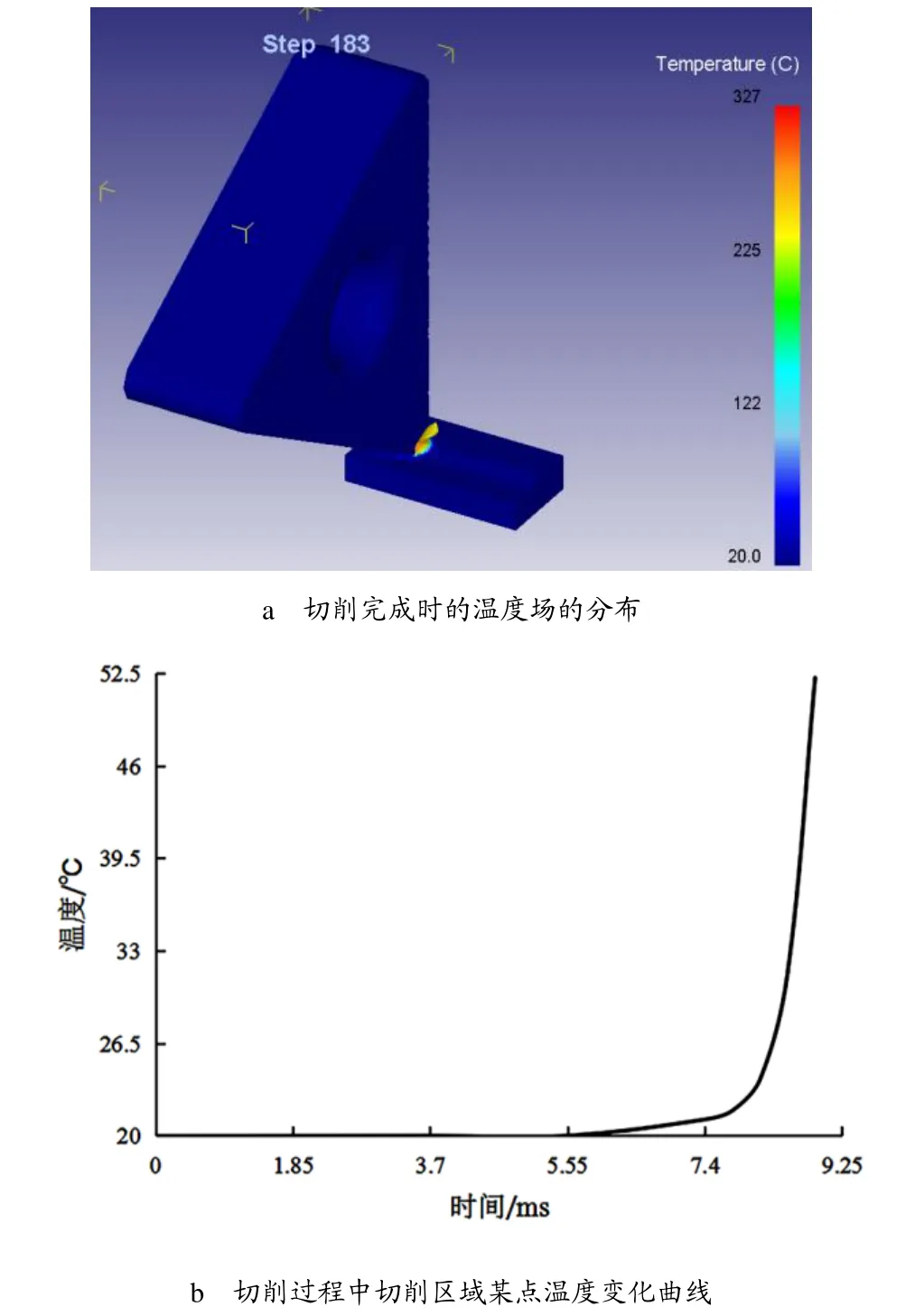
图5 切削过程的温度场的有限元分析结果

3.2 组织变化分析

在切削过程的热结构耦合场分析结果的基础上，对切削过程中组织结构的微观变化进行了进一步计算，得出切削过程中切削区域中局部塑性变形后，在组织结构上的具体变化，如晶粒尺寸、晶界、位错密度等。在计算过程中，选取了切削完成时刻的切削根部点作为微组织结构计算区域，并对远离切削区域的点进行计算。如图6所示，在计算过程中，选取的计算区域为3mm×5mm，放大因子为2。对比图6a 和图6b 可知，在切削过程中，切削区域组织结构发生了较大变化，晶粒尺寸和位错密度显著增加，所以，在切削区域发生了加工硬化现象，而远离区域变化较小。

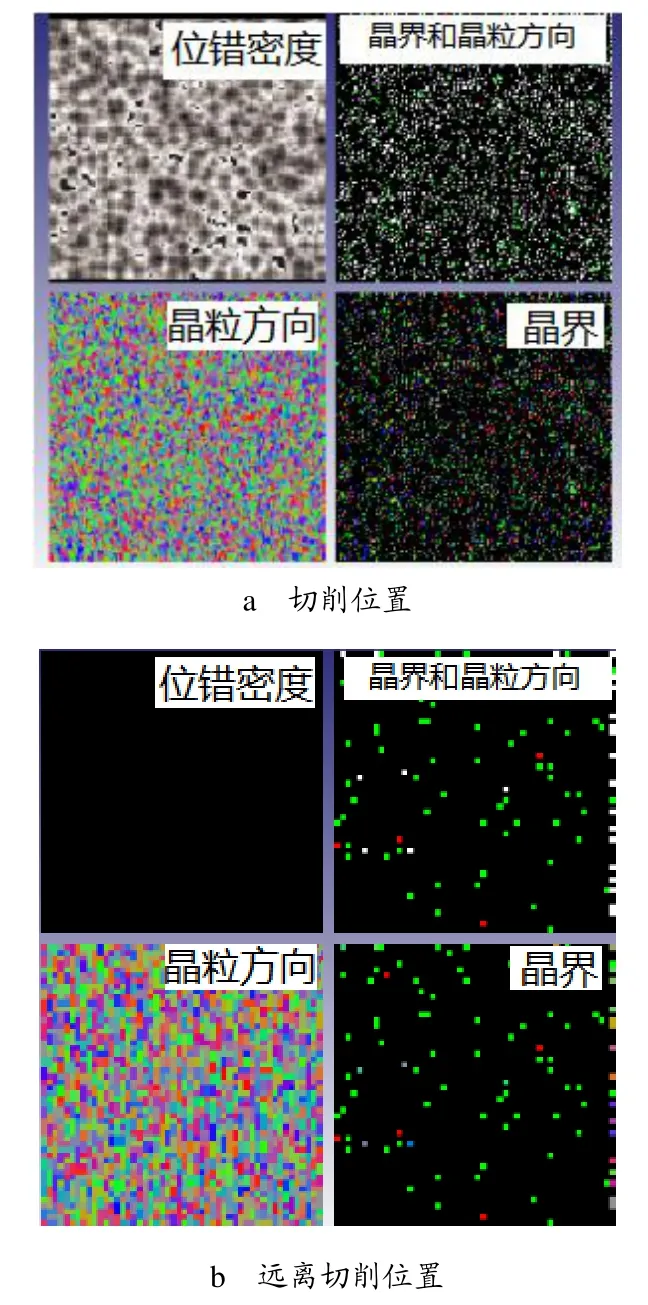
图6 组织变化计算结果

3.3 力学机理分析

切削过程中组织结构的变化造成了对其切削表层材料力学性能主要参数的影响，如弹性模量、泊松比、屈服应力、刚性模量等。切削表层材料的力学性能变化不仅对表面的各种力学性能产生了较大影响，而且对于其工件表面的加工变形及其中的残余应力产生了较大影响。对其工件的表面变形及其内部残余应力的计算准确，需分析其在切削过程中表层材料力学性能的变化。

基于微观塑性力学理论可知，弹性模量、泊松比在切削过程中受晶粒结构的变化影响较小，可近似认为不发生变化，而材料的塑性指标如屈服应力发生了较大的变化，但刚性模量，即双线性硬化材料模型的第二条曲线的斜率几乎不发生变化。

根据微观塑性力学中的MSG（mechanism-based strain gradient）理论和Hall-prtch 准则，切削加工后表层材料的屈服应力可由式（1）计算：

其中，σs为材料的初始屈服应力（表层材料切削完成后的屈服应力）；G为剪切模量；b为Burgers矢量；α0为Taylor系数，其值约为0.3；ρ为位错密度，产生于材料中的非均匀塑性变形；M为Taylor因子，对面心立方多晶体（fcc）金属材料，M=3.06；k为Hall-prtch参数；d为平均晶粒尺寸[7]。

根据文中组织分析的有限元计算结果、相关实验、文献，σs=250MPa，G=27GPa，b=0.281nm，α0=0.3，M=3.06，ρ=1.4×1013m-2，k=4.8MPa/μm0.5，d=18μm，根据式（1），计算得出2024铝合金表层材料在切削完成时的屈服应力增加了46.42MPa。拉伸实验图如图7所示，图7b为工程应变与工程应力的拉伸曲线，由图7b可见，切削后的试件未做去除应力处理与去除应力处理后相比，强度略有提升，屈服应力处的增加值与文中计算的增加值的误差仅为6.75%，与文中分析结果相符。当然，表层材料在切削完成时的屈服应力增加值与各种加工参数相关，如切削速度、进给量、切削深度等。由此可知，材料经过切削加工后表层材料的塑性力学性能参数发生了较为明显的变化。

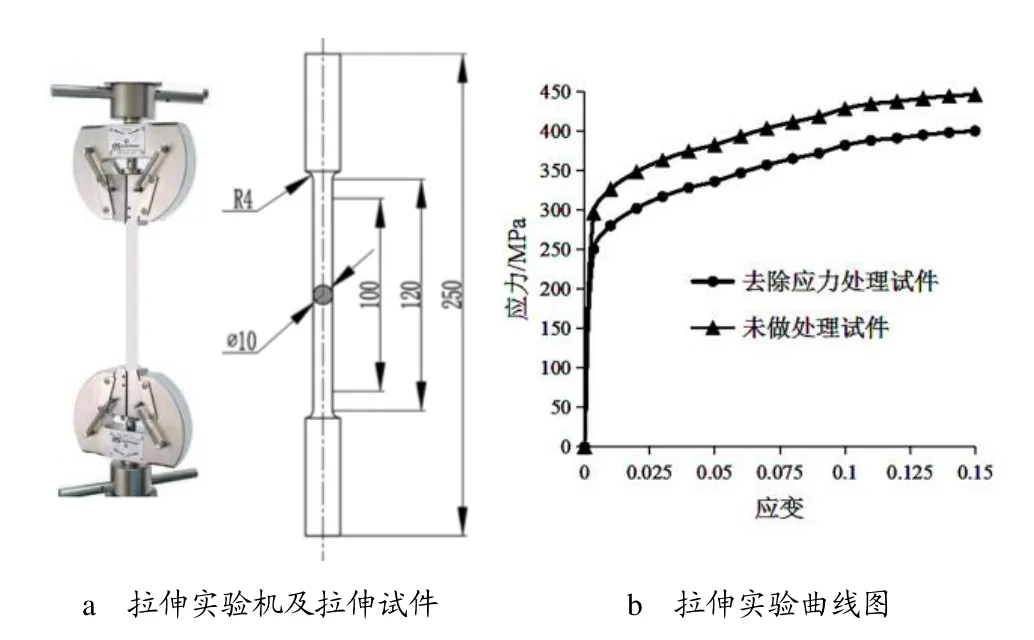
图7 拉伸实验图

铝合金布氏硬度和抗拉强度转换关系如下：

2024铝合金未切削试件的表面硬度实验检测其硬度值的布氏硬度为117，代入式（2）中得其抗拉强度为403.65MPa，切削试件的表面硬度实验检测其硬度值的布氏硬度为131，代入式（2）中得其抗拉强度为451.95MPa，增加了48.3MPa，与根据式（1）计算的抗拉强度增加值的理论计算值的误差为3.89%，这个误差比拉伸实验的误差小，表明表面硬度实验更能直接反映切削后2024铝合金的表层抗拉强度略有增加，进一步验证了本文的仿真和理论分析的准确性。

综上所述，经过切削加工后，实际加工表面的材料力学性能由于组织结构的变化而发生了很大变化，尤其其塑性性能指标，如屈服应力，主要是晶粒尺寸与位错密度造成的，因而，对加工后的零件进行精确分析计算及对表面加工变形或残余应力计算时，必须考虑晶粒尺寸与位错密度等组织结构的变化造成的表层材料塑性性能变化，并在此基础上建立动态的本构模型，从而对零件的工作性能及表面的摩擦磨损性能进行更精确地分析计算。

4 结束语

本文针对切削过程中表层材料力学性能的变化进行研究，首先，结合微观塑性理论，提出了基于有限元仿真的分析方案，建立了切削过程的热结构场耦合分析的有限元模型，并对典型参数的切削过程进行了有限元模拟，在切削局部最高温度为327℃；其次，在此基础上进行了切削过程中微观组织的计算，得到了切削区域及远离切削区域处的晶粒方向、位错密度、晶界分布，可知，切削区域组织结构发生了较大变化，晶粒位错密度显著增加，其数值为1.4×1013m-2；最后，基于MSG 理论和Hall-prtch 准则，通过计算，2024铝合金表层材料在切削完成时的屈服应力增加了46.42MPa，这与实际测试结果相符，误差仅为6.75%，抗拉强度增加值与表面硬度实验的检测值误差为3.89%。本文的研究对切削过程的精确模拟、表面加工变形的精确计算、表面摩擦磨损性能的精确分析具有工程应用和理论研究价值。