依托主题大概念 建构单元大整体

王平　任建波

［摘 要］“数与运算”主题教学的重点包括让学生感悟数的认识与数的运算之间的密切联系，理解四则运算之间的关系，感悟运算的一致性等。“分数与整数相乘”是这一主题的重要内容，包含乘法的意义、算理一致性和分数特殊性三个方面的大概念。文章根据上述分析的主题大概念对“分数与整数相乘”的教学进行了流程探究，旨在为广大教师提供教学借鉴。

［关键词］主题大概念；计算教学；分数与整数相乘 ；单元链

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2023）23-0006-04

“分数与整数相乘”是苏教版教材六年级上册“分数乘法”单元的起始内容，是“数与运算”主题的重要内容。《义务教育数学课程标准（2022年版）》指出，这一主题教学的重点包括感悟数的认识与数的运算之间的密切联系，理解四则运算之间的关系，感悟运算的一致性等。即数的认识是运算的基础，通过数的运算有助于学生更好地认识数；四则运算本质上是计数单位多少的表达，加法和乘法是计数单位个数的累加，减法和除法是计数单位个数的细分。在内容分布上，“乘法运算”在小学三个学段中都有相应的安排，呈现螺旋上升、不断丰富和深化的特点（见表1）：第一学段了解意义、感悟关系、探索算理和算法；第二学段探索并掌握多位数的乘法，进行混合运算和理解运算律；第三学段进行小数、分数的运算，感悟运算的一致性，包含乘法的意义、算理一致性和分数特殊性三个方面的大概念。

基于以上认识，笔者依据主题大概念对“分数与整数相乘”进行了整体性设计，横向关联，揭示乘法意义的一致性，即表示几个相同整数、小数、分数相加的运算；纵向贯通，体现整数、小数和分数乘法算理本质的一致性，即均是求计数单位的个数。

【教学片段一】创设情境，整体进入

师：还记得我们是怎样庆祝国庆节的吗？我们通过当时的照片回忆一下。

出示图文信息（图略）：（1）一年级举行了庄重的入队仪式，邀请部分优秀少先队员代表参加，他们的座位为低、中、高三个方阵，每个方阵20个座位；（2）校园展出优秀书法、绘画和手工作品，每种作品有30件；（3）游园活动大约20项，参与一个项目平均需要0.09小时；（4）游艺活动的奖品特别丰厚，每个年级的经费为0.2万元。

师：你能从以上信息中获得哪些数学信息？会列算式表达吗？列算式后选择其中一道算式，说一说它表示的意思。

生1：优秀少先队员代表的人数为20×3，表示3个20相加。

生2：参加全部游园活动大约需要0.09×20小时，表示20个0.09相加的和。

师：怎样计算？说说你计算的道理。

生3：20×3就是2个十乘3得6个十，6写在十位上，就是60。

生4：0.09×20也是这样，先算出有180个0.01，就是1.8。

师：这些是大家已经学过的整数和小数乘法，分数乘法的意义会不会有变化？计算方法有没有独特之处？今天我们就来研究一下。

【思考】课始选取学生有亲身体验的国庆节庆祝活动作为导入情境，呈现活动中的场景和信息，引导学生进行数学化的表达和说理，可激活学生关于整数、小数乘法意义以及算法、算理的经验。一方面将分数乘整数的学习融入乘法学习的整体中，另一方面给予学生回顾、沟通和比较的研究视角，为学生后续感悟大概念的意义相通性和运算一致性做好准备。

【教学片段二】探究算理，融入整体

1.独立研究

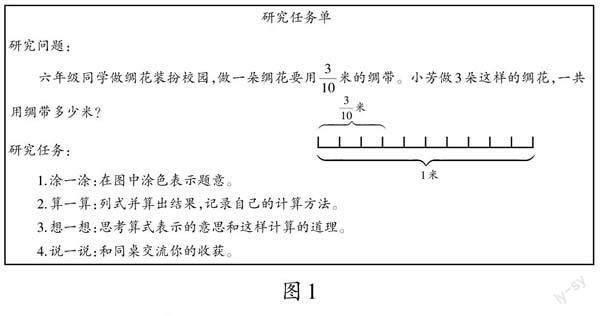
出示任务单（如图1）：

2.沟通比较

展示学生作品（如图2）：

师：你们真了不起，想出了这么多方法。老师注意到，虽然大家都算出了相同的结果，可列的算式不一样，都正确吗？为什么？

生1：正确。不管是加法还是乘法，都算出了做3朵绸花要用绸带的米数。

生2：正确。因为几个相同的数相加可以用乘法。

师：和我们学过的整数、小数乘法一样，几个相同的分数相加也可以用乘法计算。

师：你都能看懂这些方法吗？你看懂了哪个方法？

生3：第①个。每朵绸花用[3/10]米，3朵绸花就是3个[3/10]相加。

生4：第②个。他是将分数转化为小数来计算的。把新问题转化为已有知识来解决，是个好办法。

生5：第③个。他根据分数与除法的关系，把分数转化成整数来计算。

师：能看懂第④个的算法吗？

生6：根据乘法的意义，[3/10]×3就表示3个[3/10]相加，所以转化成连加来计算，这样同分母分数相加，分母不变，分子相加，分子3个3相加也可以写成3×3，所以结果是[9/10]。

……

师：这些方法之间有什么关系吗？

生7：①和④实质是一样的，都是计算3个[3/10]相加，只是分子的计算方法不同。

生8：②和③其實也是一样的，因为3÷10=0.3。

师：太棒了，你们不仅能理解这些方法，还能发现它们之间的联系。

【思考】布鲁纳在《教育的过程》中指出，一节课应该围绕社会认为值得人们持续关注的重大问题、原则和价值标准进行建构。鉴于此，本环节紧紧围绕“乘法意义的一致性”和“运算方法的相通性”这两个大概念进行整体建构。通过意义、算法和算理三个层次的沟通、比较，让学生自然地迁移乘法的意义，使分数乘法与整数、小数乘法的意义纵向贯通，并且展现算法多样化和算理沟通，使学生感悟到四则运算的关联性，深化对运算的整体认识。

【教学片段三】沟通算理，完善算法

师：请回忆我们是怎样计算整数乘整数、小数乘整数的。比一比，分数乘整数和它们一样吗？

生1：我觉得有不同的地方，也有相同的地方。相同的地方是它们都是先用整数相乘，不同的是算出的结果表示的数的大小不同。

生2：是一样的，就像生1说的，都是先计算出有多少个计数单位，整数、小数是计数单位，分数叫分数单位，再看结果是多少。

生3：都是先把数拆成计数单位和个数，算出个数再合成结果的。

师（根据学生的回答完成板书，如图3）：同学们真了不起，可以这么深刻地认识乘法运算的道理。

出示例题：小华做5朵这样的绸花，一共用彩带几分之几米？在作业纸上列式并解答。（学生独立完成后全班交流）

……

师：面对能约分的分数乘法算式，先约分再计算更简单。对照刚才计算的这些算式，说一说分数和整数相乘时可以怎样计算？

生4：分子与整数相乘，算出分数单位的个数，分母不变，能约分的先约分再计算。

【思考】本环节重在对分数和整数、小数乘法算理一致性的建构和分数乘法算法的归纳。出示算式资源，引导学生在讨论中体会乘法算理的一致性——都是计数单位个数的累加，计算时都是先计算有多少个计数单位（分数单位），再根据位值制表示结果。在此基础上，通过比较计算过程让学生明确能约分的先约分，为后面再次完善算理一致性的整体建构留下即插“接口”。

【教学片段四】实践应用，深化整体

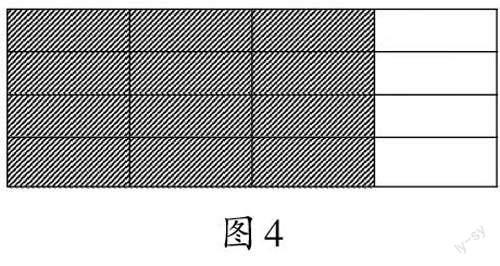
师：刚才我们一起研究了分数与整数相乘，下面就运用学到的知识解决一些实际问题。先在长方形中涂出4个[3/16]，再算出涂色部分一共是这个长方形的几分之几。

生1：我是竖着涂出4个[3/16]，结果是[3/4]。（如图4）

生2：我是横着涂出4个[3/16]，结果也是[3/4]。（如图5）

师：不管怎样涂，从图上都可以看出，涂色部分都是长方形的[3/4]。

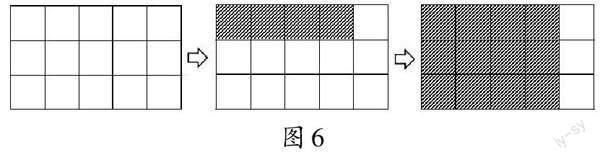
师：图形里藏着的数学奥妙不止这些，我们接着看。观察图示变化，先写出算式，再说一说算式表示的意思。（动态出示图6）

生3：算式是[4/15]×3，它表示3个[4/15]相加。

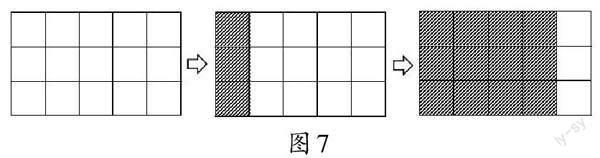
师：你们都是这么想的？再看一题。（出示图7）

生4：[3/15]×4，表示4个[3/15]相加。

师：你有什么发现？

生5：图示的过程不同，算式也不同，最终的样子是相同的。

生6：算式不同，表示的意义也不同，它们的结果是相同的。

师：为什么会这样？

生7：因为不管是[4/15]×3，还是[3/15]×4，都是用3×4算出12个[1/15]，结果是一样的。

师：[3/10] ×3可以解决生活中的什么问题？请编一个用[3/10]×3解决的实际问题。

出示信息：

（1）每袋面包[3/10]千克，3袋面包共多少千克？

（2）一个蛋糕，小芳和爸爸妈妈分别吃了它的[3/10]，他们一共吃了这个蛋糕的几分之几？

（3）一根彩带长3米，用掉它的[3/10]，是用掉了多少米？

（4）一块花田3公顷，其中的[3/10]种玫瑰，种玫瑰的面积是多少？

师：这些问题也能用[3/10]×3来解决吗？结合题目说一说，[3/10]×3分别表示什么意思，你有什么发现？

生8：前面两道题的是表示3个[3/10]相加的和，或者说是[3/10]的3倍是多少。

生9：后面两道题的都表示求3的[3/10]是多少。

师：同样是[3/10]×3，但表示的意义不同，这两种意义是不是相通的呢？我们下节课接着研究。

【思考】前面三个教学片段是对乘法的意义和运算的一致性进行了纵向贯通，为整数、小数和分数的乘法运算之间建立连接。而分数乘法还有其特殊性，即可以表示“一个数的几分之几是多少”這个意义，教学片段四就是要进一步完善分数乘法的整体架构：首先通过涂色表示算式，帮助学生巩固分子与整数相乘时先约分再计算的道理；然后设计一道逆向思维练习——看图示变化列算式说意义，深化学生对运算一致性的认识；最后，要求学生根据算式创编实际问题，学生通过分析数量关系，发现“即使算式相同，表示的意义也有变化”，感受到分数乘法还可以表示一个数的几分之几是多少，向后续学习延伸。

总之，整节课教学在“乘法运算”主题下，依托乘法意义一致性和乘法运算一致性等大概念，实现了整数、小数和分数乘法的纵横贯通，促使学生从整体的视角理解和掌握分数与整数相乘的意义与方法。在更大的“数与运算”主题下，学生感悟到了四则运算本质上的一致性——计数单位多少的累积与表达。在这样的教学探索中，“分数乘法”单元不再只有分数的运算、乘法的“小整体”，还具有了数与运算的“大整体”。由此，单元联结着课程与课时，单元教学的整体性思维与构型一定程度上就是课程学习的整体性样态与进程，教师建构单元整体时要解构表面的单元课时内容之间的“小关联”，依托更上位的主题大概念，从知识发展脉络和学习本质内核上重新定位“大目标”、设计“大活动”、建立“单元链”，为学生核心素养的发展预留更多“大接口”。

［ 参 考 文 献 ］

[1] 马云鹏.“深度学习”视域下的小学“数的运算”教学[J].福建教育，2020（36）：26-31.

【本文系2022年度江苏高校哲学社会科学研究重大项目“大概念的教学意蕴与统摄机制研究”（编号：2022SJZD0

44）和2022年江苏省研究生教育教学改革一般课题“大概念视域下小学教育专业硕士教学想象力生长路径研究”（编号：JGKT22_C082）基金项目的研究成果。】

（责编 金 铃）