冷轧变形抗力智能算法模型研究

肖保树,沈至諴

(上海宝信软件股份有限公司,上海 201900)

1 概述

冷轧带钢塑性变形抗力的预报精度直接影响到轧制力、前滑等轧制模型的设定精度。为了准确预测冷轧带钢的塑性变形抗力,提高轧制模型的设定精度,需要建立冷轧变形抗力预测模型。影响带钢的塑性变形抗力的因素包括:①来料化学成分;②热轧终轧温度/卷取温度[1];③冷轧各个机架的累积压下量;④轧制速度。传统变形抗力预测采用曲线拟合的方式建立模型,由于上游机组工况的变化,该模型不能自学习,因此精度不高,需要工艺人员不断进行离线优化来保证设定值精度。

随着深度神经网络学习算法研究在工业领域应用的逐渐成熟,深度神经网络算法具备非线性映射能力,不需要精确的数学模型,擅长从给定的学习样本数据中,模仿生物神经系统建立网络模型[2]。本文基于深度神经网络学习算法研究建立冷轧变形抗力预测模型,并在某钢厂冷连轧机组中成功应用,取得了良好的效果。

建立基于智能算法模型的基础是需要对变形抗力参数的影响因素进行数据分析,并收集历史参数作为智能算法模型的训练样本和测试样本。训练完成的智能模型才能够作为在线模型投入使用。在实际使用过程中,该智能模型还具备自学习功能。由于工业生产现场存在大量的重复数据,而且还会不定时增加新的钢种规格数据,只有具备自学习功能的模型才能够满足现场不断变化的生产需求。图1为建立该冷轧变形抗力参数自学习模型的流程图。

图1 变形抗力参数自学习模型流程图

2 传统的拟合算法

变形抗力是材料在压力加工时由于拉伸变形产生的强度。在冷轧轧制模型计算中,变形抗力在轧制力和前滑计算中起重要的作用,因此如何准确计算材料的变形抗力十分重要[3-5]。传统的材料变形抗力是通过拉伸试验得到的,通过给定带钢在不同的塑性变形量且不致破坏的条件下,测量带钢在不同变形量下的屈服强度。根据测量的屈服强度参数采用拟合方式近似得到变形抗力计算模型,如表1所示。

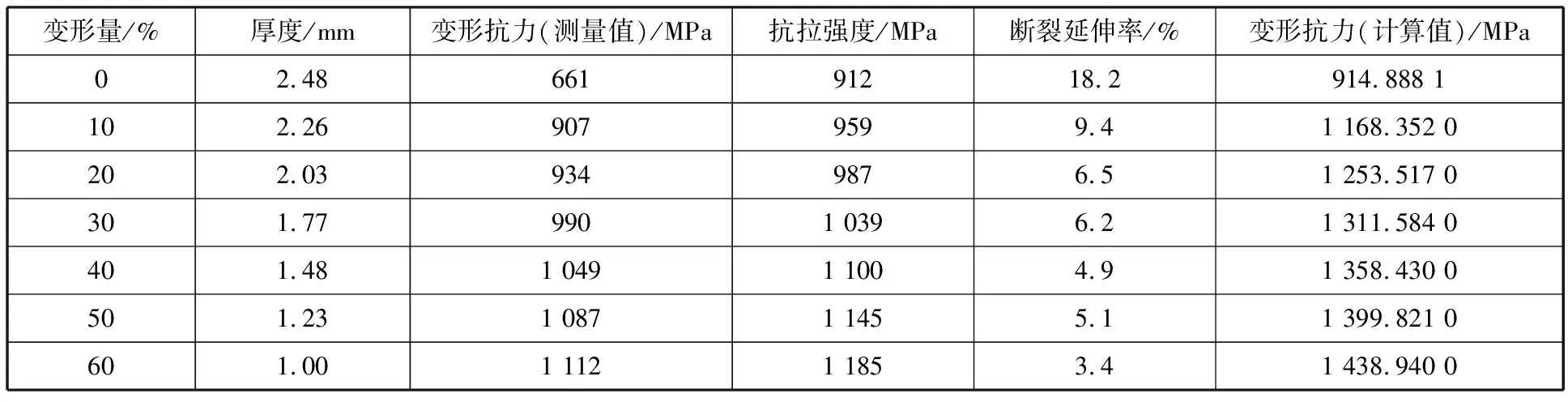
表1 某QP钢种变形抗力测试数据

由表1可以得知,带钢的变形抗力和变形程度有关,其曲线在轧制模型中是采用拟合方式来近似的,公式如式(1):

k=l(ε+m)n

(1)

式中:k为带钢的变形抗力;ε=ln{H/h}为带钢在某个机架的变形程度,H为某机架入口厚度,h为某机架出口厚度;l、m、n分别为计算变形抗力的3个拟合系数,其结果需要人工干预进行调整。

从表1中可以看到,变形抗力的测量值和计算值偏差较大。因此在实际生产现场,往往需要工艺人员根据实际轧制的状态优化不同钢种的变形抗力参数。

3 深度神经网络算法模型

本研究中神经网络的实现基于开源TensorFlow深度学习平台框架和Keras神经网络算法库,输入参数为带钢的化学成分、热轧终轧温度、卷取温度、钢卷厚度、钢卷宽度、速度,输出参数为变形抗力参数。在神经网络的回归过程中,利用初始随机权重和偏差,计算输出并与变量的实际值进行比较。如果误差超过目标最小值,权重和偏差再次更新和训练,同步多次重复该过程,直到获得隐藏层中给定数量的节点的最佳性能。

3.1 数据收集及处理

收集冷连轧机组的历史数据,包括带钢的钢种、规格、化学成分、热轧终轧温度、热轧卷取温度、各个机架的轧制力、各个机架的张力、各个机架的带钢速度、各个机架的轧辊辊径等数据,一共使用了7 161卷带钢数据。利用皮尔逊相关系数法对上述的各项输入参数与变形抗力参数进行分析,计算得到的相关系数矩阵如表2所示,其结果在[-1,1]之间,绝对值越大则相关性越强,绝对值越小则相关性越弱。由此可知,带钢的化学成分(主要为C、Si、Mn、N等元素)、热轧终轧温度、卷取温度的相关性绝对值超过0.2。为简化模型的输入维度、降低其复杂性、防止模型过拟合,可以适当减少相关性较小数据,因此将它们作为输入参数用于神经网络深度学习。

表2 各类参数与变形抗力系数的相关性强弱

模型的输出参数是变形抗力模型参数l、m、n。

首先需要根据各个机架的实际轧制数据计算出各个机架的带钢实际变形抗力,然后根据每个机架的变形抗力参数计算出变形抗力模型的参数l_a、m_a、n_a。

这里采用单纯形法求解这三个参数。

令初始修正系数alpha的范围alpha1=0.56≤alpha≤alpha2=1.668,读取人工经验数据得到初始化变形抗力模型参数:msl=l、msm=m、msn=n。然后利用二分法求出第i个机架的修正系数alphai,使得模型利用alphai修正的变形抗力参数msli=l×alphai、msmi=m、msni=n所求得的轧制力Fri与实际轧制力Fr_tari的误差Fr_erri=Fr_tari-Fri=0。

利用公式(1)给出的计算变形抗力的方法可知ms_tari=alpha×l(ε+m)n。

构建以msl、msm、msn为坐标的3维空间3+1=4个顶点Pn,n=1,2,3,4的初始单纯形。其中,

P1={min_msl,min_msn,min_msm}

P2={min_msl,max_msn,max_msm}

P3={max_msl,min_msn,max_msm}

P4={max_msl,max_msn,min_msm}

(2)

在该应用中,f(Pi)为Pi中的坐标利用公式(1)计算所得的变形抗力msi与ms_tari的平方误差和err。具体公式如式(3):

weight×(msn-ms_tarn)2

(3)

式中:msi是第i机架的变形抗力;n为机架个数;weight为末机架的平方误差权重。

利用式(2)中获得的初始单纯形即可按照上述原理步骤进行计算,经过反射、延伸、收缩、压缩,直至|f(PH)-f(PL)|<ε,直至ε<10-8。记此时的最优解为PL1,函数值为f(PL1)。

接着构建初始单纯形,令:

P1={min_msl,min_msn,max_msm}

P2={min_msl,max_msn,min_msm}

P3={max_msl,min_msn,min_msm}

P4={max_msl,max_msn,max_msm}

(4)

可得最优解PL2及其函数值f(PL2)。

接着令:

P1={PL1→msl,PL1→msn,PL1→msm}

P2={PL1→msl×1.09,PL1→msn,PL1→msm}

P3={PL1→msl,PL1→msn×1.09,PL1→msm}

P4={PL1→msl,PL1→msn,max_msm}

(5)

可得最优解PL3及其函数值f(PL3)。

比较函数值f(PL1)、f(PL2)、f(PL3),取其中的最小值对应的坐标PLi作为最终优化的变形抗力参数l_a、m_a、n_a。

3.2 样本集的构建

对于全部钢种数据,经过整理,输入参数为9个相关性较高的化学成分(C、Si、Mn、P、S、Cr、Nb、Ti、N)及带钢的终轧温度(FCTM)和热轧卷取温度(HCTM),共11个变量。针对每一个钢卷数据进行标记,选取其中的11个变量参数。

输出参数为利用3.1中单纯形法回归所得的变形抗力参数l_a、n_a,而m_a的值相对固定,其值接近0.01,没有预测的必要。

为了消除每个参数之间的单位不同的问题,对这些输入进行了归一化处理,归一化公式见式(6):

(6)

最终的输入是化学成分与热轧终轧温度、热轧卷取温度,输出是变形抗力参数中的L和N两个决定性参数。

3.3 构建模型

变形抗力参数自学习模型的本质是一种数据回归问题,根据已知的影响因素x,预测变形抗力参数y。本研究采用了有监督的神经网络学习算法,基于开源TensorFlow深度学习平台框架,采用Keras神经网络算法库,构建变形抗力自学习模型。

以下是模型的部分代码:

#导入模型

model = Sequential()

# 输入层

model.add(Dense(units=32,activation=‘relu’,input_shape=(X_train.shape[1],)))

# 丢弃神经元链接概率

model.add(Dropout(0.1))

# 中间层全连接激励函数relu

model.add(Dense(units=32,kernel_regularizer=regularizers.l2(0.01),activation=‘relu’))

# 输出层用线性

model.add(Dense(units=2,activation=‘linear’))

history=model.fit(X_train,y_train,epochs=300,batch_size=200,verbose=2,

validation_data=(X_test,y_test))

#保存模型

model.save(‘sks.h5’)

3.4 预测结果

随机将数据集分割成80%的训练集和20%的测试集。

表3为测试集中的几个典型的钢种在利用深度学习后预测的变形抗力参数和实际变形抗力参数之间的对比。

表3 典型钢种的预测和实际结果对比

表4为预测结果在利用决定系数R2、平均绝对误差MAE和均方根误差RMSE计算所得的分数。其中,R2越大代表模型效果越好,最大值为1;MAE和RMSE越小则代表模型误差越小。

表4 预测结果的得分

可以看出,在确定来料的化学成分和热轧卷取和终轧温度以后,模型即可给出相当可靠的预测结果。

3.5 模型应用效果

该变形抗力参数自学习模型在某钢厂冷连轧机组投入在线,通过对轧制数据进行分析,针对同种规格分别采用原始变形抗力参数计算设定值和采用神经网络自学习模型预测的变形抗力参数卷设定值,对比设定轧制力和实际轧制力。轧制力自适应系数是实际轧制力与设定轧制力的比值,当比值接近1时,说明设定轧制力和实际轧制力是吻合的。表5是自学习投入前后轧制力自适应系数对比,现场一共统计分析了9个钢种,1 131个不同规格设定值参数。经过对1 131个不同钢种规格的钢卷数据进行对比,采用初始变形抗力参数计算的轧制力精度是1.015,采用自学习之后的变形抗力参数计算的轧制力精度是0.995。

表5 自学习投入前后轧制力自适应系数对比

从以上数据可知,投入变形抗力参数智能自学习模型之后,设定值精度平均提升了1%。

4 结论

(1)根据实验室拉伸试验得到的变形抗力数据和实际轧制设定计算的变形抗力数据偏差较大,需要有经验的工艺人员在模型系统中不断维护变形抗力模型参数。

(2)根据实际变形抗力通过构建单纯形法计算变形抗力参数曲线,是建立智能变形抗力参数模型的基础。

(3)采用变形抗力参数智能自学习模型之后,冷连轧机组轧制力设定值精度较传统模型参数计算精度提升了1%。

(4)根据实际数据利用单纯形法计算变形抗力参数曲线,自动计算现有钢种的变形抗力参数,可以极大减少人工对现有钢种变形抗力参数表的数据更新,使其更符合实际轧制参数。对于化学成分、热轧终轧温度等改变的钢种或未在某机组轧制过的新钢种,在采用智能自学习模型计算以后,可以预先得出该钢种较为精确的变形抗力参数曲线,在首次模型计算中,能够更加吻合该机组的轧制参数,并在之后的生产中不断自我优化。