基于承载能力和传动效率优化的机器人RV 减速器摆线轮齿廓修形影响研究＊

王春光 罗志江 张俊峰

（①广东工业大学机电工程学院，广东 广州 510006；重庆电子工程职业学院智能制造学院，重庆 401331）

RV 减速器具有传动比范围大、传动精度高、承载能力强、传动平稳和传动效率高等诸多优点。作为工业机器人最为核心的部件之一，它一般安装在工业机器人的底座、大臂等重负载区域。RV 减速器结构复杂，技术壁垒高，在复杂约束条件下，尤其是考虑齿廓修形的情况下，进行RV 减速器结构精确设计是一个迫切需要解决的问题。因此，开展RV 减速器结构优化设计方法研究，对于提高RV 减速器整机性能具有重要意义。

RV 减速器摆线轮齿廓修形直接影响RV 减速器的传动精度、承载能力和效率等传动性能[1-2]。为了提高RV 减速器的传动特性，摆线轮齿廓修形必须选择合理的修形方法及严格控制修形量。陆龙生等结合传统等距修形方法和移距修形方法，提出了一种基于优化承载能力的RV 减速器摆线轮齿廓的新型等距-移距组合修形方法[3]。安宗文等为合理选择修形方法及修形参数、改善摆线轮齿面的受力状态，提出了一种以优化承载能力为目标、基于粒子群优化算法的摆线轮齿廓等距-移距修形方法[4]。以上两种方法的优化变量只考虑了等距和移距修形量两个变量，以承载能力为单一优化目标，优化变量和优化目标难以全面地体现RV 减速器的运动特性。

为了提高RV 减速器的使用性能，国内外众多学者对RV 减速器的优化设计方法进行了研究。刘江等对RV 减速器的传动精度进行了可靠性分析和优化设计，采用多目标遗传算法，以摆线针轮最大磨损和最低加工成本为目标对摆线针轮及其他关键零件的参数进行优化分析[5]。Yang M D 等将改进后的先进均值法和Double-Loop 法相结合，建立了RV 减速器优化模型，基于不同程度的可靠性，对减速器的体积进行了优化[6]。余永康等使用Romax Designer 软件和遗传算法对RV 减速器承载能力和传动误差进行了修行优化[7]。王明楠等使用拓扑优化的方法来对RV 减速器的针齿壳和行星架进行了轻量化设计，在保证强度足够的情况下减轻了整机的质量[8]。郑胜予等基于NSGA-Ⅱ遗传算法，以体积最小和可靠度最高为目标对摆线针轮行星减速器进行了优化[9]。楼嘉彬等基于遗传算法对RV 减速器摆线针轮结构进行了可靠性优化[10]。由上述研究可见，目前RV 减速器的优化设计主要涉及体积、轻量化、可靠度、承载能力和传动精度等方面，而承载能力和传动效率是RV 减速器的核心指标，把传动效率和承载能力有效结合起来进行多目标优化更有益于RV 减速器的精确设计。

本次以RV-40E 减速器为实例，以关键设计参数作为设计变量，考虑摆线轮齿廓修形影响，以摆线针轮最大啮合力最小和整机传动效率最高为优化目标进行多目标优化，并结合TOPSIS 和CRITIC方法确定Pareto 解集中的最优解，采用NSGA-Ⅱ遗传算法和动态仿真来进行求解和辅助验证，力求提高整机的承载能力和传动效率。

1 RV 减速器结构优化模型

RV 减速机由一级行星齿轮机构和二级摆线针轮减速机构组成，一级减速机构是由中心轮和行星轮构成的行星齿轮传动系统，二级是由曲柄轴、摆线轮、针齿和行星架构成的传动系统，其机构简图如图1 所示[11]，二级减速机构的减速比远大于一级减速机构[12]。

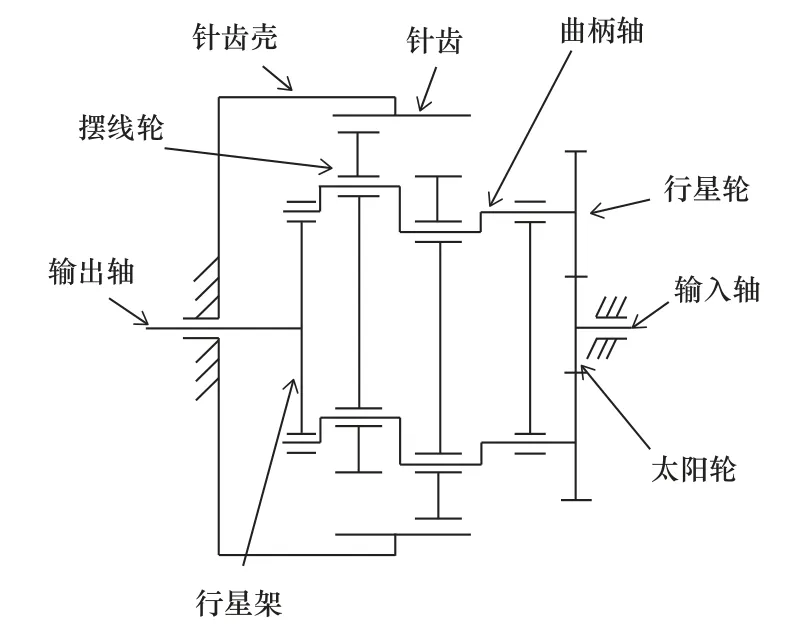
图1 RV 减速器机构简图

1.1 目标函数

1.1.1 传动效率

RV 减速器整机传动效率为

式中：x取值为1 或-1[14]，当时，x=1；当时，取x=-1。RV 减速器传动比一般比较大，所以为原始机构的传动效率，。其中：；fz是指齿轮啮合摩擦系数，一般取0.035[15]；n为行星轮的数目，本文以RV-40E 减速器为例，n取2。

式中：Kz=3-2K1，K1为短副系数。

将式（3）和式（4）代入式（1），可得：

因此RV 减速器传动效率目标函数为

1.1.2 承载能力

针对RV 减速器承载能力的优化，以减少针齿的最大承载能力为目标[16]，摆线针轮的最大啮合力Fmax是决定承载能力的主要因素。

计算摆线针轮的最大啮合力的步骤如下。

（1）计算每个啮合点处法向方向的初始间隙[17]。

式中：∆rrp为等距修形量；∆rp为移距修形量；ϕi为第i个针齿相对于转臂的转角，即ϕi=360/(Zd+1)，当ϕi=arccosK1时，此处的轮齿受力最大[18]。

（2）每个啮合点处的法向总位移δi[19]。

式中：δmax为受力最大的一对齿的总变形量[19]；wmax为接触变形；fmax为针销弯曲变形。

式中：B的取值，二支点针齿销为31/64，三支点针齿销为7/128[20]；L为针齿销的长度，值为L=2b；E为弹性模量，取E=2.06×105MPa[21]；u为泊松比，取u=0.3[22]；Fmax为受力最大一对齿的啮合力。其中 ρc的公式为[23]

（3）计算同时啮合的齿数。

将 ∆ϕi和 δi进行比较。满足公式（12）的轮齿都进入啮合状态。

（4）摆线针轮的最大啮合力计算[24]。

式中：T为负载转矩；为摆线轮节圆半径,；n,m表示第n个齿到第m个齿是同时啮合的；li为第i个针齿的力臂，公式如下[26]。

求Fmax需要先求δmax，而求δmax需要计算Fmax，因此需要赋予最大啮合力初始值。变量参数每一次迭代更新，都需重复一次最大啮合力计算过程，直到设置的最大迭代次数为止。

摆线针轮啮合力初始值F0为[27]

因此RV 减速器承载能力优化的目标函数为

综上所述，可以得出RV 减速器多目标优化目标函数为

1.2 设计参数

针对RV 减速器传动效率和承载能力的优化，除需考虑摆线修形涉及的参数之外，还需要考虑其他有关设计参数。从传动效率公式（5）和最大啮合力计算公式（13）来看，与优化目标相关的设计参数包括：短幅系数K1、太阳轮齿数Zs、针齿半径rrp、摆线轮厚度b、移距修形量∆rp、等距修形量∆rrp、摆线轮齿数Zd和针齿中心圆半径rp。

将参数表示为如下向量形式：

1.3 约束条件的建立

（1）针轮中心圆半径rp。

为了防止优化过程中RV 减速器的体积变化太大，需要对rp进行约束[28]。根据经验公式rp=，可得约束条件为

（2）摆线针轮啮合不顶切。

为了使摆线针轮齿廓不发生尖角和顶切，摆线轮理论齿廓曲率半径系数的最小值amin必须大于针齿套半径与针轮中心圆半径的比值[3]，即amin>rtp/rp，而amin=(1+K1)2/(1+K1+K1Zd)，因此约束条件为

式中：rtp为针齿套半径，因为RV-40E 针齿套半径较小，所以和针齿做成一体，即rtp≈rrp。

（3）针径系数K2。

K2影响了针齿分布的疏密程度，本文以RV-40E 减速器为例，针轮齿数在40 左右，所以K2比较合理的取值范围为1.1～1.8[29]。

则针径系数K2的约束条件为

（4）短副系数K1。

短副系数K1影响摆线轮的齿廓曲线和承载能力、减速器传动的性能以及是否会发生顶切。RV-40E减速器的摆线轮齿数一般在25～59，因此K1的合理取值在0.65～0.9[30]。得到短副系数K1的约束条件为

（5）摆线轮厚度。

摆线轮厚度b一般按照（0.1～0.2）rp来取值[31]，因此摆线轮厚度的约束条件为

（6）最大接触应力。

由赫兹接触理论可得[32]：

式中：Ee为当量弹性模量，由于摆线针轮的弹性模量一样，Ee=E=2.06×105MPa；摆线针轮的材料是GCr15，σHP一般取1 300～1 500 MPa 比较适宜[33]。

（7）等距和移距修形量。

为了防止等距修形量过大而导致降低RV 减速器的传动精度和同时啮合齿数，需要对等距和移距修形量进行约束[21]。

2 基于TOPSIS 和CRITIC 相结合的多目标决策

CRITIC 权重法是基于判断指标间的变异性和冲突性的综合衡量来进行权重赋予，这符合RV 减速器承载能力和传动效率之间相互矛盾的性质。TOPSIS 法是通过欧式距离评判各方案的优劣[34]。将TOPSIS 法和CRITIC 法相结合可以避免TOPSIS法权重一致性问题，最终得到的结果也更为客观和符合RV 减速器实际情况。

设有n个评判对象，即Pareto 前沿分布图中的点数和m个判断指标，即优化目标个数，通过两者可构造一个判断矩阵M：

式中：vij为第i个评价对象第j个判断指标。为了进行后续的处理，将极大型数据（极值越大越佳）和极小型数据（极值越小越佳），将这两种数据进行正向化处理，正向化的公式如下[35]。

极大值数据正向化：

极小值数据正向化：

为了消除判断指标之间不同量纲的影响，需要对正向化后的矩阵进行标准化，即用正向化矩阵中的每一个元素除以其所在列的元素的平方和的开平方，公式如下：

实际中需要判断指标应有的权重，因此需要对权重进行重新赋予。其中变异性和冲突性分别以标准差和相关系数的形式来表现。

冲突性系数Rj公式如下所示[36]，其中Cij为判断指标j和评判对象i之间的相关系数。

权重Wj见式（38）[36]，显然越大，判断指标分配的权重也就越大，说明第j个指标在整个系统中的重要性越大。

对象评价得分计算公式如下：

评价得分最大的对象即为最优解。结合TOPSIS 和CRITIC 权重法来对RV 减速器的多目标优化结果来进行多目标决策，可以客观地从Pareto最优解集中选出最优解。

3 实例优化

以广泛应用于工业机器人领域的RV-40E 减速器为例，传动比121，输出转矩T1=307 000 N·mm，输入转速n0=40×121 r/min，输入转矩T0=2 918.66 N·mm。使用NSGA-Ⅱ多目标遗传算法进行计算，设置初始种群大小为200，迭代次数为1 200，变异率为0.1，交叉率为0.9。

3.1 齿廓修形对优化目标的影响

当齿廓修形作为变量时，仿真计算得到Pareto前沿分布如图2 所示，横坐标是目标函数minf1(x)，即1 减去RV 减速器传动效率，纵坐标是minf2(x)，即摆线针轮的最大啮合力Fmax。

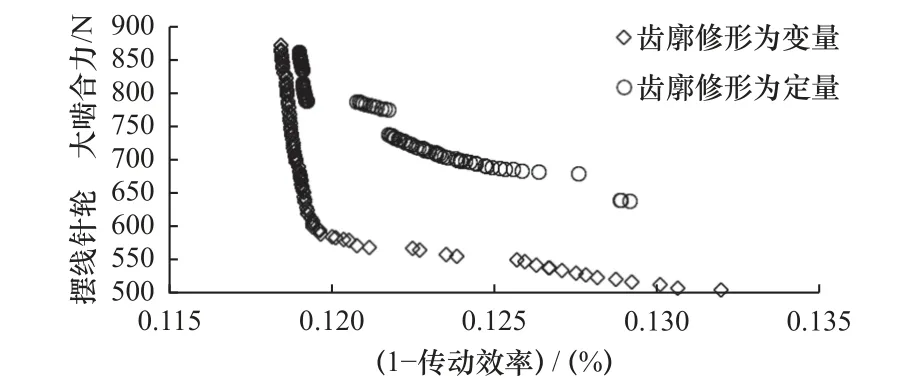
图2 Pareto 前沿分布

由图2 可知，齿廓修形对RV 减速器的传动效率影响较小，对摆线针轮啮合力影响较大。

当采用正等距或者负移距时，齿廓修形对啮合力的影响如图3 所示。

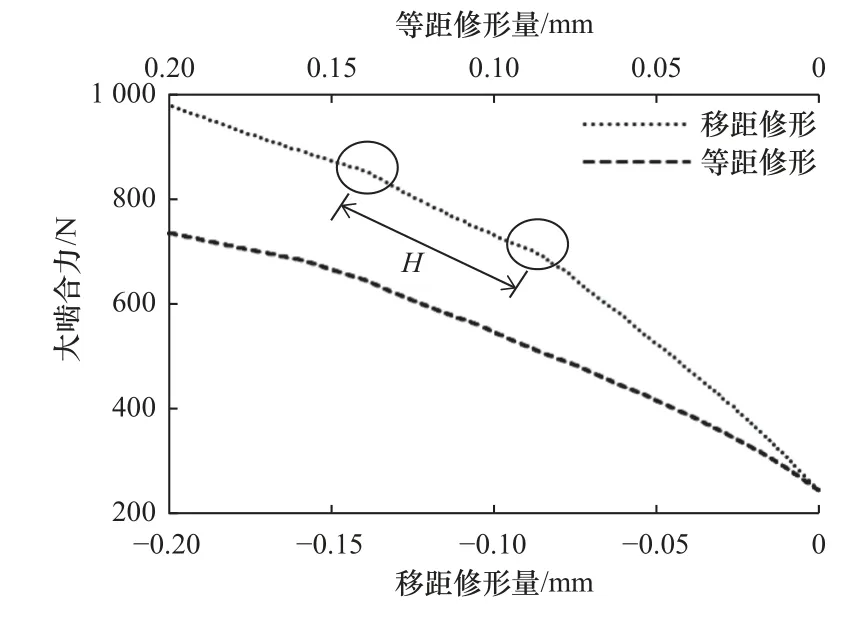
图3 等距修形或移距修形对啮合力的影响

由图3 可知：

（1）相同的修形量情况下，负移距修形对啮合力的影响比正等距修形显著。

（2）图中两曲线的每一个拐点代表了同时啮合齿数的变化节点，即图中H区间的同时啮合齿数是相同的。随着修形量增大，H区间不断增大，修形对啮合力的影响也逐渐减小。

当采用“移距–等距”时，齿廓修形对啮合力的影响如图4 所示。

图4 “移距–等距”修形对啮合力的影响

由图4 可知：

（1）图中的拐点均代表同时啮合齿数的变化节点，在相同啮合力的情况下，随着等距修形量变化，曲线的拐点向着负移距修形量减小的方向平移。即等距修形可以提高移距修形对摆线针轮最大啮合力的影响程度。因此，采用等距–移距的组合修形方法对优化效果的影响更为显著，能以更小的修形量来降低啮合力。

（2）“负移距–负等距”和“正移距–正等距”可以找到啮合力的最低点，即每条曲线的转折点，此时的轮廓接近摆线轮理想齿廓，啮合齿数接近一半。

（3）“负移距–正等距”或“正移距–负等距”修形的修形量对啮合力的影响相对于“负移距–负等距”和“正移距–正等距”较为平缓，齿廓修形设计更为容易。

3.2 最优化结果分析

RV 减速器的体积计算公式如下[37]：

式中：ba为行星轮厚度；Za为行星轮齿数；∆1为摆线轮之间的间隔。

在最优解范围内，体积、传动效率和摆线针轮最大啮合力的变化情况如图5 所示。

图5 体积、传动效率和最大啮合力变化

可见随着摆线针轮啮合力的减小，减速器的体积也具有减小的趋势，传动效率也会逐渐降低。当传动效率提高至88 %左右时，摆线针轮啮合力和整机体积上升得很快。

根据前述基于TOPSIS 和CRITIC 相结合的多目标决策方法可得到最优解为minf1(x)=0.1211，minf2(x)=570.1608。优化参数圆整后可得最优解为minf1(x)=0.1211，minf2(x)=572.3657。通过获取最优解相对应的各参数值，可得优化前后结果对比，见表1。

表1 优化前后结果对比表

由表1 可清晰得到，经过多目标优化后，RV减速器的传动效率提高了0.96%，摆线针轮传动的最大啮合力减小了321.927 N，同时啮合的齿数也从5 个齿增加到了9 个齿。

由表1 可以看出，原始实例采用的是正等距–正移距相结合的修形，而优化后采用的是正等距–负移距相结合的修形方式，与图4 得到了分析结论相符合。

4 动态仿真分析

4.1 参数化建模

摆线轮齿廓通用摆线轮齿廓方程为[38]

使用NX 软件得到图6 所示优化后的RV40 减速器传动部分三维模型装配图。

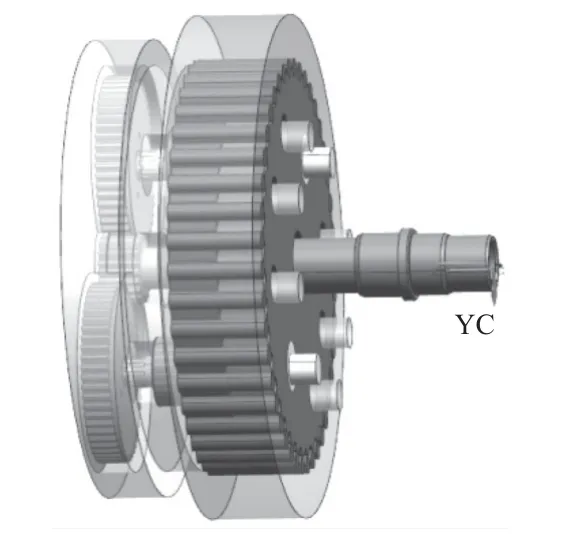
图6 RV40 减速器传动部分三维模型装配图

4.2 动态仿真分析

行星架质心角速度如图7 所示，可见行星架质心角速度在240°/s 上下波动，即输出转速n1=40 r/min，由上述已知输入转速n0为40×121 r/min，可得仿真模型的传动比为121，验证了RV 减速器的三维模型的正确性。

图7 行星架质心角速度

RV-40E 减速器优化前后摆线针轮啮合力变化如图8 所示，摆线轮的角速度为40 r/min，即1.5 s旋转一圈。可以看出优化前摆线针轮最大啮合力接近900 N，优化后摆线针轮最大啮合力为570 N 左右，验证了采用NSGA-Ⅱ遗传算法，以摆线针轮的最大啮合力Fmax最小和整机传动效率 η最高来进行多目标优化是可行的。

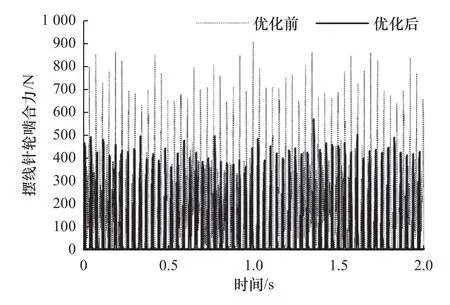
图8 优化前后摆线针轮啮合力仿真结果

行星架和摆线轮质心角加速度优化前后变化如图9 所示，曲线波动的幅值越大，能量损失越大。由图9 可以看出，优化后的行星架和摆线轮的质心角加速度曲线波动更小，整机的传动也更为平稳。

中心轮和行星轮质心角加速度优化前后变化如图10 所示，优化后的中心轮和行星轮的角加速度上下波动的幅值更小，啮合传动时的振动也会比优化前减小。

图10 优化前后中心轮和行星轮质心角加速度

5 结语

（1）提出一种基于承载能力和传动效率优化的RV 减速器摆线轮齿廓“负移距–正等距”或“正移距–负等距”的组合修形方法。建立了以承载能力和传动效率为优化目标的RV 减速器数学模型，使用NSGA-Ⅱ遗传算法以及TOPSIS 和CRITIC相结合的多目标决策方法求解得到了最佳优化方案。

（2）采用等距–移距的组合修形方法对优化效果的影响更为显著，能以更小的修形量来降低啮合力。

（3）“负移距–正等距”或“正移距–负等距”的修形量对啮合力的影响相对于“负移距–负等距”和“正移距–正等距”较为平缓，齿廓修形设计更为容易。

（4）使用NX 软件对RV 减速器进行参数化建模和动态仿真分析，结果发现摆线针轮最大啮合力的仿真结果与理论值基本吻合。通过分析优化前后行星架、摆线轮、中心轮和行星轮的角加速度发现优化后整机的传动更为平稳，动态性能得到了提升。