高速列车散热离心风机性能灵敏性分析及优化

屈小章 张加贝 翟方志

湖南联诚轨道装备有限公司,株洲,412001

0 引言

散热系统是保障高速列车安全运行的重要部件之一,主要用于牵引传动的变流器、变压器和牵引电机等产生热源的仪器和设备的冷却,离心风机是高速列车散热系统核心器件之一。在离心风机气动性能设计中,如何更好地匹配关键结构技术参数,提高风机的气动性能,满足工程应用要求,是工程设计人员的重要课题。近年来,国内外许多学者对风机气动性能做了一系列的研究。侯志泉等[1]利用三维雷诺平均N-S方程和SST湍流模型对斜流风机的内部流场和空气动力学性能进行了数值模拟,并通过试验进行了验证。迟劭卿等[2]通过试验和数值研究分析了进口条件对风机内部流量和风机墙性能的影响。刘刚等[3]采用大涡模拟(LES)结合声学模拟方程,研究了叶尖翅片对轴流风机的流场和声学场的影响。邢浩男等[4]以叶片安装角、叶片数、间隙占比为因素,设计了三因素三水平的Box-Behnken仿真试验,并对叶轮参数进行了优化。张立祥等[5]采用正交试验法设计试验,对叶轮的轮毂比、叶片数量、叶片安装角、叶片弦长、叶片扭转角和叶轮径向间隙6个主要结构参数进行优化改进和参数匹配,提高了矿用KJS-Y型降尘风机的除尘性能。姬成等[6]研究了非轴对称轮盘面对高压比离心叶轮的效率、压比、堵塞流量及工况范围的影响规律。李婧等[7]通过数值模拟分析了环形厚度、环形间距、环形数和环形内径等关键参数对流场和气动性能的影响。冀怡名等[8]利用LES方法和FW-H(Ffowcs Williams-Hawkings)方程建立了冷却风机的流场和噪声的计算模型。DING等[9]利用计算流体动力学(computational fluid dynamics,CFD)方法得到了离心风机的外部特性和叶轮、风机的内部特性。MANASERH等[10]建立了考虑不同风机工作环境的CFD模型,并进行了流场性能分析。LIU等[11]采用CFD方法对高海拔风机性能进行了模拟。

本文以高速列车散热系统的离心风机为研究对象,采用径向基神经网络(radial basis function neural network,RBFNN)学习模型,结合离心叶轮结构参数化模型,分别对离心风机气动性能进行单因素和多因素的灵敏性分析,识别了影响的关键参数,优化了离心风机气动性能。

1 气动性能分析模型及流程

1.1 离心叶轮结构参数化模型

离心风机叶轮结构参数有叶轮外径D2、叶轮进口直径D0、叶片进口直径D1、出口宽度b2、进口宽度b1、叶片出口安装角β2A、叶片进口安装角β1A、叶片数Z、叶片的圆弧半径Rk等。影响离心风机气动性能的关键参数如图1所示。

叶轮结构参数化模型数学表达式[12]如下:

(1)

(2)

叶片的弧长l为

(3)

(4)

1.2 CFD仿真模型

CFD领域中控制方程的求解仍然存在封闭方程的问题,这需要引入湍流模型[13]。RNGk-ε模型由重整化群方法导出[14],能调节湍流涡动黏度来考虑旋转效应的影响以及大尺度分离对壁面的影响。RNGk-ε模型[15]表达式如下:

(5)

(6)

式中,ρ为流体密度;ui为速度矢量;t为时间;ε为湍流耗散率;xi、xj为笛卡儿直角坐标;μeff为等效速度;k为湍流动能;Gk为平均速度梯度引起的湍流动能项;YM为可压缩湍流对总膨胀率的影响;Gb为浮力引起湍流动能k的产生项;C1ε、C2ε、C3ε为经验常数;αk、αε为湍流动能k和耗散率ε对应的Prandtl数;Sk、Sε为用户定义源项。

图2所示为离心风机结构几何简化模型和流场分析模型,离心风机原始模型可以在任意三维造型软件中创建。计算域分为三个部分,即进口、叶轮以及蜗壳,如图2b所示,其中进出口的长度可根据计算结果适当调整。建模时,叶轮转轴应和基准坐标轴共线,风机进口延长300 mm,风机整体宜采用四面体网格划分,对各流体域进行尺寸设置,对关键位置如叶片、进风道圆弧段以及蜗舌等重要部位进行加密。对于交界面,尽可能将交界面两侧网格设置成相同大小,或者上游网格尺寸小于下游网格尺寸。网格全部采用四面体网格,完成后对网格偏斜进行检查,最大偏斜小于 0.95,整体流体域的网格数约为230万。

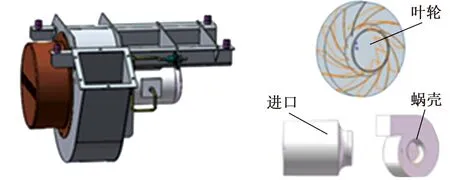
(a)结构模型 (b)简化模型

1.3 LHS模型

拉丁超立方采样法(Latin hypercube sampling,LHS)是一种随机抽样方法,主要用于优化设计、模型验证和参数估计等领域。LHS法在保持随机性的同时,能够有效避免重复样本和样本聚集的问题,从而提高了采样的效率和准确性,同时,它也可以应用于高维空间,保证每个维度上的样本点均匀分布。因此,高速列车散热系统的离心风机性能研究可以获得精度较好的采样空间及计算效率。LHS模型由抽样区间和相关性控制构成,矩阵ZN×n和RN×n为随机生成的标准正态样本点序列和所有标准正态样本点的排序信息,每个抽样的样本点的累积概率分布函数Fxj(Xij)为[16]

(7)

i=1,2,…,Nj=1,2,…,n

式中,rand(0,1)为[0,1]内任一的均匀分布随机数;Rij为随机生成的所有标准正态样本点的排序信息;n为整数。

通过概率变换为独立标准正态空间,得到的LHS抽样样本点ξij为

ξij=Φ-1(Fxj(Xij))

(8)

式中,Φ-1(·)为标准正态累积分布的逆函数。

1.4 RBFNN模型

RBFNN模型是一种经典的人工神经网络模型,它在模式识别、函数逼近和预测等领域具有广泛的应用。它不但具有较好的泛化能力,可以处理高维数据和复杂的非线性关系,而且RBFNN的训练过程相对简单且具有较快的收敛速度。同时,RBFNN还具备一定的容错性,对输入数据中的噪声和异常值具有一定的鲁棒性。因此,为了提高离心风机气动性能的计算效率,采用RBFNN对较小的数据样本进行学习。

RBFNN是一种基于径向基函数的线性叠加模型。两层正向神经网络[17]由具有径向基函数神经元的隐含层和具有线性神经元的输出层组成。隐含层是含有神经元的径向基函数层,节点函数通常为高斯函数。输出层是有神经元的线性层,节点函数通常是简单的线性函数。径向基函数神经网络[18]的f(a)数学表达式如下:

(9)

式中,wi(i=1,2,…,nt)为权重系数;nt为采样点数;Hi(r)为径向函数。

以采样点为中心,改变欧氏距离,径向函数响应为单调函数,其表达式为

Hi(r)=H(‖a-ai‖)

(10)

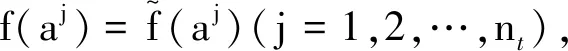
(11)

当函数H(a)是具有唯一解的正定函数且其采样点不重合时,可得到权向量系数,其矩阵表达式为

w=H-1F

(12)

F=(f(a1),f(a2),…,f(a(nt)))

将式(12)代入式(9)可得到预测域的近似值。

目前,学习模型的精度验证主要是基于方差分析,这种方法只适用于回归逼近方法,对于RBFNN模型,样本设计点的误差为0,不能使用方差分析。该学习模型的评价方法主要有交叉验证(CV)法。CV法是一种相对简单的模型评价和误差预测方法,其基本原理是将样本设计点分为两部分:构建子近似模型和评估子近似模型的精度。目前,该方法的参数评价主要采用均方误差(MSE)和预测残差平方和(PRESS)两种方法,表达式如下:

(13)

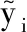
MSE和PRESS值越接近0,近似模型的拟合精度越高。

1.5 分析流程

基于神经网络学习模型的离心风机性能灵敏性分析及优化的分析过程如图3所示。

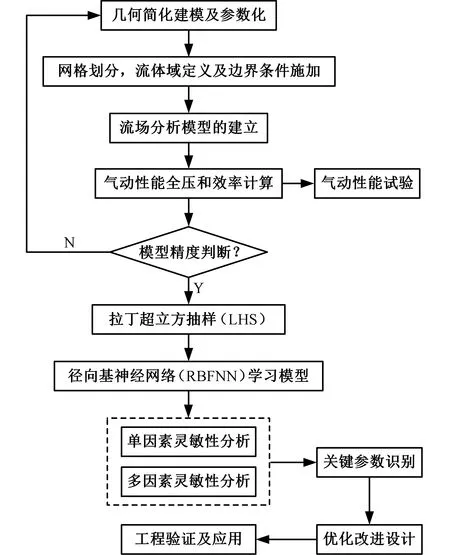
图3 气动性能灵敏性分析及优化过程

2 气动性能试验及结果对比

2.1 气动性能试验

为验证离心风机气动性能CFD计算模型的精度,按照GB/T1236—2000《工业风机用标准化风道进行性能试验》对离心风机气动性能进行试验,绘制它的流量、压力和效率等性能参数的特性曲线。

表征离心风机气动性能的主要参数有流量qV(m3/s)、全压Δp(Pa)、功率Pe(kW)、效率η(%)和转速n(r/min)。离心风机在单位时间内获得的有效功率Pe为[19]

(14)

效率反映了离心风机所做有效功的大小,可反映离心风机的气动性能,表达为

(15)

式中,Ps为轴功率。

采用U型管、皮托管和微压计来测试离心风机管路的动静压,使用节流锥调节气流流量,应用偏振测量仪(PAx1000)测试离心风机转速,采用电能质量分析仪(Fluck-43B)测试离心风机功率。离心风机气动性能试验装置如图4所示[19]。

图4 气动性能测试装置

风机性能测试主要步骤如下:

(1)对试验风机进行机械检查,目测装配、外观质量和安装尺寸是否符合要求,叶轮旋转方向是否准确。

(2)检查风机驱动电机的耐压和绝缘是否符合要求,准备相关仪器在测试平台上的安装和测试。试运转,确定风机运转方向是否准确,并将出口节流阀调至全开状态。

(3)启动风机,在风机处于全开位置下读取并记录试验数据,并逐渐调节出口节流口,使总压力逐渐增大,总压力增加到额定值前,试验3～4组数据;在接近总压力额定值时需试验1～2组数据;在高于总压额定值时试验2～3组数据。根据实际工程情况,一般需要6组以上的试验数据。

(4)对试验数据进行处理,得到风机的性能数据,绘制其性能曲线并分析。

在测试过程中,需要测试的性能参数主要包括电机参数、气动参数和环境参数。电机参数主要包括输入功率、转速和特性曲线。气动参数主要包括进出口静压、动压、速度等。环境参数主要包括空气湿度、试验室温度和大气压力等,这些参数对空气密度影响较大,对风机的压力有直接影响。通过对运行中的风机节流装置进行调节,可以得到不同工况下的试验数据。

为了分析试验误差对风机性能的不确定性,对样机进行多次重复试验,并对试验结果数据进行分析,挑选出三组全压Δp和效率η的边界数据(Δp1,Δp2,Δp3)和(η1,η2,η3),结果如表1和表2所示。表1是全压Δp与流量qV的试验结果,在工况点N=4处,最大误差E为3.01%;在工况点N=2处最大误差E为5.97%。表2是效率η与流量qV的试验结果,在工况点N=4处最大误差E为2.76%;在工况点N=7处最大误差E为5.96%。试验误差产生原因主要为试验人员在取试验数据时,由于数据跳动不稳定,存在较大差异,本试验采用了两个不同试验人员也会导致取数据的差异;同时试验设备本身存在标定误差,试验环境条件也存在一定差异。

表1 三次试验全压Δp与流量qV的试验结果

表2 三次试验效率η与流量qV的试验结果

2.2 计算结果与对比

离心风机的气流流量0.67 m3/s,叶轮的转速2910 r/min,静压为2625 Pa,采用不可压缩空气,空气密度 1.2 kg/m3,湍流黏度 1.79×10-5kg/(m·s)。边界条件为:进口施加不同工况的流量如表1所示,采用速度进口,压力出口,出口压力为0,边界条件施加如图5所示。

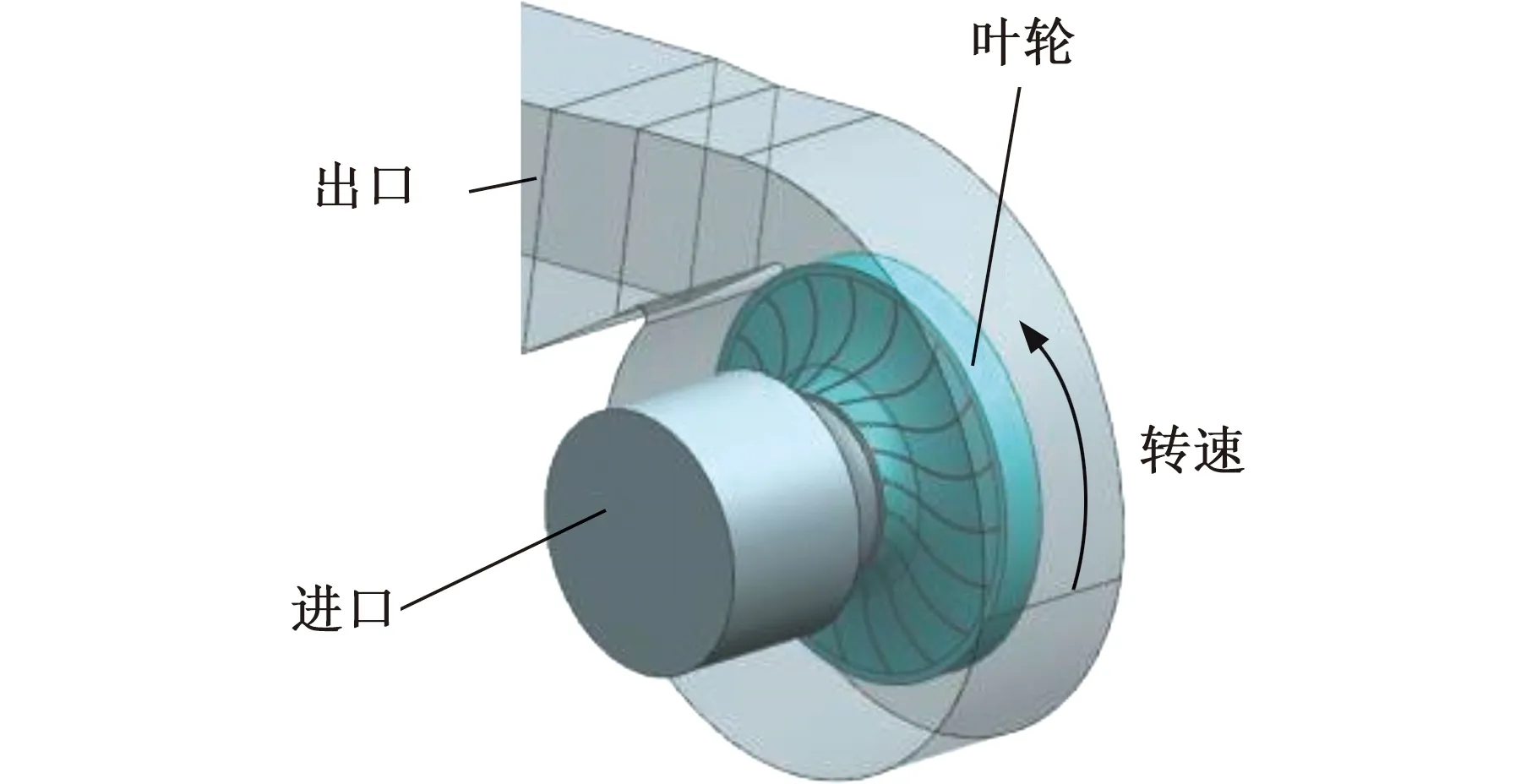
图5 边界条件

计算收敛后,根据对通风机总压及静压的定义,风机总压等于出口总压与进口总压的差值。计算得到风机气动性能结果如表3所示。

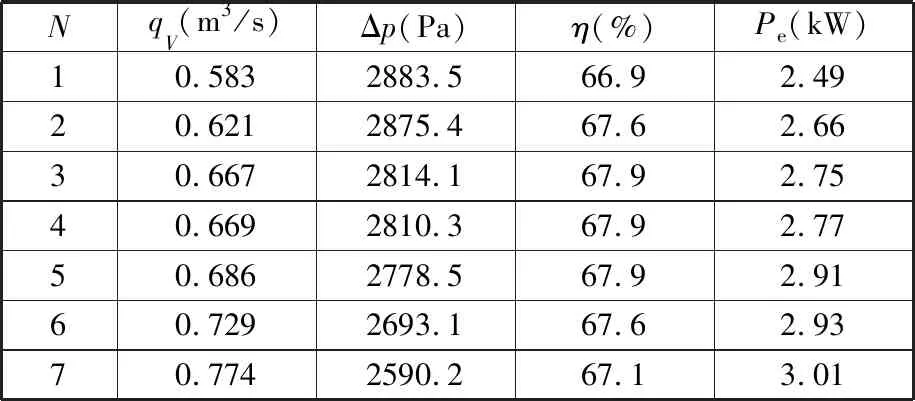
表3 气动性能计算结果

图6是离心风机工况点的流场云图。从图6a和图6b中分析,叶轮流场中存在明显的低速区和涡流现象,特别是在壁面处。

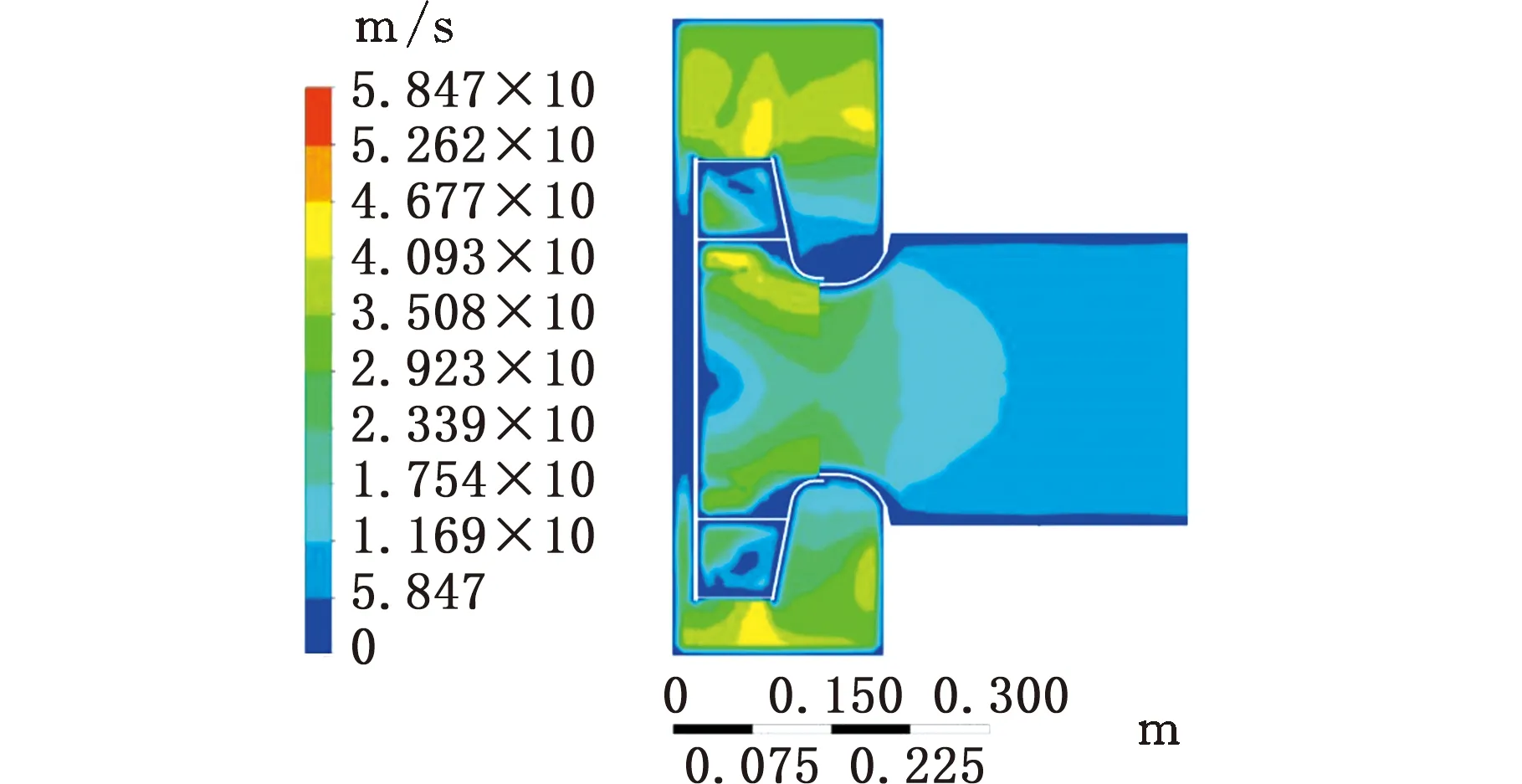
(a)整体速度分布

图7给出了计算值和试验值的对比情况,压力最大偏差为2.6%,效率最大偏差为5.9%。在工况点,压力误差为0.67%,效率为1.47%,根据表1和表2中样机试验误差结果,全压Δp和效率η均满足工况点误差3%和最大误差6%的要求,因此流场分析模型的精度可满足要求[19]。

(a)全压Δp与流量qV

计算值和试验值的误差主要来源于试验的工装和仪器测量的误差、离心风机成形和设计模型不一致性、试验环境和理想计算模型的差异性等。

3 气动性能灵敏性分析结果

3.1 单因素灵敏性分析结果

根据上文建立的风机气动性能CFD仿真模型,分析了叶片数Z和叶轮宽度b2对离心风机气动性能的影响,结果如图8所示。

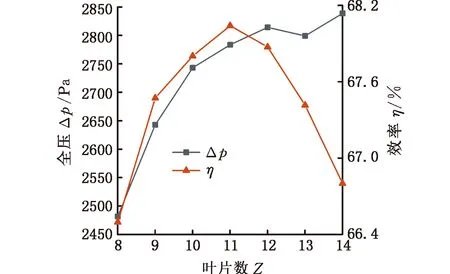
(a)叶片数Z的影响

由图8a可以分析出,随着叶片数的增多,全压Δp逐步增大,但当叶片数Z达到11及以上时,全压的变化不大。随着叶片数的增多,效率η先增大后减小,叶片数Z=11时的离心风机效率最高。因此,从上述分析可知,叶片数Z为11时,离心风机气动性能可达到最佳匹配。

由图8b可以分析出,叶轮宽度b2在67 mm时离心风机全压Δp最大;随着叶轮宽度b2的增大,离心风机效率η呈下降趋势,在叶轮宽度b2为65 mm时效率η最大。因此,要使离心风机效率η最高,可选用叶轮宽度b2为65 mm,要使离心风机全压Δp性能好,则可选用叶轮宽度b2为67 mm。

在图8b中,叶轮宽度b2对离心风机全压Δp和效率η的影响具有数据的波动趋势,是因为叶轮宽度b2主要影响离心风机流量qV,对全压Δp和效率η没有明显的规律影响。从数据分析可知,叶轮宽度b2对离心风机全压Δp虽有一定影响,但数据最大和最小差值仅有70 Pa,差值较小。效率η总体呈下降趋势与流体扰流影响有关。

3.2 多因素灵敏性分析结果

影响离心风机气动性能的结构参数还有很多,下面以叶轮进口直径D0、叶片进口直径D1、叶轮外径D2、叶片出口安装角β2A和叶片的圆弧半径Rk为多因数参数,采用LHS模型进行抽样,结果如表4所示。

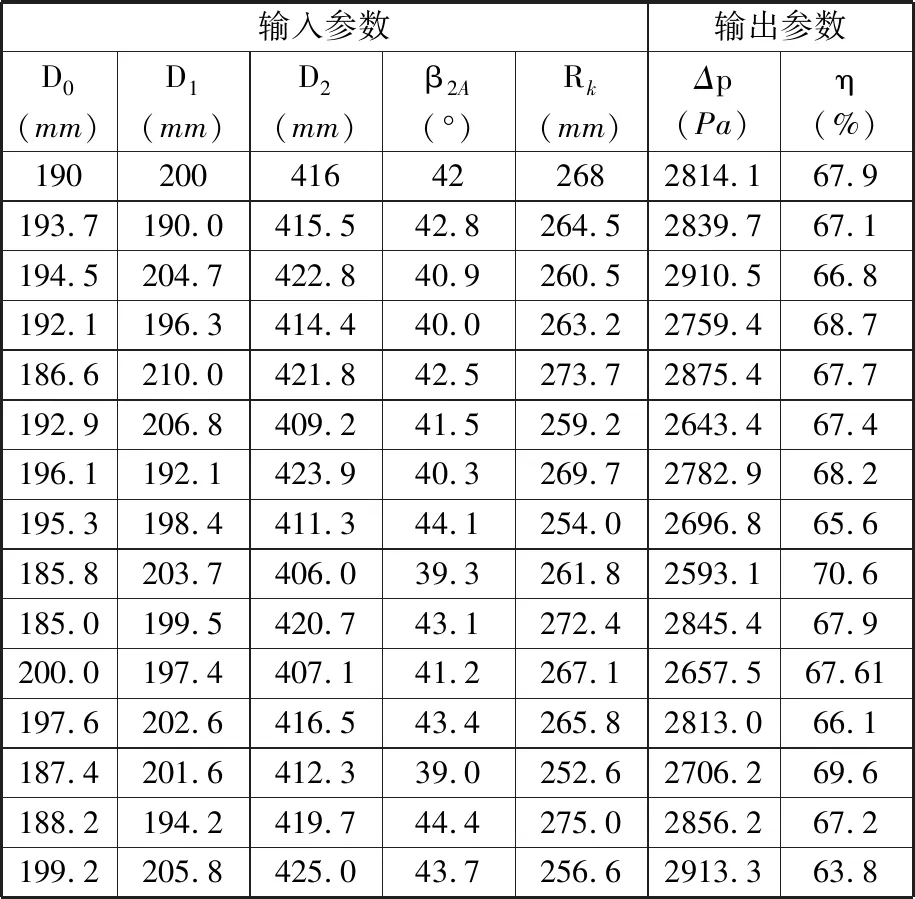
表4 LHS结果

RBFNN的输入层由叶轮进口直径D0、叶片进口直径D1、叶轮外径D2、叶片出口安装角β2A和叶片的圆弧半径Rk构成;输出层为全压Δp和效率η。输出的模型误差分别为13.39%和3.42%。模型形状参数为1.5。模型缩放的矩阵如下:

采用全局灵敏性分析识别得到离心风机气动性能相关性分析结果,如图9所示。

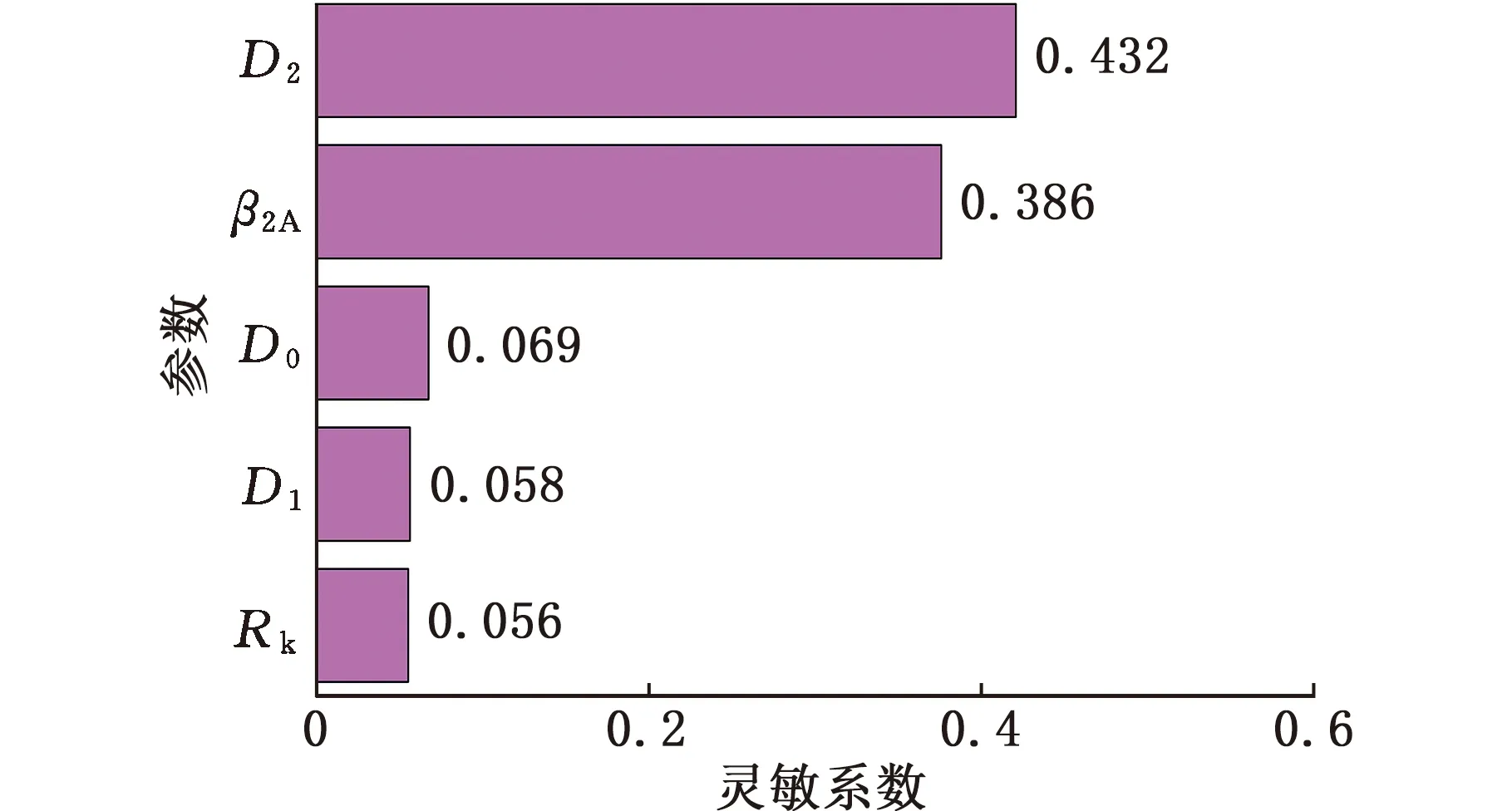
(a)全压

由图9可知,叶轮进口直径D0、叶轮外径D2和叶片出口安装角β2A对离心风机气动性能影响最大。其中,显著影响全压Δp的参数为叶轮外径D2和叶片出口安装角β2A,灵敏系数分别为0.432和0.386;叶片出口安装角β2A对效率η的影响最大,灵敏系数为0.541。

根据上述图9的全局灵敏性分析结果,对影响离心风机气动性能的叶轮结构参数D0、D2和β2A进行进一步的分析,如图10所示。可知,叶轮进口直径D0增大时,离心风机全压Δp先增大后减小,效率η逐渐减小。叶轮外径D2增大时,离心风机全压Δp逐渐增大,效率η逐渐减小。叶片出口安装角β2A增大时,离心风机全压Δp逐渐增大,在β2A=43°时出现拐点,然后减小,效率η逐渐减小。

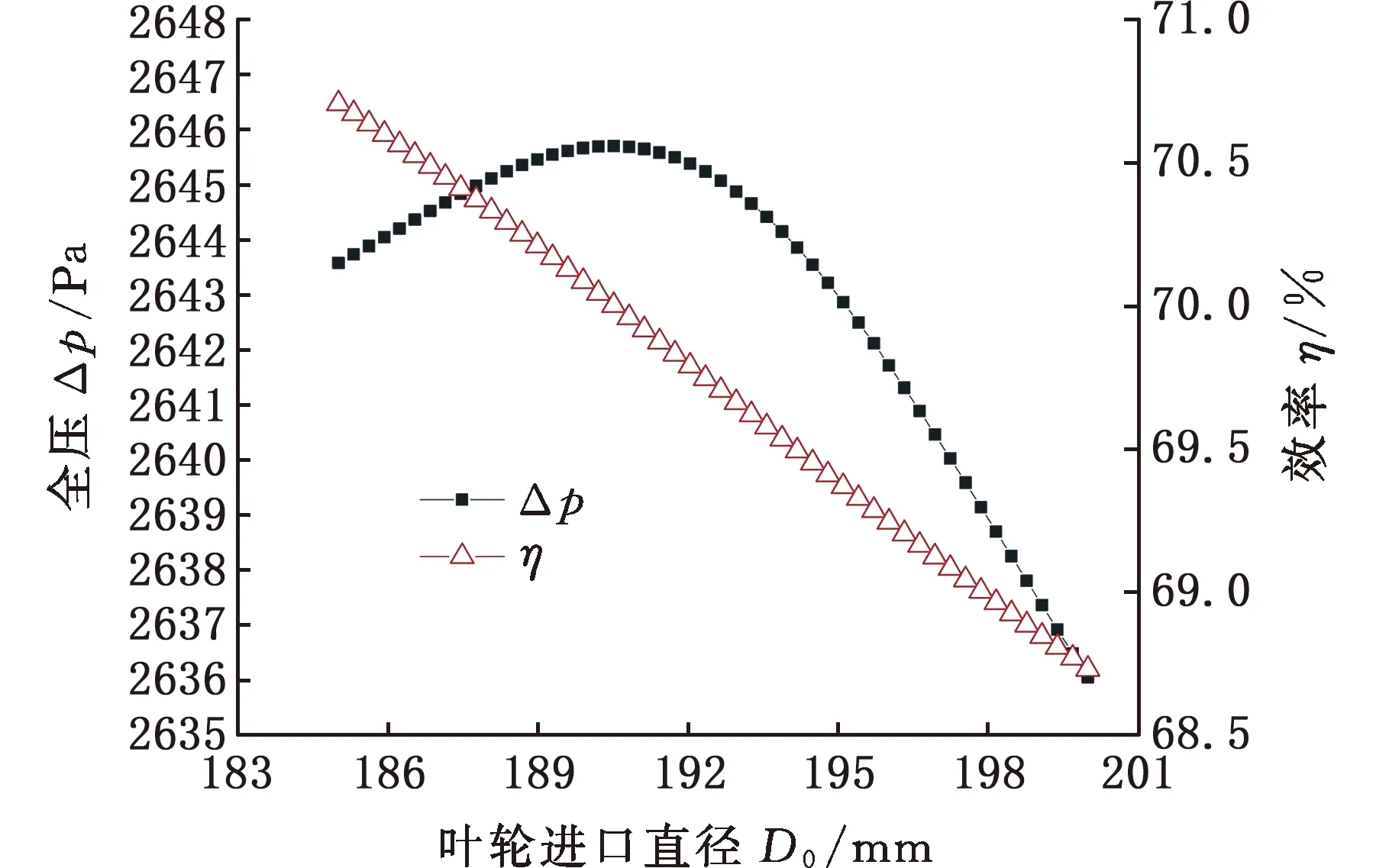
(a)叶轮进口直径D0

4 气动性能优化设计结果

根据上述研究,综合考虑各参数的影响,结合实际工程及工艺的要求,提出离心风机气动性能优化设计方案,如表5所示。

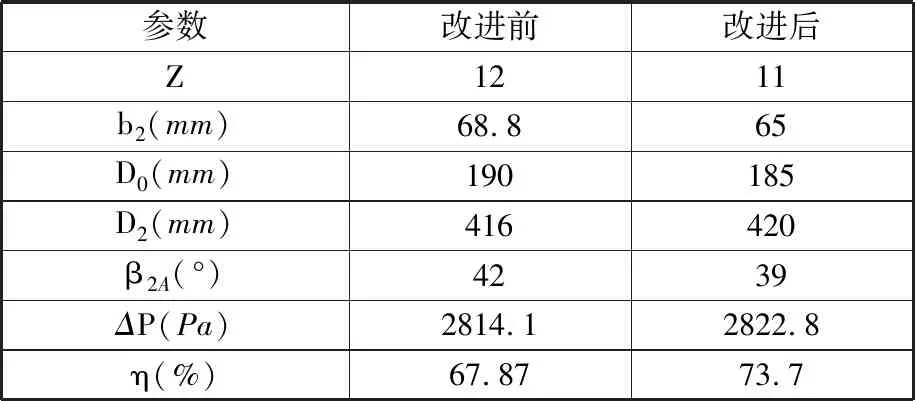
表5 改进前后的参数对比

分析改进后的离心风机工况点的流场,如图11所示。相对图6所示的原始方案流场,图11中叶轮速度分布图中的低速区和涡流现象明显得到改善,气流损失明显减小。

图12给出了改进前后的气动性能仿真计算结果的比较。由图12a可知,改进前后,离心风机离心风机工况点的效率η明显提高。风机在小于工况点的流量下,改进后方案的全压Δp值工况点的全压Δp值相当。由图12b可知,改进前后,大于原方案的全压Δp值;而在大于工况点的流量下,改进后方案的全压Δp值小于原方案的全压Δp值。在客户给定风机全压Δp=2625 Pa工况下,风机的流量可达到0.73 m/s。根据实际工况,风机工作的流量通常小于工况点,因此可以满足实际工程要求。

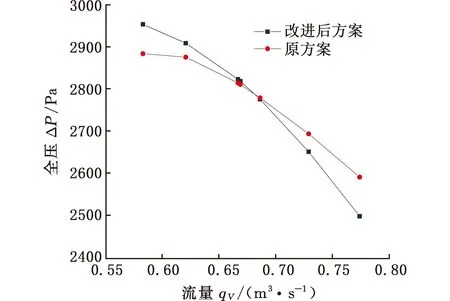
(a)全压ΔP与流量qV的关系

5 结论

(1)针对叶片数Z对离心风机气动性能影响进行单因素灵敏性分析,发现:全压Δp随叶片数Z的增加而增大,但当叶片数达到11及以上时,全压的变化不大;效率η随叶片数的增大呈先增大后减小,叶片数为11时的离心风机效率最高。因此,叶片数为11时,离心风机气动性能可达到最佳匹配。

(2)针对叶轮宽度对离心风机气动性能影响进行单因素灵敏性分析,发现:叶轮宽度为67 mm时离心风机全压最大;叶轮宽度为65 mm时效率最高。

(3)针对离心叶轮结构参数对离心风机气动性能影响进行多因素灵敏性分析,发现:叶轮进口直径增大时,全压先增大后减小,效率逐渐减小;叶轮外径增大时,全压逐渐增大,效率逐渐减小;叶片出口安装角增大时,全压逐渐增大,效率逐渐减小。

(4)通过优化改进叶片数、叶轮宽度、叶轮进口直径、叶轮外径和叶片出口安装角的数值,合理匹配叶轮结构参数,提出了改进优化离心风机气动性能的方案,工况点的效率由67.2%提高至73.7%,减小了气流损失,显著提高了风机效率。

气动噪声是目前列车车载风机面临的一大问题。下一步将对风机的性能和噪声进行联合研究,在满足性能要求的前提下,优化控制风机气动噪声。