分布式多柔性装配作业车间调度问题研究
魏光艳 叶春明
上海理工大学管理学院,上海,200093
0 引言
在经济全球化的背景下,为应对快速变化的市场环境,大量制造企业由单一工厂生产转变为多工厂生产,因此, 分布式工厂调度问题逐渐成为工业界和学术界的关注焦点。这种对多个制造单元进行调度决策的需求,催生了分布式调度的相关研究[1]。借助于智能生产系统,分布式制造可以实现对资源的统一配置,促进分散制造资源的组合优化与共享[2],因此,研究分布式车间调度问题具有重要的现实意义和应用价值。
分布式作业车间调度问题是作业车间调度问题的扩展,通常包括两个子调度问题:工件在加工工厂之间的分配,以及对工序的操作顺序进行排序[3-5]。由于柔性制造系统在分布式制造工厂中的普遍应用,分布式柔性作业车间调度问题(distributed and flexible job-shop scheduling problem, DFJSP)引起了广泛关注。MENG等[6]提出了四种混合规划模型和一种约束规划模型用于求解DFJSP,以最小化最大完工时间为优化目标,在不同规模的DFJSP上进行了有效性验证。吴秀丽等[7]构建了以总成本和提前/延期为优化目标的双目标DFJSP模型,并利用改进的差分进化算法进行求解。LI等[8]以最小化最大完工时间、最大工作负载、总负载和提前/延误为优化目标,构建了多目标DFJSP模型,并设计了混合禁忌搜索算法用于求解模型。其他一些学者在DFJSP的基础上,考虑了一些更加复杂的约束,以使模型更适合实际生产环境,例如王凌等[9]、DU等[10]、张洪亮等[11]研究了考虑运输时间的分布式绿色柔性作业车间的调度问题,并分别利用协同群智能算法、混合分布估计算法、改进的遗传算法对模型进行求解;XU等[12]考虑部分工件的操作需要外包的情况,构建了多目标DFJSP模型,并将遗传算法和禁忌搜索算法相结合对模型进行求解;LUO等[13]同时考虑了运输时间和允许工件操作外包的情况,构建了多目标DFJSP模型,并提出了一种模因算法用于求解模型;郭晨等[14]以最小化生产成本和拖期时间为目标,建立了分布式装配柔性模糊车间调度模型,并利用混合分布估计算法进行求解。还有一些学者结合实际生产案例对DFJSP进行了研究,例如TANG等[15]以砂型铸造作业车间为例,构建了以最小化最大完工时间为目标的DFJSP模型,通过试验证明了所提出的混合教学优化算法的有效性;SANG等[16]基于分布式智能工厂生产系统,构建了多目标DFJSP模型,并提出了一种模因算法用于求解模型,最后利用机床部件生产厂的生产信息进行了试验。
以上学者针对DFJSP以及带运输时间或允许工序外包的DFJSP模型进行了研究,提高了模型的实用性。文献[15-16]则分别基于砂型铸造作业车间和机床部件生产厂的调度需求,对具体案例进行了建模和求解。然而,该类研究仅考虑了调度过程中的机器柔性,而在集装配和加工一体化的分布式多柔性装配作业车间调度问题(distributed and multi-flexible assembly job-shop scheduling problem, DMFAJSP)中,还需要考虑工人安排柔性和工序顺序柔性[17-19]。
目前已有一些研究,在调度过程中考虑了工序顺序柔性[20]和工人安排柔性。例如,胡瑞淇等[21]基于表达式树结构建立了考虑工序顺序柔性的作业车间调度问题(flexible job-shop scheduling problem, FJSP)模型,设计了一种工序顺序的随机生成方式,并以遗传算法为例设计了求解流程;ZHANG等[22]研究了考虑工艺顺序柔性的FJSP,构建了带装配的FJSP模型,并利用分布式蚁群算法进行求解;董海等[23]构建了具有机器、工人和工序多柔性的FJSP模型,并设计了离散回溯搜索算法进行求解;VITAL-SOTO等[24]利用有向无环图表示工序的操作优先级,建立了具有排序柔性的双资源约束FJSP模型,提出了带有创新算子的精英非支配排序遗传算法用于求解模型。
这些研究提供了工序顺序柔性的表示方式,为构建DMFAJSP模型提供了参考。然而,上述考虑工序顺序柔性和工人安排柔性的调度研究都限定在单个柔性作业车间范围内,缺乏对分布式多柔性制造系统的调度研究。因此,本文将对考虑工序顺序柔性、工人安排柔性和机器选择柔性的DMFAJSP进行研究。
DMFAJSP需要对四个子调度问题进行决策,包括将工件分配给工厂、为工序执行顺序排序、为工序安排操作工人和为工序选择机器。由于DMFAJSP的调度过程和可行解的结构较为复杂,本文将采用模因算法(memetic algorithm, MA)进行求解,该算法可以同时进行全局搜索和局部搜索。
目前已有一些学者基于遗传算法如NSGA-Ⅱ[13,25-26]、NSGA-Ⅲ[16]等,结合各类局部搜索算子设计了模因算法,并通过大量试验证明了模因算法在求解DFJSP问题上具有良好的性能。与遗传算法通过交叉变异等操作产生种群的方法不同,分布估计算法(estimation of distribution algorithm, EDA)通过空间采样和统计学习,预测未来的搜索空间[27-28],从而利用概率模型解决多维调度问题。EDA算法具有显著的全局搜索优势,但同时存在局部搜索能力较弱和易收敛早熟的缺点[14]。而模因算法通过将基于种群的全局搜索和基于个体的局部搜索相结合,可以有效提高算法的寻优能力[29]。
因此,本文尝试根据DMFAJSP的特点,提出一种以分布估计算法作为全局搜索组件,以一些邻域搜索算子作为局部搜索组件的多维模因算法(multi-dimensional memetic algorithm, MDMA)。通过与其他算法进行对比试验,验证所提算法在求解DMFAJSP模型上的有效性。
1 DMFAJSP问题及模型
1.1 具有工序顺序柔性的作业车间调度问题
工件的工序顺序柔性分为图1所示的5种柔性等级[17],可以看出:当图1c中每个优先级中只有一道工序时,与图1a情况相同;当图1c中只存在一种优先级时,与图1b情况相同;而图1d和图1e则可以看作图1c的组合与变形。因此本文以图1c工序顺序非完全确定性工件为代表,研究考虑该类工序顺序柔性的DMFAJSP。

(a)工序顺序完全确定
1.2 分布式多柔性装配作业车间调度问题
在分布式多柔性装配作业车间的环境中,装配和加工过程被统一作为工序进行调度。DMFAJSP具有地理分布式、多柔性以及集加工和装配一体化的特点,除了上述提到的工序顺序柔性外,本文还考虑了工人安排柔性和机器选择柔性。该问题中有F个柔性工厂U,每个工厂Uf(f=1,2,…,F)中有Wf名工人,每名工人均会操作多台机器,Uf中的机器数量为Mf,每一台机器均具有多种加工功能。假设该问题中有N个工件J需要处理,工件Jn的工序有Rn个优先级,工件Jn中优先级为r的工序O有Knr个。其中,同一工件的工序若具有同样的优先级,则工序加工无次序要求;否则,低优先级的工序需在所有高优先级的工序加工完成后才可以进行加工。在DMFAJSP中,工序由不同的工人和机器组合进行加工时,加工时间可能不同。
1.3 相关假设
本文以最小化最大完工时间和总能耗为优化目标,相关的假设如下:
(1)每个工件只能由一个工厂进行加工;
(2)属于同一工件的工序,加工顺序受优先级约束,不同工件间的工序无优先级约束;
(3)每个工人均会操作多台机器,每台机器均可以加工多道工序;
(4)一个工人同一时刻只能操作一台机器,一台机器同一时刻只能加工一道工序;
(5)工序加工不可中断,直至该工序加工结束。
1.4 符号定义
DMFAJSP模型的数学描述中使用的符号及其含义如表1所示。
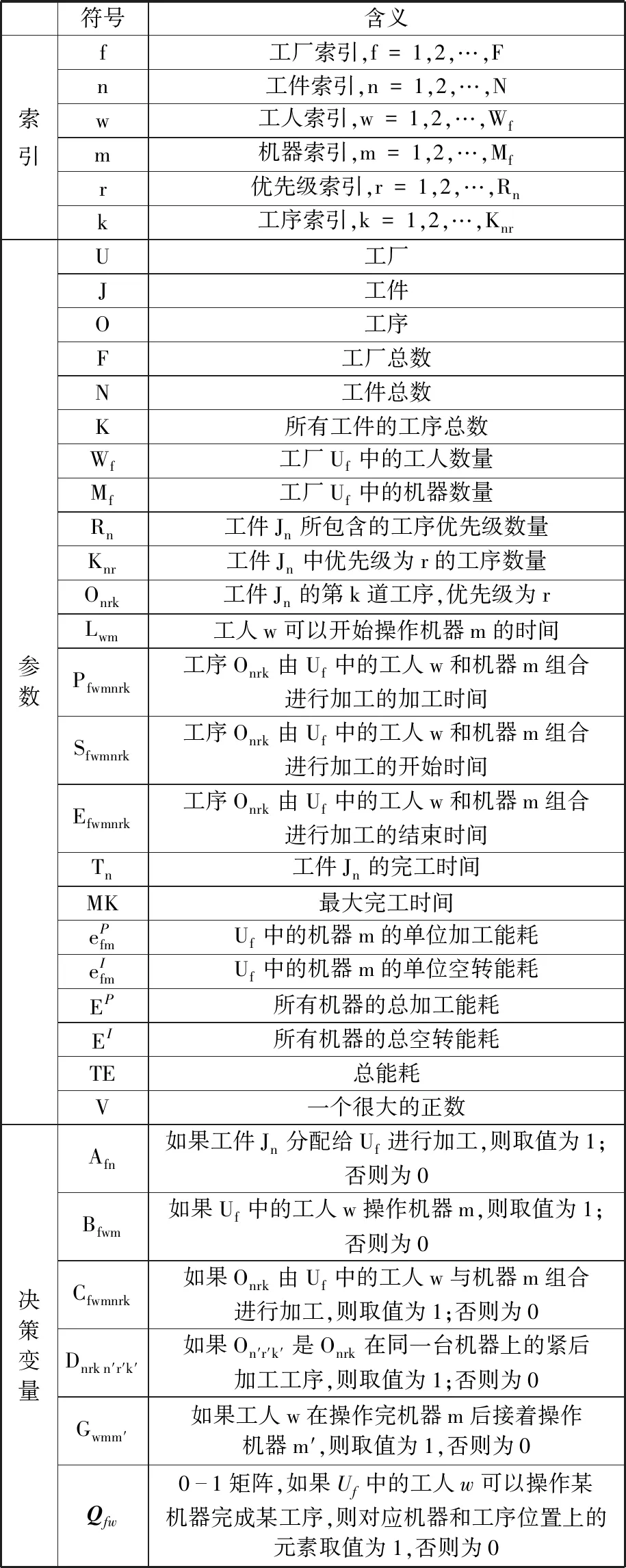
表1 符号表
1.5 数学模型
目标函数:
minMK=max(Tn) ∀n
(1)
minTE=EP+EI
(2)
其中,
(3)
∀f,w,m,n
(4)
∀w,n,r,k
(5)
∀w,n,r,k
式(1)和式(2)为目标函数,式(1)表示最小化最大完工时间,其中Tn的计算方式如式(3)所示;式(2)表示最小化总能耗,为所有机器的加工能耗和空转能耗的总和,所有机器的总加工能耗的计算如式(4)所示,总空转能耗的计算如式(5)所示。
约束条件:
(6)
(7)
(8)
(9)
(10)
Efwmnrk=Sfwmnrk+Pfwmnrk∀f,w,m,n,r,k
(11)
Sfwmnrk≥max(Efwmn(r-1)k|k=1,2,…,knr)
(12)
∀f,w,m,n,r∈[2,Rn]
Lwm′-Lwm≥V·(Gwmm′-1) ∀w,m,m′
(13)
Efwmn′r′k′-Efwmnrk≥Pfwmn′r′k′+V·(Dnrkn′r′k′-1)
(14)
∀f,w,m,n,r,k
(Sfwmnrk-Lwm)·Cfwmnrk≥0
(15)
(16)
(17)
约束条件中式(6)和式(7)表示每个工件只能分配给一个工厂,每个工厂可以分配到0至N个工件;式(8)表示工人为多能工,均会操作多台机器;式(9)表示每台机器都可以处理多道工序;式(10)保证每道工序只由一名工人操作一台机器加工;式(11)保证工序加工不中断,直到该工序结束;式(12)表示属于同一工件的工序,需在所有高优先级的工序加工完成后,才可以进行低优先级工序的加工;式(13)和式(14)表示同一时刻,每名工人只能操作一台机器,每台机器只能加工一道工序;式(15)表示每道工序只有在约定工人空闲时才可以开始加工;式(16)表示每名工人只能操作其会操作的机器且机器只能加工其可以加工的工序;式(17)保证所有工件的工序总数为所有工件中各优先级所包含的工序数量的总和。
1.6 问题案例
为了更好地理解DMFAJSP,以2个柔性工厂的生产环境为例{U1:[[w1,w2],[m1,m2,m3]],U2:[[w1,w2],[m1,m2]]},每个工厂各有2名操作工人以及分别有3台和2台机器,有3个工件{J1:[[2],[2],[1]],J2:[[1],[3],[1]],J3:[[1],[2],[2],[1]]}待分配,其中工件J1的工序具有3个优先级,每个优先级中分别有2道、2道和1道工序,其他工件的优先级和工序数量的表示方法与J1类似。工厂U1中工人W1所对应的Q11矩阵如表2所示,其他工人对应的Q矩阵与Q11类似。该案例在U1和U2中的一种调度安排结果如图2所示。
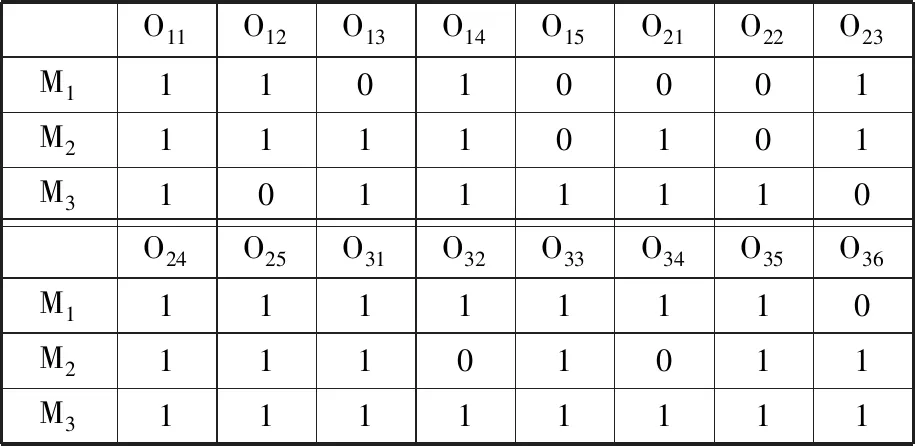
表2 案例问题中U1的Q表
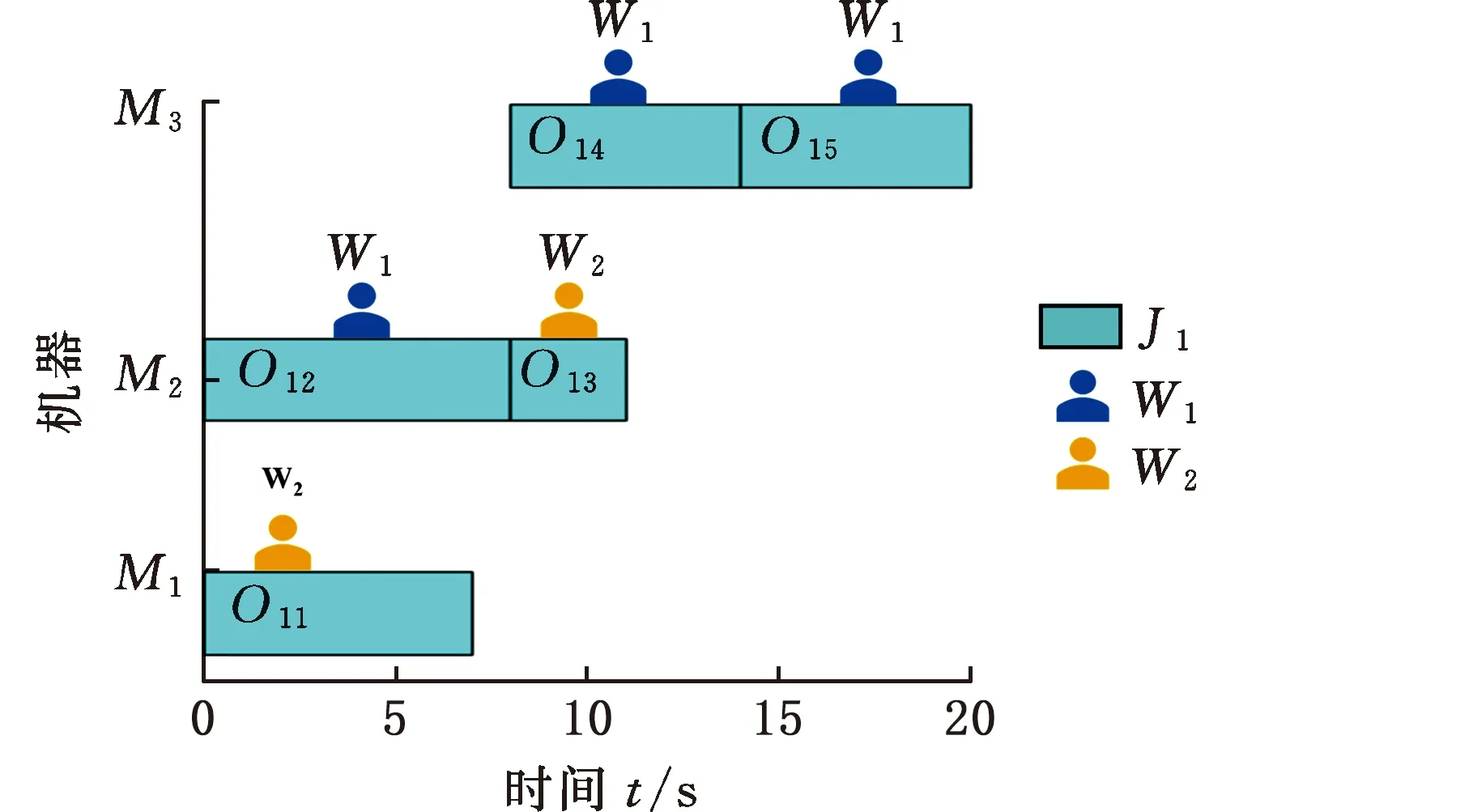
(a)U1
2 应用MDMA算法求解DMFAJSP
本文针对DMFAJSP可行解的多维特点构建了MDMA算法,该算法综合运用全局搜索和局部搜索进行寻优。其中全局搜索组件以分布估计算法为核心,局部搜索组件包括3种邻域搜索算子。
2.1 编码与解码
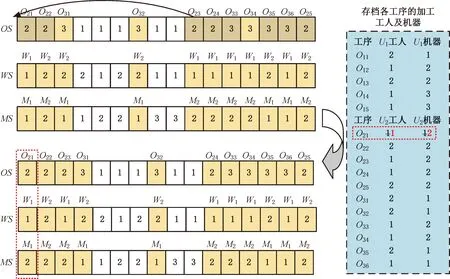
由于DMFAJSP问题可以根据需求将其分解为四个子问题:为工件分配工厂,为工序加工顺序排序,为工序分配加工工人以及为工序选择加工机器,因此,本文设计了多维编码方案来表示DMFAJSP模型的可行解。如图3中的编码图所示,每个解包含4个变量,各变量的释义如下:
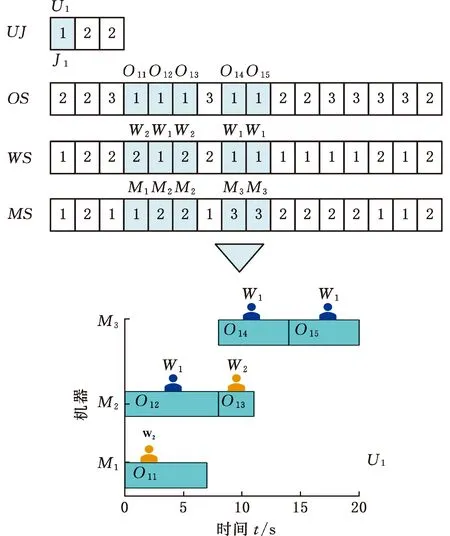
图3 编码与解码
UJ表示工件-工厂的分配方案,该变量中的数字代表工厂编号,位置索引表示工件编号;
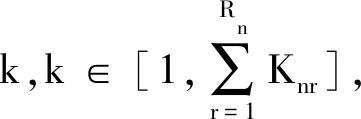
WS表示工人序列,该变量中的数字代表工人编号,工人编号的排列顺序与OS对应,即WS某位置上的工人将被安排加工OS对应位置上的工序;
MS表示机器序列,该变量中的数字代表机器编号,机器编号的排列顺序与OS和WS对应,即MS某位置上的机器被安排由WS中对应位置上的工人操作,一起加工OS中对应位置的工序;
图3中的甘特图展示了编码示意图中各变量彩色代码的解码结果,即工件J1的各工序在U1中被工厂内的工人和机器加工的调度安排。
2.2 概率模型
EDA算法中的概率模型用于描述候选解的分布信息,在迭代过程中通过对精英解和前代概率矩阵的统计学习完成概率矩阵的更新,从而实现解的进化。本文根据DMFAJSP的多维编码方案,构建了概率模型UJM、OSM和WMM对应的概率矩阵MUJM、MOSM、MWMM用于抽样生成种群。
2.2.1概率模型的构建
MUJM是工件-工厂分配概率矩阵,其元素unf表示第n个工件Jn分配到第f个工厂Uf进行加工的概率。MUJM在第0代的初始状态为
(18)
第g次迭代过程中的更新方式为
(19)
(20)
∀n,f,z∈[1,μ·P]
其中,α为学习率;μ为每代种群的精英选择率,本文设置为0.2;P为种群。
MOSM是工序序列概率矩阵,其元素sni表示工件Jn的工序出现在第i个位置上的概率,其中i∈[1,K]。MOSM的初始状态为
(21)
在迭代过程中的更新方式为
(22)
∀n,i
(23)
∀n,i,z∈[1,P]
其中,β为学习率。
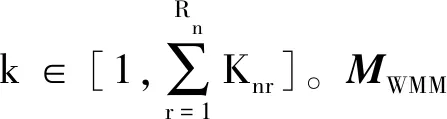
(24)
∀f,w,m,n,k
在迭代过程中的更新方式为
(25)
∀f,w,m,n,k
yfwmnk(g)=(1-γ)·yfwmnk(g-1)+γ·ρ
(26)
∀f,w,m,i
(27)
(28)
其中,γ为学习率。
2.2.2概率模型的通用性证明
为保证概率模型的通用性,需确保以下条件成立:
本文利用数学归纳法给出与条件(1)、(2)和(3)相关的模型通用性证明,如引理1、引理2和引理3所示。
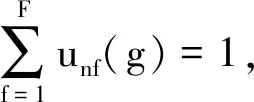
证明:当g= 0 时,有
(29)

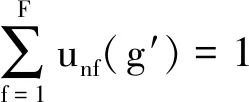
(30)
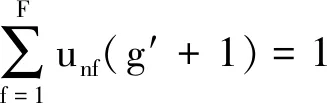
证明成立。
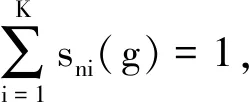
证明:当g=0时,有
(31)
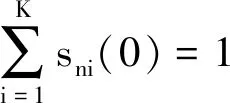
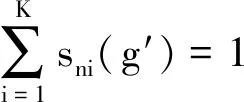
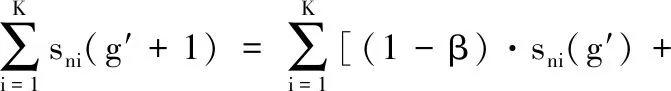
(32)
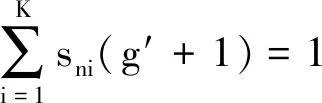

证明:当g= 0时,有
(33)
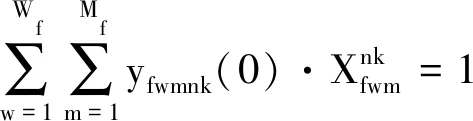
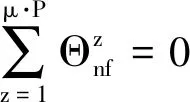
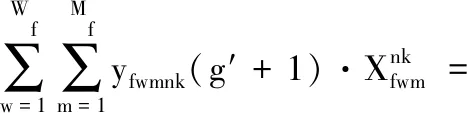
(34)
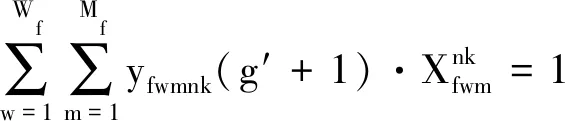
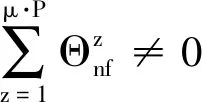
(35)
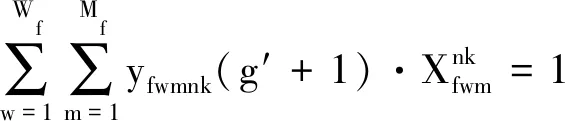
2.3 种群
2.3.1初始化种群
初始化种群采用全局生成方式、局部生成方式和随机生成方式,按照6∶3∶1的比例[9,13]生成。
全局生成方式:将工件分配给加工其所有工序总用时最少的工厂。
局部生成方式:为工件随机分配一个工厂,然后在该工厂为每道工序选择可用的且用时最少的工人和机器组合进行加工。
随机生成方式:将工件随机分配给一个工厂,并为每一道工序随机安排加工机器和操作工人。
2.3.2抽样生成种群
在迭代过程中,通过采样2.2节中的概率模型生成UJ、OS、WS和MS变量组成新的个体。为方便操作,分别对UJM、OSM和WMM模型的概率矩阵MUJM、MOSM和MWMM中的元素进行累加,形成辅助矩阵MUJSM、MOSSM和MWMSM。第g代辅助矩阵中的元素u′nf(g)、s′ni(g)和y′fwmnk(g)如下所示:
(36)
(37)
(38)
在一次迭代过程中,利用辅助矩阵生成变量UJ、OS、WS和MS的过程如算法1、算法2和算法3所示。
算法1抽样生成UJ
输入:MUJSM
输出:UJ
01: forn←1 toNdo
02:θ1←random(0,1)
03: forf←1 toFdo
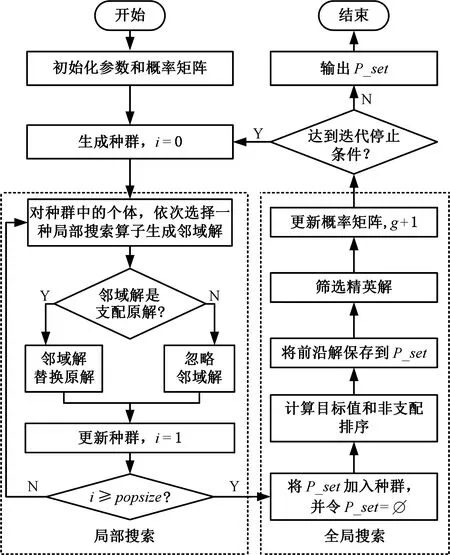
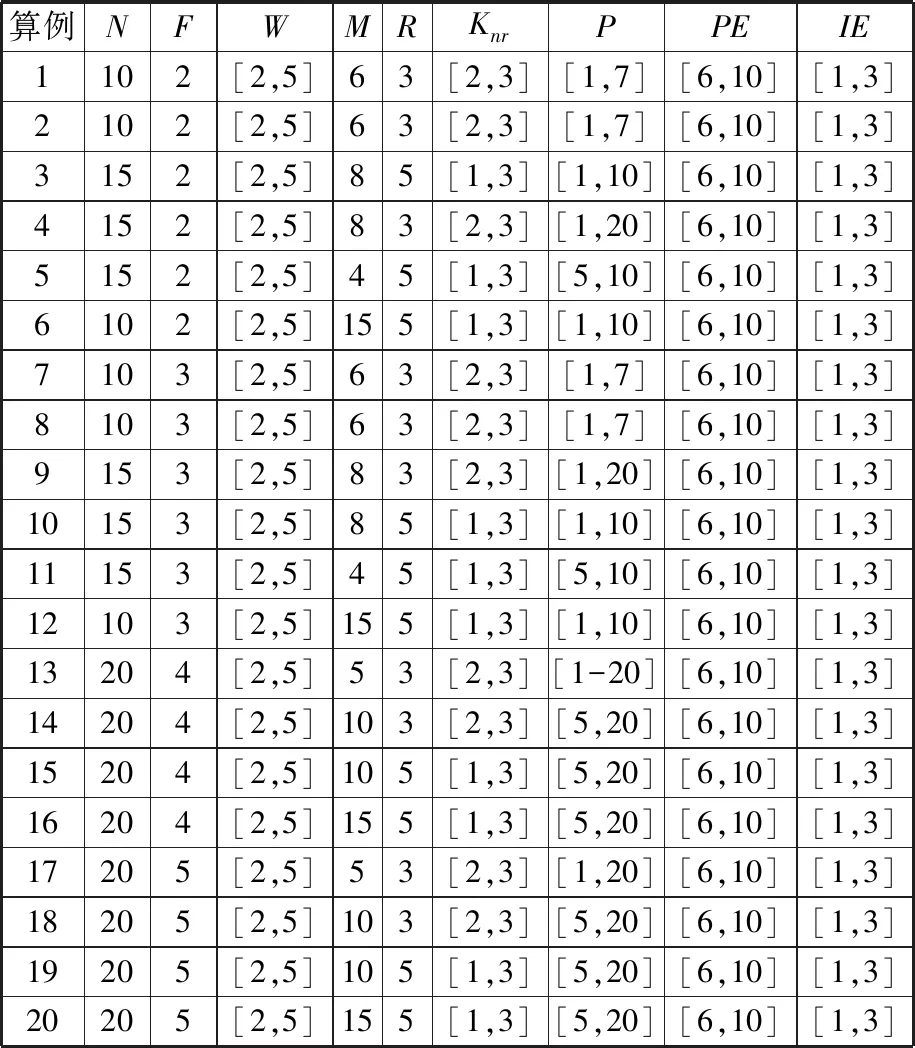
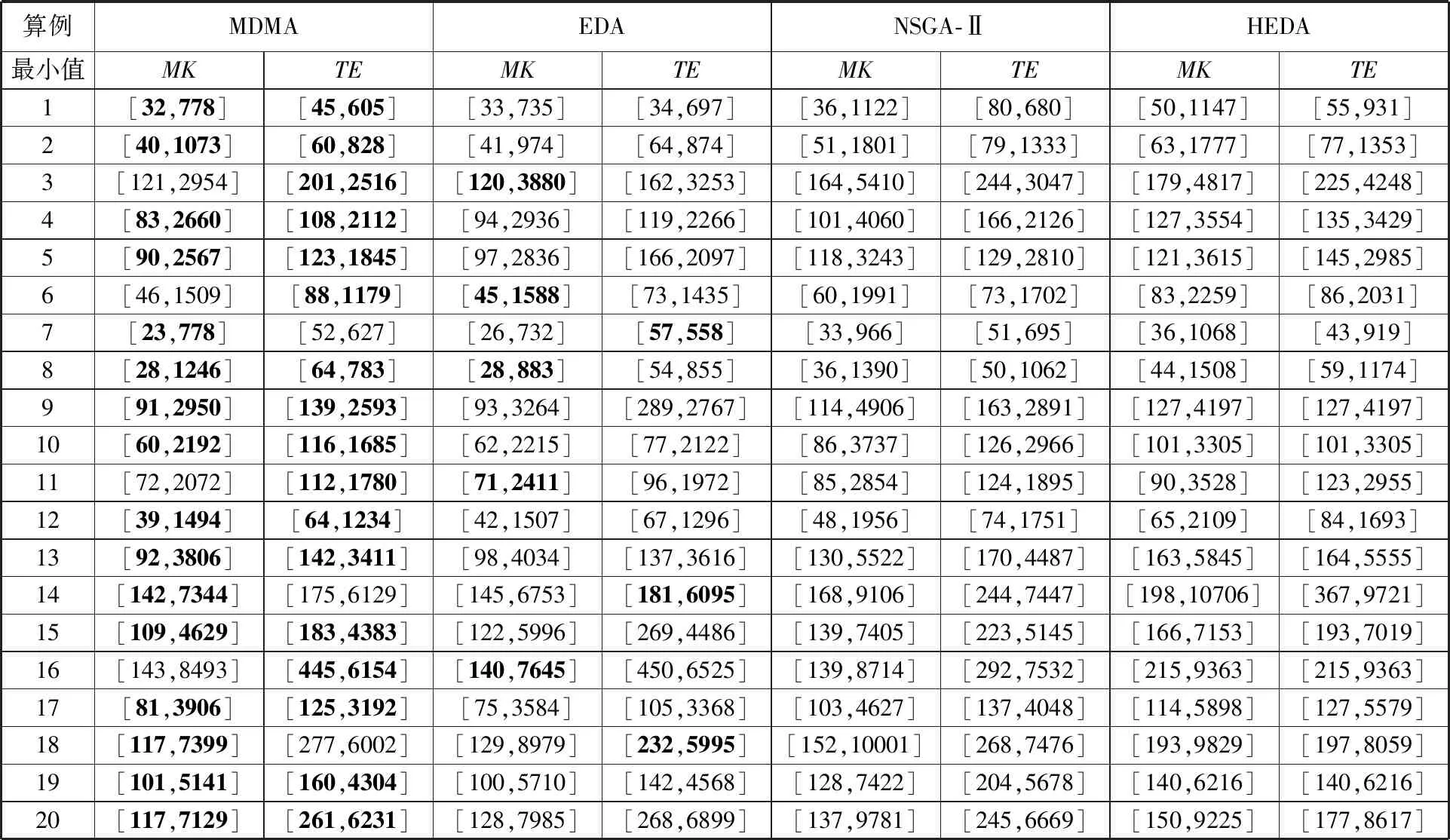
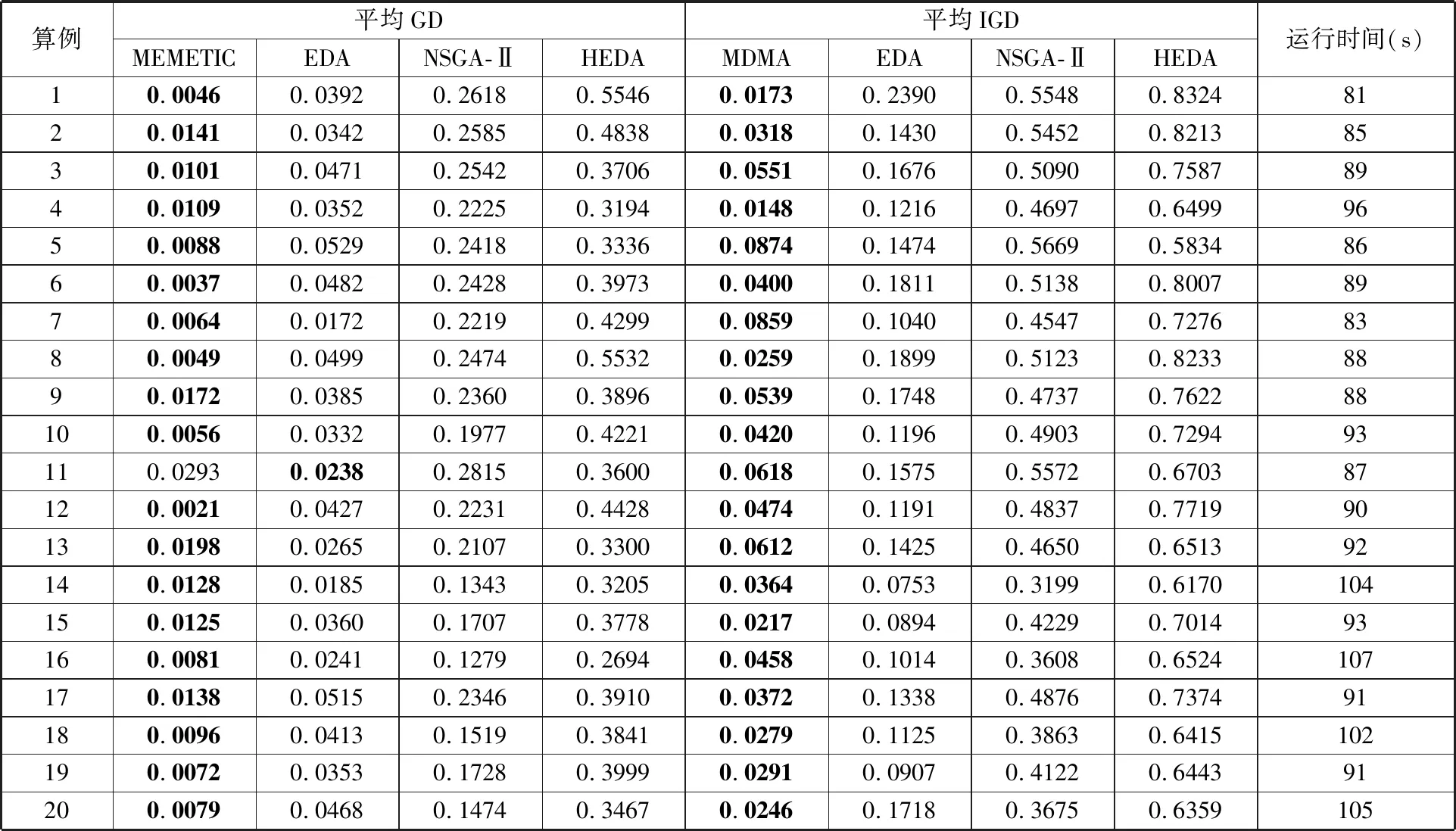
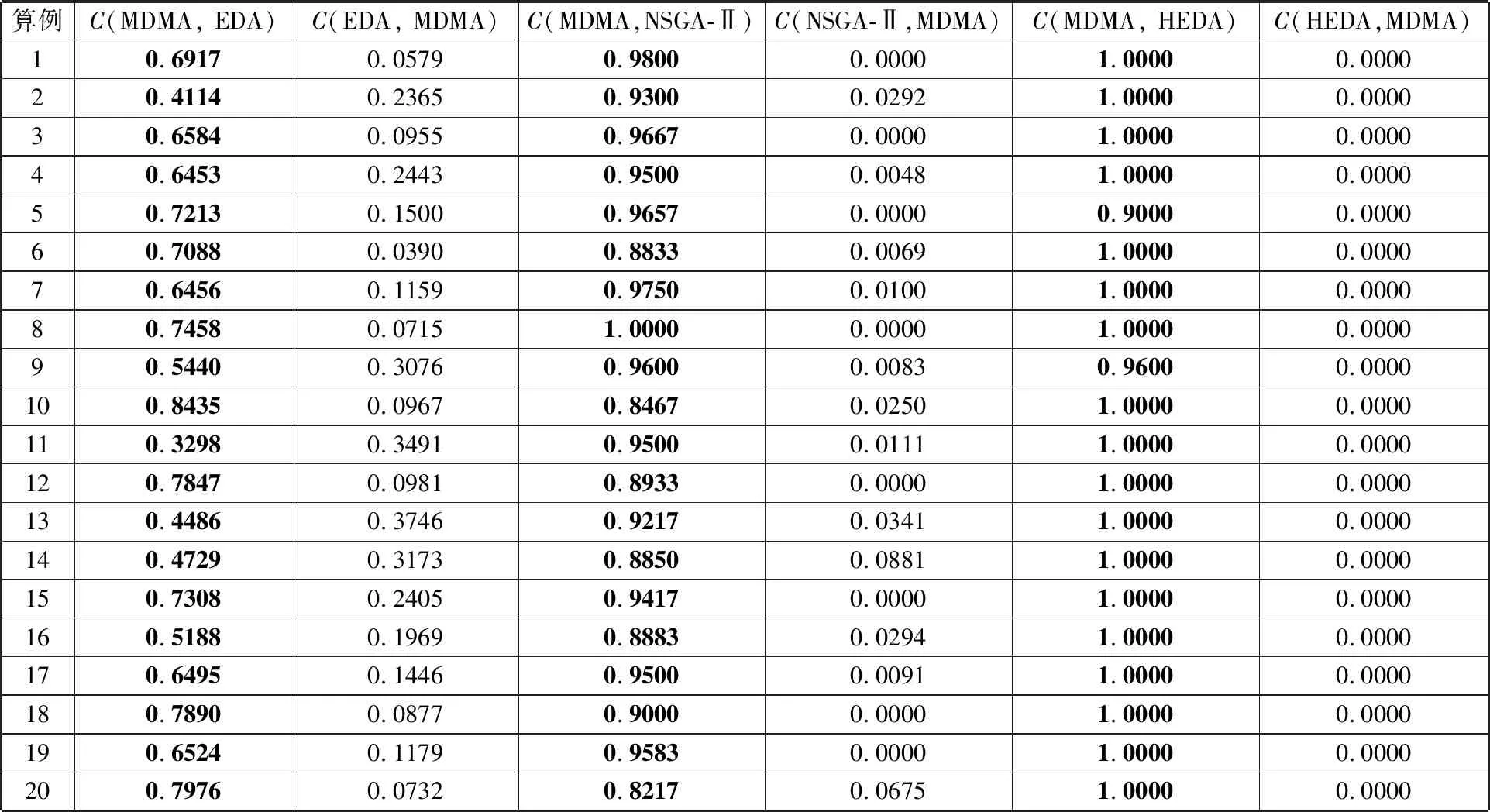
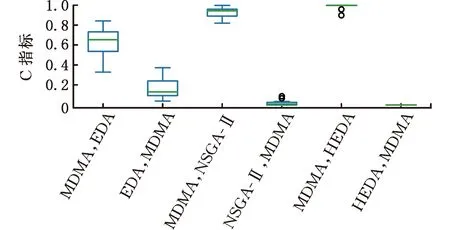
04: ifθ1 05:UJ[n]←f 06: end if 07: end for 08: end for 算法2抽样生成OS 输入:MOSSM 输出:OS,OK 01: forn←1 toNdo 03:θ2←random(0,1) 04: fori←1 toKdo 05: ifθ2 06:OS[i]←n 07:OK[i]←k 08: forj←1 toNdo 09:ossni← 0 10: end for 11: end if 12: end for 13: end for 14: end for 算法3抽样生成WM 输入:UJ,OS,OK,MWMSM 输出:WM 01: fori←1 toKdo 02:n←OS[i] 03:f←UJ[n] 04:k←OK[i] 05:θ3←random(0,1) 06: forw←1 toWfdo 07: form←1 toMfdo 08: ifθ3 09:MS[i]←m 10:WS[i]←w 11: end if 12: break 13: end for 14: end for 15: end for 本文设计了3种邻域结构NS1、NS2、NS3,以提高种群多样性和收敛速度。邻域结构的性能取决于邻域结构的连通性和规模[30],只有对关键路径上的工序进行操作才有可能减少最大完工时间[31]。因此,本文针对UJ变量设计了邻域结构Ⅰ,并基于关键路径构建了针对OS、WS和MS变量的邻域结构Ⅱ和Ⅲ。具体操作如下所示: (1)邻域结构Ⅰ。选择完工时间最晚工厂,将其中最后完工的工件分配给最早完工的工厂。工序序列保持不变,将原工厂中为该工件工序分配的工人和机器编号剔除,并在新工厂中随机为该工件的工序安排工人和机器。 (2)邻域结构Ⅱ。如图4所示,首先,对原个体中的变量对应关系进行存档。然后,在关键路径(OS变量中填充阴影的工序)中随机选择一个关键工序,将其移动到头关键工序之前(或尾关键工序之后),并为移动后的工序选择加工时间最小的工人和机器。其他工序的加工工人和机器依照之前存档的对应信息保持不变。 图4 邻域结构Ⅱ示意图 (3)邻域结构Ⅲ。首先,对原个体中的变量对应关系存档。然后,在关键路径上随机选择一个与头关键工序(或尾关键工序)不属于同一工件的工序,并将该工序与头关键工序(或尾关键工序)进行位置交换。所有工序对应的加工工人和机器与存档中的对应信息保持一致。 本文设计的MDMA框架如图5所示。首先,根据2.3.1节中的初始化种群策略生成初始种群。接着,对初始化种群进行局部搜索,根据贪心策略保留初始个体或其邻域解。然后进行全局搜索,按照2.2.2节中描述的方法通过快速非支配排序和拥挤距离筛选精英解。根据2.3.2节的方法,利用新的概率模型抽样生成新一代种群。再对新种群循环进行局部搜索和全局搜索,直到达到迭代停止条件,输出最终的帕累托前沿解。 图5 MDMA框架 本文试验采用python3编程语言进行编写,运行环境为Intel Core i7, 3.6 GHz,4×8 GB RAM。为验证MDMA在求解DMFAJSP方面的有效性,将MDMA与EDA、NSGA-Ⅱ[32]和HEDA(hybrid estimation of distribution algorithm)[14]进行对比试验。本文算例为基于BRANDIMARTE[33]提出的MK01-10算例,扩展形成的20个试验算例,如表3所示。 表3 试验算例 MDMA需要确定的参数包括:种群规模popsize、精英选择率μ和3个概率模型的学习率α、β、γ。通过田口试验[34]确定参数的最优组合,其中每个因素设置4个水平,并采用L16(45)正交表进行试验设计。测试算例为表3中的算例10,迭代停止时间设置为100 s,每组参数组合独立运行10次。参数试验的评价指标选用多目标偏差和(objectives deviation sum, ODS)[13],其计算方法如下所示: (39) i=1,2,…,9n=1,2,…,in 其中,in为算法基于参数组合i得到的前沿解总数量;bjn为第n个前沿解第j个目标的值。参数组合及10次运行的平均ODS如表4所示,参数水平趋势如图6a所示,根据参数水平趋势确定MDMA的最优参数组合为:α=0.5,β=0.3,γ=0.4,μ=0.2,popsize=150。 表4 MDMA算法参数组合及平均ODS (a)MDMA 此外,为保证对比算法的公平性,对比算法的最优参数组合同样采用田口试验设计方法进行设置。对比算法的参数及水平如表5所示,其中NSGA-Ⅱ的参数cr为交换率,mu为变异率;HEDA中的f为缩放因子。基于对比算法的参数数量,分别采用L16(45)、L9(33)、L16(44)正交表进行参数组合试验。各算法的参数水平趋势如图6所示,EDA的最优参数组合为:α=0.5,β=0.2,γ=0.4,μ=0.2,popsize=50;NSGA-Ⅱ的最优参数组合为:popsize=50,cr=0.6,mu=0.1;HEDA的最优参数组合为:α=0.4,f=0.2,cr=0.2,popsize=150。 表5 对比算法参数水平 为测试所提算法MDMA对求解DMFAJSP模型的性能,本文将MDMA与EDA、NSGA-Ⅱ和HEDA进行对比。其中EDA算法为不包含局部搜索算子的MDMA,因此通过对比MDMA与EDA,可以验证MDMA中局部搜索算子的有效性。所有算法的初始种群生成方式一致。所有算法在每个算例上独立运行10次。由于NSGA-Ⅱ是解决车间调度类问题最为经典的算法之一,为保证试验公平,对于每个算例,所有算法的运行时间统一设定为NSGA-Ⅱ迭代100次所需的时间。 对比试验的评价指标选择常见的世代距离(generational distance, GD)、反转世代距离(inverted generational distance, IGD)和解集覆盖率(coverage,C)指标,各指标的计算公式如下: (40) (41) (42) 试验结果如表6~表8和图7所示。其中,表6展示了对比试验中每个算法在每个算例上运行10次得到的最小MK、TE的非支配解。对比试验的平均GD、IGD指标结果和每个算例的运行时间如表7所示,C指标如表8所示。此外,利用箱形图展示了对比算法C指标的分布情况,如图7所示。 表6 对比试验最小单目标值的非支配解 表7 对比试验的平均GD和平均IGD 表8 对比试验的C指标 图7 C指标箱线图 表6中第1列表示算例编号,第2列表示MDMA算法在每个算例上10次运行结果中得到的最小MK对应的非支配解,第3列表示其得到的最小TE对应的非支配解,后续4~9列分别表示EDA、NSGA-Ⅱ和HEDA获得的最小MK和TE对应的非支配解。从表6中可以看出,MDMA在75%的算例上取得的MK最小值优于其他算法,且在85%的算例上取得的TE最小值优于其他算法。由表7可以看出,除了算例11,MDMA的GD和 IGD指标均优于EDA,说明MDMA求得的解在收敛性和多样性方面均优于EDA。结合表8和图7中C(MDMA,EDA)、C(EDA,MDMA)指标及分散情况,MDMA获得的非支配解占比均高于EDA,可以验证MDMA中局部搜索算子可以显著提高MDMA的解的质量。另外,从表7、表8和图7中可以看出MDMA的GD、IGD和C指标均优于NSGA-Ⅱ和HEDA,说明MDMA算法所求得的解在收敛性、多样性以及非支配解占比方面均优于NSGA-Ⅱ和HEDA求得的解。验证了MDMA算法在求解DMFAJSP问题上具有明显优势。 本文针对分布式多柔性装配作业车间的调度问题,构建了以最小化最大完工时间和最小化总能耗为优化目标的数学模型。该模型考虑了调度过程中存在的机器选择柔性、工人安排柔性和工序顺序柔性。为了求解该模型,本文提出了一种多维模因算法(MDMA)。首先,根据调度模型的特点,设计了多维编码方案,用于表示问题模型的可行解。随后,在MDMA算法的全局搜索阶段,根据编码方案设计了3种概率模型,用于抽样生成种群。并且,为了验证概率模型的通用性,采用数学归纳法进行了推理和证明。在MDMA的局部搜索阶段,设计了3种邻域结构,其中有2种邻域结构基于关键路径进行设计,以有效提高算法的局部搜索效率。最后,在20个分布式多柔性装配作业车间调度问题(DMFAJSP)算例上,将所提算法与分布估计算法、遗传算法和混合分布估计算法进行了对比。结果验证了所提MDMA算法对于求解DMFAJSP问题具有显著优势。 此外,本文在研究分布式多柔性装配作业车间的调度问题时,仅考虑了静态的调度过程。后续将对更复杂的动态DMFAJSP模型进行研究。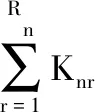
2.4 局部搜索算子
2.5 算法框架
3 试验与分析
3.1 参数设置
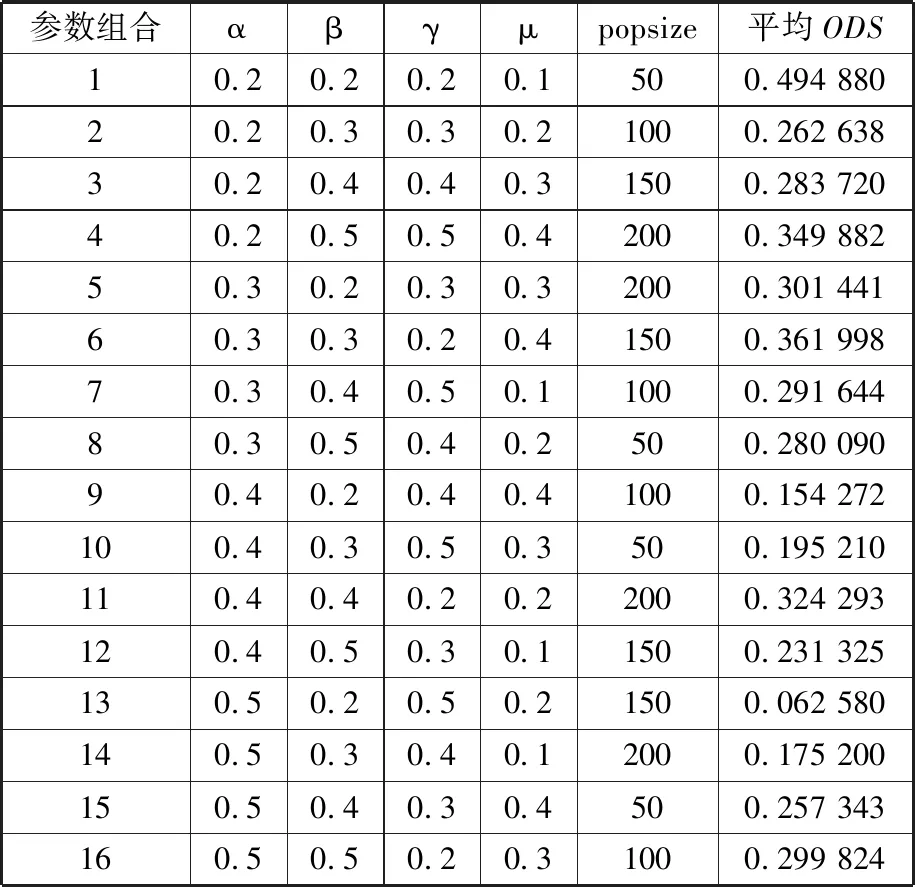
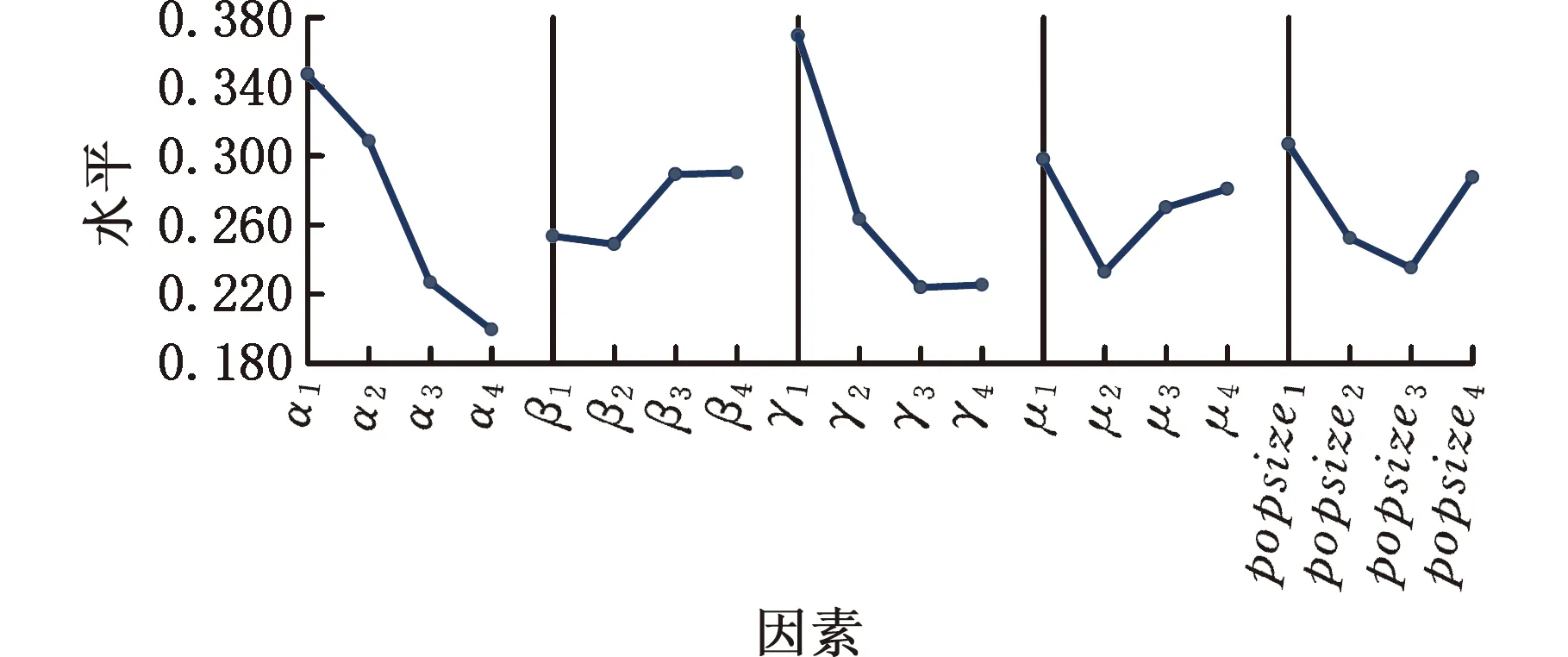
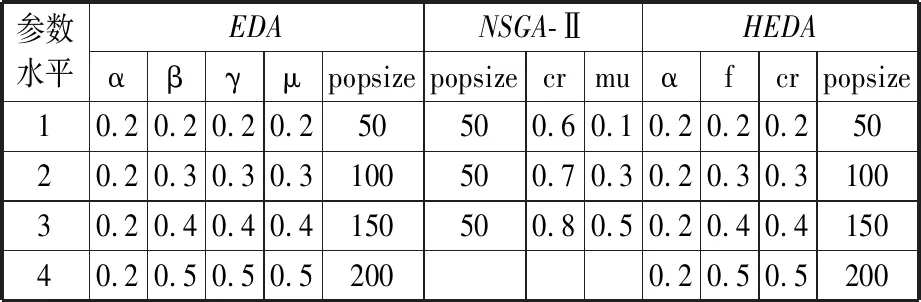
3.2 对比试验及结果分析
4 结语

